以任意结点为根的准二叉树自动布局算法设计

姜学东 孙海民

(河北民族师范学院 数学与计算机科学学院，河北 承德 067000）

以任意结点为根的准二叉树自动布局算法设计

姜学东 孙海民

(河北民族师范学院 数学与计算机科学学院，河北 承德 067000）

在开发数据结构学习软件时，用户提出这样的需求：任意次以任意结点为根实现准二叉树结点的自动布局。通过分析发现，对准二叉树进行图的广度优先遍历算法是解决问题的关键。首先将准二叉树看作图建立邻接表，然后对其进行广度优先遍历，建立准二叉树的三叉链表和自动布局链表，最后对二叉树进行先根遍历，根据三叉链表中结点的父子兄弟关系，计算自动布局链表中的结点位置，从而实现结点的自动布局。使用该软件变了学生对二叉树的习惯性感知，对理解二叉树的概念和有关遍历算法有着极大的促进作用。

数据结构；算法；二叉树；自动布局；三叉链表

1、引言

《数据结构》课程在计算机科学中占有十分重要的地位[1]。但学生学习该课程时往往感觉很困难。数据结构及其算法的教学难点在于它们的抽象性和动态性[2]。在学习或使用数据结构及其程序设计时学习效果差、程序开发低效等现象普遍存在，造成这种现象的一个很主要的原因在于没有实现数据结构可视化，在程序设计过程中不能直观形象地显现所建立的数据结构[3]。为此，人们开发数据结构软件以帮助学生对课程中算法的理解。

在开发二叉树数据算法演示学习软件时，为了帮助学习者深入理解二叉树各种算法，我们没有在软件中预设二叉树，而是由学生使用该软件自己创建二叉树，他们可以根据自己知识经验进行数据建模，二叉树结点的数量、位置和模型复杂程度由学生自己设定。软件中对二叉树的数据建模规则设计如下：

1.1 鼠标双击界面创建二叉树结点。

1.2 鼠标单击结点后，拖动鼠标到另一个结点内，则创建边。

1.3 每条边必须与两个结点相连。不存在没有结点相连，或者只有一个结点相连的边。

1.4 用户可以创建任意多个结点，但与每个结点相连的边不超过3条，没有边与之相连的结点，称为游离结点。

1.5 用户数据建模时不规定根结点及结点的父子关系，数据建模完成后，由用户指定某个结点为根结点，但不指定子结点的父子兄弟关系，数据建模如图1所示。

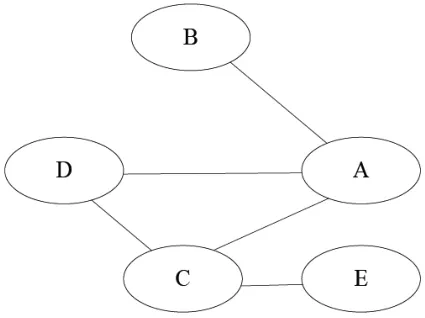
图1 准二叉树

由于二叉树的结点数量、位置和模型复杂程度由学生自己设计，所以数据建模结果可能是二叉树，也可能不是；同时，模型中没有确定结点的父子兄弟关系，因此称之为准二叉树。

2、需求分析

对于一颗准二叉树图1所示，用户在进行算法演示时如先根遍历，则需要明确根结点是哪个结点，该软件在数据建模完成后，并没有指定根结点。二叉树的根结点是由学生任意指定的，A、B、C、D、E都可以指定为根结点。该软件之所以这样设计的目的之一，是要打破学习者的思维定势，改变他们认为根节点总是在顶端或者底端位置的希望习惯。目的之二是，通对同一颗准二叉树，以不同结点为根，进行算法演示能够加深学生对算法的理解，拓展他们的思维空间。因此，我们提出该软件能够对一颗准二叉树任意次以任意结点为根，实现结点自动布局。为达到这个目的软件必须实现如下功能：

2.1 对用户的数据建模结果进行有效性判断。用户选定根结点后，判断准二叉树是否为二叉树。如果不是二叉树则提示用户。

2.2 识别根结点，判断结点的父子兄弟关系，实现结点自动布局。不论数据建模中结点的布局如何，该软件总能够使得其以规则的形式分布。根结点处于最上方；同层的结点处于同一水平位置；不同层结点在垂直方向上等间距；子结点以父结点的中垂线为轴对称分布。如图2所示图1二叉树以“A”为根结点的自动布局。

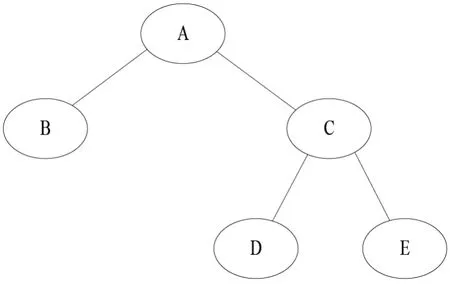
图2 以A为根结点自动布局

2.3 建一个数据结构来保存自动布局的二叉树。数据建模后，用户可以对该模型多次以任意结点为根，实现结点自动布局，所以不能修改用原来数据建模。如图3所示图1二叉树以“e”为根结点的自动布局。

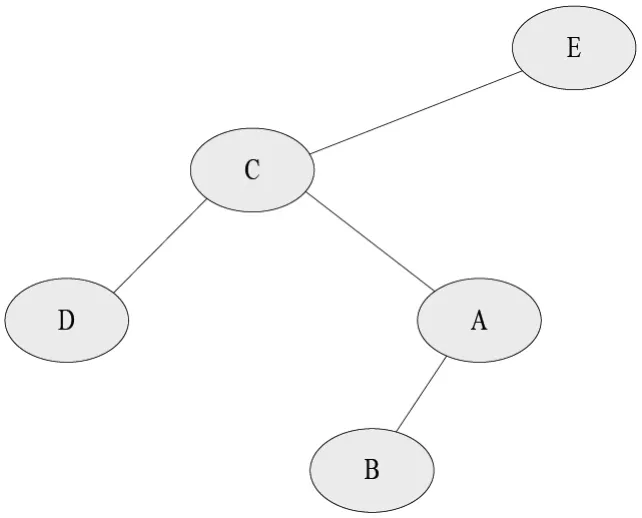
图3 以E为根结点自动布局

3、算法分析

3.1 建立三叉链表

准二叉树结点的自动布局以建立它的三叉链表为基础。根据规则，数据建模完成后，用户选择其中一个结点作为根，依据如下条件对准二叉树的有效性判断：

（1）与根相连的边数是否小于3？

（2）是否为连通？

（3）是否不存在回路？

如果满足这三个条件，表明这是一颗二叉树。先不考虑这三个判断，首先分析如果一颗准二叉树满足上述条件，怎样建立三叉链表并实现结点的自动化布局。根据规则，以用户选中的结点为根，通过根结点可以找到与之相连的边，通过边就可以找到另一端的结点，这个结点就是根的孩子，同理可以找到根的另一个孩子(如果有的话)。这样就得到二叉树的第二层结点。同样的方法找到第三层结点，第四层结点……这样就可以确定结点间的父子关系。然后，通过子结点之间的物理位置来确定子结点的兄弟关系（当为一个子结点时，通过父子间物理位置，来确定是左孩子还是右孩子）。这样就确定了这颗准二叉树每个结点的父子兄弟关系，也就可以建立它的三叉链表。

分析发现，这种方法实际是按照二叉树层次遍历来建立三叉链表。那么，使用怎样的算法对二叉树进行层次遍历？树是图的一种形式，对准二叉树的层次遍历就可以首先把它看作是图，建立邻接表。然后对它进行图的广度优先遍历，这样就得了到建立三叉链表的算法。

进一步分析，对准二叉树进行广度优先遍后，如果还存在没有被遍历的结点，则该准二叉树是非连通图。如果遍历过程中遇到遍历过的结点，那么该结点应该是邻接表中当前头结点的父结点。如果不是，则此准二叉树一定存在回路。至于对与根结点相连的边不能超过3条的判断是很容易的。这样就解决了对数据建模有效性的判断问题。

3.2 结点自动布局

在既定的条件下，视图高度和宽度都已确定，二叉树结点位置不应该超出这个范围。Windows GDI绘图时，默认映射模式MM_TEXT，其坐标原点为窗口左上角，水平轴向右递增，垂直轴向下递增[3]。假设视图有效画图高度为H，宽度为W。对准二叉树进行广度优先遍历后，可知该二叉树的深度N，则结点的水平位置：

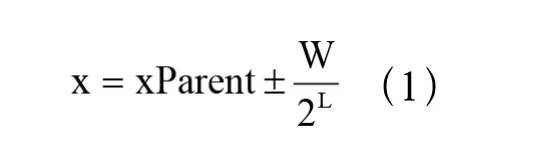
xParent父结点水平位置，L结点所处层数，正负符号取决于结点是左/右孩子。当为根结点时，xParent值为W。将视图高度平均N等分后，得到结点的垂直位置：

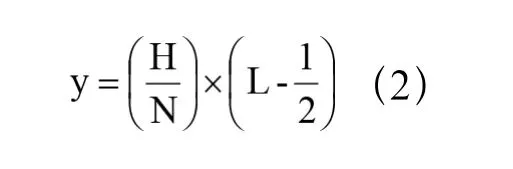
为避免子结点相互重叠必须设计结点的大小。二叉树最高层结点数量为2N-1个，所以结点最大宽度为W／2N-1，最大高度为H／N。在程序中可预设结点的宽度和高度，当预设结点宽度和高度超过实际计算值时，就使用实际值绘制结点，否则使用预设值绘图。

广度优先遍历后，根据二叉树深度，确定结点宽度和高度。然后再对该二叉树进行先根遍历，根据上面的公式设置结点位置，从而实现结点的自动布局。

3.3 自动布局链表

为实现对同一颗准二叉树能够任意次的，以不同结点为根进行自动化布局。必须再设计出一个用于结点自动布局的链表，并使之与数据建中的结点保持一一的对应关系。为便于在遍历中查找对应的结点，在建立自动布局链表结点、邻接表头结点和表结点时，要使它们与数据建模中结点的ID相等。自动布局链表的建立过程，如图3所示。

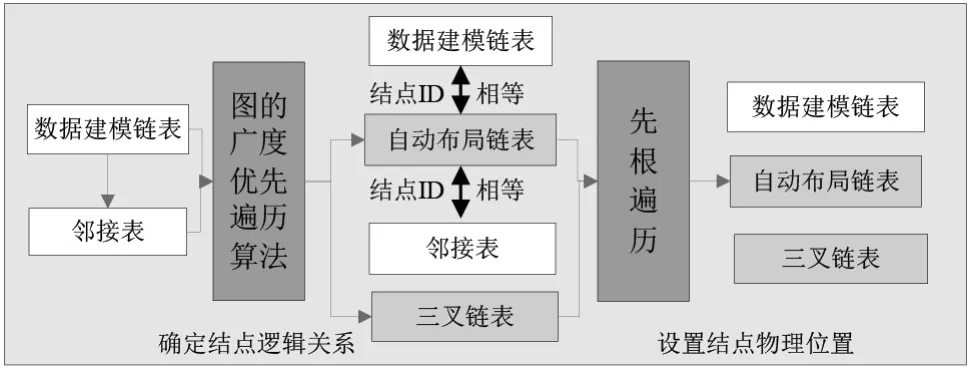
图4 自动布局链表的建立过程

4、算法实现的设计

该软件基于MFC类库开发，使用SDI文档视图结构作为开发框架。在程序中设计数据建模和结点自动布局两个界面，数据建模完成后，学生选中某个结点作为根结点，在右键菜单中添加自动布局命令。单该命令后，隐藏数据建模界面，显示结点自动布局界面。当关闭自动布局界面后，显示数据建模界面，学生可以选择另外一个结点创建二叉树结点自动布局。

4.1 数据结构设计

4.1.1 数据建模和自动布局链表

数据建模中结点和边都从基类派生；结点中有一个成员变量保存该结点的位置信息，有一个管理与此结点相连的边的数组；边中保存与之相连的两个结点；结点和边通过一个CObList类对象管理；每个结点都有唯一的ID。根据广度优先遍历的结点遍历顺序，依次创建自动布局结点，并使该结点数据与数据建模结点数据相同。在对二叉树进行先根遍历中，根据结点的父子兄弟关系，重新计算结点的位置。

4.1.2 邻接表

使用邻接表作二叉树的图的存储结构，设计表结点（CNode）、头结点（CHead）和邻接表（CGraph）三个类。在表结点和头结点类中包含成员m_iID作为结点的唯一标识，在广度优先遍历中使用该变量，查找相应的结点；包含m_bWisited变量作为该结点是否被遍历过的标记。在邻接表中使用HeadList链表来管理头结点，在头结点中使用NodeList链表来管理与之相连的表结点。

图5 邻接表类图

4.1.3 三叉链表结点类

设计三叉链表的结点类（CBTNode），其成员变量包括：层数、标识、左孩子、右孩子、父结点和一个指向自动布局链表结点(CBinaryTreeNode)的指针。通过该指针得到与三叉链表结点对应的自动布局链表中的结点。在该类中设计SetBinaryTreeNodePosition(CPoint posParent， BOOL bLeft)函数，实现计算自动布局链表中结点位置的功能。函数第一个参数是父结点在自动布局界面中的位置，第二个参数指出该结点是左孩子还是右孩子。

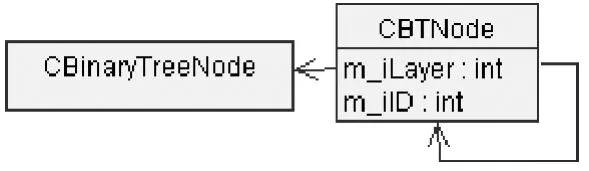
图6 三叉链表结点类

4.2 广度优先遍历算法

对准二叉树进行广度优先遍历[4]的算法如图4所示。图中有一个大循环——队，存储未被遍历的邻接表的头结点。在遍历中从队中取出队头，从头结点中得到表结点链表，从表结点链表中再取出表结点。如果此表结点没有被访问过，则将与表结点ID相等的头结点入队，继续循环。如果表结点已被访问，且不是当前头结点的父结点，则该二叉树中存在回路。当队为空时，遍历结束。遍历结束后，如果图中还存在没有被遍历的头结点，则准二叉树为非连通图。

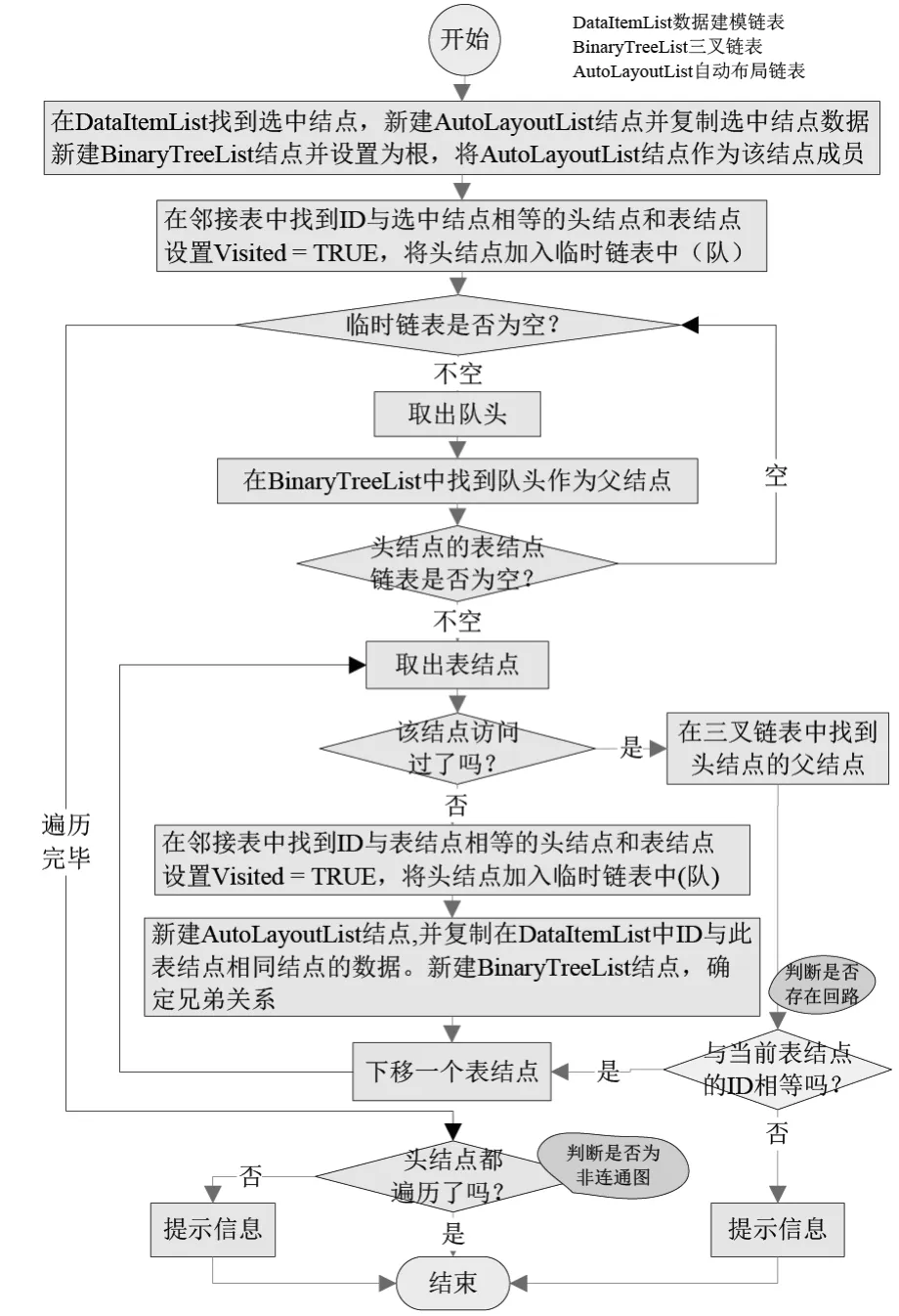
图7 准二叉树的广度优先遍历算法

在图4中，通过邻接表可以确定结点的父子关系。结点的兄弟关系通过如下方法确定。首先判断父结点是否已经存在左（右）孩子，如果存在则在数据建模链表中找到该结点，比较它们的位置确定兄弟关系；如果父结点没有孩子，则通过比较父子在数据建模链表中结点的位置，确定该结点是左/右孩子。

确定了二叉树结点的父子兄弟关系后，根据二叉树的深度，重新设计自动布局链表结点的大小。然后，再对二叉树进行先根遍历，根据前面得到的公式(1)(2)重新计算自动布局链表结点的位置。从而实现结点自动布局。

5、结论

该文改变了学生对二叉树习惯性感知，对理解二叉树的概念和有关遍历算法有着极大的促进作用。通过对准二叉树进行图的广度优先遍历，建立其三叉链表和自动布局链表。又通过对其先序遍历，计算自动布局链表的结点位置，从而实现结点的自动布局。

[1]熊岳山,陈怀义.《数据结构》教材改革的设想[J].高等教育研究学报,2000,(2):62.

[2]杨晓波.数据结构可视化CAI系统的设计与实现[J].计算机应用与软件,2008,(9):196.

[3]杨晓波,王聪华.COM组件技术在数据结构可视化中的应用[J].微计算机信息，2007,(6-3):233.

[4]Jeff Prosise.MFC Windows程序设计[M].北京博彦科技发展有限责任公司译.北京:清华大学出版社,2001.

[5]严蔚敏,吴伟民.数据结构[M].北京:清华大学出版社,1997.

On Laying Out a Quasi-Binary Tree Rooted on Any Node

JIANG Xue-dong; SUN Hai-min
(Network Information Center, Chengde Teachers’ College, Chengde, 067000, China)

How to lay out a quasi-binary tree rooted on any node automatically many times is the problem the author encountered in his software development. It’s critical to carry out the algorithm of breadth-first search on the quasi-binary tree. First, the quasi-binary tree is considered as a graph and adjacency list is created for it. Second, it is traversed by using the algorithm of breadth-first search. The trinary linked list and automatic layout linked list are created during the traversal. Finally, it is traversed by using the algorithm of preorder traversal. The position of the node of the automatic layout linked list is calculated by the relationship of parent-child and being brothers of the corresponding node in the trinary linked list. The software changes students' perception about the binary tree and promotes their understanding of the concepts and algorithms of it.

Data Structure; Algorithm; Binary tree; Laying out automatically; Trinary linked list

O1-8

A

2095-3763(2017)04-0121-06

10.16729/j.cnki.jhnun.2017.04.018

2017-08-24

姜学东（1980- ），男，黑龙江拜泉人，河北民族师范学院数学与计算机科学学院，讲师(实验师)，硕士，主要研究方向为计算机网络系统与计算机信息管理系统；孙海民（1970- ），男，河北承德人，满族，副教授，硕士研究生，主要研究方向为计算机网络系统与计算机教育应用。

2017年承德市科技局项目“承德市基于LBS的承德避暑山庄景区游客移动服务系统设计与开发”（编号：201702B008）；2017年河北省教育厅资助科研项目“Flattening特点的大学课程学习过程性评价系统研发”（编号：Z2017154）；2017年河北省科学技术研究与发展计划科普专项项目“智慧教育知识科普网建设” (编号17K50320D）；2015年度承德市教育科学研究“十二五”规划专项课题“承德高校翻转课堂实施路径研究”（编号：1501001）。

责任编辑：宋 爽