一个三角形不等式及其等价式与相关式

浙江省湖州市双林中学 李建潮 钱旭锋 (邮编：313012)

一个三角形不等式及其等价式与相关式

浙江省湖州市双林中学 李建潮 钱旭锋 (邮编：313012)

本文通过一个三角形不等式的确立,拟以此为母不等式探求其一系列的等价经典三角形不等式,并因势利导再次确立一系列的相关经典三角形不等式.

为叙述简洁起见,本文拟用 ∑ 表示循环和,例如：x＋y＋z＝∑x,yz＋zx＋xy＝∑yz等.并约定：在 △ABC中,内角A、B、C的对边依次为a、b、c,R、r依次为它的外接圆、内切圆半径.

1 一个三角形不等式

不难发现,在△ABC中成立着如下不等式：

定理 在△ABC中,有

(b－c)2cosA ＋ (c－a)2cosB ＋ (a －b)2cosC≥0 ①

证明 由对称性不妨设A≤B≤C,则a≤b≤c(c－a≥b－a＞0),且cosA＞0,cosB＞0.所以,(c－a)2cosB≥(b－a)2cosB.于是

①式左边≥(c－a)2cosB＋(a－b)2cosC

≥(a－b)2(cosB＋cosC)＝(a－b)2·2sin

定理获证.

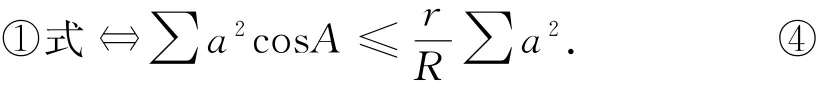
证明 ③式⇔∑a2(cosA＋cosB＋cosC)－ ∑a2cosA ≥ ∑a2⇔∑a2cosA ≤(∑cosA－1)∑a2

三角形恒等式：

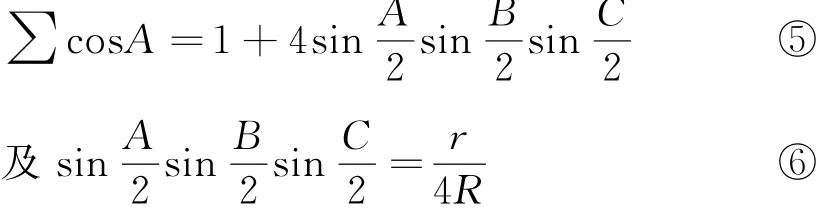
一并代入上式,有

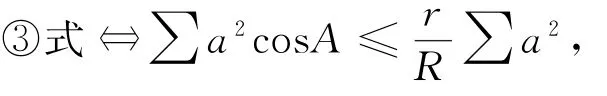
即定理与④式等价.又

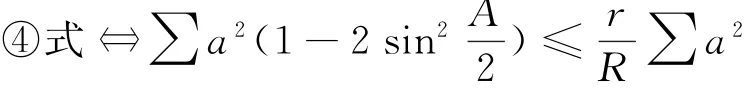
注 由余弦定理：a2＝b2＋c2－2bccosA,等三式易知定理实则是

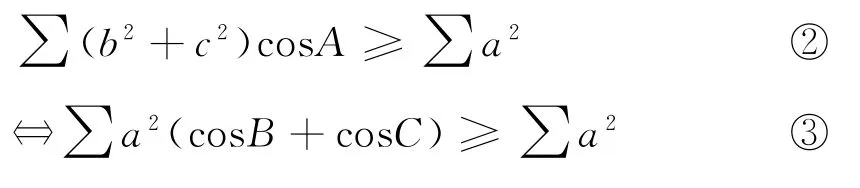
2 定理(即②、③式)的几个等价式

等价式1 在△ABC中,有

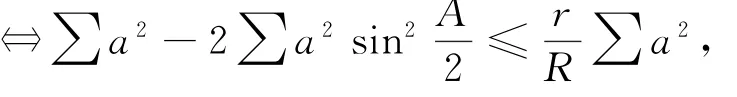
由此得

等价式2 在△ABC中,有

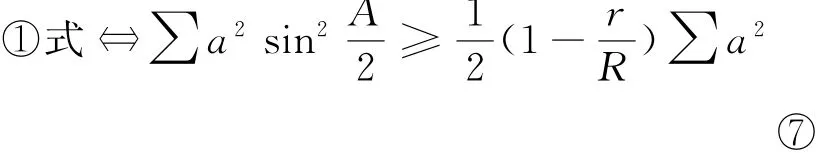
等价式3 在△ABC中,有

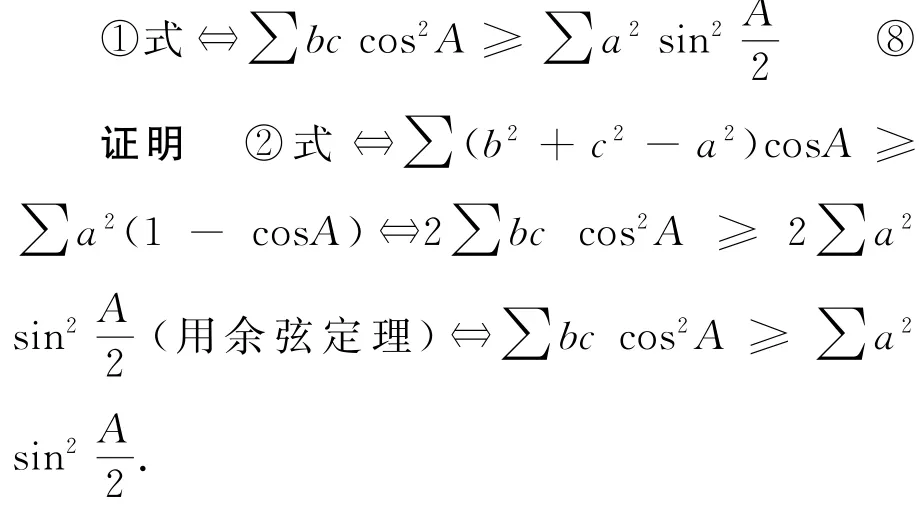
即定理与⑧式等价.

等价式4 在△ABC中,有

证明 在△ABC中,由正弦定理,有

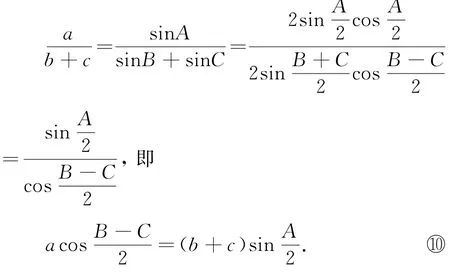
于是,有

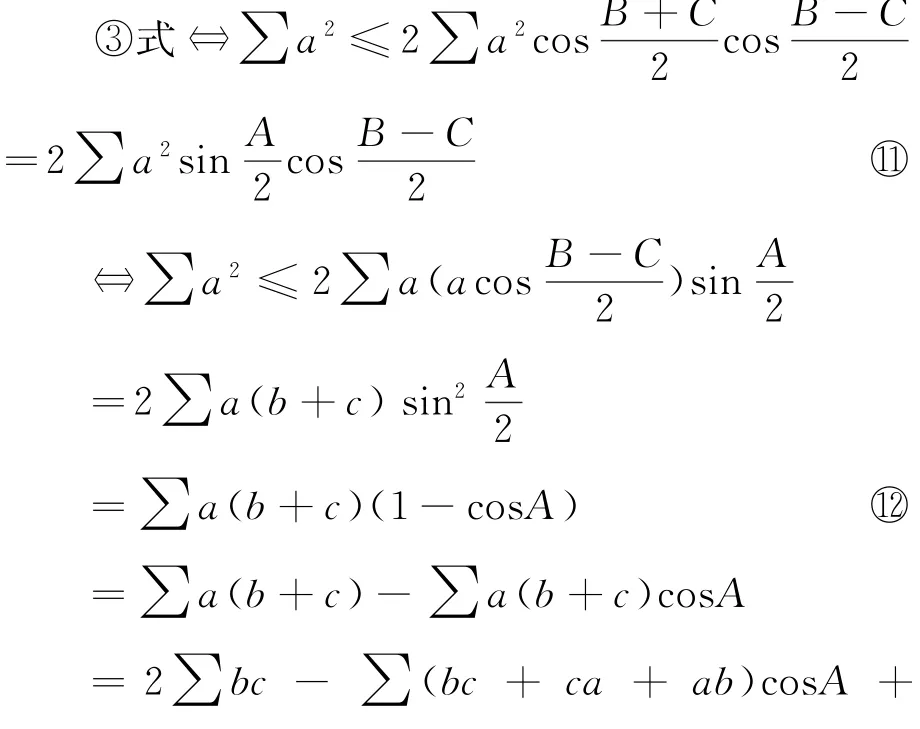
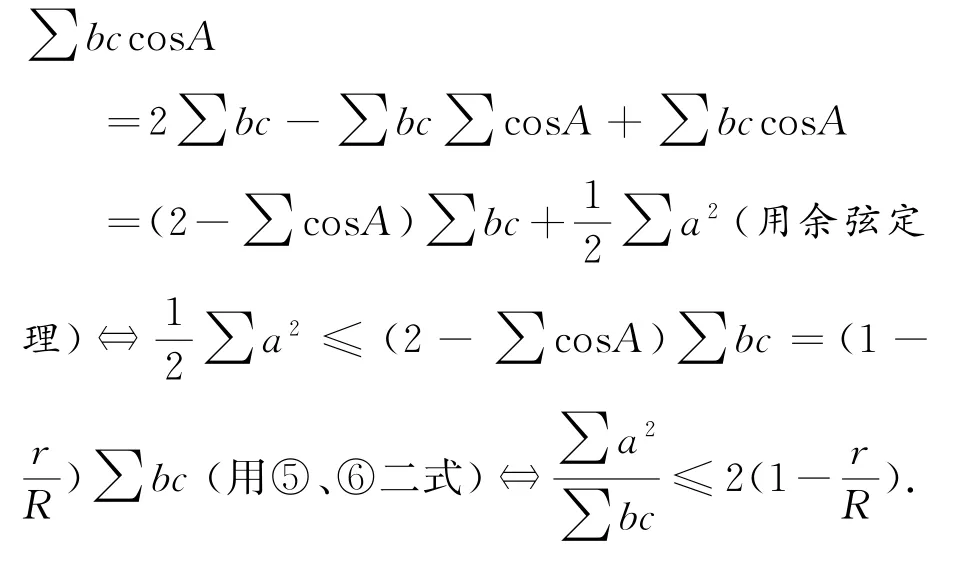
即定理与⑨式等价.

等价式5 在△ABC中,有

3 顺手牵羊“话”相关(不等式)

由不等式○11立获：

命题1 在△ABC中,有

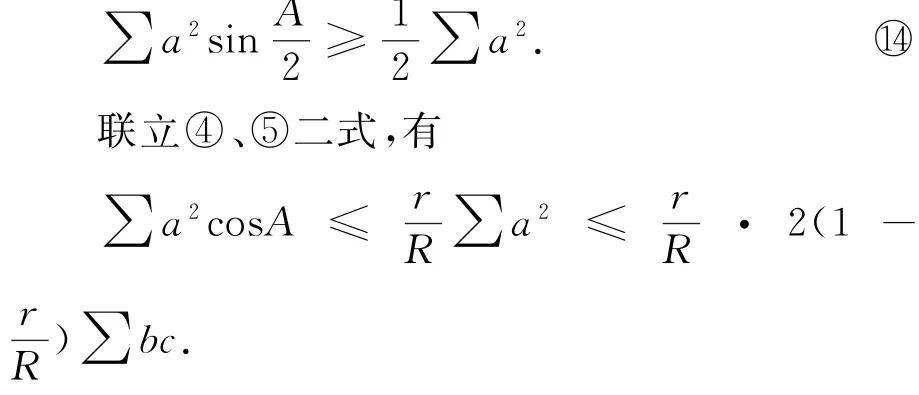
据此,得

命题2 在△ABC中,有

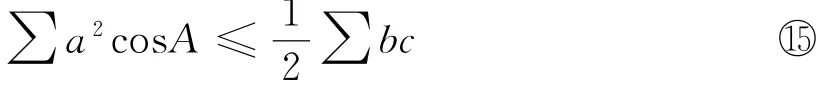
再联立⑦、⑨二式,又得：

命题3 在△ABC中,有

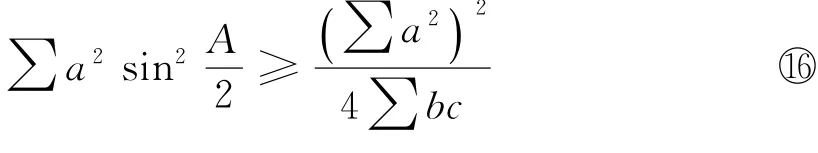
作为○13式的一个反向不等式当是：

命题4 在△ABC中,有

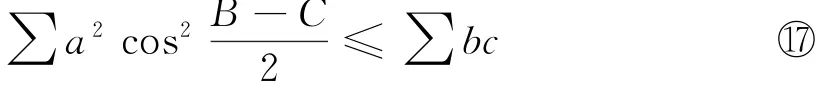
证明核心提示 应用⑩式去证明恒等式：

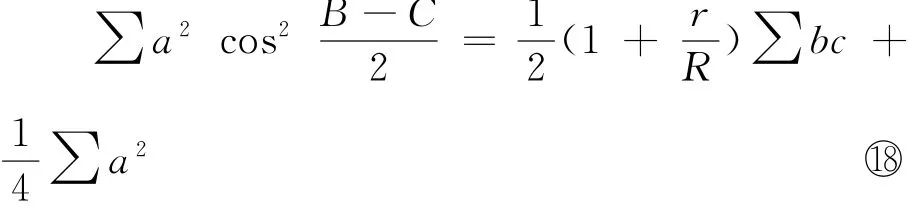
然后,⑨式应用于○18式,即可获证命题4(兴趣的读者请不妨一试).

另,⑨式用于○18式,还有

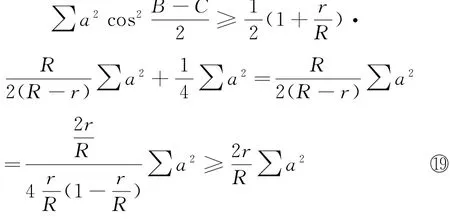
联立○19、④二式,便获：

命题5 在△ABC中,有

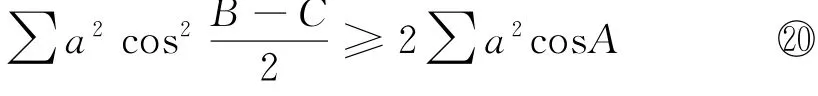
如若注意到③、④这两个反向不等式,我们又有以下的“节外生枝”：

命题6 在△ABC中,有

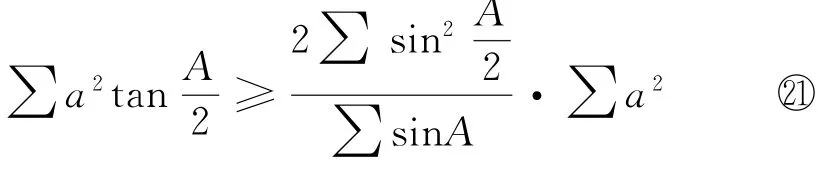
证明 注意到③、④两个反向不等式,③—④,并两边同时加∑a2,有

末了指出,证明三角形不等式的方法可以说是五彩缤纷、琳琅满目的,而利用母不等式的方法证明三角形不等式不乏是一门新型技术,它让人在“玩耍”中愉悦地接受数学.从某种意义讲,一个母不等式就是一个题库,是当下竞赛数学和初数研究命题的一门新学问和新艺术,是提高数学教师素质与专业素养的一条蹊径.

2017-10-10)