两类高考常考的双曲线
2017-12-18辽宁抚顺市四方高级中学孟庆杰邮编113122
辽宁抚顺市四方高级中学 孟庆杰 (邮编:113122)
两类高考常考的双曲线
辽宁抚顺市四方高级中学 孟庆杰 (邮编:113122)
离心率为和的两类双曲线,在高考试题中频频出现.他们就像一对兄弟,一会儿独立出现,一会儿联手出现.其实他们既有亲密关系,又有独立性质.如果能弄清他们的关系与性质,则此类高考试题顺利解决.
高考;双曲线;离心率
1 两类双曲线的关系及性质
1.1 基本性质(以焦点在x轴上为例)
设双曲线的实半轴为a,虚半轴为b,半焦距为c,离心率为e.
(1)基本关系

(2)本身关系
①离心率为 5的双曲线,焦点到渐近线的距离d=b=2a;离心率为的双曲线,焦点到渐近线的距离d=b=a.
1.2 相似性质
(1)与中点有关的性质
①已知双曲线的中心为坐标原点,F是双曲线的一个焦点.则双曲线的离心率为 5的充要条件是在双曲线上存在点P,使PF的中点恰为双曲线虚轴的一个端点.
充分性 由题意及中点坐标公式,得P(-c,2b),将点P坐标代入方程,得e= 5.
必要性 连接FB并延长到点P,使FB=BP,由中点坐标公式,得P(-c,2b).又e=5,所以将P坐标代入方程,得所以点P在双曲线上.焦点在y时,同理可证结论成立.
说明 当F为右焦点时,还有一个符合条件的P2;当F为左焦点时,也有两个符合条件的P3和P1,如图1.

图1
②已知双曲线的中心为坐标原点O,F是双曲线的一个焦点,点A为虚轴上一点且 OA 等于虚轴长,则双曲线的离心率为的充要条件是延长AF交双曲线于P点,且AF=FP.证明 由题意不妨设双曲线方程为=1(a>0,b>0),F(c,0),虚轴上的点A(0,2b),如图2.
充分性 由题意及中点坐标公式,得P(2c,-2b),将点P坐标代入方程,得e=.
必要性 连接AF并延长到点P,使AF=FP,由中点坐标公式,得P(2c,-2b).又e=,所以将P坐标代入方程,得-4=1,所以点P在双曲线上.焦点在y时,同理可证结论成立.
说明 当F为右焦点时,还有一个符合条件的P1;当F为左焦点时,也有两个符合条件的P3和P2,如图2.
(2)与等差数列有关的性质

图2

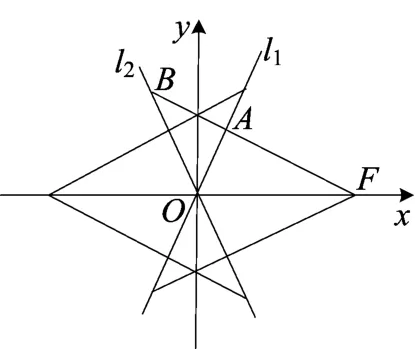
图3


说明 当F为右焦点时,还有一个符合条件的l;当F为左焦点时,也有两个符合条件的l,如图3.

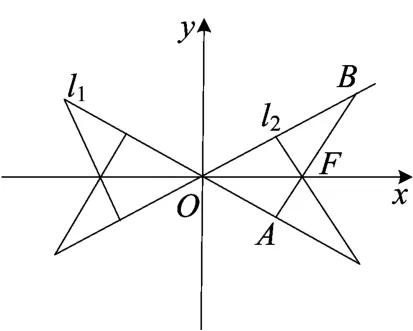
图4

说明 当F为右焦点时,还有一个符合条件的l;当F为左焦点时,也有两个符合条件的l,如图4.
①已知双曲线方程为 =1(a>0,b>0),抛物线方程为y=kx2+m.证明:
(i)若双曲线离心率为 5且km=1,则抛物线与双曲线的渐近线相切;(ii)若双曲线离心率为 5且抛物线与双曲线的渐近线相切,则km=1;(iii)若抛物线与双曲线的渐近线相切且km=1,则双曲线离心率为 5.
说明 双曲线方程为 =1(a>0,b>0),抛物线方程为x=ky2+m,仍然满足上述性质.
②已知双曲线方程为 =1(a>0,b>0),抛物线方程为x=ky2+m.证明:
(4)与三等分点和四等分点有关的性质
已知中心在坐标原点的双曲线的一个顶点为A,过A作直线l交双曲线的两条渐近线于B、C两点.
(i)由题意设直线l方程为y=-x+a,联立直线l与渐近线方程,求得所以b=2a,即e= 5.所以③成立.
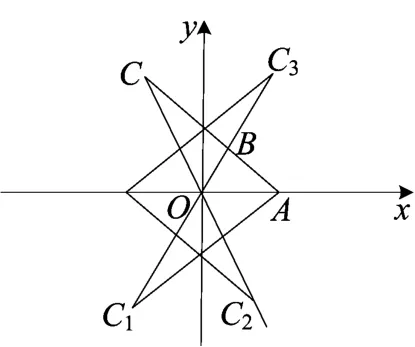
图5


说明 当A为左顶点时,直线l为AC2和AC3如图5,同理可证结论成立.曲线方程为1(a>0,b>0),A(a,0),如图6.
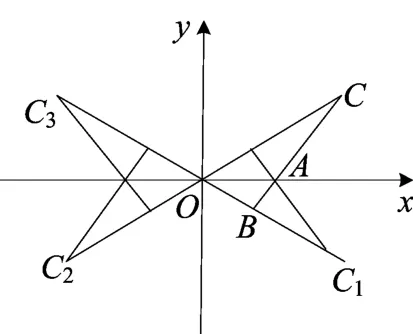
图6
(i)由题意设直线l方程为y=x-a,联立直线l与渐近线方程,求得即a=2b,所以3=(2b,2b),=(2b,2b),所 以3=.当直线l方程为y=-x+a变为直线AC1时如图6,同理可证结论成立,所以(i)成立.

说明 当A为左顶点时,直线l为AC2和AC3如图6,同理可证结论成立.当双曲线焦点在y轴上时,上述结论成立.

图7
证明 (i)(如图7)设直线l方程为y=3x+m,联立直线l与渐近线方程,求得又e=,即b=2a,由两点间距离公式得 P2A =m,P2B =m,所以 P2A =P2B .
当设直线l方程为y=-3x+m,即直线l为直线P1B1时,同理可证结论成立,所以(i)成立.
(ii)(如图7)设直线l方程为y=kx+m,联立直线l与渐近线方程,求得又e= 5,即b=2a,P2A =P2B,由两点距离公式化简解得k2=9,即直线l的斜率为3或-3,其中当直线l为直线P1B时,直线l的斜率为3;当直线l为直线P1B1时,直线l的斜率为-3,所以(ii)成立.
(iii)(如图7)设直线l方程为y=3x+m,联立直线l与渐近线方程,求得P2B,由两点间距离公式化简整理得b=2a,即e=5.所以(iii)成立.
说明:若过P2作直线l(如图7),同理可证上述结论成立.=1(a>0,b>0),x轴上有两点P1(-m,0)和P2(m,0)(m>0),过P1作不平行于y轴的直线l交双曲线渐近线于A,B两点(如图8),(i)若双曲线的离心率为,且直线l的斜率为或-,则PA =PB ;(ii)若双曲线的离心率为,22且PA =PB ,则直线l的斜率为或-22;(iii)若直线l的斜率为或-,且PA =PB ,则双曲线的离心率为.22
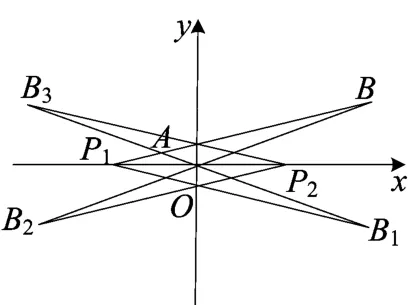
图8
(ii)(如图8)设直线l方程为x+ky+m=0,联立直线l与渐近线方程,求得,即a=2b,P2A =P2B,所以由两点间距离公式化简整理,得k2=9,即直线l的斜率为或-,其中当直线l为直线P1B时,直线l的斜率为;当直线l为直线PB时,直线l的斜率为-11,所以(ii)成立.
说明:若过P2作直线l(如图8),同理可证上述结论成立.
1.3 共同性质
证明(1) 当0<m<a时(如图9)
充分性 由题意直线l方程为bx+ay-ab=0,由梯形中位线性质,得2d=,解得a=2b或b=2a,所以双曲线的离心率为 5或

图9
必要性 由充分性证明得d1+d2=e=或e=,所以a=2b或b=2a,c=
当m=0时,点P1、P2与原点重合,d1=d2,同理可证成立;当m=a时,点P2与点A重合,d2=0,d1+d2=d1=,同理可证成立.
(2)当m>a时(如图10),由平面几何知识得d1-d2=2d.以下证明同(1)的证明.
说明 当a<m<b时,在y轴上存在两点P1(0,m)和P2(0,-m)(m≥0),则双曲线的离心率为或的充要条件是d+d=c,
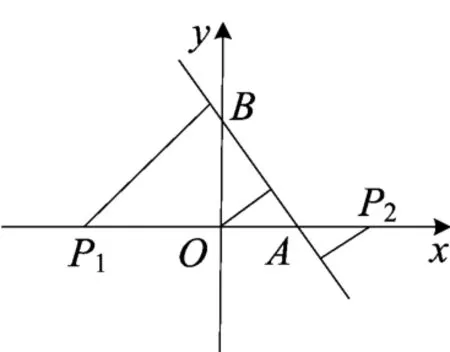
图10
12证明同上.当m>a且m>b时,结论同上面(2),证明同上.
2 两类双曲线在高考试题中的展示
2.1 基本问题争先恐后永不言败
(1)求双曲线方程
解 因为c=5,由基本性质,立即得b=1,a=2,所以所求方程为-y2=1,渐近线方程为y=±x.
说明 2009年重庆文,求离心率为 5的双曲线的方程;2011年广东,求离心率为的双曲线的方程;2014年天津,文理求离心率为的双曲线的方程;2015课标2文,求离心率为的双曲线的方程;2016年北京文,求离心率为的双曲线的方程;2016年天津文,求离心率为的双曲线的方程.
(2)找双曲线方程
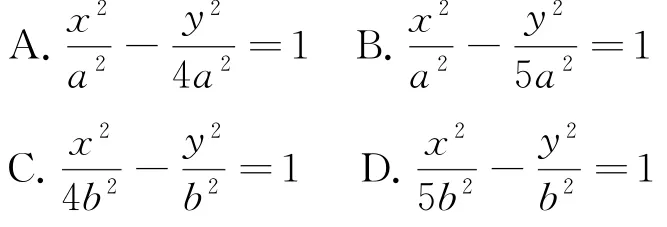
(3)求离心率
-y2=1的离心率等于 .
说明 2014年福建理,求离心率为 5.
(4)求渐近线
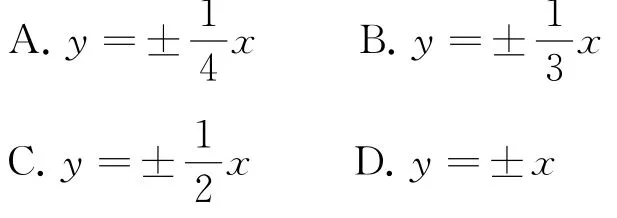
解 由基本性质C正确.
(5)求顶点到渐近线距离

解 由基本性质得C正确.
(6)综合

解 由题意a=2,a=2b,所以B正确.
解 由题意b=2a,又C1的右焦点为F(5,0),由基本性质得a=1,b=2.
例8 (2014年北京理)设双曲线C经过点(2,2),且与-x2=1具有相同渐近线,则C的方程为;渐近线方程为.
例9 (2015年上海文)已知双曲线C1、C2的顶点重合,C1的方程为-y2=1,若C2的一条渐近线的斜率是C1的条渐近线的斜率的2倍,则C2的方程为 .
解 由题意双曲线C2的a=2,a=b,所以所求方程为x2-y2=4.
2.2 独闯天下各显风彩
例10 (2008年全国1文)双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1、l2,经过右焦点F垂直于l1的直线分别交l1、l2于A,B两点.已知成等差数列,且同向.求双曲线的离心率.
2.3 兄弟联手打造奇迹

图11
解 设A(a,0),B(0,b)或A1(a,0),B1(0,b)(如图11),由共同性质1得s=2d=或s=2d1=c,当线段A1B1移动到线段AB时,满足s≥c,所以≤e≤.
2017-09-19)
