同分区配电网10 kV侧合环冲击电流分析

段若晨，姚 蓉，郑 可，庄军辉

(国网上海市电力公司市南供电公司，上海 200233)

同分区配电网10kV侧合环冲击电流分析

段若晨，姚 蓉，郑 可，庄军辉

(国网上海市电力公司市南供电公司，上海 200233)

随着电网供电可靠性要求的不断提高，在电网检修或故障时需要在配电网侧进行合环操作，进而可能产生较大的冲击电流，影响电网的安全稳定运行。利用数学建模的方法，针对同一分区不同容量主变的合环情况，给出了合环冲击电流计算公式，并以某条10 kV合环线路为例，结合实际监测数据和继电保护整定值，对正常情况及极端情况下线路冲击电流耐受情况进行分析，研究结果对电网实际运行具有较强的指导意义和参考价值。

配电网络；合环操作；冲击电流；建模分析

为了满足日益增长的电网供电可靠性要求，目前的配电网络均以合环结构搭建[1-2]，当某条线路需要进行检修或发生故障时，即可通过合环操作，不停电地将负荷进行转移。然而，当合环点两端主变处于不同分区或者同一分区但容量不同时，由于所带负荷不同，两段母线电压及相角均会有所偏差，使得合环瞬间会造成较大的冲击电流及稳态合环电流，会直接影响到电网的安全稳定运行[3]。

由于电网不同分区合环情况往往较为严重，因此受到关注较多，对于同分区10 kV侧合环情况关注较少[4-5]。同时，由于目前变电站升级改造较多，同分区不同容量合环情况也逐渐增多，引起的合环冲击电流需要引起足够重视。

本文主要利用数学建模方法，针对同一分区不同容量两主变合环情况进行分析，给出合环冲击电流计算公式，同时结合实际监测数据和继电保护整定情况，分析计算负荷最高时和正常工况下该线路的合环情况，以验证该方法的可行性。

1 建模分析

以A站2号主变(容量80 MVA，变比110/10)和B站2号主变(容量20 MVA，变比35/10)的10 kV侧合环为例进行分析。其上级变电站分别为同一分区的C、D 220 kV变电站，并通过联络线直接连接，因此认为环路220 kV侧电压和相角保持一致。而A、B两站10 kV侧则通过两条出线电缆a、b，在配电站内的10 kV分段负荷闸刀进行联络，进而构成合环回路，其合环示意图如图1所示。

图1 同分区配电网10 kV侧合环示意图

由图1可见，由于两站主变容量不同，所带负荷有较大差距，因此两站10 kV母线的电压及相角均不相同，合环的瞬间会在连接两站的线路上产生较大的冲击电流。此后，环流会通过环网，形成较大的稳态电流。由于合环回路均为纯电缆线路，其阻抗较架空线路更小，合环电流相对而言会更大。图1中各主变、线路参数分别如表1、表2所示。

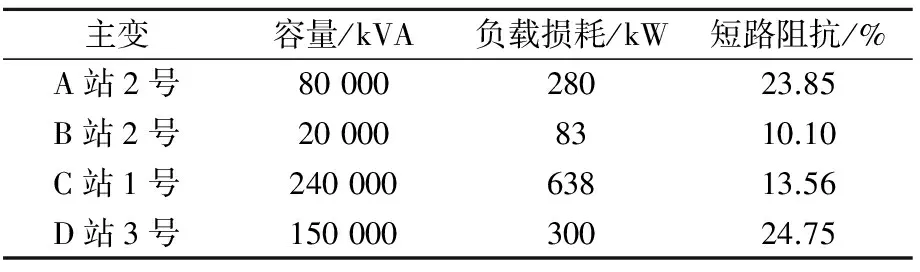
表1 各主变参数

表2 各线路参数

2 计算过程

首先建立合环电流暂态过程的单相等值电路方程，即：

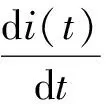
(1)

式中e(t)——等效电路的电动势；Em、α——分别为合环时刻两10 kV母线的电压差和相角差；R、L——分别为等效电路的总电阻和总电抗。

由于该方程属于时域非线性微分方程，可通过拉普拉斯变换，将其转化为复频域中的代数方程进行求解。

对式(1)两端取拉普拉斯变换，得：

E(s)=RI(s)+sLI(s)-Li(0_)

(2)

由于合环前，电路中没有电流通过，因此电感中的初始电流为零，因此有：

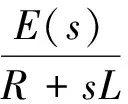
(3)

令：

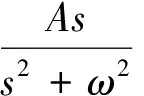
(4)

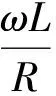
(5)

对式(4)进行拉普拉斯反变换并带入式(5)，得到时域中合环电流的完全表达式为

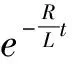
(6)

由于三相对称，只需将和代入式(6)，即可得到其余两相的全电流表达式。

由式(6)可以看出，合环电流由交流分量iac和直流分量idc两部分组成：

(7)

式中iac——合环稳态周期分量，其幅值大小取决于合环点两侧电压差和环网总阻抗；idc——呈指数规律衰减的非周期分量。

idc的初始值idc0取决于合环时刻的初始状态，衰减时间常数由环路中电阻与电感的比值决定。直流分量值越大，合环电流瞬时值就越大。在合环点两侧电压差和环路阻抗一定的情况下，其大小由合环点两侧电压相角差所决定，当α满足α-φ=90°时，idc0的绝对值达到最大iM，将在合环操作约1/2个周期(0.01 s)后出现，即：

iM=(1+e-0.01R/L)Im

(8)

由此可见，合环电流由合环点两侧母线电压差、所带负荷及环网阻抗共同决定，为保证合环安全，应采取措施，尽量减小合环点两侧的电压差及相角差。

3 分析结果

利用SCADA系统监测数据进行分析计算。由于母线电压及所带负荷是随时变化的，以2016年7月28日和2016年10月28日12点的母线数据为例进行分析，能够分别代表最高负荷和平日负荷状态。同时，为了能够准确判断环流对电网的影响，需要参考a和b两条合环联络线的继电保护整定情况，这两条线路均采用反时限过流保护，整定值如表3所示。

表3 a、b线路继电保护整定值

首先对2016年10月28日数据进行分析，电压、功率及电流情况如表4和表5所示。分别计算电压差及角差，并根据式(6)计算三相的冲击电流及稳态电流，如表6所示。计算结果显示，三相冲击电流达到了两条线路平日负荷电流的十几倍甚至几十倍以上，同时已超过b线反时限过流保护的启动电流整定值，然而由于冲击电流衰减时间较短，很快便会达到稳态电流，因此不会引起线路保护动作。

表4 2016年10月28日电压、功率监测数据

表5 2016年10月28日电流监测数据

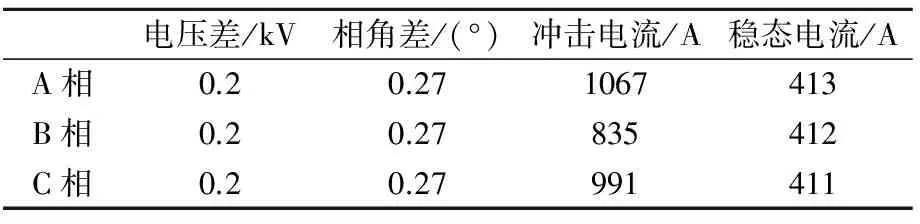
表6 2016年10月28日三相合环电流计算结果

随后选取2016年7月28日全年最大负荷日数据进行分析，该日两站所带负荷量为2016年10月28日的三倍多，因此作为极端情况进行分析。负荷情况如表7、8所示，计算结果如表9所示。计算结果显示，合环电流相较平时情况下有大幅度增加，其中A、C相冲击电流已超过b线反时限过流保护启动电流三倍，并且稳态电流也已超过两条线路保护的启动电流，若合环后未能尽快解环完成后续操作，很有可能引起线路保护动作。同时稳态电流过大，也有可能对上级电网设备及线路造成损害，对电网正常运行造成影响。

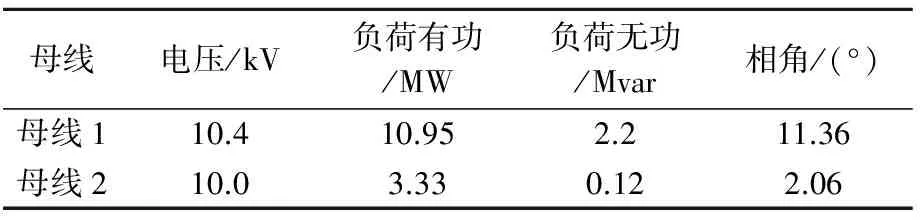
表7 7月28日电压、功率监测数据

表8 7月28日电流监测数据

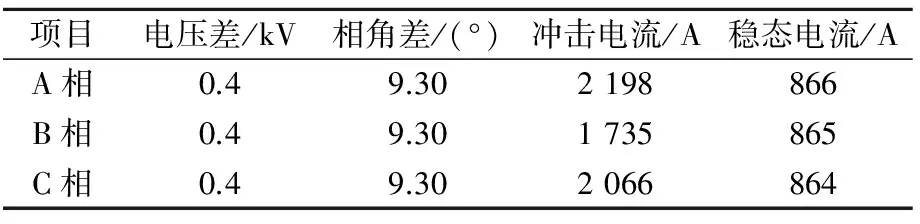
表9 7月28日三相合环电流计算结果

4 结语

本文主要针对同分区不同容量主变10 kV侧合环情况进行分析计算，由于目前变电站均配备了AVC装置，可在电压发生偏移时进行自动调节，因此10 kV侧电压偏差一般不会超过5%。然而，当两站主变容量不同时，所带负荷偏差较大时，两母线存在一定的角差，同样会对合环电流造成显著影响。根据典型数据的分析结果显示，配网合环存在继电保护装置误动风险，因此建议不同容量主变合环一定要在负荷低谷时进行，同时在合环前，尽量通过有载调压装置和无功补偿装置，调整合闸两侧母线电压幅值和相角保持一致，以控制合环电流大小，保证电网的安全可靠运行。

[1] 王友怀,杨增力,周虎兵,等.相序不对应合环对继电保护的影响[J].电力系统自动化,2013,37(18):99-102.

WANG Youhuai, YANG Zengli, ZHOU Hubing, et al. Impact of power transmission lines ring closing with a wrong phase sequence on protective relays[J].Automation of Electric Power Systems, 2013, 37(18): 99-102.

[2]王友怀,杨增力,周虎兵,等.相序不对应合环对继电保护的影响[J].电力系统自动化,2013,37(18):99-102.

WANG Youhuai, YANG Zengli, ZHOU Hubing, et al. Impact of power transmission lines ring closing with a wrong phase sequence on protective relays[J].Automation of Electric Power Systems, 2013, 37(18): 99-102.

[3]陈霄，王磊，李扬．配电网合环冲击电流的分析[J]．电力自动化设备，2005，25(4)：40-42．

[4] 汲亚飞,赵江河.辐射型配电网合环稳态电流计算方法研究[J].电力系统保护与控制,2009,37(12):15-19.

JI Yafei, ZHAO Jianghe. Calculation of the loop closing steady-state current in radial power distribution network[J].Power System Protection and Control, 2009, 37(12): 15-19.

[5]邹俊雄,周冠波,付轲,等.10 kV配网合环转电计算模型与试验分析[J].电力系统保护与控制,2010,38(8):144-148.

ZOU Junxiong, ZHOU Guanbo, FU Ke, et al. Electromagnetic loop closing calculation model and experimental analysis on 10 kv distribution network[J].Power System Protection and Control, 2010, 38(8): 144-148.

Analysisof10kVSideLoop-ClosingSurgeCurrentinDistributionNetworksoftheSamePartition

DUAN Ruochen, YAO Rong, ZHENG Ke, ZHUANG Junhui

(State Grid Shanghai Shinan Power Supply Company, Shanghai 200233, China)

With the improvement of power supply reliability requirement, a large surge current may be generated by closing loop in distribution network in the case of power grid maintenance or fault, which will infect the safe and stable operation of grid. This paper presents the formula to calculate the surge current during closing loop of different capacity transformers in the same partition by mathematical model. A typical 10 kV loop line has also been studied to analyze the tolerance situation of surge current under normal and extreme situation based on the setting value of relay protection. The research results have significant value of guidance and reference for the grid operation.

distribution network; loop closing; surge current; model analysis

10.11973/dlyny201705004

段若晨(1988—)，男，博士，工程师，从事电力调度工作。

TM744

A

2095-1256(2017)05-0507-03

2017-08-06

(本文编辑：赵艳粉)