解决三角恒等变形问题六种法则

江西 陈国林

解决三角恒等变形问题六种法则

江西 陈国林

三角恒等变换是高考考试中每年必考的内容，不仅在考题中有小题出现，也会结合大题进行考查，大部分题目以中档题为主，本文主要提出了六种方法去处理三角恒等变形问题供大家参考.

一、利用角变换妙解三角恒等变形问题

( )

故选D.

【评注】三角变换是指角(“配”与“凑”)、函数名(切割化弦)、次数(降与升)、系数(常值“1”)和运算结构(和与积)的变换，其核心是“角的变换”.

角的变换主要有：已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换.

二、妙用配凑角解三角恒等变形问题

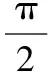
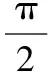
三、根据函数名的差异妙转化解三角恒等变形问题

【解析】解法1:原式=sin50°(1+tan60°tan10°)

=1.

【评注】名的变化：利用同角三角函数的基本关系，将不同名的三角函数化成同名的三角函数，以便于解题.经常用的手段是“切化弦”和“弦化切”.基本思路有：(1)化非特殊角为特殊角；(2)化为正负相消的项，消去后求值；(3)化分子、分母使之出现公约数，进行约分求值.

所以sinCcosA+sinCcosB=cosCsinA+cosCsinB,

即sinCcosA-cosCsinA=cosCsinB-sinCcosB,

得sin(C-A)=sin(B-C)，

所以C-A=B-C,或C-A=π-(B-C)(不成立).

四、利用常值变换妙求三角恒等变形问题

五、活用整体换元法妙求三角恒等变形问题

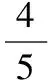
六、构造对偶式法妙解三角恒等变形问题

【例6】求cos20°cos40°cos80°sin20°sin40°sin80°的值.

【解析】设x=cos20°cos40°cos80°，y=sin20°sin40°sin80°，

xy=cos20°cos40°cos80°sin20°sin40°sin80°

【评注】在求值，化简的三角问题时，灵活运用构造对偶式的对偶的数学思想，合理地构造形如xy的对偶函数，进行和、差、积等运算，则问题可得到解决.

【变式6】求sin210°+cos240°+sin10°cos40°的值.

【解析】设x=sin210°+cos240°+sin10°cos40°，

y=cos210°+sin240°+cos10°sin40°,

x+y=sin210°+cos240°+sin10°cos40°+cos210°+sin240°+cos10°sin40°

=1+1+sin10°cos40°+cos10°sin40°

=2+cos40°,

因为-cos20°+cos40°+cos80°

=-cos20°+cos(60°-20°)+cos(60°+20°)

=-cos20°+cos60°cos20°+sin60°sin20°+cos60°cos20°-sin60°sin20°

=2cos60°cos20°-cos20°

=cos20°-cos20°

=0.

江西省赣南师范大学科技学院)