打破常规 巧妙秒杀——两种策略妙解圆锥曲线

四川 杨铁坪

打破常规 巧妙秒杀
——两种策略妙解圆锥曲线

四川 杨铁坪

圆锥曲线在高考中是重要考点，同时也是难点.而选择填空题中圆锥曲线的考查历年来备受命题人员的青睐.在圆锥曲线解题中若能巧妙应用“特殊”解“一般”的数学思想、定义与几何相结合的思想，将事半功倍.下面分别通过几道高考实例，来探究求解圆锥曲线小题的两种策略.

一、“特殊”到“一般”，化繁为简

在圆锥曲线中，求解离心率的题目通常落脚在a,b,c三者的关系，在解题过程中，参数太多对考场上紧张的考生来说是不利的，那么是否可以通过一些手段来减少参数，化繁为简解决问题呢？接下来以2012年高考新课标的一道题为例进行探究.

( )

因为∠PF1F2=30°，

所以∠PF2D=60°,∠DPF2=30°，

由△F2PF1是底角为30°的等腰三角形⟹∠PF2D=60°，|PF2|=2c且PD⊥x轴，则DF2=c，

【评注】方法一：属于常规解法，可以看出参数特别多，稍显繁杂；方法二：取“a=1”，明显简便许多，这里我们运用了特殊到一般的思想，至于在应用过程中“特殊化”参数与“特殊化”值的选取，需要根据题目灵活变化.下面再通过两道题目来验证此方法的有效性.

因为AM=AN=b且∠MAN=60°，不妨设b=1，

联立解得a2=3⟹c2=a2+b2=4，

二、定义与几何，妙解题目

定义与几何的考查在试卷中层出不穷，因此在学习过程中，善于利用定义与几何的关系，通过定义与几何关系的转化大大地简化运算，对于解决圆锥曲线问题有着不可小觑的作用.

( )

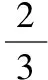
【评注】方法一：常规办法，设直线解点，找几何关系构造方程，思路简单，计算相对复杂；方法二：结合椭圆定义及性质，运用几何关系，快速看出tan∠EAB与tan∠MBA的关系.定义与几何的结合快速解出答案，大大节约了时间.此处列举几种常考几何关系：①对称关系(椭圆，双曲线等圆锥曲线均具有对称性)；②圆直径所对的圆周角是直角；③抛物线的定义:抛物线上的点M到准线距离为d，F为抛物线焦点，则d=|MF|.下面我们运用“方法二”来做几道练习题.

( )

A.3 B.4

C.5 D.6

【解析】如图所示，易知EF∥OM,EF∥ON,

且|OA|=|OB|,|AF|=a+c,|BF|=c-a，

( )

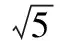
【解析】如图所示，过焦点F作MN的垂线,垂足为C，FM的倾斜角∠MFx=60°且MN⊥y轴⟹∠FMN=60°，

由抛物线定义知|MN|=|MF|且|NC|=2|OF|=2，

所以△MNF为等边三角形,则C为MN中点，

所以|MN|=2|NC|=4，

【变式训练3】(2017·全国卷Ⅱ理)已知F是抛物线C:y2=8x的焦点，M是C上一点，FM的延长线交y轴于点N．若M为FN的中点，则|FN|=________．

四川省西华师范大学数信学院)