应用焦半径公式的角度式解题

浙江 杨育池

应用焦半径公式的角度式解题

浙江 杨育池

众所周知，圆锥曲线上的任意一点M与圆锥曲线焦点F的连线段MF的长度，叫做圆锥曲线焦半径．焦半径是圆锥曲线中的重要几何量之一，因其能与圆锥曲线的离心率、过焦点的直线斜率(或倾斜角)、向量(定比分点)和焦点弦长等知识交汇，故倍受命题人青睐，在近几年的高考题中频频亮相，作为客观题中的压轴题、甚至大题进行考查，以测试考生数学知识与思想方法的掌握和解题策略的运用．

我们考虑到焦半径由其所在直线的倾斜角唯一确定，运用这一关系研究处理与焦半径有关的问题，计算可能更显快捷．下面我们首先推导椭圆的焦半径公式的角度式.

一、认识焦半径的角度式

由余弦定理，有|MF1|2+|F1F2|2-2|MF1|·|F1F2|cosα=|MF2|2，

又由椭圆的定义，有|MF2|=2a-|MF1|，

故|MF1|2+4c2-4c|MF1|cosα=(2a-|MF1|)2，

下面再从近三年高考题与大学自主招生题及竞赛题中撷取几例说明公式的应用.

二、公式的简单应用

1 计算焦半径或焦点弦长

( )

C.3 D.2

故由a2=b2+c2，解得c=2，所以a=3,b2=5，

2 计算与焦半径有关直线的斜率

【例3】(2016·四川卷理8)设O为坐标原点，P是以F为焦点的抛物线y2=2px(pgt;0)上任意一点，M是线段PF上的点，且|PM|=2|MF|，则直线OM斜率的最大值为

( )

3 计算与焦半径有关平面图形的面积

【例4】(2016·全国卷Ⅰ理20)设圆x2+y2+2x-15=0的圆心为A，直线l过点B(1,0)且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E.

(Ⅰ)证明|EA|+|EB|为定值，并写出点E的轨迹方程；

(Ⅱ)设点E的轨迹为曲线C1，直线l交C1于M,N两点，过B且与l垂直的直线与圆A交于P,Q两点，求四边形MPNQ面积的取值范围.

【解析】(Ⅰ)圆的半径r=4，故|AC|=|AD|=r，

又BE∥AC，则|BE|=|ED|.

故|EA|+|EB|=|EA|+|ED|=|AC|=4为定值.

因此，由椭圆的定义，

(Ⅱ)如图，由(Ⅰ)知，直线l过椭圆的右焦点B(1,0)，记l的倾斜角为α，则0lt;αlt;π，

又点A到PQ的距离d=|AB|·|cosα|=2|cosα|，

故四边形MPNQ面积

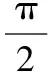
4 计算圆锥曲线的特征量

(Ⅱ)若直线MN在y轴上的截距为2，且|MN|=5|F1N|，求a，b.

因为|MN|=5|F1N|，即|F1M|=4|F1N|，

消去c得3(a-2)=5(a-4)，即a=7.

(Ⅱ)记PF1的倾斜角为α,椭圆的半焦距为c，

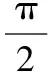
因为PQ⊥PF1，故|PF1|=|F1F2|·cosα=2ccosα，

|PF2|=|F1F2|sinα=2csinα，

由椭圆的定义，有2c(cosα+sinα)=2a，

【提示】记PF1的倾斜角为α,椭圆的半焦距为c.

因为PQ⊥PF1，故|PF1|=|F1F2|·cosα=2ccosα，

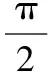
由|PF1|=|PQ|，

整理上式，有

【提示】记AF1的倾斜角为α，

由|AF1|=3|BF1|得，3(a-ccosα)=a+ccosα，

在△ABF2中，由余弦定理，

有|AF2|2+|BF2|2-2|AF2|·|BF2|·cos∠AF2B=|AB|2，

整理得4e4-12e2+5=0，即(2e2-1)(2e2-5)=0，

5 计算定值

(Ⅰ)求椭圆L的方程；

(Ⅱ)求λ1+λ2的值；

(Ⅲ)求△F1AC的面积S的最大值.

(Ⅱ)如图,设直线F2A,F1A的倾斜角分别为α,β，

由椭圆定义，有

(Ⅲ) 因为S=S△F1F2A+S△F1F2C

当且仅当sinα=1即AC⊥x轴时等号成立.

浙江省象山中学)