对一道高考题的探究

湖北 聂文喜

对一道高考题的探究

湖北 聂文喜

( )

本题以三角函数为载体，以对称轴、对称中心、最小正周期为切入点，主要考查学生数学基本知识、数学方法、数学思想的掌握情况，考查分析问题和解决问题的综合能力，入口较宽，解法多样，同时又能区分不同思维层次的学生,本文尝试从不同视角寻求突破．

1.解法探究

【点评】逐一验证法是解答选择题的一种方法，主要是从结论反代，看是否适合条件.由于数学选择题答案的唯一性，只要判断一个选择支正确即可.

又f(x)最小正周期大于2π，

2．题源探究

( )

A．11 B．9

C．7 D．5

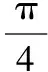
故函数f(x)的最小正周期为T=π．

【点评】已知函数f(x)=Asin(ωx+φ)(A,ω,φ为常数，Agt;0，ωgt;0)，则

3．变式探究

( )

( )

( )

( )

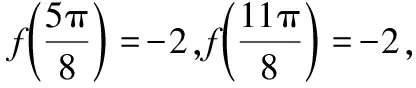
【点评】已知函数f(x)=Asin(ωx+φ)(A,ω,φ为常数，Agt;0，ωgt;0)，则

(1)若x=x1和x=x2均为函数f(x)图象的对称轴，且f(x1)=f(x2)，则|x2-x1|=kT(k∈Z，T为f(x)的最小正周期)；

4．拓展探究

上述高考题及变式题中x=x1和x=x2均为函数f(x)的对称轴或零点，若x=x1和x=x2中有一个不是函数对称轴或零点，情况如何呢？

( )

( )

( )

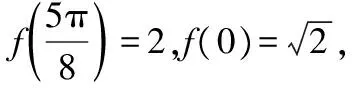
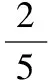
湖北省广水市第一高级中学)