基于GPR-PSO模型的永磁同步电机气隙磁密波形优化

，

(广东工业大学，广东广州 510006)

基于GPR-PSO模型的永磁同步电机气隙磁密波形优化

杜晓彬，邓建华

(广东工业大学，广东广州 510006)

为了使永磁同步电动机气隙磁密波形具有良好的正弦性，以气隙径向磁密波形的谐波畸变率为目标，磁钢的偏心距、极弧系数、磁钢厚度以及磁钢的充磁方向为因素变量进行优化。引进了正交实验设计的方法合理地安排了实验因素变量的搭配，利用有限元软件ANSYS Maxwell 2D仿真分析得到数据样本集，采用了高斯混合回归模型(GPR)对数据样本集进行拟合，得到拟合回归模型。采用方差分析方法分析了各个因素对于谐波畸变率的影响的程度。将拟合回归函数作为适应度函数，通过粒子群算法(PSO)寻优，得到最优的磁钢参数。以一台48槽8极的永磁同步电动机为例进行仿真实验，结果表明,通过GPR-PSO模型的方法可以有效降低永磁同步电机的气隙磁密波形畸变率，使波形得到良好的改善。

谐波畸变率；正交设计；高斯混合回归模型；粒子群算法

0 引言

永磁同步电动机(PMSM)由于具有良好的运行特性、体积小、功率密度高等优点，且结构简单，没有电刷和换向器产生火花、磨损，被大量应用于生产实践中[1～3]。其中，转矩波动是PMSM突出的主要问题之一，转矩波动很大程度上由非理想的正弦反电动势波形造成的。电机气隙磁密波形的正弦性影响了反电动势波形的正弦性，故优化PMSM气隙磁密波形，降低气隙磁密波形的谐波畸变率有十分重要的意义[4～5]。

文献[6]分析了PMSM不同偏心距下的气隙磁场波形及其对应的谐波含量，获得了气隙磁场波形畸变率与偏心距之间的关系曲线，得出了最优偏心距。文献[7]利用ANSYS有限元分析软件计算分析了不同极弧系数和偏心距对磁场正弦畸变率的影响。文献[8]为使PMSM空载气隙磁密波形具有良好的正弦性，分析了电机气隙长度及磁极厚度对谐波畸变率的影响。文献[9]分析了磁钢的充磁方向对于气隙磁密波形谐波畸变率的影响。

本文以一台48槽8极表贴式磁钢PMSM为例，针对影响永磁同步电机气隙径向磁密谐波畸变率的四个因素，即磁钢偏心距、极弧系数、磁钢厚度、以及磁钢的充磁方式，通过正交设计的方法安排了实验搭配，构建了数据样本集，利用方差分析方法分析了各个因素变量对于谐波畸变率的影响的大小。通过GPR模型对数据样本集进行拟合，构建适应度函数。利用PSO算法进行寻优，得到最优的磁钢参数，达到对PMSM气隙磁密波形进行优化的目的。

1 PMSM模型建立及气隙磁密波形谐波分析

1.1 PMSM 模型建立

本文以一台48槽8极的PMSM为例，通过ANSYS Maxwell 2D仿真软件对PMSM额定负载情况下进行仿真计算，电机相关参数见表1，电机模型如图1所示。

表1 PMSM相关参数

图1 PMSM有限元模型

电机径向气隙磁密的波形图分析结果如图2所示。可以看出，径向气隙磁密幅值达到1.08T，基本符合电机设计的要求。

图2 PMSM径向气隙磁密波形

1.2 PMSM气隙磁密波形谐波分析

利用有限元软件的快速傅里叶分析FFT功能对PMSM径向气隙磁密波形进行傅里叶分析，并利用Matlab软件绘制各次谐波分量图如图3所示。由于高次谐波分量幅值较低，本文只绘制出前15次数谐波分量幅值。可以看出，基波幅值为0.934T，谐波次数主要为奇数次谐波。计算气隙磁密波形的谐波畸变率，可得到THD值为17.62%。

图3气隙磁密波形各次谐波分量

2 建立样本数据集及方差分析

2.1 正交设计与样本数据集建立

本文采用的影响因素有四个，即偏心距、极弧系数、磁钢厚度、充磁方式。考虑到实际工艺情况，各个变量的取值范围为：偏心距18～21mm，极弧系数0.6～0.9，磁钢厚度4.2～4.5mm，充磁方向为平行充磁和径向充磁。由于充磁方向变量为虚拟变量，自由度为1，设置平行充磁为基础类型，充磁方式变量按照式(1)处理，前三个变量为连续变量，则设置因素变量水平表如表2所示。

(1)

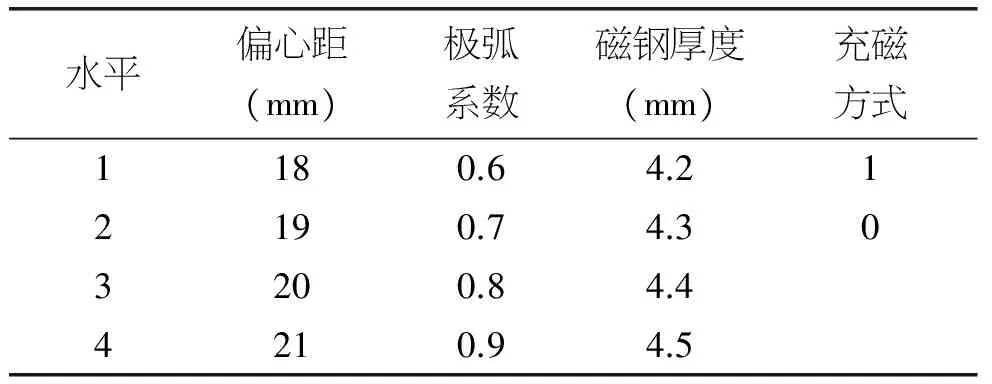
表2 因素变量水平表

设计的实验因素较多，使用普通的多因素设计方法需要的样本例数比较多，实验的时间比较长。而采用正交设计，可以将各实验因素的不同水平之间均衡搭配，用有适量的、代表性的处理组合数，提供充分的信息。由于没有直接的可用的混合正交表，利用SPSS软件给出正交表如表3所示，并仿真分析计算得到不同搭配组合下的THD值。

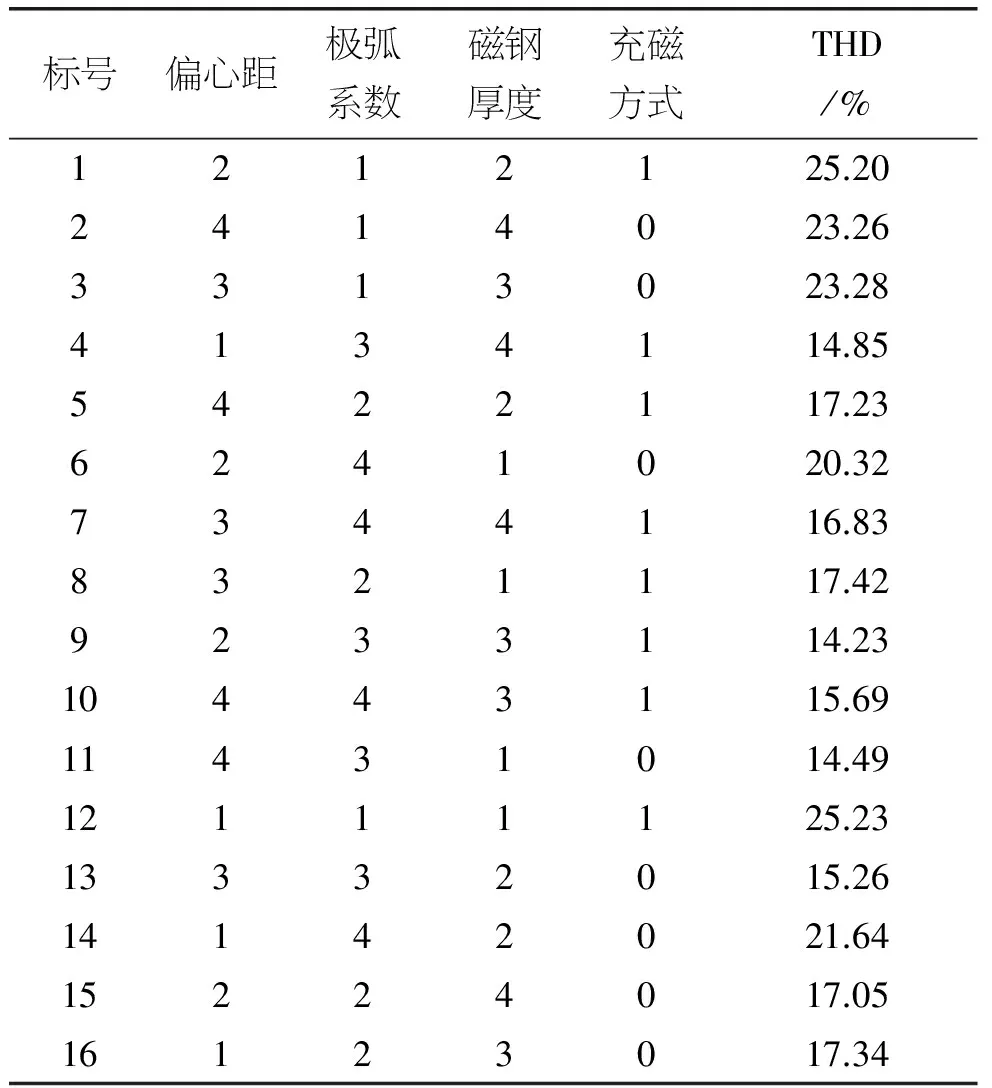
表3 正交设计实验结果

采用表3中数据建立样本数据集合Ω=(Xi,Yi)。其中Xi=(X1,X2,X3,X4)，X1至X4分别表示偏心距、极弧系数、磁钢厚度、充磁方式 ，Yi表示THD值。

将谐波畸变率THD随着因素的水平变化的情况用图4表示。由图可知，最优的组合是Xbest=(X14,X23,X33,X41)=(21,0.8,4.4,1)。

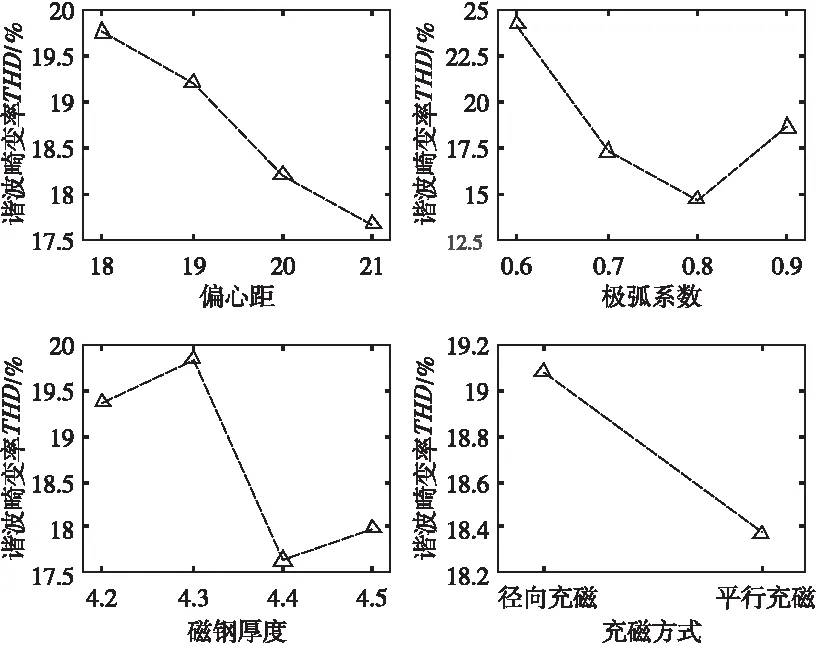
图4 THD值随因素水平变化情况

2.2 实验数据方差分析

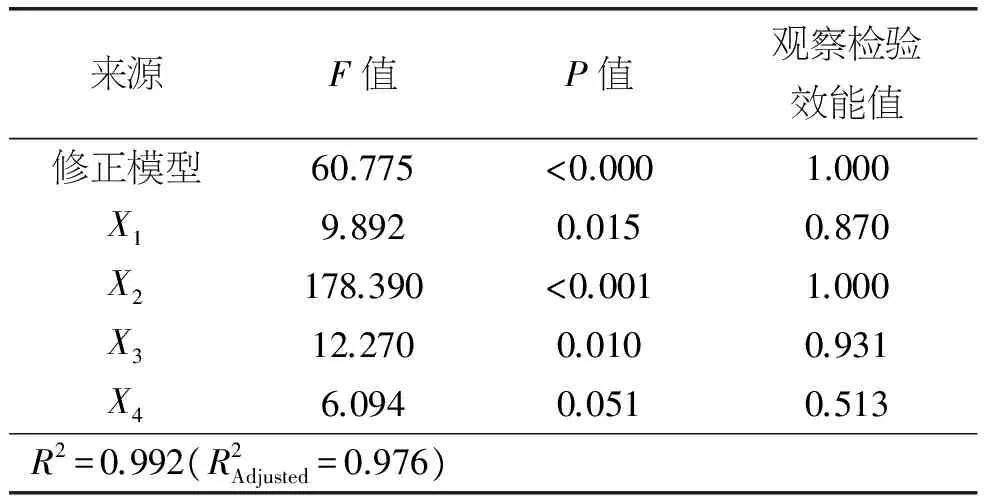
表4 方差分析结果

3 数学模型回归及粒子群算法寻优

在PMSM中，本文考虑的电机参数与THD值之间呈现非线性关系，且正交设计分析只能给出最优解大致的结果。为了得到精确结果，下文将通过GPR模型进行拟合回归，构建PSO模型的适应度函数，并通过PSO进行寻优。

3.1 高斯混合回归模型(GPR)回归分析

对于实验数据集合Ω=(Xi,Yi)和预测数据集合Ω*=(Xi*,Yi*),则Ω=(Xi,Yi)与Ω*=(Xi*,Yi*)的均值与协方差可以表示为

(2)

对于Ω=(Xi,Yi)，概率分布密度函数可以通过多个单高斯模型的加权函数来表示，即

(3)

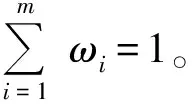
其次，通过EM算法迭代计算参数的估计值，直到迭代条件结束。具体方法如下：(E步骤)由K-means聚类结果计算ωi后验概率，即估计的每个单高斯模型的权值；(M步骤)基于计算的后验概率，更新估计高斯模型的参数μiy、∑iy。重复以上E、M步骤，直到三个参数估计值趋近于稳定。

通过估计得出的参数值，建立GPR模型，并通过此模型进行预测，若已知X*，则Y*的预测回归值可以表示为

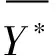
(4)

fi(y)=μiY*+∑iY*Y∑iY-1(Y-μiY)。

本文采用将样本数据集分成三类的方式进行拟合，则GPR回归模型预测实验值的结果如图5所示，其中横坐标为实验的标号，纵坐标为THD值。由图5可知，GPR模型的回归值误差较小。其中，GPR模型的平均误差率为0.02%，可以看出，GPR回归拟合模型精度较高，可用于PSO模型的适应度函数。

图5 GPR模型回归结果

3.2 粒子群算法(PSO)寻优

PSO算法是基于群体的演化算法，是根据自然界鸟类寻找食物的行为所演变的人工智能算法。每一个粒子都对应着一个解，且都有对应的速度和位置，并被适应度函数所评价[13、14]。粒子根据社会认知与个体认知两个方面不断更新自身的速度和位置，直到寻找到最优解。粒子i在第k次的迭代公式如下

Vidk+1=ωVidk+c1r1(Pbestidk-Xidk)+

c2r2(Gbestdk-Xidk)

(5)

Xidk+1=Xidk+Vidk+1

(6)

式中，ω—惯性权重；c1，c2—加速度因子；r1，r2—[0,1]之间随机数；Pbest—个体极值点的位置；Gbest—全局极值点的位置。

以X=(X1,X2,X3,X4)为粒子位置，将GPR模型拟合函数作为适应度函数，设置进化代数为50代，种群规模为80，C1=C2=1.5，进行寻优，结果如图6所示。最优的适应度值稳定在13.0566，即谐波畸变率为13.06%，此时粒子的位置为Xpso=(21,0.7976,4.3993,0.9995)。考虑实际工艺情况，取值情况为偏心距21mm，极弧系数0.8，磁钢厚度4.4mm，采用平行充磁法方式。

图6粒子群算法寻优结果

3.3 ANSYS-Maxwell 2D有限元仿真分析验证

在PMSM电机模型中，将偏心距、极弧系数、磁钢厚度、充磁方式按照PSO求解的结果进行设置，仿真结果波形图如图7所示。由图可知，气隙磁密幅值达到1.06T，满足电机设计的要求。对波形进行谐波分析，分析结果如图8所示，此时谐波畸变率为13.23%，与粒子群算法寻优的结果基本一致，可以看出，谐波畸变率比原来降低了4.39%，波形得到改善。

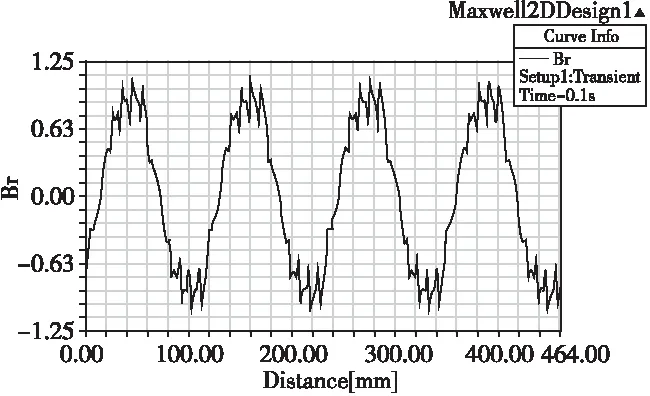
图7优化后PMSM径向气隙磁密波形

图8优化后气隙磁密波形各次谐波分量

4 结语

提出了一种优化永磁同步电动机气隙磁密波形的方法：以气隙径向磁密谐波畸变率为目标，偏心距、极弧系数、磁钢厚度、充磁方式为变量，通过正交设计与有限元仿真分析形成数据样本集；通过方差分析得出因素变量对谐波畸变率的影响大小的顺序：极弧系数gt;磁钢厚度gt;偏心距gt;充磁方式；通过GPR模型对数据样本集进行拟合回归；以拟合回归函数作为适应度函数，进行粒子群算法寻优，得到磁钢参数最优值，并通过了仿真验证。结果表明：通过GPR-PSO模型的方法，可以有效的降低永磁同步电动机的气隙磁密波形的谐波畸变率，使波形有所改善。

[1] 蔡黎明. 永磁同步电动机电磁振动与噪声的研究[D]. 广东工业大学, 2016.

[2] 王灵敏. 永磁同步电机在输煤系统的应用可行性分析[C]// 长三角能源论坛,2015.

[3] 余家俊. 电动汽车用永磁同步电机控制算法应用研究[D]. 广东工业大学, 2013.

[4] 范坚坚, 吴建华, 黎宪林,等. 永磁同步电动机磁钢的多目标微粒群算法优化[J]. 电机与控制学报, 2009, 13(2):173-178.

[5] 谭建成. 永磁无刷直流电机技术[M]. 北京：机械工业出版社, 2011.

[6] 徐英雷, 李群湛, 王涛. 永磁同步电机空载气隙磁密波形优化[J]. 西南交通大学学报, 2009, 44(4):513-516.

[7] 刘景辉, 黄开胜, 陈治宇. 不同极槽配合对永磁同步电动机性能的影响[C]// 小功率电机学术交流会，2014.

[8] 吴苏敏, 董立威, 刘洋,等. 基于气隙磁密波形优化的永磁同步电机结构[J]. 电机与控制应用, 2014, 41(3):12-16.

[9] 范乐, 任宁宁, 郝萍,等. 基于Magnet的永磁同步发电机设计[J].微特电机, 2014, 42(2):26-28.

[10] 任江洪, 陈韬, 曹长修. 混合高斯过程回归模型在铁水硅含量预报中的应用[J]. 重庆大学学报, 2012, 35(2):123-127.

[11] 孙晓丹, 李新会, 石伟民,等. 基于粒子群优化算法的高斯混合模型和高斯混合回归用于橄榄油品质分析[J]. 平顶山学院学报, 2015(5):57-60.

[12] 乔少杰, 金琨, 韩楠,等. 一种基于高斯混合模型的轨迹预测算法[J]. 软件学报, 2015, 26(5):1048-1063.

[13] 杨维, 李歧强. 粒子群优化算法综述[J]. 中国工程科学, 2004, 6(5):87-94.

[14] 王小川. Matlab神经网络43个案例分析[M]. 北京：北京航空航天大学出版社, 2013.

Air-gapFluxDensityWaveformOptimizationofPermanentMagnetSynchronousMotorBasedonGPR-PSOModel

DuXiaobinandDengJianhua

(Guangdong University of Technology，Guangzhou 510006，China)

In order to obtain good sinusoidal waveform of air-gap flux density of permanent magnet synchronous motor, this paper takes harmonic distortion rate of axial air-gap flux density waveform as a target to optimize factor variables such as eccentric distance, pole-arc coefficient, thickness and magnetization direction of magnetic steel. The orthogonal experiment design method is introduced to rationally arrange the collocation of experimental factor variables. The simulation analysis is carried out by ANSYS Maxwell 2D finite-element software to get the data sample set. The data sample sets are fitted by Gaussian process regression (GPR) to obtain the fitted regression model. Variance analysis method is adopted to analyze the influence degree of various factors on harmonic distortion rate. Taking the fitted regression function as the fitness function, the particle swarm optimization (PSO) is used to find optimal magnetic steel parameters. Taking a 48-slot 8-pole permanent magnet synchronous motor as an example, the simulation experiment is carried out. The simulation result shows that GPR-PSO algorithm can effectively reduce distortion rate of air-gap flux density waveform of permanent magnet synchronous motor and well improve the waveform.

Harmonic distortion rate；orthogonal design；Gaussian process regression model；particle swarm optimization

10.3969/J.ISSN.1008-7281.2017.06.06

TM351

A

1008-7281(2017)06-0020-005

杜晓彬男1991年生；在读硕士研究生，研究方向为新型特种电机设计及其控制.

2017-04-24