基于全相位FFT的频率估计及其FPGA实现

苏俊亚，张霞

(中国传媒大学 理工学部，北京 100024)

基于全相位FFT的频率估计及其FPGA实现

苏俊亚，张霞

(中国传媒大学 理工学部，北京 100024)

信号截断会引起频谱的泄露，导致频率测量出现偏差。相对于传统FFT，全相位FFT能够抑制频谱泄露。本文针对一种谐振式红外传感器，首先对检测信号进行全相位FFT，然后利用传统FFT的频谱对全相位FFT的频谱进行校正，实现对频率的精确估计。将此测频方法在FPGA上进行硬件综合，利用Verilog HDL 语言，设计了频率测量电路。然后对所设计的频率测量电路进行仿真，仿真结果显示该方法在使用单精度浮点数进行运算时在MHz量级上可分辨1Hz的信号频率。

全相位FFT；相位差；FPGA；Modelsim仿真

1 引言

频率测量是众多电子技术中的一种基本技术[1]，在通信、导航系统、空间科学计算等领域有着广泛的应用。对于频率的测量，可以将时域信号进行FFT，然后在频域对信号频率进行估计，原始的信号序列较长，信号处理设备处理的长度有限，在进行FFT变换之前需对信号进行截断，导致了信号的频谱泄露。为了抑制信号频谱泄露，通常情况下可以对信号进行加窗，如汉宁窗、凯泽窗、布莱克曼窗等，这些窗函数的傅里叶频谱的第一旁瓣衰减大于矩形窗[2]，但是主瓣宽度也大于矩形窗，加窗处理在抑制旁瓣泄露的同时会出现主瓣模糊的问题，因此加窗处理不能较好地解决频谱泄露的问题，导致频率测量的精度不高。

针对以上问题，文献[3]提出了一种数字信号处理的新方法，即全相位快速傅里叶变换(all phase Fast Fourier Transformation，apFFT)，这种信号处理的方法在抑制频谱泄露的同时，不会导致主瓣模糊的问题。文献[4]提出了利用传统FFT的频谱对apFFT的频谱进行校正的方法，即FFT/apFFT综合相位差校正法，该校正法提高了频率测量精度。本文针对一种谐振式红外传感器[5]，将FFT/apFFT综合相位差校正法在FPGA上进行硬件综合，采用Verilog HDL 语言，利用开发软件提供的IP核，设计了频率测量电路。然后对所设计的频率测量电路使用Modelsim进行仿真，实现了对谐振式红外传感器频率的估计。

2 综合相位差校正法

FFT/apFFT综合相位差校正法[3]是对信号分别进行全相位FFT和传统FFT变换。全相位FFT是将采样的2N-1点数据经过预处理后得到N个数据，然后再进行传统的FFT。由于全相位FFT和传统FFT在齐次、叠加、时不变、频移等性质存在相似性，因此，可以采用传统FFT对全相位FFT的频谱进行校正。

在实际应用中，信号常为正弦或余弦信号，根据欧拉公式可知正弦和余弦信号由复指数信号经过线性叠加而得，因此只需研究复指数信号。一个幅值为A，初相位为θ的单频复指数信号可表示为

x(n)=Aej[w*(n-n0)+θ]n∈[0，N-1]

(1)

对其进行傅里叶变换，并对变换结果在wk=kΔw=2kπ/N上进行采样，可得其FFT频谱为

X(k)=Aej(θ-w*n0)2πδ(kΔw-w*)

(2)

窗函数序列为w(n)，n∈[0，N-1]，通常窗函数具有对称性，满足w(n)=w(N-1-n)，其FFT谱为

W(k)=Wg(kΔw)e-jτkΔw

(3)

其中τ=(N-1)/2，对信号加窗后的FFT谱为

=Aej(θ-w*n0)δ(kΔw-w*)*Wg(kΔw)e-jτkΔw

=Aej(θ-w*n0)Wg[kΔw-w*]e-jτ(kΔw-w*)，k∈[0，N-1]

(4)

对(1)式中的x(n)进行前、后窗函数序列均为w(n)的双窗全相位FFT，变换后的频谱为[5]

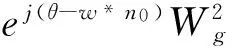
(5)

假设最大谱线所对应k值为k*，经过传统FFT的(4)式与经过全相位FFT的(5)式的相位谱差值为

Δφ=φx(k*)-φy(k*)

=[θ-w*n0-τ(k*Δw-w*)]-(θ-w*n0)

=-τ(k*Δw-w*)

(6)

由上式可得

w*=Δφ/τ+k*Δw，τ=(N-1)/2

(7)

从(7)式可看出只要求出两种谱线在主谱线上的相位差值Δφ，就可以得出信号频率的估计值。通过上述对FFT/apFFT综合相位差校正法的介绍，可得频率估计的流程如图1所示[6]。

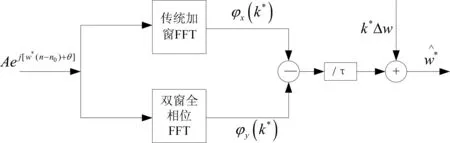
图1 基于FFT/apFFT综合相位差校正法的频率估计流程图

此频率估计方法包括传统加窗FFT和双窗全相位FFT，分别求出两者主谱线的相位值，其差值除以(N-1)/2可得频偏值，频偏值与主谱线的频率值相加后可得输入信号频率的估计值。FFT/apFFT综合相位差法与其他频谱校正方法相比，其综合了FFT和apFFT两者的优点，不但具有传统相位差法的所有性能，而且兼备了apFFT的频谱泄露小，可检测微弱信号的优点，其效率较高，性能较好[7]。

3 FPGA实现

选用Cyclone IV E系列的FPGA芯片不仅具有低成本、低功耗的优点，而且具有丰富的逻辑单元、I/O、存储器等资源，足以实现基于FFT/apFFT综合相位差校正法的频率测量方案；设计所用开发软件为QuartusⅡ14.1，该版本的软件设计了较多兼容Cyclone IV E 系列的IP核，利用这些已有的IP核进行设计缩短了开发时间；对于电路的仿真采用Modelsim SE 10.4，利用该版本可以更加快速实现系统的功能仿真；数据运算全部采用IEEE-754标准规定的单精度浮点数，与定点数运算相比，浮点数可以表示的数据范围更宽，计算的精度更高。FPGA开发过程中依据自顶而下、模块化的设计理念，图2是整体设计框图，进一步将分析每一模块电路，并使用Modelsim对其进行仿真，验证是否实现电路功能。

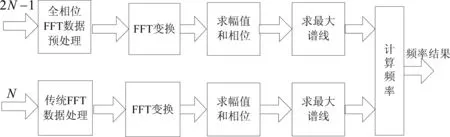
图2 FPGA设计整体框图

在全相位FFT数据预处理中，根据不同卷积窗函数可分为无窗全相位数据预处理、单窗全相位数据预处理和双窗全相位数据预处理，由图1可知此校正算法采用双窗全相位数据预处理。从主瓣宽度和旁瓣衰减幅度两方面考虑，双窗全相位数据预处理中的前窗函数和后窗函数均采用汉宁窗。在数据预处理中，使用MATLAB生成归一化的卷积窗序列，作为rom的初始化文件，加载到单端口rom中。整个数据预处理模块包括rom模块、乘法模块、fifo模块、reg_x0模块、加法模块、控制模块以及数据选择模块。其中控制模块为rom模块提供地址信号，为fifo模块和reg_x0模块提供读写使能信号，为数据选择模块提供选择使能信号，是数据预处理电路的核心模块，协调整个电路工作。图3是数据预处理模块的原理图。

传统FFT数据处理只需要将采样后的N点数据与N点窗函数序列相乘，相乘后的数据进行FFT变换即可。与全相位数据预处理相同，窗函数也选择汉宁窗，在MATLAB中生成汉宁窗序列，并经过编码变为单精度浮点数的数据形式，将其存储为MIF格式的文件，作为FPGA中rom的初始化文件，加载到单端口rom中，与输入未知信号进行运算。传统FFT数据处理模块包含三个模块，control模块、rom模块和mult模块。control模块控制rom模块的地址，地址每变换一次，rom会输出一个窗函数数据，rom的输出会延迟一个时钟，在testbench中控制未知信号的输入时间，与rom的输出保持一致，同步送入mult模块中，实现对未知信号的“加窗”处理。图4是传统FFT数据处理的原理图。

FFT变换模块采用Altera公司研发的FFT IP核，FFT v14.1可实现定点、单浮点、块浮点的FFT和IFFT运算[8]，变换的长度为2m(3≤m≤18)，数据流有流、变量流、缓存突发、突发四种结构。本次设计采用IEEE-754标准规定的单精度浮点数，此格式的数据位数为32位，FFT变换的长度选择1024点，数据流结构选择变量流。在对FFT核中各参数分析的基础上，将其进行配置，保存配置后即可自动生成Verilog VDL文件，将生成的文件加载到创建的工程中，即可在电路设计的过程中使用元件例化语句对生成的模块进行调用实现其功能。具体配置FFT核的参数如图5所示。

求幅值和相位模块的目的是求出FFT变换后输出复数的幅值和相位，运算的过程均采用单精度浮点数。在此模块中调用Quartus Ⅱ14.1中参数化模块库(LPM，Library of Parameterized Modules)里面的乘法、加法、除法和反正切模块，这些模块对Altera器件进行了优化，不耗用器件的逻辑单元，加快了设计的开发。求复数幅值采用乘法和加法模块实现运算，求复数的相位采用除法和反正切模块实现运算，反正切模块中角度的范围为-π/2～π/2，但是相位差校正算法中使用的角度范围为-π～π，因此必须采用校正方法对反正切模块输出结果进行校正，在代码中增加判断依据，具体的描述如下。

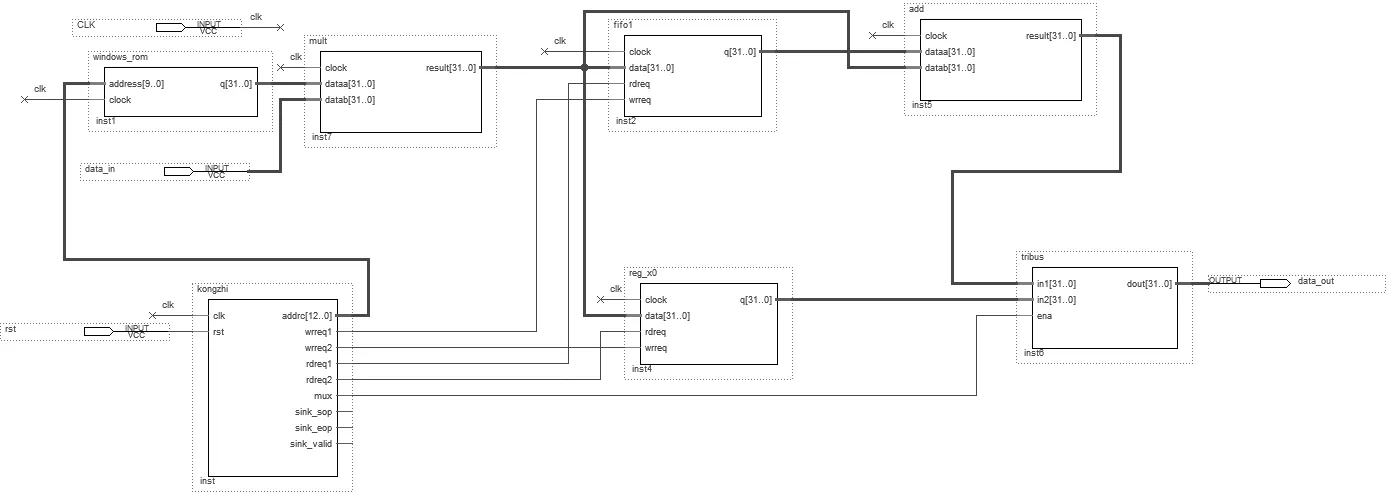
图3 全相位FFT数据预处理原理图

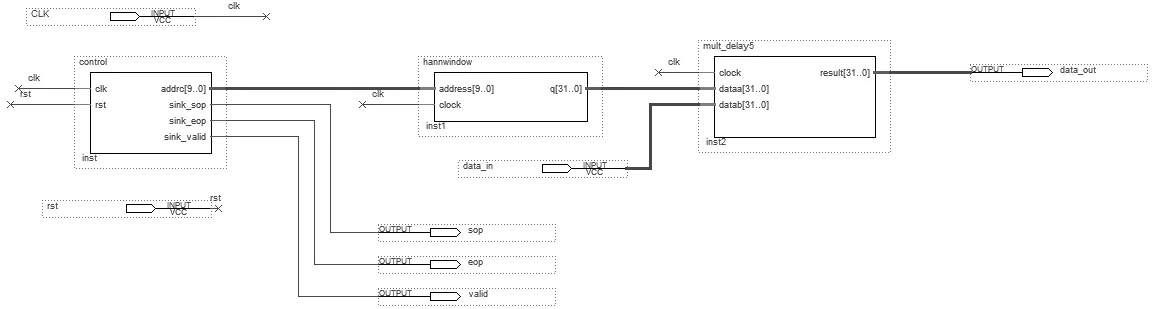
图4 传统FFT数据处理的原理图

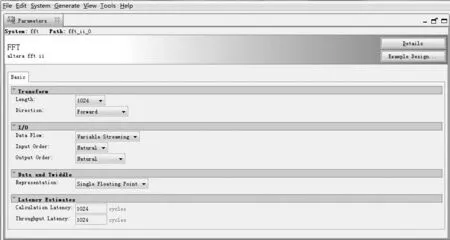
图5 FFT核的配置

(8)

在求幅值和相位模块中实现编号、幅值、相位三者同步后才能将结果输入到下一模块中进行运算，设计中采用触发器作为结果延迟单元，保证了结果同步输出。使用Modelsim对此模块进行仿真，仿真结果如图6所示，从图中可看出result_num、result_mod、result_phase同步，达到设计要求。

图6 求幅值和相位模块的仿真结果

求最大谱线模块中，只对输入的幅值信号进行比较，幅值信号是大于等于零的，因此可以设置一个初始值为零的临时变量与输入的第一个数据进行比较，每一个CLK输入一个数据，经过比较后将较大的数据放入临时变量中用于下一个时钟的比较。通过对全部幅值进行比较，求出最大幅值，并保存最大幅值所对应的相位值和编号值。求最大幅值的流程图见图7。使用Modelsim对此模块进行仿真，仿真结果如图8所示，从图中可以看出，经过幅值的不断比较后得到主谱线的编号值、幅度值和相位值。

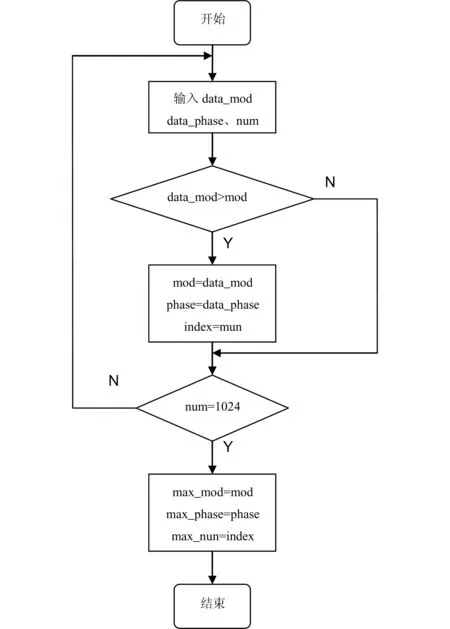
图7 求最大幅值的流程图

上述各个模块连接在一起可组成全相位FFT和传统FFT求主谱线相位值的电路设计。图9是全相位FFT求主谱线相位值电路设计的顶层原理

图8 求最大谱线模块的仿真结果

图，将未知信号的2N-1点采样数据送入到如图所示的电路中，经过数据的预处理，N点FFT变换，求出幅值和相位，然后求出主谱线所对应的幅度值、相位值和编号值。图10是传统FFT求主谱线相位值电路设计的顶层原理图，将未知信号中包含全相位FFT所需数据的第N点到第2N-1点采样数据送入图中所示电路中，经过“加窗”处理，N点FFT变换，求幅值和相位，然后求出经过普通FFT运算后主谱线的幅度值、相位值和编号值。

在计算频率模块中，全相位FFT和传统FFT的主谱线相位值和编号值作为此模块的输入数据，在此模块中首先计算传统FFT和全相位FFT主谱线的相位差值，然后除以(N-1)/2，最后与序列k值和fs/N的乘积进行加法运算，运算的结果是对未知信号频率的估计值。假设传统FFT主谱线对应的相位角度值为p1，全相位FFT主谱线对应相位角度值为p2，主谱线对应的编号为k，采样频率为fs，变换点数为N，则对未知信号频率的估计值为式9[9]。

图9 全相位FFT求主谱线相位值电路设计的顶层原理图

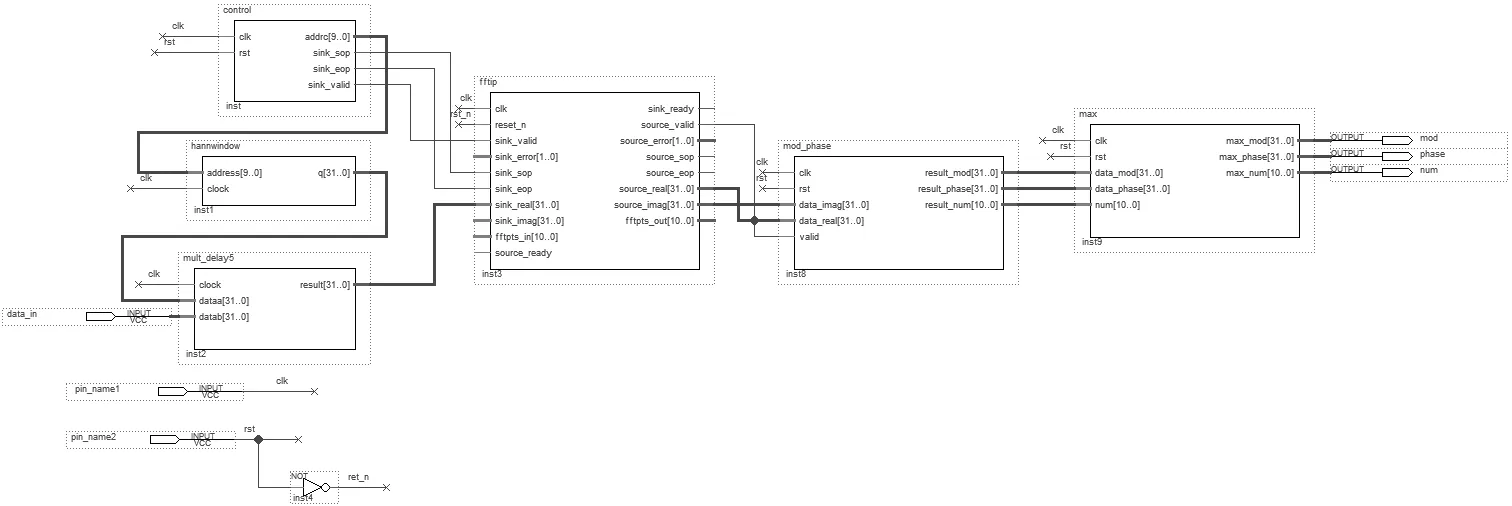
图10 传统FFT求主谱线相位值电路设计的顶层原理图

图11 计算频率模块的RTL视图

(9)

计算频率模块的RTL视图见图11。图12是当输入信号为4.5MHz时，使用Modelsim对此模块仿真的结果。从图中可以看出，设计的电路输出结果为未知信号的频率，实现了频率测量电路的功能。

图12 计算频率模块的仿真结果

4 仿真结果分析

本文所测量的谐振式红外传感器的固有频率约为4.5MHz，因此频率测试在4.5MHz左右展开。测试使用信号为正弦信号，初相位为零，采样频率为45MHz，进行1024点FFT变换；测试信号由MATLAB产生，并在MATLAB中转化成IEEE-754标准的单精度浮点数，写入文本文件作为电路设计输入。使用Modelsim对不同频率的输入信号进行仿真，仿真的结果如表1所示。

表1 频率测量电路仿真结果

从表中数据看出，仿真结果与实际信号频率相一致。本论文的频率测量是针对参考资料[5]的谐振式红外传感器固有频率进行检测，能够在MHz量级分辨1Hz即可满足要求。显然，仿真结果达到此要求。

5 结论

本文在FPGA上综合了FFT/apFFT综合相位差校正法，在综合算法过程中首先进行了全相位FFT变换，然后使用传统FFT对全相位FFT的频谱进行校正，校正后的频谱可得到频率值的精确估计。在FPGA硬件综合过程中使用了Quartus Ⅱ14.1提供的IP核，优化了设计，缩短了开发时间。FPGA开发是基于自顶而下、模块化的理念，使用Modelsim软件对设计的模块电路进行自下而上、层次化递加的功能仿真，最后对整个电路进行功能仿真，对仿真的结果分析可知，这种校正方法可以实现对谐振式红外传感器固有频率的测量。

[1]陈丽锋，孟瑞，冯希.频率测量研究综述[J].电力电子，2011(2)：50-53.

[2]周新星，王典洪.窗函数用于频谱分析的研究[J].软件时空，2009，25(12-3)：185.

[3]王兆华，黄翔东.数字信号全相位谱分析与滤波技术[M].北京：电子工业出版社，2009，63-69.

[4]黄翔东，王兆华.基于全相位频谱分析的相位差校正法[J].电子与信息学报，2008，30(2)：293-297.

[5]Xia Zhang，Dacheng Zhang.Thermal expansion mismatch resonant infrared sensor and array [J]. Optical Engineering，2015，54(8)：087102.

[6]王兆华，侯正信，苏飞.全相位FFT频谱分析[J].通信学报，2003，24(11A)：6-19.

[7]黄翔东.全相位数字信号处理[D]. 天津：天津大学，2006.

[8]刘东华.Altera系列FPGA芯片IP核详解[M].北京：电子工业出版社，2014.

[9]任丽棉.基于全相位FFT的高精度频率计系统研究[D].天津：天津大学，2009.

(责任编辑：宋金宝)

FrequencyEstimationBasedonFullPhaseFFTandItsImplementationonFPGA

SU Jun-ya，ZHANG Xia

(Faculty of Science and Technology，Communication University of China，Beijing 100024，China)

The signal cut off will cause a leakage of spectrum，resulting in frequency measurement deviation. Compared to the traditional FFT，all-phase FFT can inhibit the leakage of the spectrum. For a resonant infrared sensor in this paper，firstly，the full-phase FFT is performed for detection signal，and then conventional FFT can be used to correct the spectrum of the all-phase FFT to achieve the accurate estimation of frequency. This frequency measurement method is synthesized on the FPGA. Using the Verilog HDL language，a frequency measurement circuit is designed. Then，the frequency measurement circuit is simulated. By analyzing the simulation results，it is found that the method can distinguish the signal frequency of 1Hz around 4.5 MHz when single-precision floating-point is used to operation.

all-phase FFT；phase difference；FPGA；Modelsim simulation

TM935

A

1673-4793(2017)05-0050-07

2017-06-28

苏俊亚(1988-)，女(汉族)，河北邯郸人，中国传媒大学硕士研究生.E-mail：sujunya@cuc.edu.cn