基于声子晶体理论的无人机自动驾驶仪减振方法

孟 浩，高 永，李 冰，郭卫刚，康小伟，李本威

（海军航空大学，山东烟台264001）

基于声子晶体理论的无人机自动驾驶仪减振方法

孟 浩，高 永，李 冰，郭卫刚，康小伟，李本威

（海军航空大学，山东烟台264001）

将声子晶体理论引入无人机自动驾驶仪的减振设计。在此基础上，设计了局域共振减振板，并采用遗传算法对局域共振减振板的材料力学参数和结构参数进行了优化设计。仿真和实验测试结果表明，局域共振减振板对无人机自动驾驶仪具有较好的减振功能。

声子晶体；自动驾驶仪；减振

无人机具有无人员伤亡、隐蔽性好、效费比高、作战用途多、生存能力强，以及作战环境要求低等特点，在现代战争中的作用日渐突出，已经成为现代空中军事力量中的重要组成部分[1]。无人机也是信息战和网络中心战的重要装备之一，尤其是在近年来战争中的成功运用，也进一步证实了无人机在现代战争的地位。因此，世界各国广泛开展研究，无人机相关的科学技术得到迅猛发展。自动驾驶仪是无人机的核心部件之一，为保证其内部的IMU单元、加速度传感器等各种精密传感器的正常工作，通常需要安装在振动水平较低的舱段内。小型燃油动力的无人机通常采用单缸/双缸二冲程发动机，发动机作为一个振源，通过机体将振动传递到自动驾驶仪上，恶化了自动驾驶仪的工作环境。传统的减振方法通常采用隔振、动力吸振器等技术实现，但是由于结构复杂，附加重量过大的原因，不适合小型无人机自动驾驶仪的减振。声子晶体作为一种新型的减振材料，其“小尺寸控制大波长”的优点，为自动驾驶仪的减振技术提供了一种可能。

1 声子晶体理论简介

声子晶体概念通过类比光子晶体得出，人们在研究弹性波在周期弹性复合介质中传播时，偶然发现会产生类似于光子带隙的弹性波带隙，从而提出了声子晶体概念。在固体物理学领域，声子晶体主要是指弹性常数及密度周期分布的材料或结构，它是由弹性固体周期排列在另一种固体或流体介质中形成的一种新型功能材料[2]。

根据通带和带隙的定义，当弹性波在声子晶体中传播时，由于其内部结构的特殊性，带隙内的弹性波被阻止传播，而通带范围的弹性波可以无损耗地传播。声子晶体带隙产生的机理有2种：布拉格散射型和局域共振型[2]。布拉格散射型声子晶体起着主导作用的主要是结构的周期性，当入射弹性波的波长与结构的特征长度相近时，将被结构强烈散射耗散，从而形成带隙。而局域共振型声子晶体的带隙则主要是由单个散射体的共振特性起决定的。

1.1 布拉格散射声子晶体

布拉格散射声子晶体结构如图1所示。

对布拉格散射机理，已有大量文献进行了研究。当布拉格散射型声子晶体的基体为流体时，仅有纵波在基体中传播，带隙源于相邻原胞间的反射波的同相，其带隙特性表现为：第一带隙中心频率对应的弹性波波长约为晶格常数的2倍。当布拉格散射型声子晶体基体为固体时，内部同时存在纵波和横波，而且纵波和横波之间可以相互转化，其带隙特性表现为[3]：带隙频率对应的波长与横波波长处于同一数量级。影响布拉格散射型声子晶体带隙特性的因素主要包括组元材料的密度、弹性模量等物理参数，以及布拉格散射型声子晶的晶格形式、尺寸大小及填充率等结构参数[3-6]。

1.2 局域共振声子晶体

2000年，刘正猷在Science上最早提出局域共振型声子晶体的概念，其结构如图2所示，单个局域共振单元由硅橡胶包裹铅球构成，并按照简单立方晶格排列在环氧树脂基体中[5]。理论计算和实验测试都证实这种局域共振声子晶体结构尽管其单元特征长度仅20mm，但是其低频带隙低于400Hz。与相同尺寸的布拉格散射型声子晶体结构相比，第一带隙频率降低了近2个数量级。局域共振型声子晶体的这种低频特性引起了很多学者的关注和深入研究，局域共振的带隙机理和传输特性也逐渐清晰。研究表明，在局域共振结构中，中间包覆层与其他材料相比相对较软，芯体材质则相对较硬，芯体-包覆层-基体组成了具有低频的共振单元。当基体中弹性波频率与共振单元的共振频率接近时，局域共振结构单元将与弹性波发生强烈的耦合作用，在强耦合作用下，弹性波能量将被耗散，从而导致了带隙的产生[2-7]。

局域共振声子晶体的主要特点表现在以下4个方面[2-7]。

1）与相同晶格尺寸的布拉格声子晶体带隙频率相比，它具有“小尺寸控制大波长”的特点。

3）带隙范围由单个局域共振单元特性决定，并且与局域共振单元的排列方式无关。

4）带隙宽度随局域共振单元填充率的增加递增。

鉴于局域共振声子晶体结构优越的低频减振特性，本文拟采用局域共振声子晶体原理构建一块局域共振减振板，用于自动驾驶仪与机体之间的连接，利用局域共振声子晶体的对自动驾驶仪进行减振。

2 局域共振减振板设计

要实现对某一频段的减振功能，需要对局域共振减振板进行结构设计。然后，采用相应的优化方法对其参数进行优化设计，才能实现特定频段的减振功能。

2.1 局域共振减振板设计

本文采用的局域共振减振板是由多个局域共振单元组成周期复合结构。单个局域共振单元结构和整个结构如图3所示。其中：图3 a）是局域共振减振板俯视示意图，它由若干层局域共振单元构成，同一层的局域共振单元结构完全相同，不同层的局域共振单元结构可以相同也可以不同；图3 b）局域共振减振板侧视示意图，方格内是单个局域共振单元结构示意图，它由基体、包覆层和芯体组成，2个相邻局域共振单元之间的距离称为晶格常数。

2.2 参数优化

遗传算法是由美国Michigan大学的John H Holland教授和他的学生们首创，该算法源于对生物系统所进行的计算机模拟研究。遗传算法求解搜索方式不同于传统优化算法的单点搜索方法，其搜索始于若干个点组成的种群，种群中的每个点都是问题的一个解。遗传算法在计算过程中，种群质量随着选择、交叉、变异的进化过程逐步优化，通过若干代的选择，最终得到问题的最优解。遗传算法优点主要表现在以下方面：①采用并行多点搜索方式进行最优解求解，扩大了搜索范围，其并行性适合在并行计算机上进行大规模计算，提高了运算效率；②遗传算法依赖性条件少，仅需目标函数的信息，对其他信息无特殊要求；在搜索空间上，没有连续性、可微性的限制，适用范围相对较广；③遗传算法最突出的优势在于具有解决多目标优化问题的能力[8-13]。基于上述原因，遗传算法在声子晶体材料与周期复合结构优化中得到广泛应用[14-18]。本文采用遗传算对局域共振减振板材料的力学参数和结构参数进行优化。

组织体系不是组织结构，其实是组织能力平台，比如像华为的人力资源体系、IPD、I S体系等。为什么不叫组织结构而叫管理体系平台呢？因为战略运营体系、干部管理体系、审计体系、IPD研发体系、CRM客户关系管理体系、ISC供应链体系，等等，这些体系形成了一个组织的营盘，形成了一个依靠人但是不会过于依赖人的组织营盘。

2.2.1 目标函数

对于宽频带的减振性能优化问题来说，其目标是使既定频段的振动衰减最大。由于单目标函数容易陷入局部最优解，因而不能满足优化设计的需求，因此，为使各个频率下的振动衰减达到最大，必须采用多目标函数优化技术。在多目标函数进行优化时，需要考虑各个目标函数间的权重关系，如果各个目标函数的地位相同，最终目标函数则JRT可以采用平均加权方法得到：

一般，为保证安装精度和减轻飞机重量，局域共振减振板的密度和厚度有较为严格的限制。局域共振单元的结构形式也决定了其包覆层的外径应大于芯体半径。上述约束条件采用约束函数形式为：

式（2）中：为局域共振减振板的平均密度；h为局域共振减振板的厚度；ρc和hc为预先设置的参考数值；R1、R2为包覆层的外径；r1、r2为芯体的半径。

综合考虑上述约束条件，局域共振减振板在既定频带上的优化问题可以表述为：

使得hp(x)≤0，p=1,2,3,4。

hp(x)表示第p个约束条件。遗传算法在优化过程中需要将约束性优化问题转化为无约束性优化问题。本文采用惩罚函数来实现约束性问题向无约束性问题的转化。利用惩罚函数Hp[hp(x)]，本文的优化问题可以转化为非约束性的问题：

这里G表示遗传代数，惩罚函数为：

2.2.2 优化参数

局域共振减振板的优化变量主要涉及材料的力学参数，如基体和包覆层的杨氏模量、泊松比、损耗因子；以及单元的结构尺寸参数，如芯体的半径，包覆层的半径等，以及晶格常数。

优化变量x的搜索空间如为：与基体相关的变量以下标h表示——密度ρh为900～1 600 kg/m3，杨氏模量Eh为 20～400 MPa，泊松比σh为 0.25～0.44，损耗因子μh为0.1～1.0。下标1和2分别表示第1层和第2层中的局域共振单元，其参数优化范围相同——密度ρ1、ρ2分别为1 000～1 500 kg/m3，杨氏模量E1、E2分别为0.1～100 MPa，泊松比分别为σ1、σ2，0.23～0.41，损耗因子μ1、μ2分别为 0.1～0.3，芯体半径r1、r2分别为1.0～7.0mm，包覆层外径R1、R2分别为1.0～7.5mm。

3 结果与分析

3.1 优化结果

图4中，横坐标为遗传优化代数，纵坐标为每一代中各个频率下的振动衰减的最大值，即：

从图4中可以看出，目标函数优化在80代以后，计算结果开始收敛，这说明，采用遗传算法能够快速高效的对局域共振减振板的力学参数和结构参数进行优化。

采用遗传算法对各参数优化结果如表1所示。从表1中可看出，各个参数均在搜索空间中，并得到2种不同结构尺寸和材料参数的局域共振单元。

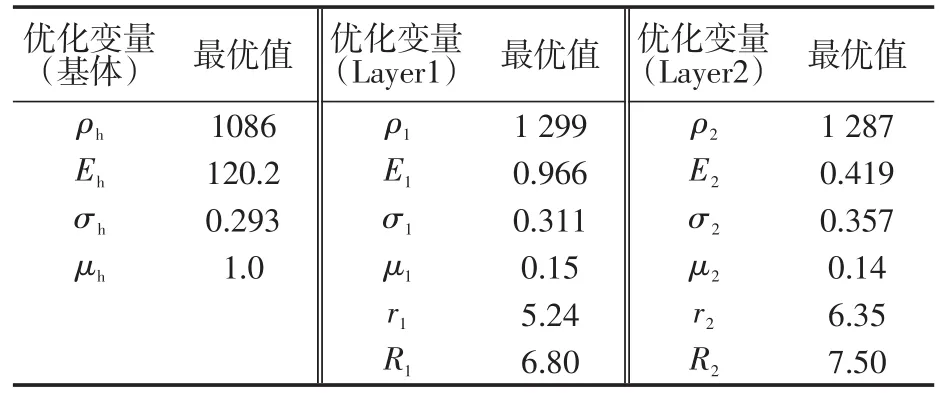
表1 优化后的材料参数Tab.1 Optimized material parameters

3.2 减振效果

3.2.1 仿真结果

采用商用软件Ansys对局域共振减振板进行建模仿真，仿真结果如图5所示。从图5中可以看出，在593～1 230Hz频段范围内的弯曲振动被抑制。

3.2.2 实验结果

将局域共振减振板与Pixhawk自动驾驶仪安装于无人机后，并在空中试飞。试飞后，通过Mission Planner提取飞参数据，结果如图6所示。

图6中，蓝色曲线为x轴加速度，红色曲线为y轴加速度，绿色为z轴加速度。从图6中看出，x、y方向的加速度数值在±5以内，z方向在±15以内，符合自动驾驶仪对振动环境的要求。

4 结论

本文将声子晶体理论引入无人机自动驾驶仪的减振设计中。在此基础上，设计了局域共振减振板，并采用遗传算法对局域共振减振板的材料力学参数和结构参数进行了优化设计。仿真和实验测试结果表明，局域共振减振板对无人机自动驾驶仪具有较好的减振功能。

[1]BELLINGHAM J，RICHARDS A，HOW J P.Receding horizon control of autonomous aerial vehicles[C]//Proceedings of American Control Conference.Anchorage，AK，2002：3741-3746.

[2]KUSHWAHA M S，HALEVI P.Band-gap engineering in periodic elastic composites[J].Applied Physics Letters，1994，64（9）：1085-1087.

[3]SIGALAS M M.Elastic wave band gaps and defect states in two-dimensional composites[J].Journal of the Acoustic Society ofAmerica，1997，101（3）：1256-1261.

[4]SIGALAS M M.Defect states of acoustic waves in a twodimensional lattice of solid cylinders[J].Journal of Applied Physics，1998，84（6）：3026-3030.

[5]LIU Z Y，CHAN C T，SHEN P，et al.Elastic wave scattering by periodic structures of spherical objects：theory and experiment[J].Physics Review B，2000，62（4）：2446-2457.

[6]RADE D A.Optimizations of dynamic vibration absorbers over a frequency bands[J].Mechanical Systems and Signal Processing，2000，14（5）：679-690.

[7]MOSHREFI TORBATI M.Passive vibration control of a satellite boom structure by geometric optimization using genetic algorithm[J].Journal of Sound and Vibration，2003（267）：879-892.

[8]PAUL G DYLEJKO，NICOLE KESSISSOGLOU.Optimization of a resonance changer to minimize the vibration transmission in marine vessels[J].Journal of Sound and Vibration，2007（300）：101-116.

[9]HE WC L，KANA D D.Four-pole parameters for imped-ance analysis of conical and cylindrical shells under axial excitations[J].Journal of the Acoustical Society of America，1968（43）：683-690.

[10]EL SABBAGH A，AKL W，BAZ A.Topology optimization of periodic mindlin plates[J].Finite Elements In Analysis and Design，2008，44（8）：439-449.

[11]OLHOFF N，DU J.Topology optimization of vibrating bimaterial structures with respect to sound radiation[C]//IUTAM Symposium on Topological Design Optimization of Structures，Machines and Materials：Status and Perspectives.Netherlands：SPRINGER，2006：43-52.

[12]JENSEN J S.Topology optimization problems for reflection and dissipation of elastic waves[J].Journal of Sound and Vibration，2007，301：319-340.

[13]GAZONAS G A，WEILE D S，WILDMAN R，et al.Genetic algorithm optimization of phononic band gap structures[J].International Journal of Solids and Structures，2006，43（18-19）：5851-5866.

[14]WILDMAN R A，GAZONAS G A.Genetic programming-based phononic bandgap structure design[R].Maryland：US.Army Research Laboratory，2011：118-119.

[15]LU L，YAMAMOTO T，OTOMORI M，et al.Topology optimization of an acoustic met material with negative bulk modulus using local resonance[J].Finite Elements inAnalysis and Design，2013，72：1-12.

[16]SY CHEN.An approach for impact structure optimization using the robust genetic algorithm[J].Finite Elements in Analysis and Design，2001，37（5）：431-446.

[17]HUSSEIN M I，EL BELTAGY M A.Optimization of phononic filters via genetic algorithms[J].Journal of Physics：Conference Series，2007，92：1-4.

[18]孟浩.局域共振声子晶体水声吸声材料吸声特性与设计技术研究[D].长沙：国防科技大学，2012：51-54.MENG HAO.Research on the performance and design technology og the underwater acoustic absorption materials of local resonance phononic crystals[D].Changsha：National University of Defense Technology，2012：51-54.（in Chinese）

Vibration Method of UAV Autopilot Based on Phononic Crystal Theory

MENG Hao,GAO Yong,LI Bing,GUO Weigang,KANG Xiaowei,LI Benwei
（Naval Aviation University,Yantai Shandong 264001,China）

The theory of phonon crystal was introduced into the design of vibration absorber for UAV autopilot.The local resonance vibration damper plate was design,and its structure and material parameters were optimized with genetic algorithm.The results of simulation and experiment showed that the local resonance damping plate had good vibration reduction function for the UAV autopilot.

phononic crystals;autopilot;vibration

V279；TB535+.1

A

1673-1522（2017）05-0438-05

10.7682/j.issn.1673-1522.2017.05.004

2017-02-14；

2017-07-22

“泰山学者”建设工程专项基金资助项目

孟 浩（1976-），男，讲师，博士。