基于新阈值函数的小波阈值去噪算法

卢广森， 黎 英， 毛 敏

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

基于新阈值函数的小波阈值去噪算法

卢广森， 黎 英， 毛 敏

(昆明理工大学信息工程与自动化学院，云南昆明650500)

小波基、分解层数、阈值和阈值函数是小波阈值去噪的关键性因素。针对小波基和分解层数的确定，提出了一个算法来实现；对于传统硬、软阈值函数的局限性和阈值函数在临界阈值处不存在平滑过渡区的现象，提出了一个参数化的新阈值函数，该阈值函数具有更高阶，通过灵活调节参数使之介于硬、软阈值函数之间，且兼具硬、软阈值函数的优点，并在临界阈值内添加平滑过渡区，可在阈值处理时保留一部分有用的高频信号，较好地抑制了细节系数的过扼杀和信号振荡现象。仿真结果表明：新阈值函数提高了去噪信号的信噪比，减小了均方误差，取得了较好的去噪效果。

小波变换； 去噪； 阈值； 阈值函数

0 引 言

小波变换在信号去噪领域中有着广泛的用途。目前，小波去噪方法大致可以分为三类：一是利用小波变换模极大值原理去噪；二是小波系数相关性去噪；三是小波阈值去噪。由于阈值去噪方法不仅实现简单，计算量较小，几乎能够完全抑制噪声，并且可以较好地保留能够反映原始信号的特征尖峰点，因此，小波阈值去噪是工程应用中最常用的信号去噪方法之一。阈值的选取规则是阈值去噪算法的关键。在常用的硬阈值和软阈值函数去噪处理中，硬阈值算法可以很好地保留信号边缘等局部特征，但处理过的小波系数在阈值处不连续，在信号重构时容易产生伪吉布斯(Pseudo-Gibbs)现象[1]；软阈值函数去噪算法处理相对平滑，但小波估计系数与含噪声信号的小波系数之间总是存在着恒定的偏差，直接影响重构信号和原始信号的逼近程度。为了解决硬阈值和软阈值存在的问题，学者提出介于硬、软阈值函数之间的Garrote阈值函数、半软阈值方法等方法[2～4]。文献[5]中提出的阈值函数介于硬、软阈值之间，改变函数参数也能够减小小波估计系数与含噪声信号的小波系数之间的恒定偏差，在整个小波空间域内，函数虽然连续，但是其高阶不可导，在临界阈值λ处曲线连续但不是平滑过渡的。

为了解决硬阈值的不连续性和软阈值造成的偏差问题，本文在文献[4]的基础上作出改进，提出了一个介于硬、软阈值之间的新阈值函数，该阈值函数具有高阶可导，且在噪声(小波系数)与有用信号(小波系数)之间存在一个平滑过渡区，改善阈值函数的连续性，进一步提高了信噪比，减小了均方误差，获得更好的去噪效果。

1 小波阈值去噪、阈值及阈值函数

小波阈值去噪的过程分为对含噪信号进行小波分解，高频系数的阈值量化处理和用小波逆变换实现信号重构3个步骤[6,7]。其基本原理如图1所示。

图1 小波阈值去噪原理

含噪信号经小波分解后，通常信号的系数要大于噪声的系数，选择一个合适的λ作为临界阈值，将小于该阈值的分解系数认为是由噪声引起的，予以舍弃；而大于该阈值的分解系数认为主要是由信号引起的，加以保留，即阈值去噪[8]。

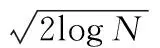
针对硬、软阈值函数具有一定的局限性，文献[5]提出了一种改进的阈值函数1如下

(1)

式中α为正数。阈值函数1介于硬阈值和软阈值之间，通过改变α能够减小估计小波系数与含噪信号的小波系数之间的恒定偏差，且有一定的函数连续性。在整个小波空间域内，函数虽然连续，但是其高阶不可导，在临界阈值λ处曲线连续但不是平滑过渡的。

2 新阈值函数的构建

针对硬阈值的不连续性、软阈值造成的偏差问题、阈值函数1不平滑过渡现象，提出了一种新的阈值函数。

新阈值函数

(2)

式中k和α为调节因子，且k和α为正数。

新阈值函数具有以下3个特征：

1)新阈值函数在定义域(-∞, +∞)内是连续的。

说明：新阈值函数的这种连续性，克服了硬阈值函数在阈值处的不连续性，同时也避免了因不连续导致的Pseudo-Gibbs现象。

2)新阈值函数在(-∞, -λ] 和 [+λ, +∞)定义域内的渐近线为硬阈值曲线。

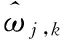
3)新阈值函数在(-∞, -λ]、 (-λ, +λ)和 [+λ, +∞)定义域内高阶可导。

证明：新阈值函数在(-∞, -λ] 、 (-λ, +λ)和 [+λ, +∞)定义域内是初等函数，根据初等函数的可导性质，可以知道，新阈值函数是一个高阶可导函数。

说明：新阈值函数的高阶可导性可以消除振荡现象，使重构信号显得平滑。

当k→∞时，新阈值函数为阈值函数1，在此条件下，当α→0时，新阈值函数为软阈值函数；当α→∞时，新阈值函数为硬阈值函数。因此，通过改变α值，新阈值函数可以在硬、软阈值之间灵活变化。新阈值函数在硬、软阈值之间，其参数k必须大于等于1，k决定了小波阈值的逼近程度，调节k使新阈值函数在阈值处理时能够保留一部分有用信号的高频部分，较好地抑制细节系数的过扼杀和信号振荡现象。

灵活调节k，α，新阈值函数曲线在硬、软阈值之间变化，如图2所示。

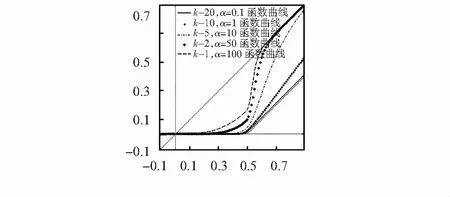
图2 不同k，α值时的新阈值函数曲线

3 小波基和分解层数的确定

小波基函数和分解层数的确定一定程度上决定去噪效果。分解层数过多，对各层小波空间系数进行阈值处理会造成信号的信息丢失严重，信噪比下降，且运算量大，处理变慢；分解层数过少，去噪效果不理想，信噪比不会下降，但是提高不多[12～14]。

对于小波基函数和分解层数的确定，提出了一个算法，能够对待处理的含噪信号进行分析，计算使用不同小波基函数对于含噪信号处理后的信噪比改善量，得出不同小波基函数与去噪信噪比改善量的关系，和分解层数与去噪信噪比改善量的关系，然后选择合适的小波基函数和最优的分解层数。

小波基函数的确定算法具体过程为：提供4种阈值选择方法(sqtwolog，rigrsure，heursure，minimaxi)，分解层数(1～10)和3种小波系(dbN，symN，coifN)；利用wden函数对给出的含噪信号进行去噪；由去噪后的信号和污染信号求出信噪比snr2；然后求差值snr2-snr1(注明：snr1为污染信号和原信号的信噪比)，循环改变阈值选取方式，分解层数和小波基函数，重复以上过程，得到差值矩阵；取差值矩阵每一行差值的最大值，构成新的一行，将构成的新的一行中的最大值赋给相应阶数的小波。过程如图3所示。

分解层数的确定算法具体过程为：基于小波基函数的确定，对污染信号使用wden函数进行去噪；去噪后得到的信号与原始信号进行信噪比计算得到snr2；求差值snr2-snr1(注明：snr1为污染信号和原信号的信噪比)依次改变分解层数，循环以上过程，最后得到一个差值序列；求差值序列中的最大值。过程如图4所示。

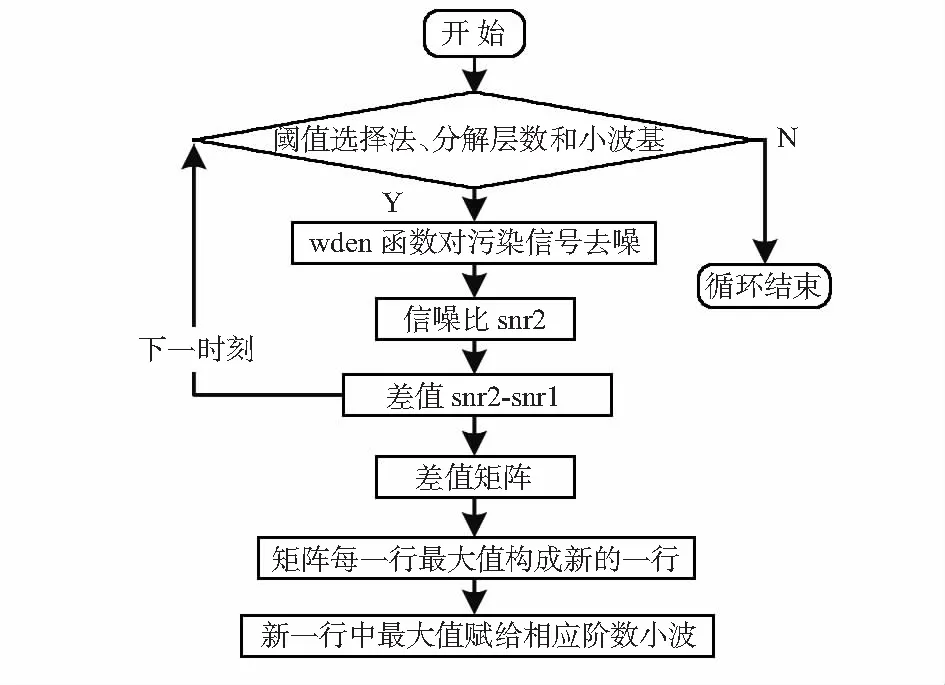
图3 不同小波基函数处理后信噪比改善量的流程

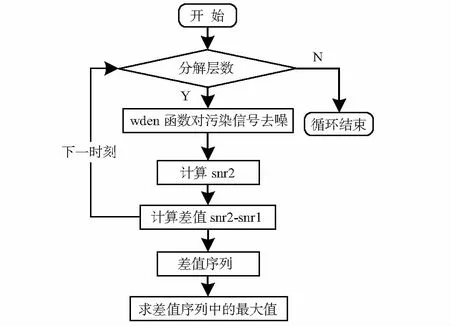
图4 不同分解层数对信噪比改善量的流程

4 仿真实验与分析

实验采用Matlab软件，选取用于测试小波去噪效果的典型测试数据Droppler，bumps信号，对其加入snr=10 dB的高斯白噪声，分别用传统的硬、软阈值和文献[4]中的阈值函数以及新阈值函数进行仿真。对于含噪Droppler信号，利用新算法实现小波基的确定，新算法运行结果：小波基函数及其信噪比改善量曲线，如图5所示。根据图5分析，本文选择5 dB小波作为处理含噪信号的小波基函数。

图5 不同小波基函数能达到的最大信噪比改善量

选取5 dB小波作为处理含噪信号的小波基函数，再利用分解层数的新算法，改变分解层数，仿真得由不同分解层数及其信噪比改善量形成的曲线，如图6所示。根据图6分析，选择小波分解的层数是5层。

图6 不同分解层数达到的最大信噪比改善量

小波基函数和分解层数确定后，对含噪Droppler信号进行小波阈值去噪，去噪后的波形如图 7所示。和处理Droppler信号的过程一样，对bumps信号加入SNR=10 dB的高斯白噪声，利用新算法选择合适的小波基函数sym4，利用新算法确定分解层数为4层，然后对bumps信号进行小波阈值去噪处理。

图7 Droppler信号去噪效果

含噪bumps信号去噪后的波形如图 8所示。Droppler信号和bumps信号经各阈值函数处理后的信噪比SNR和均方误差MSE数据如表1和表2所示。

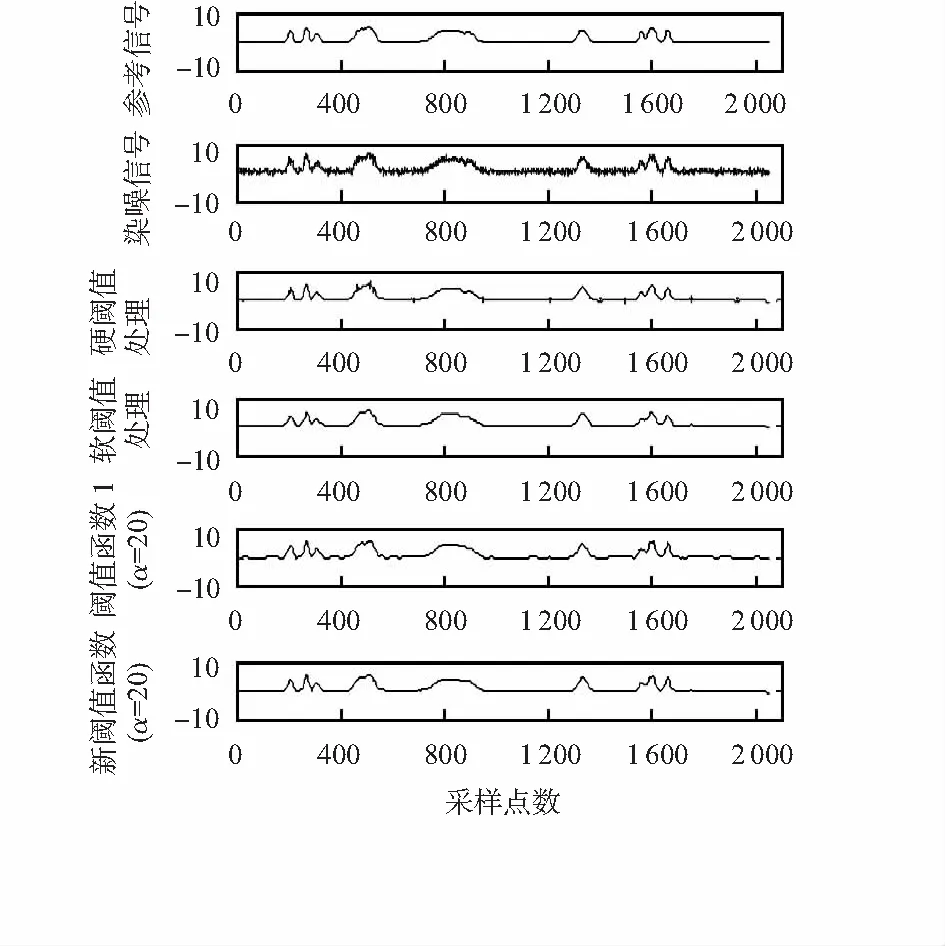
图8 bumps信号去噪效果

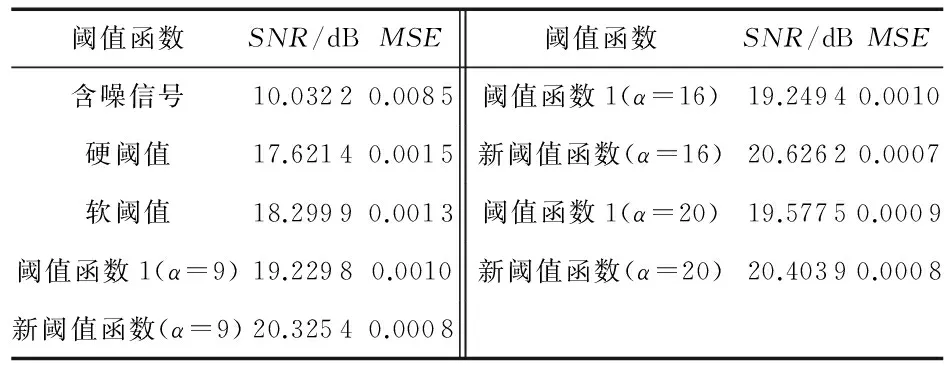
阈值函数SNR/dBMSE阈值函数SNR/dBMSE含噪信号10.03220.0085阈值函数1(α=16)19.24940.0010硬阈值17.62140.0015新阈值函数(α=16)20.62620.0007软阈值18.29990.0013阈值函数1(α=20)19.57750.0009阈值函数1(α=9)19.22980.0010新阈值函数(α=20)20.40390.0008新阈值函数(α=9)20.32540.0008

通过大量仿真实验，由结果分析如下：

1)含噪的Droppler和bumps信号经硬阈值函数去噪后，波形有一些振荡点分布，经软阈值函数去噪后，波形比较光滑。阈值函数1处理含噪信号后波形没有明显的振荡点且光滑，新阈值函数比阈值函数1处理后的波形更加光滑，没有附加振荡。同时对比信噪比和均方误差指标，新阈值函数比阈值函数1提高了SNR，同时进一步减小了MSE。研究表明：可以用SNR数值较大和MSE数值较小者作为评价去噪效果较好的规则。因此，无论从波形直观上或者从指标客观上均说明了新阈值函数去噪效果优于硬、软阈值和阈值函数1。

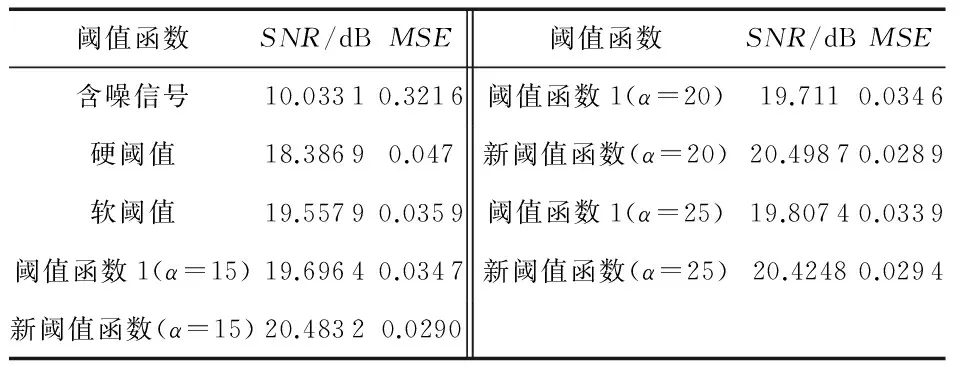
表2 各阈值函数对bumps信号去噪后的信噪比和均方误差

2)调节α值，使新阈值函数可以在硬、软阈值之间灵活变化。调节k值使新阈值函数在阈值处理时能够保留一部分有用信号的高频部分，较好地抑制细节系数的过扼杀和信号振荡现象。对于文中的含噪信号，当k=1时取得了较好去噪的效果。

3)对于小波基函数和分解层数的确定，提出的新算法起到了重要的作用。小波变换前的这种预处理计算速度快，同时算法简单，为去噪提供最佳的选择产生更优的效果。

5 结 论

针对硬阈值的不连续性、软阈值造成的偏差问题，提出了一种更高阶、平滑过渡的新阈值函数。仿真结果表明：相比于硬、软阈值函数和文献[6]提出的阈值函数1，新阈值函数在临界阈值内添加平滑过渡区，可在阈值处理时保留一部分有用的高频信号，较好地抑制了细节系数的过扼杀和信号振荡现象，进一步提高了去噪信号的信噪比，减小均方误差，获得较好的去噪效果。同时，针对具体的含噪信号，可以灵活调节阈值函数的k和α参数，满足不同信号处理的去噪要求，具有很高的实用价值。在仿真实验过程中，提出了一个新算法，完成小波基函数和分解层数的确定。针对具体的含噪信号，如何自动调整阈值函数的k和α参数，确定适合的小波基函数和分解层数，获得最佳的去噪效果，成为下一个研究目标。

[1] Li Huailiang,Tuo Xianguo,Shi Rui,et al.A de-noising algorithm to improve SNR of segmented gamma scanner for spectrum analysis[J].Nuclear Instruments and Methods in Physics Research Section A:Accelerators,Spectrometers,Detectors and Associated Equipment,2016,818:68-75.

[2] Bruce A G,Gao Hongye.Wave shrink with firm shrinkage[J].Statistica Sinica,1997,7(4):855-874.

[3] 韩 震,王红斌,余正涛.双边非局部均值滤波图像去噪算法[J].传感器与微系统,2016,35(6):124-127.

[4] 田 丰,孙 剑,邵 山，等.小波阈值去噪在传感器性能试验数据处理中的应用[J].传感器与微系统,2014,33(6):143-146.

[5] Zhang Xun,Li Juelong,Xing Jianchun,et al.A particle swarm optimization technique-based parametric wavelet thresholding function for signal de-noising[J].Circuits Syst Signal Process,2016,35(4):1-23.

[6] Hu Zhiqun,Liu Liping.Applications of wavelet analysis in diffe-rential propagation phase shift data de-noising[J].Advances in Atmospheric Sciences,2014,31(4):825-835.

[7] 王 琼，公丽颖，任伟建，等.基于改进小波阈值法的图像去噪方法[J].自动化技术与应用,2013,32(11):61-66.

[8] 黄一鹤.一种基于新的小波阈值函数的图像去噪方法[J].传感器与微系统,2011,30(9):76-78.

[9] Donoho D L.De-noising orthonormal redgelets and linear singua-larities[J].SIAM J Math Anal,2000,31(5):1062-1099.

[10] Kasambe P V,Rathod S S.VLSI wavelet based de-noising of PPG signal[J].Procedia Computer Science,2015,49:282-288.

[11] 单 锐,齐 越,刘 文.一种改进的小波阈值去噪算法[J].兰州理工大学学报,2014,40(4):101-104.

[12] Luciano C M Andrade,Mário Oleskovicz,Ricardo A S Fernandes.Adaptive threshold based on wavelet transform applied to the segmentation of single and combined power quality disturbances[J].Applied Soft Computing,2016,38:967-977.

[13] 田 丰,孙 剑,邵 山.小波阈值去噪在传感器性能试验数据处理中的应用[J].传感器与微系统,2014,33(6):143-146.

[14] Caio F F C Cunha,André T Carvalho,Mariane R Petraglia,et al.A new wavelet selection method for partial discharge de-noising[J].Electric Power Systems Research,2015,125:184-195.

Waveletthresholdde-noisingalgorithmbasedonnewthresholdfunction

LU Guang-sen, LI Ying, MAO Min

(CollegeofInformationEngineeringandAutomation,KunmingUniversityofScienceandTechnology,Kunming650500,China)

The wavelet basis,decomposition levels,threshold and threshold function are the key factors of wavelet threshold de-noising.An algorithm is proposed to realize the determination of wavelet basis and decomposition levels.Aiming at limitations of the traditional hard and soft threshold function and the phenomenon of no smooth transition in the critical threshold,the new parameterized threshold function is proposed.This new threshold function has higher order,with a smooth transition at a critical threshold,making it between hard and soft threshold functions through flexibly adjust parameters and possessing the advantages of both hard and soft threshold function.What’s more,it could retain part of some useful high frequency signal in threshold processing and effectively suppress the stifle of detail coefficients and the phenomenon of signal oscillation.Simulation results show that new threshold function improves the SNR of signal,reduces the MSE and obtains a better de-noising effect.

wavelet transform; de-noising; threshold; threshold function

10.13873/J.1000—9787(2017)12—0141—04

TN 911.7

A

1000—9787(2017)12—0141—04

2016—09—02

卢广森(1988-)，男，硕士研究生，主要研究方向为小波分析信号去噪。黎 英(1962-)，男，通讯作者，教授，主要从事电力电子技术及运动控制、嵌入式系统开发及其应用等方面的研究工作。