平面电容传感器参数优化设计及实验*

詹 争， 黄云志， 李 柯

(合肥工业大学 电气与自动化工程学院，安徽 合肥 230009)

平面电容传感器参数优化设计及实验*

詹 争， 黄云志， 李 柯

(合肥工业大学电气与自动化工程学院，安徽合肥230009)

平面电容传感器的性能指标由结构参数决定，如何优化结构参数使传感器达到良好的性能是传感器设计的关键。基于三维有限元仿真模型，研究了感应面积一定的条件下，电极对数、电极宽度与间距比对传感器信号强度、灵敏度及穿透深度的影响。采用神经网络方法优化结构参数，在保证穿透深度的条件下，获得较好的信号强度。研制了不同结构参数的PCB型平面电容传感器，并将其用于介电材料检测，实验结果证明了传感器参数优化测量的有效性。

平面电容传感器； 传感器性能； 结构参数优化

0 引 言

平面电容传感器是基于电容边缘效应的传感器，其电极位于同一平面，具有单边穿透、信号强度可调以及层析成像等优点[1]，且测量时对样本无任何损伤，与X射线、超声等无损检测技术相比，其成本低，效率高，具有广阔的应用前景。

传感器的结构参数有电极宽度、电极间距、电极厚度、电极对数、电极长度、基板厚度和基板介电常数[2]。传感器的结构参数决定其性能，研究结构参数对传感器性能指标的影响，有助于优化平面电容传感器的设计，提高传感器性能。

本文基于有限元三维仿真，在传感器感应面积一定的条件下，分析传感器电极对数，电极宽度与间距对传感器性能的综合影响，并给出优化的方法，研制传感器用于介电材料的测量。

1 平面电容传感器性能指标

传感器性能指标有信号强度、灵敏度和穿透深度。信号强度定义为传感器空载时输出电容大小。灵敏度取决于电容随被测样本的介电常数变化的程度

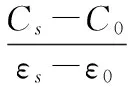
(1)

式中S为传感器的灵敏度；Cs为传感器在测量介电常数为εs时的输出电容；C0为传感器在测量空气时的输出电容；ε0为空气介电常数。灵敏度越大，输出电容值随样本介电常数的变化率越大，样本介电特性的改变则越容易被检测。

穿透深度为传感器电场能够穿透样本的理想高度，定义为[11]

(2)

式中Cγ=r为样本厚度为r时的互导电容值；Cmax为随着样本厚度增加得到的最大输出电容值；C0为传感器空测时的输出电容值。

2 平面电容传感器三维模型仿真

平面电容传感器如图1。

易非不知道田有园这句话里包含的到底是表扬还是讽刺，她什么也没说，沉默了半天，才问：“你说，我这么做对吗？我该怎么做？”

图1 平面电容传感器

传感器感应面积定义为A=[2(w+g)×N+w]×[L+w+g]。电极宽度、电极间距、电极对数和电极长度是影响传感器感应面积的主要参数。基于Ansoft Maxwell三维模型，在传感器感应面积一定的条件下，仿真电极宽度与间距比w/g、电极对数N对传感器信号强度、灵敏度和穿透深度的影响。仿真模型中，传感器感应面积均为20 mm×20 mm，电极均采用0.018 mm的铜厚，基板材料为FR4，介电常数为4.4，基板厚度为1.5 mm，样本相对介电常数εm为5，样本厚度0.1 mm，空气相对介电常数ε0为1。驱动电压给定1 V，感应电压给定0 V，仿真收敛误差设置为3 %。

由图2可知，传感器感应面积一定，随着电极对数、电极宽度与间距比值的增大，信号强度增大，灵敏度提高，而穿透深度降低。穿透深度决定了边缘电场能够穿透的样本厚度，信号强度越大，传感器信噪比越高。因此，如何选取合适的结构参数，取得信号强度和穿透深度的均衡，是结构参数设计的关键。

图2 感应面积一定时w/g及N对传感器性能指标的影响

3 优化设计

分析图2变化趋势，电极对数、电极宽度与间距比和信号强度、穿透深度之间均呈现非线性关系，考虑建立电极对数、电极宽度与间距比和性能指标之间的函数关系。神经网络具有以任意精度逼近任何非线性连续函数的能力，拟合精度高，具有良好的泛化效果。为了避免网络训练过程中出现过学习的现象，采用遗传算法优化的BP神经网络[12]分别建立信号强度、穿透深度和电极对数、电极宽度与间距比之间的函数关系，建立的网络模型如图3所示。

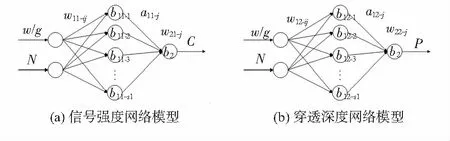
图3 信号强度和穿透深度网络模型

两个网络的建模方法，输入层输入电极宽度与间距比w/g和电极对数N，输出层分别输出信号强度C和穿透深度P，隐含层转移函数为tansig函数，输出层转移函数为线性函数。两个网络的输出可以表示为

(3)

式中w/g,N为网络输入，即电极宽度与电极间距比和电极对数;S1,S2为网络隐含层节点数;w11-1j,w12-1j,w11-2j,w12-2j为网络输入到隐含层的权值;b11-ij,b12-ij为隐含层阈值;w21-ij,w22-ij为隐含层到输出层的权值;b1,b2为输出层阈值;C,P为每个网络的输出，即信号强度和穿透深度。

采用上述100组仿真结果中的75组作为训练样本，25组作为预测样本，用遗传算法优化后的权值和阈值作为网络的初始权值和阈值。训练结束后，采用网络模型计算传感器的信号强度和穿透深度，与仿真值比较。信号强度误差绝对值在1 %以内，穿透深度误差绝对值在0.02 %以内， 考虑仿真设置的3 %收敛误差，模型求解的信号强度和穿透深度与仿真求解的信号强度和穿透深度基本吻合。

在传感器的实际测量中，为了保证传感器的电场集中在测量样本中，传感器的面积要小于等于测量样本的面积。在传感器感应面积一定的情况下，根据给定的信号强度和穿透深度指标要求，结合信号强度网络模型和穿透深度网络模型，即可获得满足要求的电极宽度与间距比和电极对数，达到信号强度和穿透深度的均衡。实际设计传感器，传感器信号强度也受硬件电路能测得的最小电容值的限制。

4 实 验

研制的不同结构参数的PCB型传感器如图4所示。

图4 PCB型平面电容传感器

传感器感应面积均为20 mm×20 mm，具体的结构参数如表1所示。

表1 5种传感器的结构参数

将研制的传感器分别接入LabVIEW测量系统，首先对传感器进行重复性误差标定[13]，测量频率范围为5～3 500 Hz，重复性误差均在0.05 pF以内。

采用研制的平面电容传感器对罗杰斯公司的RO3003型板材进行实验，板材的介电常数典型值为3，随温度和频率变化稳定，厚度为0.5 mm，两片板材叠加构成1 mm厚板材，感应面积均为25 mm×25 mm，可以完全覆盖传感器表面。为了减少误差，采用多次测量求平均值的方法。传感器对板材输出电容的扫频测量结果如图5所示。

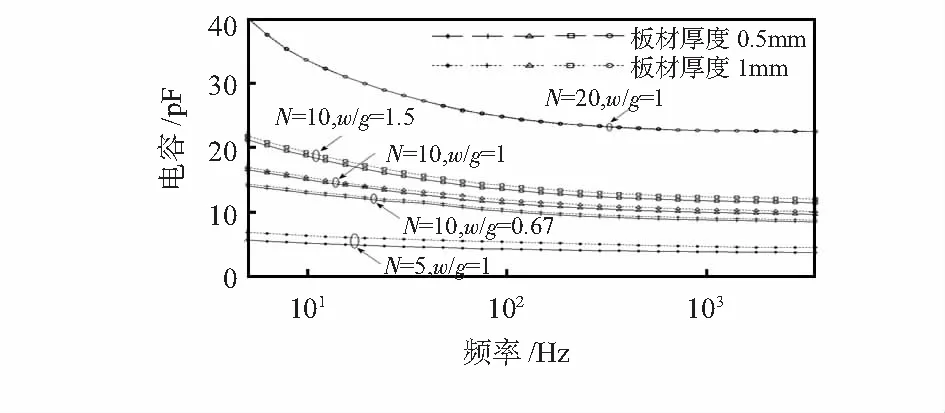
图5 扫频测量结果

由图5可知，扫频测量中电容随频率增加逐渐减小并趋向于稳定值。电极对数越大，电极宽度与间距比越大，输出电容越大。

以3 500 Hz频率处测量值分析，N=5,w/g=1传感器测得0.5和1 mm厚板材之间的电容差值最大，输出电容从3.734 4 pF增加到4.490 3 pF，输出电容增加了20 %；N=10,w/g=0.67传感器测量电容从8.461 5 pF增加到8.762 5 pF，输出电容增加了3.5 %；N=10,w/g=1传感器测量电容从9.643 1 pF增加到10.085 7 pF，输出电容增加了4 %；N=10,w/g=1.5 传感器测量电容从11.420 8 pF增加到12.023 7 pF，输出电容增加了5.2 %；N=20,w/g=1传感器测量电容值分别为22.509 4,22.527 1 pF，电容值基本不变。

由图2仿真结果可知:N=5,w/g=1传感器穿透深度在1.25 mm左右，可以穿透1 mm厚板材，板材越厚，测量电容值越大，因此,所测1 mm厚板材电容值相较0.5 mm厚板材电容值明显增大；N=10且w/g=0.67，N=10且w/g=1，N=10且w/g=1.5，传感器穿透深度在0.65 mm左右，在0.65 mm厚度范围内，板材越厚，测量电容值越大，因此，所测1 mm厚板材电容值相较0.5 mm厚板材电容值有所增加，但增加的幅度较小；N=20,w/g=1传感器穿透深度在0.35 mm左右，超出穿透深度的厚度对测量电容值基本无影响，因此，所测板材电容值基本不变。

综上所述，分别采用5种传感器对0.5 mm厚板材进行检测，N=5,w/g=1传感器能够穿透样本，但信号强度较小；N=20,w/g=1传感器信号强度最大，但不能完全穿透样本；N=10且w/g=0.67，N=10且w/g=1，N=10且w/g=1.5，传感器不仅能够穿透样本，而且信号强度依次增大。因此，N=10且w/g=1.5传感器是较为合理的选择。

5 结束语

本文基于有限元三维模型，在感应面积相同的情况下，研究了电极宽度与间距比和电极对数对性能指标的影响，随着电极对数、电极宽度与间距比的增大，信号强度增大，灵敏度提高，而穿透深度降低。利用遗传算法优化的神经网络建立性能指标与结构参数之间的模型，信号强度网络模型预测误差在1 %以内，穿透深度网络模型预测误差在0.02 %以内。研制了相同感应面积、不同结构参数的PCB型平面电容传感器，并将其用于板材测量。结果表明：优化的结构参数不仅能够保证穿透深度，而且信号强度较大。

[1] Hu X,Yang W.Planar capacitive sensors-designs and application-s[J].Sensor Review,2010,30(1):24-39.

[2] 汪蓓蓓，黄云志，刘永洪.平面电容传感器设计及在材料探伤中的应用研[J].传感技术学报，2014，27(7):997-1001.

[3] Li X B,Larson S D,Zyuzin A S,et al.Design principles for multichannel fringing electric field sensors[J].Sensors Journal,IEEE,2006,6(2):434-40.

[4] Nassr A A,Ahmed Wael H,El-Dakhakhni Wael W.Coplanar capacitance sensors for detecting water intrusion in composite structures[J].Meas Sci Technol,2008,19(7):075702.

[5] Syaifudin A M,Mukhopadhyay S,Yu P. Electromagnetic field computation using COMSOL multiphysics to evaluate the performance of novel interdigital sensors[C]∥Proceedings of the Applied Electromagnetics Conference(AEMC),2009:1-4.

[6] 张 欣,陈如山.人工神经网络和遗传算法在微带交指电容器设计中的应用[J].微波学报，2003，19(4):54-58.

[7] 李晓钰,姚 尧,谢 瑞.基于有限元的电容临近传感器研究[J].传感器与微系统，2010，29(8):51-53.

[8] 谢宁宁,陈向东,李晓钰.三电极平面电容传感器对材料损伤的检测[J].传感器与微系统，2011，30(4):57-62.

[9] 谢宁宁,陈向东,宋 濛.平面电容传感器在探测材料损伤中的研究[J].材料与器件，2011，36(7):497-515.

[10] 曹 河,董恩生,范作宪,等.同面多电极电容传感器结构仿真研究[J].传感器与微系统，2012，31(12):31-37.

[11] Kim CU,Li G,Li J,et al.Numerical analysis on effective electric field penetration depth for interdigital impedance sensor[C]∥The 7th International Conference on Applied Electrostatica,ICAES 2012,2012:012020.

[12] Wang Beibei,Huang Yunzhi,Zhan Zheng.Parameter estimation of multi-wavelength interdigital sensor based on optimized neural network[C]∥Proceeding of 2014 IEEE Interdigital Conference on Mechatronics and Automation(ICMA),2014:374-378.

[13] 黄云志，张慧凤，汪蓓蓓．多波长边缘电场传感器参数估计算法的研究[J]．传感技术学报，2013,32(1):63-66

Parametersoptimizationdesignandexperimentsofplanarcapacitivesensor*

ZHAN Zheng， HUANG Yun-zhi， LI Ke

(SchoolofElectricalEngineeringandAutomation,HefeiUniversityofTechnology,Hefei230009,China)

The performance indexes of coplanar capacitive sensor are determined by its structure parameters.It is very important for sensor design to optimize parameters.Based on three-dimensional finite element simulation model,effect of electrode width,electrode space ration and electrode numbers on signal strength,sensitivity,penetration depth is studied.The neural network is applied to optimize structure parameters,the signal strength is improved with the enough penetration depth.The sensors with different structure parameters are fabricated on PCB for dielectric material measurement.The experiments verify the effectivity of parameters optimization measurement.

planar capacitive sensor; sensor performance; structure parameters optimization

10.13873/J.1000—9787(2017)12—0095—03

TP 212

A

1000—9787(2017)12—0095—03

2016—06—03

安徽省科技计划资助项目(12010302059)；国家级大学生创新训练项目(201410359017)

詹 争(1989-)，男，硕士研究生，研究方向为计算机测控系统，E-mail:KacbsmZZ@163.com。黄云志(1976-)，女，教授，主要研究方向为传感器技术、数字信号处理和智能仪表，E-mail:hqyz@hfut.edu.cn。