基于自适应分解层数和阈值的小波去噪算法*
2017-12-08余本富王维博郑永康董蕊莹
余本富, 王维博, 郑永康, 董蕊莹
(1.西华大学 电气与电子信息学院,四川 成都 610039;2.国网四川省电力公司 电力科学研究院,四川 成都 610072)
基于自适应分解层数和阈值的小波去噪算法*
余本富1, 王维博1, 郑永康2, 董蕊莹1
(1.西华大学电气与电子信息学院,四川成都610039;2.国网四川省电力公司电力科学研究院,四川成都610072)
为了更好地降低电能质量扰动信号中的噪声,提出了一种基于自适应分解层数和阈值的小波去噪算法。通过计算小波细节系数的峰值比,自适应地确定最佳小波分解层数,根据各层细节系数中有用信息和噪声信息的分布特性以及细节系数的正、负峰值比,动态调整各层细节系数的上、下阈值。应用Matlab对暂态振荡和脉冲信号进行去噪处理,并与传统硬、软阈值算法和一种改进小波阈值算法相比。结果表明:本文提出的自适应分解层数和阈值的小波去噪算法得到的信噪比和均方根误差均优于以上3种方法,重构后信号更接近原始信号,并且较好地保留了扰动期间信号的特征信息。
小波去噪;自适应; 峰值比; 电能质量
0 引 言
电网中大功率开关的通断,以及电力线路和电力电子设备的投切,均会使电网中频繁出现尖峰干扰脉动信号和暂态振荡信号;严重影响电力系统的稳定运行[1]。但实际信号中,除了有用信息,还掺杂大量的噪声信息,严重影响信号特征的提取和识别,那么噪声的有效去除显得尤为重要[2]。
该领域出现了一些去噪方法,如数学形态学法、奇异值分解降噪法、基于经验模态分解(empirical mode decomposition,EMD)降噪法、小波去噪等[3~8]。目前国内外关于小波去噪方法的文献很多,如小波阈值去噪法、交叉验证法、自适应最佳分解层数等方法[6~9]。文献[10]结合小波系数的传播特性和噪声方差贡献率,对阈值进行改进,但去噪后造成了扰动期间部分特征信号的丢失。文献[11]采用改进小波阈值和分解层数的方法对磁共振波谱进行去噪。文献[12]提出了改进的阈值函数,并结合类切线寻优,去噪效果有所改善。
本文提出了一种基于自适应分解层数和阈值的小波去噪算法,基于Matlab产生暂态振荡和脉冲信号,添加不同强度的高斯白噪声,运用本文提出的方法进行去噪,并与硬、软阈值和文献[11]中的方法进行对比,更好地保留了扰动期间的特征信息,去噪后信号的信噪比(signal-to-noiseratio,SNR)和均方根误差(root mean square error,RMSE)优于以上3种方法。
1 传统的小波阈值去噪算法
假设一维非平稳、含噪声信号的数学模型为
x(t)=f(t)+ε(t)
(1)
式中x(t)为含噪信号;f(t)为原始信号;ε(t)为均方差为σ2的随机高斯白噪声。对x(t)进行离散小波变换
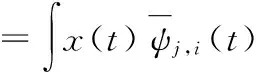
(2)
表示为
wj,i=uj,i+ej,i
(3)
式中ψj,i为离散小波;wj,i为x(t)的小波变换后各层小波系数;uj,i为f(t)的小波变换系数;ej,i为ε(t)的小波变换系数。
1.1 小波阈值函数去噪原理
小波阈值去噪可分为以下3个步骤:
1)小波分解含噪信号:选择合适的小波基和分解层数,对x(t)进行小波变换,得到wj,i;
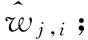
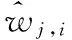
1.2 传统的阈值和阈值函数
硬、软阈值函数的表达式分别为
(4)
式中λ为给定的阈值。
(5)
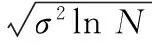
针对上述问题,本文所提算法根据细节系数峰值比自适应的确定最佳分解层数,通过细节系数分布特性和正、负峰值比计算出调节因子,动态调整上、下阈值。
2 自适应分解层数和小波阈值的去噪算法
2.1 自适应确定最佳小波分解层数
为了获得最佳小波分解层数k,根据细节系数峰值比自适应确定k值。暂态振荡信号和脉冲信号小波分解后的近似和细节系数如图1、图2所示。
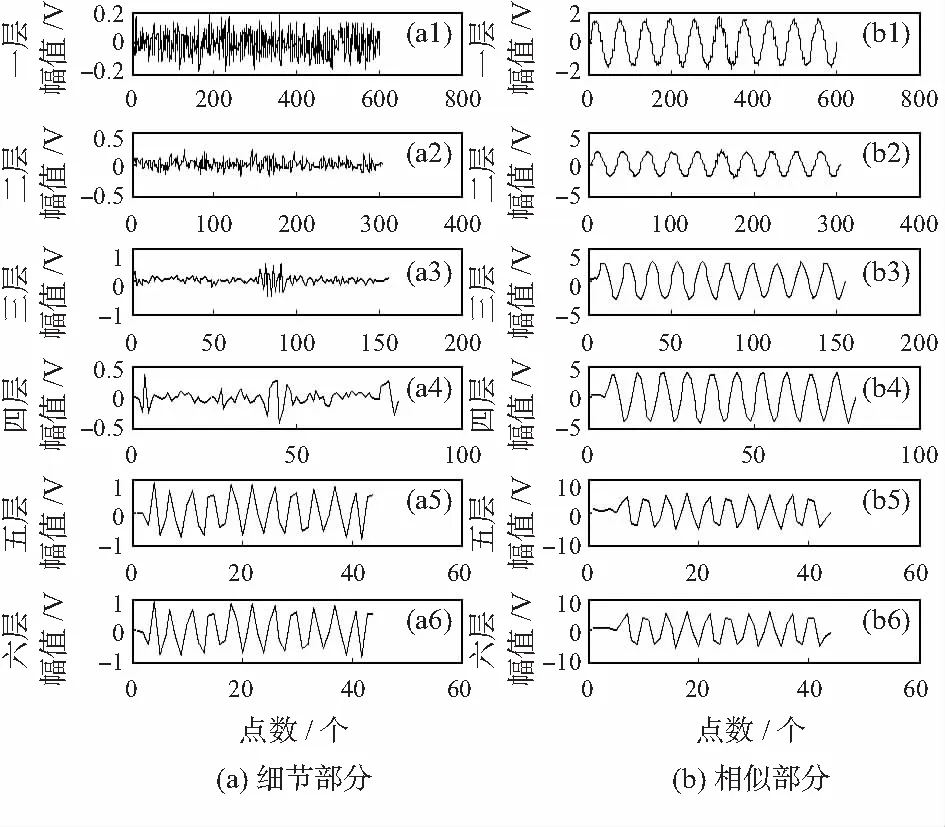
图1 振荡信号小波分解后细节和近似系数
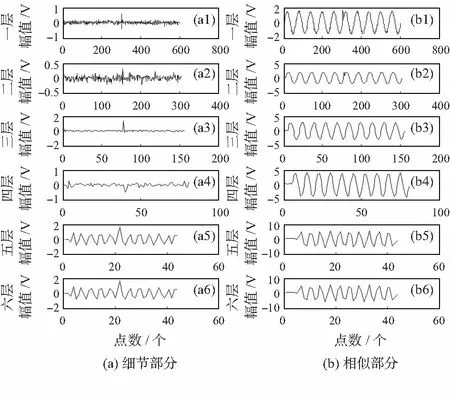
图2 脉冲信号小波分解后细节和近似系数
首先,定义第j层细节系数的峰值比
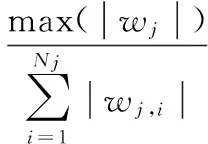
(6)
Sj可反映系数矩阵的稀疏程度,以及细节系数中有用信息和噪声信息含量的多少。
最佳分解层数的确定可参照以下4种情况实现:
1)细节系数中只包含噪声信息时,(如图1(a1));
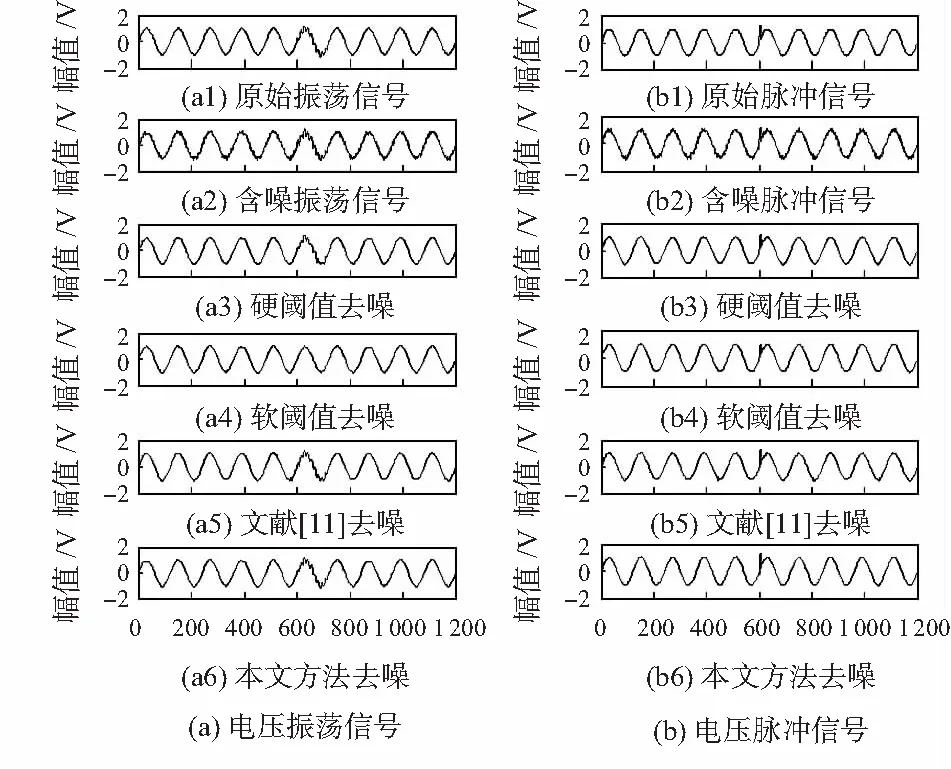
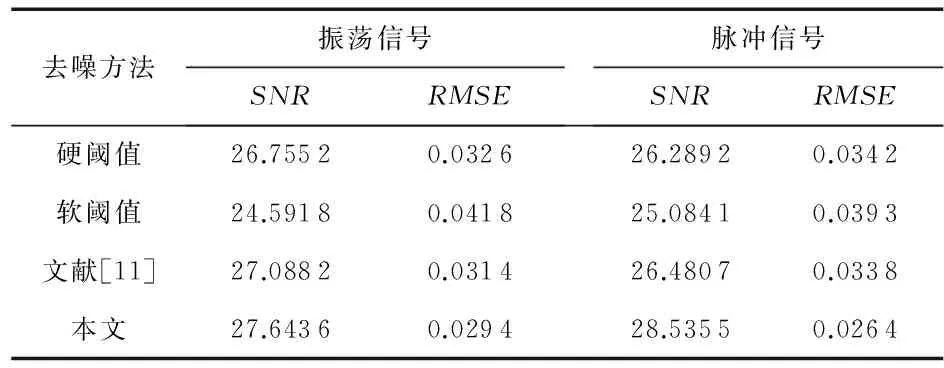
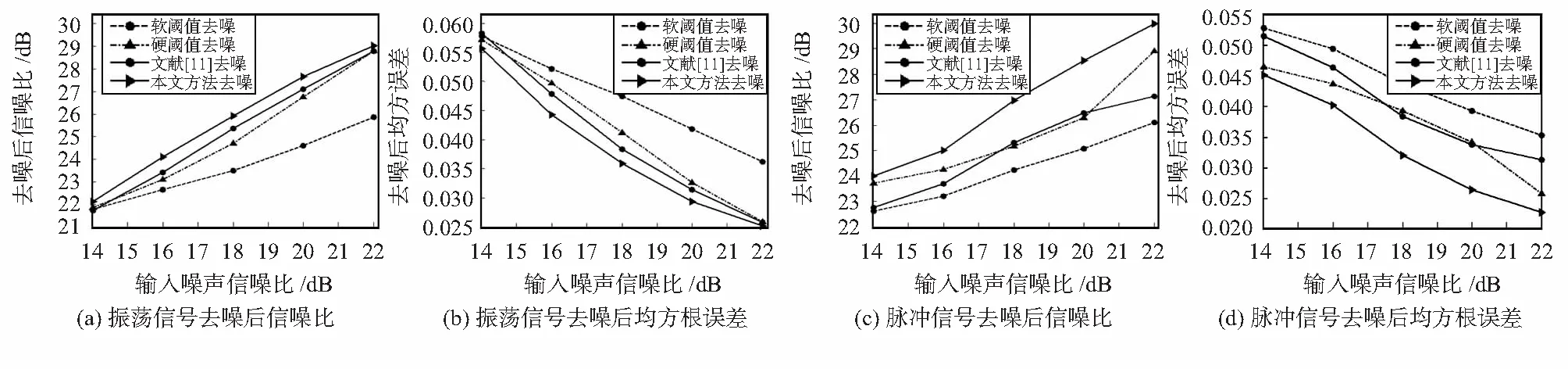
2)细节系数中包含大量噪声信息并含有少量幅值较大的有用信息时,0.01 3)细节系数中包含大量有用信息并含有少量幅值较小的噪声信息时,0.03 4)细节系数中只包含有用信息,不包含噪声信息时,Sj>Tr(如图1(a5)和(a6)、如图2(a5)和(a6))。 由情况(3)和(4)可知,Tr的数值可用来判断细节系数中是否含有噪声信息。因此,当满足Sj≤Tr和Sj+1>Tr时,最佳小波分解层数k的大小就等于j的数值。针对上述暂态振荡和脉冲信号,通过大量实验数据分析后得到,当Tr≈0.06时,能有效地区分某层细节系数中是否含有噪声信息。 目前,较为通用的固定阈值,自适应性差,并且随着信号长度N的增大,阈值明显偏大。因此,本文提出了自适应的上、下阈值计算公式 λj,L=μj-βj,Lδj (7) λj,H=μj+βj,Hδj (8) 式中λj,L和λj,H为第j层小波系数的下阈值和上阈值;βj,L和βj,H为第j层小波系数下、上阈值的调节因子;μj和δj为第j层小波系数的均值和标准差。 为了获得合适的βj,L和βj,H,首先计算上、下阈值调节因子的最大值 (9) (10) 式中 max(|wj<0|)为第j层小波系数负半轴最大峰值的绝对值;max(|wj>0|)为第j层小波系数正半轴最大峰值的绝对值。 与文献[11]不同,本文在运用峰值比Sj判定有用信息和噪声信息含量时,门限值不同;在处理含少量有用信息和大量有用信息的细节系数时,调节因子的计算方法也做了改进。那么各层细节系数的阈值调节因子计算方法如下: 1)小波分解后的各层细节系数中,当Sj≤0.01时,此时该层细节系数中只包含噪声信息,βj,L=βj,Lmax,βj,H=βj,Hmax,将该层的所有系数置零; 2)小波分解后的各层细节系数中,当0.01 3)小波分解后的各层细节系数中,当0.03 (11) (12) 式中Sj,L和Sj,H分别为负峰值比和正峰值比,表达式如下 (13) (14) 对于含大量有用信息的第j层小波系数,在求取该层小波系数的上、下阈值时,将该层小波系数分为正半轴系数和负半轴系数。(如式(13)、式(14)),可减少系数值的个数以及正、负半轴系数间的相互影响。 不同于其他阈值函数,硬阈值估计方法能较好地保留原始信号的某些尖锐特征,根据该特点,结合本文提出的上、下阈值对各层细节系数wj,i进行估计。本文所提算法的阈值函数表达式为 (15) 本文提出的自适应分解层数和阈值的小波去噪算法实现步骤如下: 1)选择合适的小波基,对含噪信号进行小波分解,得到第j层小波系数wj,i,j=1,2,3,…; 2)计算每层小波细节系数的峰值比Sj,自适应的确定最佳分解层数k,并令j=k; 3)根据第j层细节系数中有用信息和噪声信息的分布特性以及正、负峰值比,得到各层阈值的调节因子βj,L和βj,H,进而动态调整各层细节系数的上、下阈值λj,H和λj,L; 本文基于Matlab平台,利用电能质量扰动信号数学模型产生扰动信号。采样时间设为0.2 s,采样频率设为1 200 Hz,信号基频均为50 Hz。电压振荡信号模型为 x(t)=sinω0t+Ae-c(t-t2)sinβω0t· [ε(t-t1)-ε(t-t2)] (16) 式中ε(t)为阶跃函数;A为振荡幅度;β为振荡频率相对系数;c为振荡衰减系数;t2-t1为振荡持续时间。A和β取0.23 V,13.5;c和t2-t1取10,0.08 s。波形如图3(a)所示。 电压脉冲信号模型如下 x(t)=sinω0t+A[ε(t-t1)-ε(t-t2)] (17) 式中A为脉冲幅度;t2-t1为脉冲持续时间。两者分别取值1.1 V和0.000 6 s。波形如图3(b1)所示。 分别向上述两种暂态扰动信号中添加20 dB的高斯白噪声,得到含噪信号如图3(a2)和图3(b2)所示。分别采用硬阈值、软阈值、文献[11]和本文提出的算法对这2种含噪信号进行去噪处理。采用db 4小波基,依据小波细节系数的峰值比自适应确定分解层数k,4种方法去噪效果对比如图3所示,其中,横轴为采样点个数。 图3 电压振荡信号和脉冲信号去噪效果对比 从图3(a4)可以看出,软阈值去噪算法对于扰动期间的波形处理过于平滑,不能有效保留振荡信号扰动期间的特征,在采样点数为780~820时,本文所提算法明显优于硬阈值算法,较好地恢复了原始信号扰动期间的特征,失真现象明显小于软、硬阈值去噪法。从图3(b)可以看出,本文提出的算法去噪后的信号幅值要高于硬、软阈值和文献[11]去噪法,更接近原始信号,并且在突变点附近的曲线更平滑。 去噪性能优劣性的评价指标SNR和RMSE为 (18) (19) 表1 4种方法去噪后的信噪比和均方根误差 从表1的4组对比数据看出:本文方法对振荡和脉冲信号去噪后的SNR更大,RMSE更小,较硬、软阈值和文献[11]中的方法去噪效果更好;分别加入不同强度的高斯白噪声,4种方法去噪后信号的SNR和RMSE的数值对比曲线如图4所示。(表1和图4中数据均为重复进行100次试验求取的平均值) 从图4中的4组折线图对比看出:本文提出的方法相较于硬、软阈值和文献[11]的方法,去噪后获得的SNR和RMSE的数值最优。 图4 不同噪声强度下4种方法去噪效果对比 提出了一种基于自适应分解层数和阈值的小波去噪算法。通过计算每层细节系数的峰值比,自适应地确定最佳小波分解层数;根据细节系数中有用信息和噪声信息的分布特性以及正、负峰值比,得到自适应的上、下阈值,并且无需估计噪声标准差,再结合阈值函数对小波系数进行估计。针对暂态振荡和脉冲信号,分别采用硬阈值、软阈值、文献[11]和本文提出的方法对其进行去噪处理。相较于硬、软阈值去噪,本文方法更有效地保留了原始信号扰动期间的特征,并且在突变点附近的曲线更平滑。分别添加不同强度的高斯白噪声,从去噪后的SNR和RMSE折线图来看,本文提出的自适应方法始终保持SNR最大,RMSE最小,去噪效果明显优于其他3种方法。 [1] 张巧革,刘志刚,陈 刚.暂态振荡信号频率检测的Morlet小波谱峭度法[J].电力系统及其自动化学报,2013,25(5):1-6. [2] 钟金金.暂态电能质量信号的消噪、检测与识别研究[D].杭州:浙江工业大学,2011. [3] 赵 静,何正友,钱清泉.利用广义形态滤波与差分熵的电能质量扰动检测[J].中国电机工程学报,2009,29(7):121-127. [4] 胡卫红,舒 泓,栾宇光.基于奇异值分解的电能量信号去噪[J].电力系统保护与控制,2010,38(2):30-33. [5] 钱 勇,黄成军,陈 陈.基于经验模态分解的局部放电去噪方法[J].电力系统自动化,2005,29(12):53-56. [6] 田 丰,孙 剑,邵 山.小波阈值去噪在传感器性能试验数据处理中的应用[J].传感器与微系统,2014,33(6):143-146. [7] 张荣祥,李正强,郑世杰.基于遗传算法的双阈值小波去噪方法研究[J].传感器与微系统,2007,26(6):20-25. [8] 崔 治,李加升.基于小波熵自适应最佳分解层数确定算法[J].仪表技术与传感器,2015,37(6):127-130. [9] Johnstone L M,Silverman B W.Wavelet threshold estimators for data with correlated noise [J].Journal of the Royal Statistical Society,1997,59(2):319-351. [10] 邬春明,谢妮娜.改进的小波阈值在电能质量信号去噪中的应用[J].计算机工程与应用,2012,48(3):114-116. [11] Srivastava M,Anderson C L,Freed J H.A new wavelet denoising method for selecting decomposition levels and noise thresholds[J].IEEE Access,2016,4:3862-3877. [12] 袁开明,舒乃秋,孙云莲,等.基于阈值寻优法的小波去噪分析[J].武汉大学学报:工学版,2015,48(1):74-80. Waveletde-noisingalgorithmbasedonadaptivedecompositionnumberoflayersandthreshold* YU Ben-fu1, WANG Wei-bo1, ZHENG Yong-kang2, DONG Rui-ying1 (1.SchoolofElectricalandElectronicInformation,XihuaUniversity,Chengdu610039,China;2.StateGridSichuanElectricPowerInstitute,Chengdu610072,China) In order to reduce noise in electric energy quality disturbance signals,a wavelet de-noising algorithm based on adaptive decomposition level and threshold is proposed.The algorithm adaptively determine number of optimal wavelet decomposition levels by calculating peak-to-sum ratio of the wavelet detail coefficients and according to distribution characteristic of useful signals and the noise signals in detail coefficients of each levels and the ratio of peak value of the negative and positive of the detail coefficients,dynamically adjust upper and lower thresholds of the detail coefficients of each levels.The transient oscillation and pulse signals are de-noised by using Matlab,and compared with conventional hard,soft threshold algorithm and an improved wavelet threshold algorithm.The results show that number of adaptive decomposition level and the proposed threshold wavelet de-noising algorithm is superior to the other three methods in terms of signal-to-noise ratio(SNR) and root mean square error(RMSE) and the reconstructed signal is closer to the original signal,and better preserves the characteristic information of the signal during the disturbance period. wavelet de-noising;adaptive;ratio of peak values;electric energy quality 10.13873/J.1000—9787(2017)12—0126—04 TN 911.4 A 1000—9787(2017)12—0126—04 2017—01—21 国家自然科学基金资助项目(61571371);教育部“春晖计划”(Z2012026);四川省高校重点实验室开放基金资助项目(SZJJ2017—046);四川省电力公司课题(17209226);西华大学研究生创新基金资助项目(YCJJ2017165) 余本富(1991-),男,硕士研究生,主要研究方向为电能质量扰动检测。王维博(1977-),男,博士,副教授,主要研究领域为电能质量检测与分析、智能电网信息通信技术、智能优化算法,E—mail:wangweibo@mail.xhu.edu.cn。2.2 阈值选取
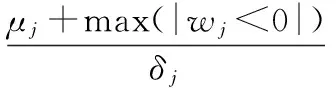
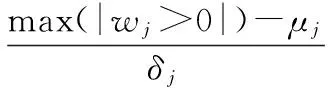
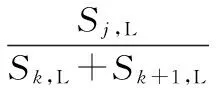
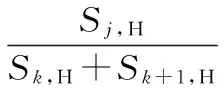
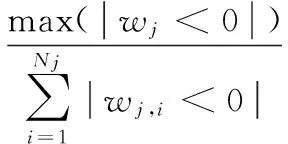
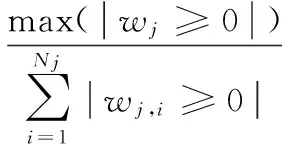
2.3 阈值函数确定
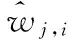
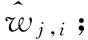
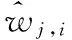
3 振荡信号和脉冲信号仿真分析
3.1 振荡信号和脉冲信号模型
3.2 振荡信号和脉冲信号去噪分析
3.3 4种方法去噪效果定量分析
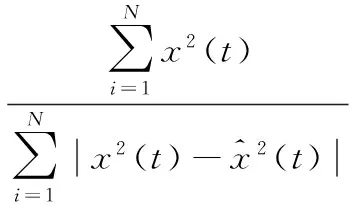
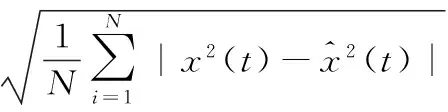
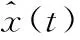
4 结 论
