基于单自由度共振反应的模态质量计算方法

黄国平，侯苏伟，王新忠

(1. 湖南城市学院 土木工程学院，湖南 益阳 413000；2. 北京建筑大学 土木与交通工程学院，北京 102616)

基于单自由度共振反应的模态质量计算方法

黄国平1，侯苏伟2，王新忠1

(1. 湖南城市学院 土木工程学院，湖南 益阳 413000；2. 北京建筑大学 土木与交通工程学院，北京 102616)

基于单自由度在简谐荷载下的共振响应结果反算单质点质量的思想，提出一种计算多自由度结构体系模态质量的方法，并利用MIDAS有限元软件求得模型模态质量，解决若干有限元软件不能直接提取模态质量的问题.模态质量原始公式计算结果与仿真实验结果的对比分析表明，该方法计算数值误差均小于5%，计算结果可以满足计算精度要求.

单自由度；共振响应；模态质量；有限元软件

多自由度结构的振动微分方程是一组二阶常系数线性非齐次微分方程组，在物理坐标系下，质量矩阵、刚度矩阵等均不可避免地会出现相互耦合，导致求解方程组较为复杂。通常的做法是对方程组进行解耦，亦即在振型坐标系下借助振型的正交特性使得质量矩阵和刚度矩阵转换为对角矩阵，将多自由度系统解耦成为多个单自由度系统，由此方程求解大为简化，该方法所谓振型分解法或振型叠加法[1-2]。得到的对角矩阵(刚度矩阵、质量矩阵)称为模态刚度阵、模态质量阵，简称为模态刚度(广义刚度)、模态质量(广义质量)。模态刚度和模态质量等都依赖于模态基坐标系，没有实际的物理意义，只具备数学计算功能。不过，在模态系下得到的该数学参量却是结构动力分析时重要的动特性参数。比如，在振动控制设计(如TMD设计)时需要提取模态质量，以此作为TMD系统质量设计的依据[3]。当前，研究结构振动问题普遍借助有限元分析软件进行求解，而有些软件程序往往又不能或不能直接获得模态质量等振动参数。为此，基于振型分解法及单自由度谐振反应，并依托MIDAS有限元软件，提出一种辅助软件获得模态质量的新方法。

1 单自由度谐振反应

众所周知，单自由度系统振动问题较多自由度简单，一般可以获得精确的解析解，但同时该体系却包括了结构动力分析中涉及的所有物理量及基本概念.因此先研究以单自由度振动体系在谐振荷载作用下的响应问题，若体系的物理3元素分别为质量m、刚度k、阻尼系数c，受到幅值为p0、角频率为ω的正弦谐振荷载p(t)作用，体系力学模型如图1所示，其运动方程为[4-5]

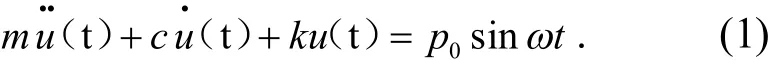
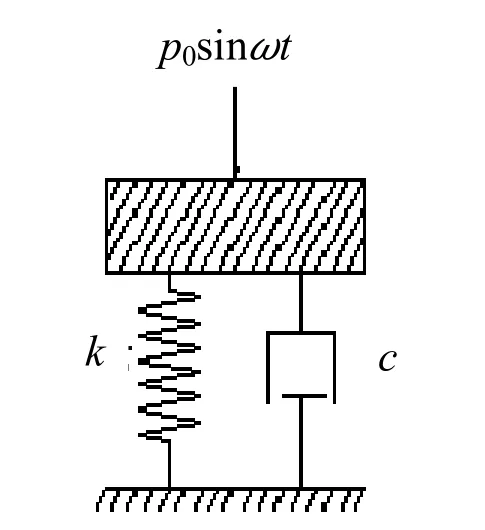
图1 弹簧―质点体系

由式(1)可求得单自由度质点受谐振荷载强迫振动的反应解析解为

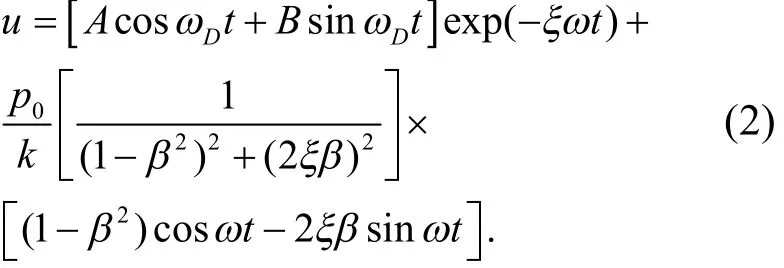
式(2)为运动方程的全解，其中第一项为瞬态反应u，即体系的自由振动反应uc，常量A、B给定的初始条件确定，由于exp(-ξωt)的存在瞬态反应很快随时间衰减而至消失.实际工程中往往关注其第二项稳态反应，该反应是由外荷载引起的强迫振动up，若只取稳态谐振反应则有

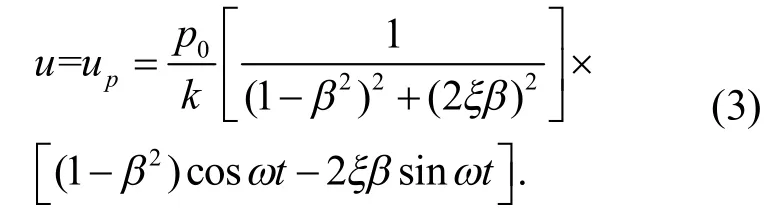
k为体系刚度有

结构动力学的研究内容和任务可分为2大类：一类是反应分析，输入动力荷载至结构系统，然后输出动力反应，为结构动力计算问题；另一类是通过输入的动力荷载和输出的动力反应反求结构系统，为参数(或称系统)识别问题.因此，按后者可根据输出的动力反应反算体系的质量，将(4)式代入(3)式并整理可得

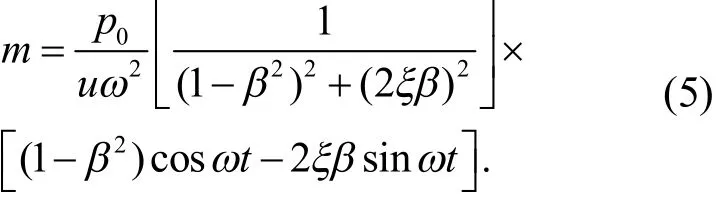
更为简便的，若谐荷载频率ω与体系体系频率ω相等时，即上式中β=1，让结构发生共振反应，则有

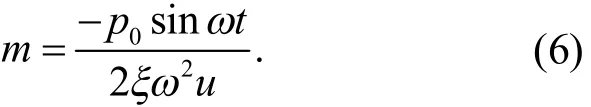
当输出最大位移反应(位移幅值)时(6)式可变为

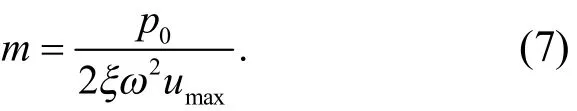
至此，可以根据体系共振时输出的位移幅值反应求得单自由度体系的质量.

2 振型分解与模态质量计算

更为一般地，工程结构往往离散为多自由度，仍可以建立振动体系的运动方程[4-5]如下：

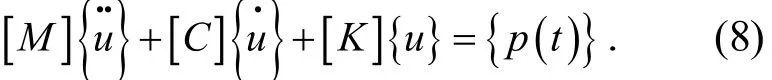
位移用振型

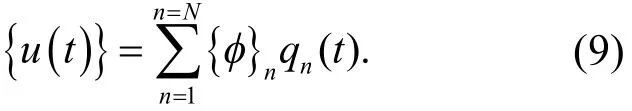
展开.式(9)代入式(8)得

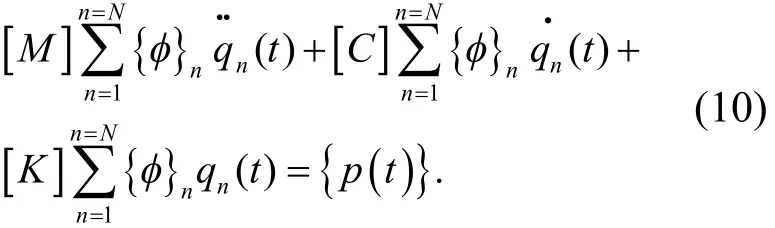
当满足阻尼阵[C]正交条件，式(10)左乘并利用振型正交性得

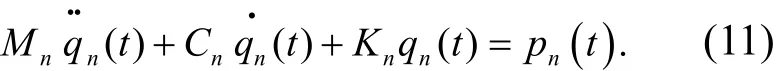
通过坐标转换将相互耦合的线性方程组式(8)分解为N个相互独立的方程组式(10)，物理意义为多自由度体系的振动问题在广义坐标下表现为N个单自由度体系的振动问题.对比式(1)、式(10)，形式完全一样，只是用Mn、Cn、Kn、pn及qn分别代替了m、c、k、p0sinωt和u.

目前工程结构的动力分析问题往往借助有限元软件程序完成，有时需要获得模态质量，而有些软件程序不能直接提取，若提取振型向量及质量矩阵后再用上述定义公式计算比较麻烦，对于庞大体系甚至是非常困难的.这样即可采用上述振型分解思想及单自由度谐振反应来间接求取模态质量.具体做法为：若要求得多自由度体系某阶模态下的模态质量，先建立有限元模型，进行模态分析，获取各阶自振频率，及个阶模态振型向量.当求某阶模态质量时，在某节点位置处施加一集中谐振荷载p0sinωt，必须说明的是此节点必须满足该阶模态振型向量在激振力作用方向不为0，最好是该向量值为较大或最大.其中ω为结构某阶自振频率，然后再进行谐振荷载时程分析，分析方法采用振型叠加法，程序计算得到响应结果是前n阶振型叠加后的发应，但注意到此时体系发生第n阶共振反应，前n-1阶反应贡献很小，n阶共振反应占主导，可近似认为总反应即为该第n阶模态的共振的反应，若为提高二者的接近程度，可通过人为设置合适阻尼实现，即前n-1阶振型阻尼取大值，n阶振型阻尼取小值的方法来抑制前n-1阶模态反应的贡献.需要说明的是，此时设置的振型阻尼是假定的，与实际结构阻尼情况并不相符，但对该数值方法求得模态质量并无影响.故由式(9)有

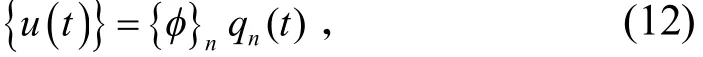
若只取j节点位移幅值反应则有

可得

将节点荷载转为模态坐标下的广义荷载有

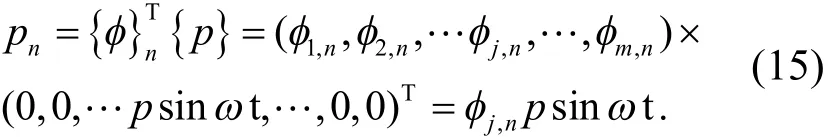
以Mn、pn及qn分别代替m、p0sinωt和umax后并将式(14)、式(15)代入式(7)得

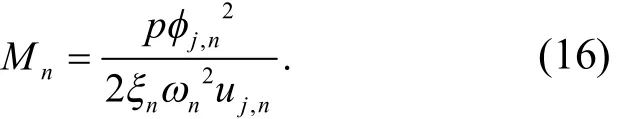
3 算例1：简支梁有限元模型

现以一简单的算例来说明上述方法来求得模态质量Mn.模型概况：简支梁，跨径l=10 m，截面面积A=1 m2，抗弯惯性矩Iyy=0.020 8 m4，材料弹性模量E=32 500 MPa，材料密度ρ=2.55 t/m3，建立MIDAS有限元模型如图2所示.

图2 简支梁有限元模型

先进行模态分析求得其动力特征参数频率及模态向量，分析前几阶模态振型特征，求取某模态质量时，以谐振荷载幅值p0，且频率为该阶自振频率的激励荷载作用于模态向量值较大处的节点处，作用方向与该模态向量一致，采用MIDAS软件计算谐荷载时程分析时，分析方法采用振型叠加法，阻尼计算方法采用振型阻尼，阻尼比ξ可取0.05，在后处理中提取激励荷载作用点及作用方向的节点位移反应幅值，即可运用式(16)求取该阶模态质量.现求取一阶模模态质量过程如下：在该阶模态向量最大值的位置处(如图2所示模型节点6)施加一集中正弦谐激励振荷载p(t)作用，激励荷载频率取结构一阶自振频率，取100 kN，频率取50.7 rad/sec，则p(t)=100sin50.7t；且只截取一阶模态进行计算，各节点的质量(软件可以直接提取，也可根据物理意义获得)、一阶模态向量及各点位移反应幅值列于表1.

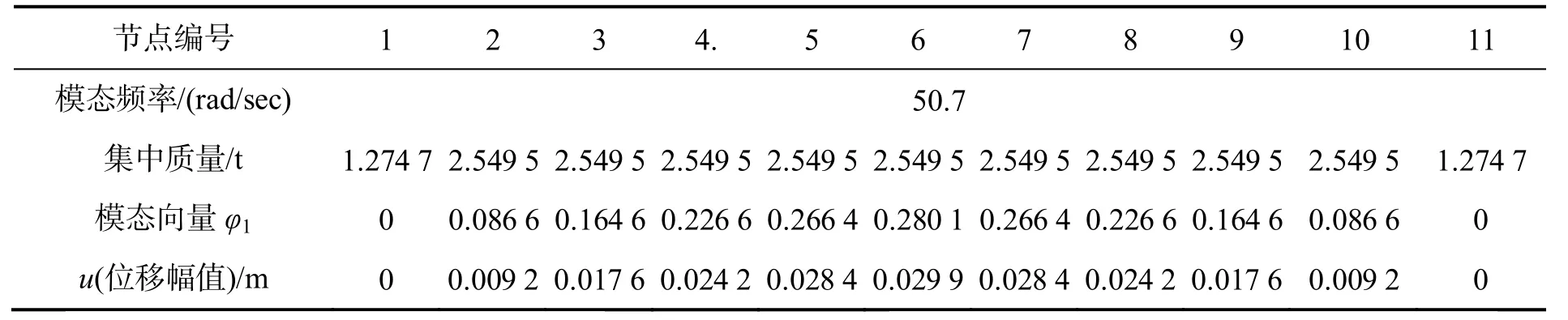
表1 模型一阶模态参数

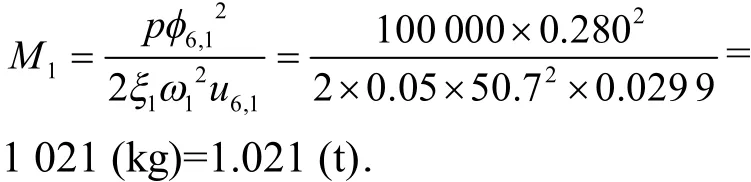
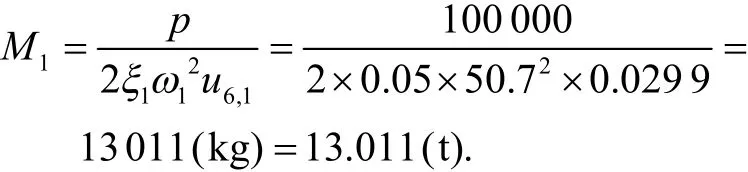
与分布参数体系解析解M1=m/2=12.75 t误差同样为2.1%.

表2为该简支梁模型前几阶模态质量的求解参数及计算结果，其中激励荷载Fz,6表示为荷载作用于6节点z方向，其他类同；所列模态向量及反应幅值均为荷载作用点处及作用方向的数值.同时考虑到有多阶模态叠加时，非共振模态的贡献，采用了不同振型阻尼设置的多种计算工况.计算结果表明：多阶模态叠加时采用该共振反应法所得结果精度高，非共振反应影响甚小，并且该数值计算模态质量的方法对假定结构的振型阻尼并不敏感.

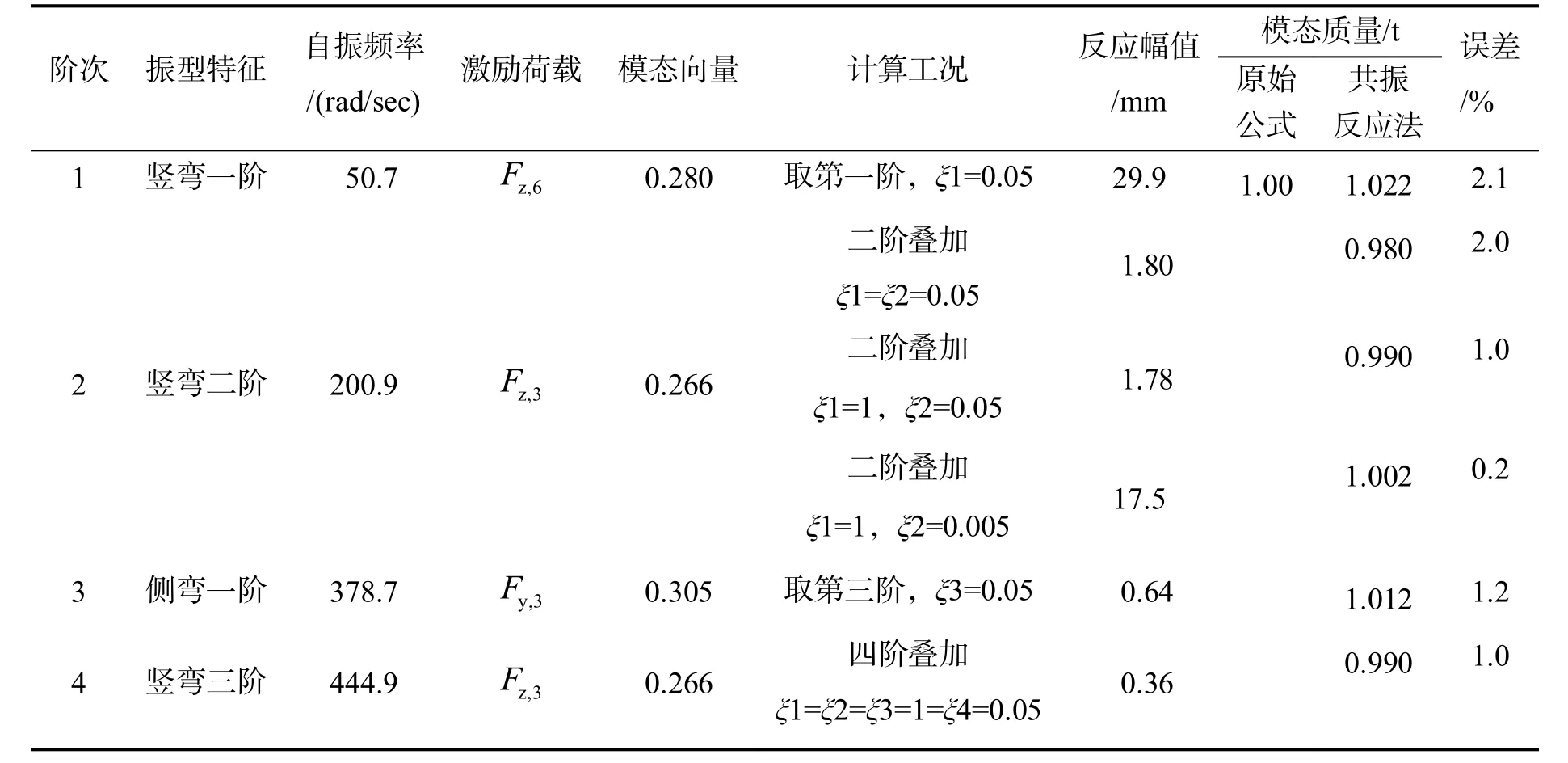
表2 简支梁模型低阶模态质量计算

4 算例2：弯桥有限元模型

在桥梁工程中，弯桥常应用于匝道桥、互通立交以及高速公路等，其结构受力较为复杂，主要特征表现为梁在承受竖向弯曲时，受曲率影响，必然产生扭转，即弯扭耦合作用[6].在弯桥动力分析时同样存在弯扭耦合模态，现以一实际弯桥模型为依托，说明该计算模态质量方法的有效性及适用性.

计算思路及步骤如算例1所述，首先建立起某弯桥有限元模型如图3所示，单元采用空间梁单元，模型节点编号始于弯桥桥面单元自左至右排列.其一阶模态的部分节点的振型向量如表3所列，可知，该弯桥第一阶模态的振型就出现了多向的偶联振动.

图3 某弯桥有限元模型

弯桥模型第一阶模态质量的求解参数及计算结果如表4所列，其中相关符号及数值含义与表2类同，在求取一阶模态质量时采用了不同的激励方式，计算表明：弯桥的藕联振动并不影响采用共振反应法来获得模态质量，同时Fz,5的激励方式所得结果欠佳，主要是因为该处的模态向量数值太小所致计算误差较大，故如前面所述激励荷载应选择模态向量数值较大处.

表3 弯桥一阶模态下部分节点振型向量

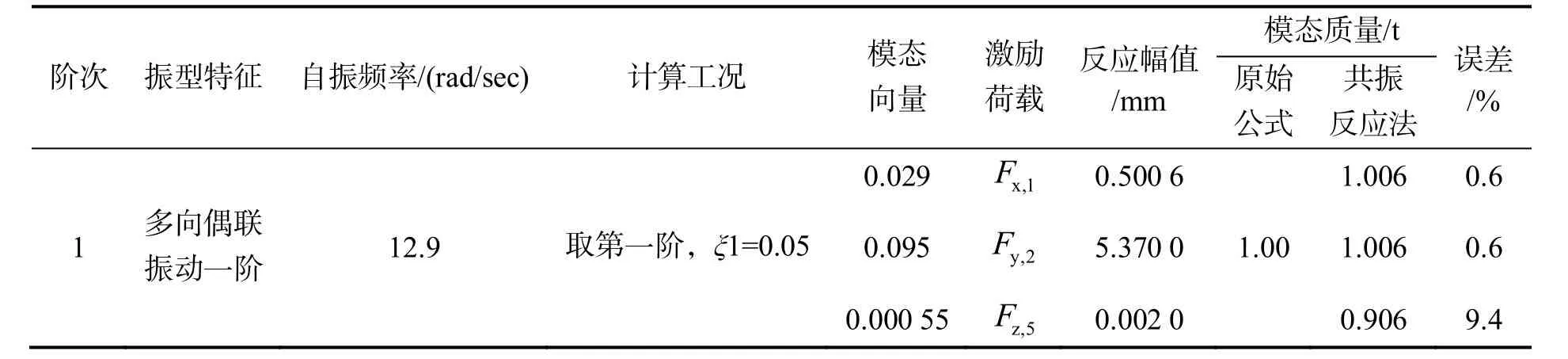
表4 弯桥一阶模态质量计算

5 结语

结构振动系统的模态质量是其控制设计和动力载荷设计的基本参数之一，实际工程结构体系比较复杂，有时结构模型单元数量非常庞大，直接求解模态质量颇为困难，从工程实用角度出发，往往只需获得较低几阶模态质量.

(1)基于单自由度谐振荷载的共振反应，推导得到了一种计算模态质量的新方法；并结合MIDAS有限元分析软件对一简单有限元模型进行模态分析和谐荷载时程分析，得到了模态质量，并通过比较原始定义公式和演化公式计算得到的模态质量，结果表明所提新方法计算结果精度可靠，验证了该方法的可行性及有效性。

(2)模态质量基于模态基向量，算例计算得到的一阶模态质量为1 t，验证MIDAS程序已将模态向量进行模态质量归一处理。

(3)若实际工程中要得到模态最大值归一下的模态质量，则只需将式(16)的最大模态向量φj,n取1即可。

(4)除此，该推导公式同样适用于实验方法获得模态质量。

[1]CHOPRA A K. Dynamics of Structures[M]. New Jersey: Prentice Hall, 1995.

[2]CLOUGH R W, PENZIEN J. Dynamics of Structures[M]. New York: McGraw-Hill Inc, 1993.

[3]陈政清, 华旭刚. 人行桥的振动与动力设计[M]. 北京: 人民交通出版社, 2009.

[4]刘晶波, 杜修力. 结构动力学[M]. 北京: 机械工业出版社,2004.

[5]Penzien W J. 结构动力学[M]. 王光远, 译. 北京: 科学出版社,1981.

[6]孙广华. 曲线桥计算[M]. 北京: 人民交通出版社, 1995.

(责任编校：陈健琼)

A Computing Method Modal Mass Based on the Single Degree of Freedom of Resonance Reaction

HUANG Guoping1,HOU Suwei2,WANG Xinzhong1

（1. School of Civil Engineering, Hunan City University, Yiyang, Hunan 413000, China; 2. School of Civil and Transportation Engineering,Beijing University of Civil Engineering and Architecture, Beijing 102616, China)

Based on the ideas of the resonance response results of the single degree of freedom under harmonic load calculated by the elemental point quality the authors put forward the new way of a multi-degree of freedom structure system to calculate with the modal of the quality. On this method with the finite element software it is to obtain modal quality, to solve a number of problem that the finite element software that it can not extract directly the modal quality. Compared with the results that be calculated by the modal quality in the original formula, the numerical calculation on this method is up to the enough accuracy.

the single degree of freedom; resonance; resonance response; modal mass the finite element software

TU311.3

A

10.3969/j.issn.1672-7304.2017.05.0002

1672–7304(2017)05–0007–05

2017-02-10

国家自然科学基金项目(51508019)；湖南省教育厅科研项目(2017C0304)；2016年益阳市科技计划项目

黄国平(1982-)，男，江西樟树人，讲师，博士研究生，主要从事桥梁结构振动与控制研究. E-mail: 614807827@qq.com