一种OFDM系统稀疏信道估计的有效导频设计方案

翁和王

(武夷学院 数学与计算机学院，福建 武夷山 354300)

一种OFDM系统稀疏信道估计的有效导频设计方案

翁和王

(武夷学院 数学与计算机学院，福建 武夷山 354300)

在正交频分复用(OFDM)系统中，导频信号的选择很大程度上影响了信道估计的性能，研究OFDM系统在稀疏信道的导频配置问题具有重要的意义﹒要找出最佳导频配置，可通过穷尽搜索其所有可能的导频配置，但这会消耗大量的计算时间﹒为了减少计算复杂度，本文引入了交叉熵优化(CEO)算法来确定最优导频配置，同时最大限度地提高稀疏信道估计的精度﹒通过计算机仿真模拟的结果表明，利用该算法获得的导频索引序列比传统平均间隔和随机搜索方法效果更好﹒

信道估计；压缩感应；交叉熵优化；导频位置

信道状态信息(CSI)是提高正交频分复用(OFDM)系统性能的关键因素﹒在实践中，CSI能够根据子载波的使用进行可靠的估计[1]﹒在OFDM系统中，由于导频配置关系到信道估计的质量，所以对OFDM系统中导频的优化进行了大量的研究﹒通过研究发现，在给定数量级的导频信号中，选择等距的音频信号作为导频能够使信道估计的均方差达到最小化﹒

大量的信道测量显示由于散射体的稀疏结构，使得无线信道往往表现稀疏﹒传统的信道估计方案(包括最小二乘法)由于不能利用无线信道固有的稀疏性，对于这样的稀疏通道是无效的[2]﹒此外，应用传统的稀疏信道估计方法也会导致有限资源的过度使用﹒为提高频谱效率，在压缩传感领域中有效的稀疏信道估计算法，如基本追踪(BP)算法和正交匹配追踪(OMP)算法，都可应用到带有少量导频的信道中[3]﹒因此这一工作的重点是压缩传感算法在稀疏信道估计中的应用，该信道导频的数量远小于信道冲击响应信号的数量﹒

然而导频信号的设计直接影响信道估计算法的性能，在进行稀疏信道估计中，传统等距的导频配置对于采用压缩传感算法的稀疏信道估计来说并不是最佳选择﹒对稀疏信道估计的最优导频配置可从对所有可能组合的穷尽搜索中得到，但穷尽搜索所产生的计算复杂度在实际执行时存在潜在的问题﹒为了解决这一问题，很多学者研究稀疏信道估计的最佳导频配置方案[4-6]﹒例如文献[4]提出利用信道数据对导频进行离线训练并完成最优配置方法，但这个方法会占用大量的计算机内存；又如文献[6]提出的交叉熵优化(CEO)算法成功解决了组合优化问题﹒本文利用 CEO算法来搜索最优导频位置，这样可使信道估计的均方差达到最小化﹒

1 系统模型和问题描述

考虑在一个带有N个子载波的 OFDM 系统中选出K个子载波作为接收端已知的导频子载波﹒为便于表示，选定的导频子集位置可表示为

其中n为子载波的下标；pn则表示是否选择n次子载波﹒给定K为已选定子载波p的位置，接收到的导频矢量Y（p）可表示为

由公式(2)得出，信道估计的目标是从Y和A获得hˆ﹒如果矩阵A的列数大于行数（K＞L），那么式(2)中的信道可以通过最小二乘法得到准确的估计﹒然而当导频的数量小于信道系数（K＞L）时，问题就变成不确定了﹒因此，最小二乘法不能提供准确的解决方案﹒考虑到无线信道脉冲响应的固有稀疏性，h的大部分元素都是 0或接近 0，这表明h是一个稀疏矢量﹒在这种情况下，当字典矩阵A满足严格等距属性[7]时，压缩算法提供了一种准确恢复h信号的有效方法﹒通过研究在K＜L稀疏信道估计的情况下，我们可以利用比未知信道系数更少的导频来提高数据率﹒因此，选择恰当的导频至关重要﹒

在给定K导频的情况下出现了以下问题：选择的导频如何影响信道估计误差﹒这个问题直接影响到无线系统的位误码率﹒考虑到典型的信道模型通常是可用的，在传输OFDM信号之前，我们可以使用仿真的信道数据来进行离线导频﹒本文的目标是寻找符合最小均方差的最优化导频配置，具体优化问题可以表示为

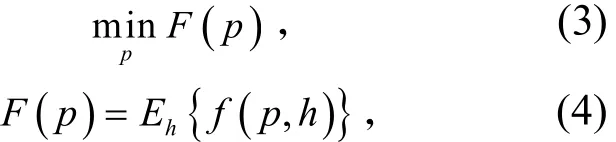
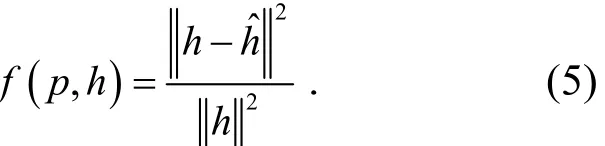
其中式(4)是发射器上可用信道数据的平均均方差；式(5)是特定导频配置p和信道矢量h相对应的表示欧几里得范数；表示通过稀疏信道估计算法获得的信道估计﹒

最直观的方法是给定N和K，最优导频配置p*在上尽可能穷举搜索出符合最小均方差的所有可能导频配置，利用表示二项式系数但上述计算非常复杂，为了减少穷尽搜索的复杂性，本文引进了高效的交叉熵优化(CEO)来确定近乎最优的导频配置﹒

2 交叉熵优化算法设计导频配置

考虑一个最小化问题

其中δ是状态集；G（.）:δ→R是实数函数﹒目标是估计全局最优的解决方案s*∈δ，即标识全局极值在状态集δ上配置﹒为了用交叉熵优化(CEO)解决式(6)，首先必须从特定概率密度函数(PDF)ℓ（·;u）中随机采样候选方案u是控制s中可能解决采样的参数矢量﹒

考虑δ的巨大空间，s*被认为是最优的稀疏方案，交叉熵优化(CEO)把优化问题与稀疏概率估计联系起来﹒最优方案s*认为是稀疏方案，交叉熵优化(CEO)关系到稀疏概率估计优化，我们的问题是估计G(s)小于或等于一个阈值的γ概率可表示为

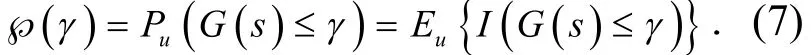
其中uP是范围小于数值γ，接近于γ*的概率；Eu表示相应期望值；s是概率密度产生的随机变量；I（·）是指标函数，当且仅当时，

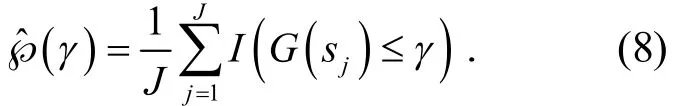
如果公式(10)中的H*当作H，可得到

由于H*涉及未知常量不能直接使用﹒交叉熵优化(CEO)的目的是对带有概率密度函数的H*逼近，它属于的同一家族，但是使用的是不同参数集﹒定位密度尽量减少在和之间的KL(Kullback-Leibler)最小差异(即交叉熵)，可表示为

KL距离定义为

相当于发现

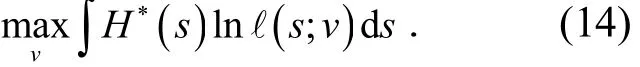
将式(10)代入式(14)，可得

由此等同于

根据样品，可以通过v*得到估计值

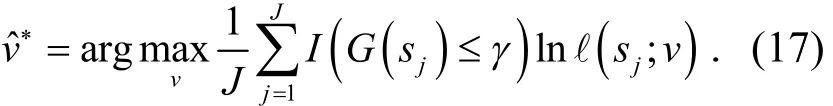
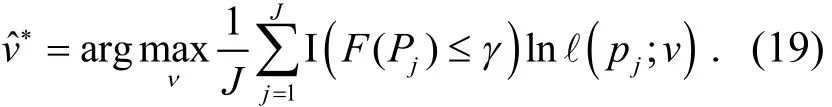
由公式

其中pjn是Pj的第n个元素﹒的重复更新以至于大部分样品产生的满足

3 仿真结果

本文提出交叉熵优化(CEO)用来优化导频配置的方法所使用的参数如下：选定的更新样品部分e=0.1和平滑因子α=0.8，为了减少CEO的复杂度，可以在迭代次数t达到最大的情况下终止该算法﹒假设本文预定义的迭代次数t=50，通过对目标函数的大量评估来分析CEO计算复杂度，CEO计算复杂度近似为小于穷尽搜索复杂度﹒在 OFDM 信号传送之前给定离线导频设计，CEO的计算复杂度仍然是可接受的﹒

在训练信道中，不同的J值所设计的MSE性能，利用LASSO算法[9-10]中的压缩传感算法来计算导频数据的稀疏信道估计，如图1所示﹒可见穷尽搜索算法只能通过所有可能导频位置的有限子集进行比较和评估﹒

图1 不同J值的基于CEO优化的导频位置收敛

在研究中，随机生成和评估了5 000，10 000，15 000和20 000共4个不同的导频位置﹒图1显示MSE的性能随着CEO迭代次数的增加有着明显的改善，当迭代次数达到大约 41，MSE值在J=150时达到最优值，并且 CEO会将收敛得到的最好结果与其他不同的J值相比较，从而得到一个合理的解决方案﹒因此，我们选择J=150进行仿真，同时，在MSE的基础上利用CEO算法获得的优化导频特性明显优于使用有限子集的穷尽搜索算法，这也说明CEO算法作为OFDM导频优化设计工具在稀疏信道估计场景是有效的﹒

在不同信噪比率(SNR)中，均分布的导频配置、随机导频配置和基于CEO的优化导频配置3种情况下的MSE性能关系见图2﹒由图2可知在整个信噪比中，该导频序列的MSE性能明显优于随机导频序列和平均间隔导频的性能﹒为了验证本文算法的健壮性，考虑的OFDM 系统，对具有大量子载波信道数目的OFDM系统进行测试见图3﹒图3显示了不同方案下对应SNR的信道估计比率MSE性能，由此可见本文提供的算法远优于其他算法，说明了本文算法的健壮性和有效性﹒

图2 不同导频分配方案MSEamp;SNR ((N,K)=(256,16))

图3 不同导频分配方案MSEamp;SNR ((N,K)=(512,16))

4 结论

研究影响信道估计性能的导频配置是重要且困难的组合优化问题，本文提出的交叉熵优化(CEO)算法在稀疏信道估计场景中优于OFDM导频模式﹒仿真结果表明，相比均分布导频和随机导频，本文提出的基于导频配置的估计信道对MSE性能有着较大幅度的提高﹒

[1]NEGI R, CIOFFI J. Pilot tone selection for channel estimation in a mobile OFDM system[J]. Consumer Electronics IEEE Transactions on, 1998, 44(3): 1122-1128.

[2]CARBONELLI C, VEDANTAM S, MITRA U. Sparse channel estimation with zero tap detection[J]. Wireless Communications IEEE Transactions on, 2007, 6(5): 1743-1763.

[3]BERGER C R, WANG Z, HUANG J, et al. Application of compressive sensing to sparse channel estimation[J].Communications Magazine IEEE, 2010, 48(11): 164-174.

[4]QI C, WU L. Optimized pilot placement for sparse channel estimation in OFDM systems[J]. IEEE Signal Processing Letters,2011, 18(12): 749-752.

[5]QI C, WU L. A study of deterministic pilot allocation for sparse channel estimation in OFDM systems[J]. IEEE Communications Letters, 2012, 16(5): 742-744.

[6]RUBINSTEIN R Y, KROESE D P. The cross-entropy method[J].Technometrics, 2008, 50(1): 92-92.

[7]CANDES E J, TAO T. Near-optimal signal recovery from random projections: universal encoding strategies?[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425.

[8]Recommendation ITU-R M.1225, Guidelines for evaluation of radio transmission technologies for IMT-2000[S]. 1997.

[9]BERG E V D, FRIEDLANDER M P. Sparse optimization with least-squares constraints[J]. SIAM Journal on Optimization, 2011,21(4): 1201-1229.

[10]TIBSHIRANI R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society, Series B(Methodological), 1996, 58(1): 267–288.

(责任编校：龚伦峰)

An Efficient Pilot Design of Sparse Channel Estimation for OFDM System

WENG Hewang
(School of Mathematics and Computer, Wuyi University, Wuyishan, Fujian 354300, China)

In the orthogonal frequency division multiplexing (OFDM) system, the selection of pilot signal is of great influence on the performance of channel estimation of OFDM system in the pilot allocation problem of sparse channel. In order to find the optimal pilot configuration, searching all the possible pilot allocation through exhaustive effort, it will consume a large amount of computing time. In order to reduce the computational complexity, this paper introduces the cross entropy optimization (CEO) algorithm to determine the optimal pilot configuration, while maximizing the sparse channel estimation accuracy. Through the computer simulation results show that using pilot sequence index obtained by this algorithm than the traditional average interval and random search method is better.

channel estimation; compressed sensing; cross entropy optimization; pilot placement

TN919.3

A

10.3969/j.issn.1672-7304.2017.05.0012

1672–7304(2017)05–0056–05

2017-07-16

福建省教育厅科研项目(JA15527)

翁和王(1983- )，男，福建南平人，讲师，硕士，主要从事智能图像技术研究﹒E-mail: 913954309@qq.com