半线性椭圆型方程多解计算的Newton流线法

李夏云，熊佩英，陈传淼

(1. 湖南城市学院 理学院，湖南 益阳 413000；2. 湖南师范大学 数学与计算机科学学院，长沙 410081)

半线性椭圆型方程多解计算的Newton流线法

李夏云1，熊佩英1，陈传淼2

(1. 湖南城市学院 理学院，湖南 益阳 413000；2. 湖南师范大学 数学与计算机科学学院，长沙 410081)

为求解半线性椭圆方程的多解问题，本文在搜索延拓法理论的基础上，改用Newton流方程来计算目标方程组，进而提出了新的Newton流线法，证明了其具有指数收敛性，并给出了其算法；如果大量随机地投入初始点，通过该方法能得到半线性椭圆方程的所有解；最后其有效性为正方形域中立方非线性方程的多解数值实验所证明﹒

非线性；多解；Newton流线法；中心场

半线性椭圆型方程问题

式(1)中Ω是RN上的有界区域，假设非线性项f(x,u)在Ω×R上满足局部 Lipschitz连续，且其中a1,a2为正常数，当当时，方程(1)的能量泛函为

对于方程(1)的解的存在性与多解性，已经有大量的研究成果，其多解的数值计算也有大批的研究者进行了关注[1-7]﹒在方程(1)中取则有

此算法的第1步搜索所有的解的初值是决定性的，在多解计算中，遇到的困扰是发散﹒由于初值的原因，加上E(u)常是非凸的，对于高Morse指标，使得迭代计算很不稳定，因此我们提出Newton流线法来大范围求解半线性椭圆方程的多解问题﹒Newton流线法：大量随机地投入初始点，使解曲线沿着 Newton流方向，可大范围按指数收敛，自适应地追踪根，从而求得半线性椭圆方程的所有解﹒

1 半线性椭圆方程的多解计算分析

1.1 Newton流线法的基本理论

设n阶非线性方程组为

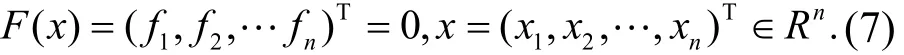
其中F(x)是从N维区域的连续且分片光滑的函数，其经典的求解方法是 Newton迭代法[7]：其有二阶收敛性，其需要很好的初值x0，仅当初值很接近真解x*时才是收敛的﹒理想的算法是：计算轨道总是沿着的方向前进，在 Davidenko方程中，令t=0，可得它与流线的方向是一致的，当t＞0时，因初值x0的影响，曲线x(t)逐渐偏离了流线方向V(x)﹒为此我们考虑Newton流方程，即

对于任意的初值x0，式(8)准确地描述了流线的微分方程，始终沿着流线方向前进﹒求解式(8)，我们采用的具有k≥1阶精度的Euler格式为

当k=1时，有在计算接近根的时，F(x)变小，流线方向V(x)也变得很小，x(t)的变化很小，当t→∞时，才有x(t)→x*，t适当大以后，可改用较大的步长来计算；当计算的根达到一定的精度以后，即可以终止计算，也可改用牛顿迭代求解，直到得到所需的根x*﹒

在企业集团战略性成本管理中，为了将成本管理工作作为重点,结合成本工作的特点，进行管理方案的创设，优化成本控制的内容，为成本管理工作的完善提供支持。在成本管理控制体系确定中，应该结合成本管理的特点，进行各个部门之间的工作协调，使企业各项经营活动得到整合，优化成本管理流程，为财务工作的创新提供支持，降低企业成本支出，为企业运营成本以及定量工作的分析提供参考，促进企业的经济发展[4]。

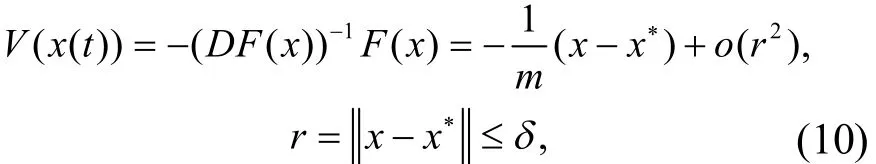
即其形成一个向x*汇聚的Newton中心场﹒

证明：以x*为球心建立坐标系，设B(θ)为单位球，则一个朝x*汇聚的中心场为

在x*的邻域中，有

设x*=0，展开为x的m次齐次多项式，对任意的参数μ恒有关于μ求导得

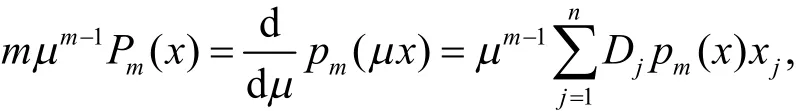
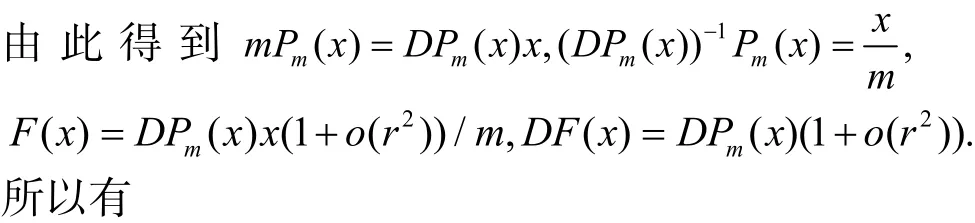
定理 2：设F(x)为闭子域G∈Ω上的适当光滑的函数，x*是F(x)的m重根，则以任意x0∈G为起点的用k≥1阶数值方法确定的场线x(t)，满足，且适当多步以后x(t)按指数衰减估计，

由定理1展开

1.2 求所有根的Newton流线算法

为求非线性问题的根，基于上面理论，我们提出Newton流线算法：设有界区域G将被F的奇异面分为若干个联通的子域Gj，其中一些子域含有一个根，任取其中一点为起始点，用Newton流线法可以求得此根；有些子域没有根，任取其中一点为起始点得到的点列将接近某奇点，终止计算﹒

第1步：随机取初始点x0，计算

第3步：判断x0和xk是否是根或者是奇异点若其不是，继续用流线法计算，适当多步以后，若满足则可得到一个近似的根，若不是重根，以后改用牛顿迭代法加速；若仍有则此子域无根，停止迭代并转向另一初值点，再进行第2步计算﹒

第4步：将所求根存在数组U中(计算的第一个根必存)，以后每得到一个根与先存的比较，若则xi*是新根，可存入U，否则弃去并终止计算，最后将在U中存下所有不同的根﹒

2 正方形域上半线性椭圆方程的多解计算研究

3 正方形域上半线性椭圆方程多解的Newton流线计算法

首先用不同类型基函数组合来求问题的解﹒按特征值的大小取

这7个值中，有2个二重值，3个单值，按前面的搜索延拓法应该可以得到 22个非零解﹒其近似解u7(x,y)的系数满足非线性方程组

我们用 Newton流线法来对其进行计算：在区域[-3,3]上随机取点，并取 30000n= ，再调用Matlab中的 rand函数，得到一个7×30 000的随机矩阵，共30 000个初值，通过计算，得到50个非零解，与前面的22个解比较，多了28个不同的解，将其进行归类，得到15组解﹒利用区域的对称性归类，我们得到3组不同的新解，这3组不同的新解是不同的特征值与对应的特征函数的相互作用，而产生的多解﹒设这 3组新解为它们对应的初值分别为

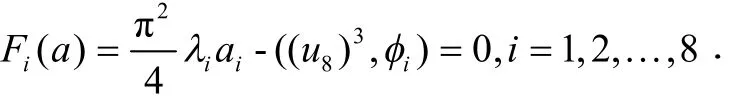
利用Newton流线法来计算，共得到84个非零解，利用区域的对称性，通过归类，我们得到26组不同的解﹒不同的特征值之间可以产生新的多解﹒

4 总结

求解半线性椭圆方程的多解问题，先用随机函数，将基进行线性组合，随机布点，然后用Newton流线法来搜索更好的初值，最后在最大的子空间用 Newton法或其他迭代法求解目标方程组，最后可得到所求问题的真解，且真解与初值的图像很相似，只是真解的腰更细、峰更高，这说明了本文方法是可行的﹒

图1 初值u1图像

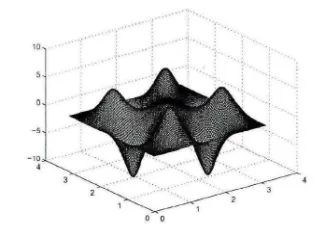
图2 真解u1图像

图3 初值u2图像

图4 真解u2图像

图5 初值u3图像

图6 真值u3图像

实验中从 500～30 000每隔 500个点，用Newton流线法求解，最初采用随机函数进行随机取点，求解结果如图7所示﹒

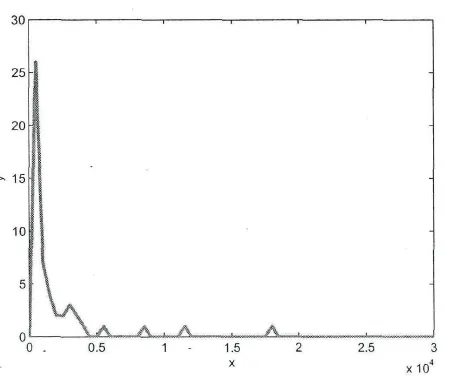
图7 每隔500个点记录的解个数图

图7中记录了数值实例在区域[-3,3]上搜索到的解的情况，可以看出Newton流线法求解半线性椭圆方程的多解，可以搜索出全部解的概率大约是99.9%，但此类多解计算问题计算量很大﹒上例中取8个基，随机投入35 000个初始点，每个点迭代20次，对于系数方程式(11)要计算74.48× 10个积分﹒由于基的选取，迭代的步数，取点的个数不同而导致计算量大小各异，基取得越多计算量越大，此算法若采用并行计算可一定程度上提高解题的效率﹒

[1]CHOI Y S, MCKENNA P J. A mountain pass method for the numerical solutions of semilinear elliptic problems[J]. Nonlinear Analysis: Theory, Methods amp; Applications, 1993, 20(4): 417-437.

[2]DING Z H, COSTA D, CHEN G O. A high-linking algorithm for sign-changing solutions of semilinear elliptic equations[J].Nonlinear Analysis, 1999, 38(2): 151-172.

[3]LI Y X, ZHOU J X. A minimax method for finding multiple critical points and its applications to semilinear PDEs[J]. Siam Journal on Scientific Computing, 2001, 23(3): 840-865.

[4]陈传淼, 谢资清. 非线性微分方程多解计算的搜索延拓法[M].北京: 科学出版社, 2005.

[5]陈传淼. 科学计算概论[M]. 北京: 科学出版社, 2007.

[6]WANG Z Q. On a superlinear elliptic equation[J]. Annales De L Institut Henri Poincare Non Linear Analysis, 1991, 8(1): 43-57.

[7]李庆扬, 莫孜中, 祁力群. 非线性方程组的数值解法[M]. 北京: 科学出版社, 1999.

(责任编校：龚伦峰)

Newton Flow Method for Solving Multiple Solutions of Semi-Linear Elliptic Equations

LI Xiayun1, XIONG Peiying1, CHEN Chuanmiao2
(1. College of Science, Hunan City University, Yiyang, Hunan 413000, China; 2. College of Mathematics and Computer Science, Hunan Normal University, Changsha, Hunan 410081, China)

To solve the multiple problem of the semi-linear elliptic equation, on the basis of searching the theory of extension method, the Newton flow equation is used to calculate the target system, and then the new Newton flow-line method is proposed, the exponential convergence is proved, and its algorithm is given, if it puts into a large number of the stochastic initial point, which can obtain all solutions of the semi-linear elliptic equation. Finally, its efficiency is proved by the multiple value experiment of cubic nonlinear equation in square domain.

nonlinear; multiple solutions; Newton flow-line method; central field

O241.7；O241.81

A

10.3969/j.issn.1672-7304.2017.05.0010

1672–7304(2017)05–0046–05

2017-08-09

湖南省教育厅科研项目(15C0243)

李夏云(1972- )，女，湖南益阳人，副教授，硕士，主要从事数值计算研究﹒E-mail: 1270003202@qq.com