全光纤干涉式结构中传感模式仿真分析∗
2017-12-05李丽君马茜曹茂永宫顺顺李文宪丁小哲郭晓丽刘仪琳徐琳刘倩
李丽君马茜曹茂永 宫顺顺 李文宪 丁小哲 郭晓丽 刘仪琳 徐琳 刘倩
1)(山东科技大学,电子通信与物理学院,青岛 266590)2)(山东科技大学,电气与自动化工程学院,青岛 266590)3)(山东科技大学,矿山灾害预防控制省部共建国家重点实验室培育基地,青岛 266590)
全光纤干涉式结构中传感模式仿真分析∗
李丽君1)2)3)马茜2)曹茂永2)3)†宫顺顺1)李文宪1)丁小哲1)郭晓丽1)刘仪琳1)徐琳1)刘倩1)
1)(山东科技大学,电子通信与物理学院,青岛 266590)2)(山东科技大学,电气与自动化工程学院,青岛 266590)3)(山东科技大学,矿山灾害预防控制省部共建国家重点实验室培育基地,青岛 266590)
(2017年5月10日收到;2017年8月4日收到修改稿)
全光纤干涉式传感结构中包层模场与外界物理量作用,携带被感测信息,因此对包层模的研究是设计制作和提高该类传感器传感性能的关键.利用有限差分光束传播法获得传感光纤不同长度和不同芯径比时传感器对应的光谱,通过傅里叶变换获得其干涉频谱,计算出各主要参与干涉的包层模组的有效折射率,利用色散方程确定对应包层模.理论仿真结果显示,随着传感部分光纤长度增加,参与干涉的包层模式随之增加,并且向高阶模式变化,光谱变得稠密,是多阶包层模干涉的叠加,传感器输出干涉谱的自由光谱范围变小.随着输入光纤与传感光纤芯径比变化,会明显改变纤芯包层功率分布,同时,芯径比增大也会增加参与干涉的包层模种类和阶数.
全光纤干涉仪,有效折射率,包层模,频谱
1 引 言
全光纤干涉式传感结构主要包括全光纤Mach-Zehnder(M-Z)干涉仪及Michelson干涉仪结构,由于其具有结构简单、灵敏度高和制作成本低等特点,在折射率、应力、温度和气体浓度检测等方面的应用体现出独特的优势[1−4].该类传感器一般采用纤芯失配型光纤结构,即通过不同尺寸纤芯光纤间的熔接带来的半径不匹配来激发传感部分光纤的包层模,再将包层模耦合回纤芯并与纤芯模干涉,形成基于干涉原理的全光纤干涉式传感结构.该结构中包层模场与外界物理量作用,携带被感测信息,因此确定和控制包层模是设计和制作该类传感器的关键.
1997年,Channing等[5]首次提出纤芯失配型光纤传感结构,并论述了该结构在有效折射率检测方面的独特优势.对于该类传感器的包层模式的研究开始于2007年,Choi等[6]提出了一种单模-光子晶体-单模光纤结构,通过理论和实验对比传感器输出干涉谱,得出了传感光纤长度和不同的熔接方法是改变包层模的关键的结论.2008年,Hguyen等[7]对多模-单模-多模光纤结构中不同长度单模光纤中的包层模式进行了分析,得到光纤长度越长参与干涉的包层模阶数越高的结论.之后,对于该类传感结构中包层模的分析主要为针对各不同的纤芯失配型结构相对应的干涉谱、通过傅里叶变换来分析包层模与传感部分光纤长度关系.如,2012年,Li等[8]对基于M-Z干涉的多模-小芯径-单模的纤芯失配型结构中的小芯径光纤长度与激发包层模情况进行了分析.同年,Rong等[9]对基于M-Z干涉的小芯径-单模-小芯径纤芯失配型结构的模式与长度的关系进行了分析.2013,该团队又对基于Michelson干涉的单模-多模-单模纤芯失配型结构进行了多模光纤的耦合模式与长度关系分析[10].2015年,Fu等[11]提出了一种小芯径-多模-小芯径的纤芯失配型光纤结构,并对中间段的多模光纤进行了耦合模式的分析等.可见,已有的报道为该类传感结构中包层模的分析提供了理论依据和方法,对传感器制作和传感性能的分析具有指导意义.然而,目前还存在两个亟待解决的问题,首先需要一种确定包层模式的方法,包层模式确定对于传感器传感特性研究非常关键;其次是除了光纤长度以外,还有哪些主要因素是决定哪些包层模参与传感的关键,这种因素与参与干涉的包层模间的关系.
本文通过beam prop软件利用有限差分光束传播法对不同长度光纤和不同芯径比的纤芯失配型光纤结构进行了光谱仿真,通过光谱傅里叶变换的方法,获得了不同传感结构输出光谱的空间频率,用来获得主要参与干涉的包层模式.通过包层模有效折射率与传感部分光纤的各阶包层模色散关系曲线对比,最终确定主要包层模阶数范围.传感光纤前面多采用多模光纤,用以造成纤芯失配结构,不同的多模光纤与传感光纤的芯径比,是决定输入功率耦合入纤芯模和包层模光功率的关键,这个功率耦合比也直接影响着该传感结构中参与干涉的包层模种类和数量,通过理论模拟不同芯径比纤芯失配型传感结构空间频率,可见芯径比越大,包含的包层模种类越多.
2 理论分析
纤芯失配型光纤结构如图1所示,是由芯径不同的光纤或错位或同轴熔接在一起制作而成.光从输入光纤进入传感光纤,再经输出光纤,最后耦合到输出单模光纤,输入光纤芯径一般大于传感光纤,在它们的熔接点1处,光被分成两束,一束进入传感光纤纤芯,另一束进入传感光纤包层,激发起高阶包层模,由包层模场与外界作用,携带外界信息,实现传感.在传感光纤与输出光纤熔接点2处,包层模被耦合进光纤纤芯,继续耦合入输出单模光纤纤芯,由于纤芯模式与包层模式经历的光程不同,因而在输出光纤中形成干涉谱,通过测量该干涉谱即可获得传感信息.
图1结构可以看作全光纤M-Z干涉仪,其输出的干涉光强为[12]

其中,Icore,Icladding分别代表光纤纤芯模的光强和包层模的光强,ϕ为纤芯模和包层模的相位差,可表示为

其中,k为波数,L为传感光纤长度,∆neff为纤芯与第m阶包层模的有效折射率差,表示为
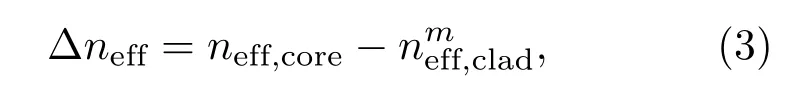
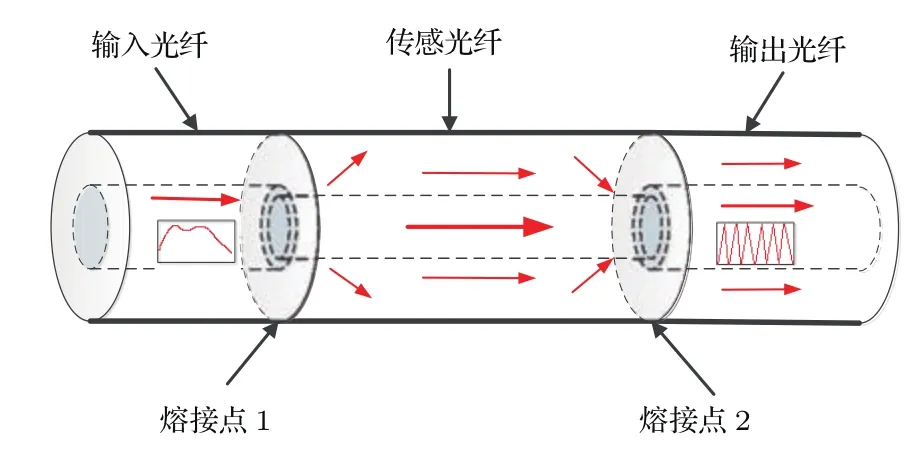
图1 (网刊彩色)纤芯失配型光纤结构Fig.1.(color online)Core mismatch optical fiber sensing structure.
由于不同的包层模对应不同的波数,将相位差以中心波长λ0泰勒展开,取第一项可表示为

其中,ϕ0为泰勒展开第一项,∆λ为模式间的波长差.
由于包层模式数量巨大,即使对应同一阶高阶包层模也存在数量巨大的简并模式,因此在分析过程中,只能确定出有效折射率相近的主要参与干涉的包层模组.因此,用包层模组的有效折射率差∆meff代替(4)式中的∆neff,它们之间的关系式为

根据傅里叶变换后光谱的相位差与空间频率关系为

其中,ζ为空间频率.
由于光纤较短材料色散可以忽略,综合(4)—(6)式,可得
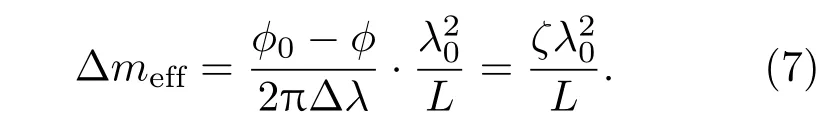
因此,通过傅里叶变换后的空间频率即可获得包层模组的折射率范围.此外,将光纤假设为三层结构,运用区间遍历及裁弦法对纤芯失配型的中间段光纤进行包层模有效折射率求解[13],即可确定包层模组对应的包层模阶数,从而找出参与干涉的包层模种类.
3 仿真与分析
以图1结构为例,运用beam prop仿真,其光强分布情况如图2所示,其中,传感光纤纤芯包层直径参数为4.2/125µm,长度为3 cm,输入和输出光纤均为8.2/125µm,中心波长为1550 nm.
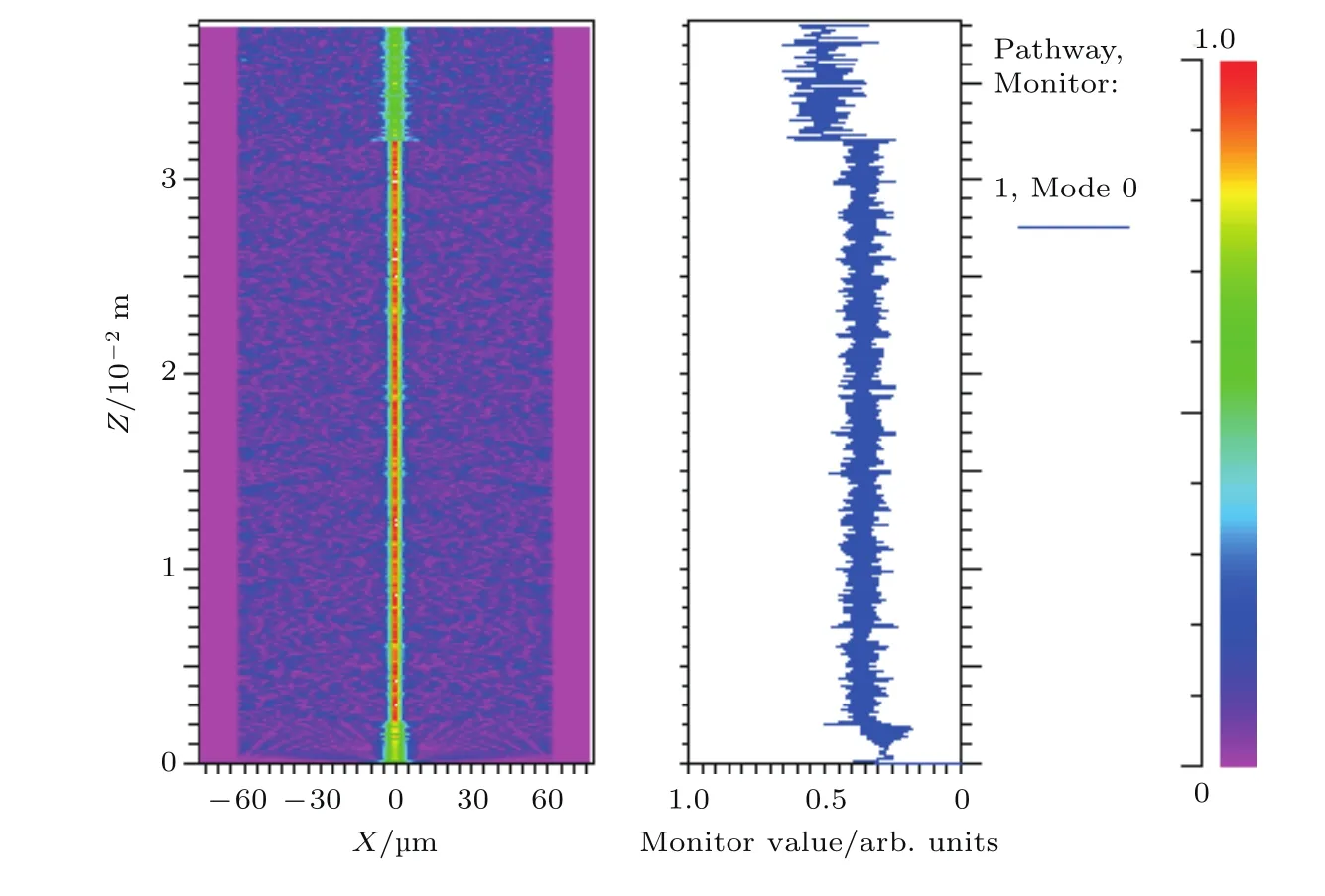
图2 (网刊彩色)全光纤干涉式光纤结构光强分布情况Fig.2.(color online)Intensity distribution of in- fiber interferometer.
从光强分布图可以清楚看出,在传感光纤中,大部分能量集中在光纤芯中,一部分光能进入到包层中,并激起了大量包层模存在于传感光纤的包层中,输出光纤纤芯中形成了清晰的干涉现象.将波长为1530—1570 nm范围内的宽带光输入以上传感结构,利用有限差分光束传播法,该波段内对应不同传感部分光纤长度的输出光谱模拟图如图3所示.
图3中可见清晰的干涉现象,干涉谱不是很均匀,这是由于参与干涉的包层模比较多,清晰的干涉谱主要来源于高阶包层模与纤芯模的干涉,即由不同空间频率的多个干涉谱叠加而成,低阶包层模与纤芯模干涉形成的自由光谱范围比较大,高阶包层模与纤芯模干涉谱的自由光谱范围比较小,该现象从图3(a)—(d)的对比可清楚地看出,干涉谱随着光纤长度的增加在相同波长范围内,光谱变得越来越稠密,自由光谱范围越来越小,每个干涉谱边缘变得尖锐.由图3(c)和图3(d)可见,除了稠密的干涉谱本身,整体光谱还存在包络光谱,该包络干涉是由低阶包层模干涉形成的.由此可见,全光纤干涉式结构的干涉过程复杂,想要获得具体空间频率成分,需要对输出光谱进行傅里叶变换,分析其频率成分,从而得到干涉谱中参与干涉的主要包层模成分,并确定耦合模式的种类,经傅里叶变换后的不同长度光纤对应的空间频率图如图4所示.
从图4(a)—(d)中均可以看出,在空间频率为0附近幅值最大,为光的能量主要集中区域,为LP01纤芯模,是主要参与干涉的模式.图4(a)对应传感部分光纤为1 cm时,在靠近纤芯模附近存在一包层模组,对应空间频率ζ=0.0245,运用(7)式可以求出其有效折射率的差,进而求取包层有效折射率,有效折射率与色散方程对应,即可确定该包层模组的模阶数,经计算该模式组为第6阶包层模及其简并模式.图4(b)对应光纤长度为3 cm,空间频率图较4(a)变大,计算得到该干涉模组为第8阶包层模及其简并模式.图4(c)对应光纤长度为5 cm,出现了两组主要参与干涉的包层模组,经计算得到其分别对应于第6和第8阶包层模及其简并模式.图4(d)对应光纤为7 cm,出现了更多的包层模群,经计算分别对应6阶、8阶和12阶等包层模组.
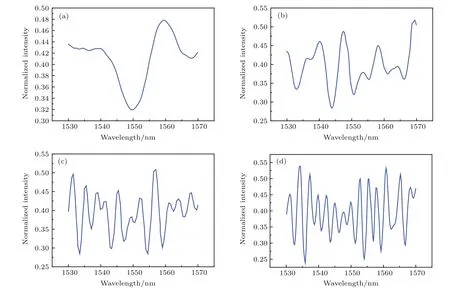
图3 长度分别为(a)1 cm,(b)3 cm,(c)5 cm和(d)7 cm的干涉仪输出光谱仿真Fig.3.Simulation results of transmission interference spectrum of sensing part optical fiber length as(a)1 cm,(b)3 cm,(c)5 cm and(d)7 cm,respectively.

图4 不同传感长度(a)1 cm,(b)3 cm,(c)5 cm,(d)7 cm光谱傅里叶变换图Fig.4.Fourier transformed spetrum of sensing fiber length as(a)1 cm,(b)3 cm,(c)5 cm and(d)7 cm,respectively.
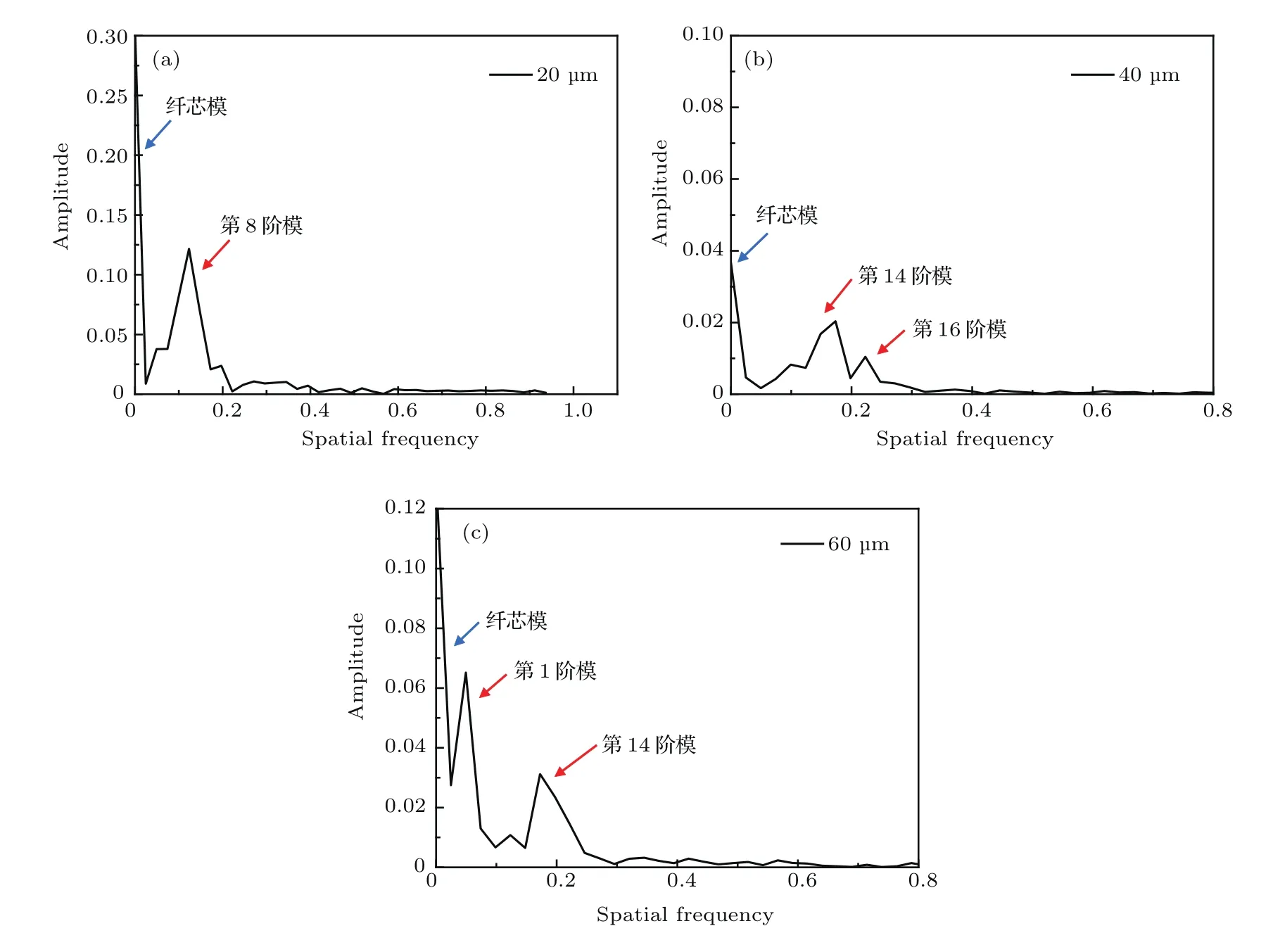
图5 不同多模光纤直径(a)20µm,(b)40µm,(c)60µm对应的空间频谱图Fig.5.Fourier transformed spetrum of interferometers when the fiber diameter as(a)20 µm,(b)40 µm and(d)60µm,respectively.
从以上分析可见,随着传感光纤长度的变化,参与干涉的包层模阶数逐渐变大,对应的空间频率增大.对该类光纤传感器干涉谱影响比较大的因素还包括输入光纤与传感光纤的芯径比,1997年,Channing等[5]就从纤芯/包层功率耦合比入手对比进行了简单的理论论述.但是,通常该功率的测量是比较困难的,因此本文从输入光纤与传感光纤在第一个熔接点处的芯径比入手来讨论参与干涉的包层模情况.图5为不同芯径比情况下的对应频谱图.
图5为输入多模光纤直径分别20µm,40µm和60µm和传感光纤模场直径为5µm时,即芯径比分别为4,8,12的输出干涉光场频谱图,从图中可以看出,当芯径比不同时,纤芯模(空间频率0点)和包层模的比例发生了明显变化,芯径比越大参与干涉的包层模组数越多,而且激发的模组阶数不容易确定,但总体空间频率增大.通过上面的分析可知这意味着参与干涉包层模阶数变大,也就是更多的包层模参与干涉.因此,芯径比的改变从根本上影响了参与耦合的包层模的种类和阶数,且当芯径比越大时,激发出新的包层模也越多.
在实际应用中,并不能根据需要随意改变光纤的半径,为此很多光纤传感器采用了错位熔接的方式进行熔接,力求激发更多的包层模与外界产生能量交换,从而提高光纤传感器的灵敏度.
4 结 论
本文讨论了一种全光纤干涉式传感结构中的干涉谱中包层模阶数确定的方法,并仿真分析了光纤长度及芯径比与该类传感结构中主要干涉包层模间的关系.结果显示,传感光纤长度的增加会使传感器干涉谱变得稠密,高阶包层模干涉具有较小的自由光谱范围,会使参与干涉的包层模阶数增大,参与干涉的包层模式种类增加.通过空间光谱得到主要参与干涉包层模组的有效折射率,代入传感光纤色散方程即可得出对应包层模的阶数,从而确定包层模种类.在传感光纤长度不变的条件下,研究了芯径比对包层模的影响,结果表明随着芯径比的变大,激发的包层模种类也会变多,从而增大了与外界环境的能量交换,进一步提升了灵敏度.由于高阶包层模模场直径比较大,当利用包层模来携带被测信息时,其与光纤包层外被测物理量能够进行更有效的接触.因此,较高阶的包层模与纤芯模干涉会具有较高的传感灵敏度.从理论模拟可见,增加传感部分光纤长度和改变输入光纤与传感光纤芯径比,均可以激发更多的高阶包层模参与传感光谱中.然而,太密集的光谱对于解调设备的分辨率也会带来较高的要求及增大传感器尺寸;同时,大的芯径比又为传感器带来较大的光功率损耗,因此在设计和制作传感器时,需要综合考虑以上因素.本文理论及仿真研究结果可为该类光纤传感器的设计和传感性能的研究提供帮助.
[1]Li L J,Ma Q,Cao M Y,Zhang G N,Zhang Y,Jiang L,Gao C T,Yao J,Gong S S,Li W X 2017Sens.Mater.29 15
[2]Rong Q Z,Qiao X G,Du Y Y,Sun H,Feng D Y,Wang R H,Hu M L,Feng Z Y 2013Applied Opt.52 1441
[3]Zhu J J,Zhang P A,Xia T H,et al.2010IEEE Sens.J.10 1415
[4]Li L J,Ma Q,Zhang Y,Cao M Y,Zhang G N,Jiang L,Gao C T,Yao J,Li Y D,Gong S S,Li W X 2017Sens.Actuat.B234 674
[5]Canning J,Garter A L 1997Opt.Lett.22 561
[6]Hae Y C,Myong J K,Byeong H L 2007Opt.Express15 5711
[7]Linh V N,Dusun H,Sucbei M,Dae S M,Youngjoo C 2008Opt.Express16 11369
[8]Li L C,Xia L,Xie Z H,Liu D M 2012Opt.Express20 11109
[9]Rong Q Z,Qiao X G,Du Y Y,Feng D Y,Wang R H,Ma Y,Sun H,Hu M L,Feng Z Y 2012IEEE Sens.J.12 2501
[10]Rong Q Z,Qiao X G,Du Y Y,Feng D Y,Wang R H,Ma Y,Sun H,Hu M L,Feng Z Y 2013Appl.Opt.52 1441
[11]Fu H W,Li H D,Shao M,Zhao N,Liu Y G,Li Y,Yan X,Liu Q P 2015Opt.Lasers Eng.69 58
[12]Li L C,Xia L,Xie Z H,Hao L N,Shuai B B,Liu D M 2012Sens.Actuators A:Phys.180 19
[13]Li L J,Lai Y Z,Cao M Y,Liu C,Yuan X M,Zhang X,Guan J P,Shi J,Li J 2013Acta Phys.62 140201(in Chinese)[李丽君,来永政,曹茂永,刘超,袁雪梅,张旭,管金鹏,史静,李晶2013物理学报62 140201]
PACS:02.30.Gp,02.60.Cb,42.81.–i,81.05.–tDOI:10.7498/aps.66.220202
*Project supported by the Shandong Provincial Natural Science Foundation of China(Grant Nos. ZR2009AM017,No.ZR2013FM019),the National Postdoctoral Project of China(Grant Nos.200902574,20080441150),Shandong Provincial Education Department Foundation of China(Grant No.J06P14),Qingdao Development Zone Project,China(Grant No.02030093101)and Opening Foundation of State Key Laboratory of Minning Disaster Prevention and Control Co-founded by Shandong Province and the Ministry of Science and Technology,China(Grant No.MDPC201602).
†Corresponding author.E-mail:nankaillj@163.com
Simulation and analysis of sensing modes of in- fiber interferomete∗
Li Li-Jun1)2)3)Ma Qian2)Cao Mao-Yong2)3)†Gong Shun-Shun1)Li Wen-Xian1)Ding Xiao-Zhe1)Guo Xiao-Li1)Liu Yi-Lin1)Xu Lin1)Liu Qian1)
1)(College of Electronics,Communication and Physics,Shandong University of Science and Technology,Qingdao 266590,China)2)(College of Electrical Engineering and Automation,Shandong University of Science and Technology,Qingdao 266590,China)3)(State Key Laboratory of Mining Disaster Prevention and Control Co-founded by Shandong Province and the Ministry of Science and Technology,Shandong University of Science and Technology,Qingdao 266590,China)
10 May 2017;revised manuscript
4 August 2017)
The cladding mode of the in- fiber interference sensor relates to the externally sensing physical quantity,so the investigation of the cladding mode is very important for designing and improving the sensing performance of the sensor.By using the finite di ff erence beam propagation method,the interference spectra of the sensors with di ff erent lengths and di ff erent core-to-core diameter ratios are simulated.Its spatial frequency spectrum is obtained through Fourier transform.The e ff ective refractive index of the dominant cladding mode can be obtained through analyzing its spatial frequency spectrum.Its corresponding cladding mode order can be determined through substituting the values of the e ff ective refractive index into the dispersion equation of sensing optical fiber.The simulation results show that the number and the order of the cladding modes both increase with sensing part fiber length increasing.The interference spectrum becomes dense according to the superposition of multi order cladding mode interferences.Its free spectral space of the sensor output interference spectrum becomes small.With the variations of the input fiber and sensing fiber core-to-core diameter ratio,the power distributions among the modes change obviously.The increase of core-to-core diameter ratio can increase the number and order of the cladding modes.
all in- fiber interferometer,e ff ective refractive index,cladding modes,spatial frequency spectrum
10.7498/aps.66.220202
∗中国博士后特别资助项目(批准号:200902574)、中国博士后面上资助项目(批准号:20080441150)、山东省自然基金(批准号:ZR2009AM017,ZR2013FM019)、山东省教育厅(批准号:J06P14)、青岛开发区(批准号:2007-2-39)和矿山灾害预防控制省部共建国家重点实验室培育基地开放基金(批准号:MDPC201602)资助的课题.
†通信作者.E-mail:nankaillj@163.com
