漂浮式独塔斜拉桥竖弯刚度评估新方法

康厚军，苏潇阳，龚平，蔡向阳，刘海波，胡建华，郭铁丁

(1.湖南大学 土木工程学院，湖南 长沙 410082； 2.湖南省汝郴高速公路建设开发有限公司，湖南 郴州 423000；3.湖南省交通规划勘察设计院，湖南 长沙 410008)

漂浮式独塔斜拉桥竖弯刚度评估新方法

康厚军1†，苏潇阳1，龚平2，蔡向阳2，刘海波3，胡建华3，郭铁丁1

(1.湖南大学 土木工程学院，湖南 长沙 410082； 2.湖南省汝郴高速公路建设开发有限公司，湖南 郴州 423000；3.湖南省交通规划勘察设计院，湖南 长沙 410008)

斜拉桥的竖弯刚度评估一直是桥梁动力学研究的一个热点问题.基于斜拉桥中拉索对桥面梁起弹性支承作用的受力特点，针对漂浮式独塔斜拉桥竖弯刚度评估问题建立了一个新的评估方法：建立漂浮式独塔斜拉桥新的三梁离散弹簧整体动力学模型，以及相应动力学理论，利用传递矩阵法进行求解，从而对漂浮式独塔斜拉桥的竖弯刚度进行评估.在三梁离散弹簧模型中，将斜拉索视为无质量弹簧，将桥塔视为考虑轴力影响的欧拉柏努利梁，将桥面从与桥塔交接处截开为两根欧拉柏努利梁.最后通过算例分析和有限元计算结果的对比，表明本文提出的评估方法具有较高的精度和效率，可应用于工程设计中的计算和刚度评估.

斜拉桥；竖弯刚度；评估；建模；传递矩阵法

中国目前正处在大跨度桥梁建设的高潮期[1]，而斜拉桥以其优越的跨越能力，合理的受力体系，美观的结构形式，良好的经济性能，已成为现代桥梁工程中发展最快，最具竞争力的桥型[2]，并得到广泛应用[3].斜拉桥由于其跨度大和柔性斜拉索作为弹性支承的特点，使结构整体刚度较低，在动力方面有不同于一般工程结构的特殊性[4]，刚度不足是其主要问题[5].因此，斜拉桥竖弯刚度的正确计算和评估，对斜拉桥成桥安全起着至关重要的作用，也决定着斜拉桥的进一步发展.目前结构刚度评估主要有2种方法，一是基于对变形计算和测量的评估[6]；另一种是对结构自由振动周期或频率的分析[7].传统的计算结构自由振动周期或频率的方法主要是利用运动微分方程或者能量守恒原理，略去次要影响因素，得出近似计算公式，但这种方法进行模态形状分析相当困难.

一直以来,科学工作者和桥梁工作者都想找到一种既精确又方便的斜拉桥整体刚度的分析方法.除了通过有限元法建立全桥整体模型外，仅Cao等人[3]建立了刚性塔柔性梁式斜拉桥的整体动力学模型.该模型虽然能揭示斜拉桥整体的一些力学性能，但由于未计入塔的刚度影响，仍具有较大的局限性.由于斜拉桥整体结构复杂，兼有刚与柔耦合的特点，并且结构为高次超静定结构，建立整体动力学模型并对其进行理论分析相当困难.

经典传递矩阵法是20世纪20年代建立起来的用于研究弹性构件组成的一维线性系统振动问题的方法，在20世纪60～70年代的结构振动研究中被广泛应用[8].本课题组[9-13]基于传递矩阵法和对复杂结构动力学建模模型理论，对索拱结构的面内、面外振动、悬索桥、拱桥和斜拉梁的整体动力学进行了研究，为该类复杂结构的模态和参数分析，以及刚度评估建立了新的分析方法.Rosen等[14]建立了非线性传递矩阵法，用于对弯曲和扭转杆件的大变形进行了研究.Abbas等[15]应用有限元传递矩阵法研究了高温环境下变厚度壳的振动特性.目前，传递矩阵法由于其建模灵活、计算效率高等优点，已在诸多现代工程技术领域中得到了广泛应用[16].但是，针对斜拉桥这种伞形结构，其即非有规律的链式结构，也非真正意义上的平面结构，传递矩阵法虽具有很多优势，但也很难应用于斜拉桥的静动力学研究中.

综上所述，为了建立一种既精确又方便的斜拉桥整体刚度评估方法，本文拟基于对斜拉桥整体结构体系和受力特点的分析，针对漂浮式独塔斜拉桥建立适合于动力学分析的整体动力学模型，即三梁离散弹簧动力学模型.并基于该整体动力学模型建立斜拉桥整体竖弯刚度的基本计算理论和评估方法.

1 斜拉桥整体动力学模型

图1所示为一独塔斜拉桥成桥状态的常见立面构型.斜拉桥为高次超静定结构，桥面自重和荷载通过斜拉索传递给桥塔，再通过桥塔传递给地基和基础.在斜拉桥的受力体系中，斜拉索的主要作用是对桥面的弹性支承.在静力学方面，斜拉桥的受力非常清晰简洁，但对于斜拉桥的动力学问题，却相当复杂，特别是整体动力学行为的研究，至今也未找到一个真正意义上的全桥动力学模型.为评估斜拉桥的整体竖弯刚度，基于斜拉索起弹性支承作用的特点，可以忽略斜拉桥自身的局部振动(斜拉索的振动).因此，本文将斜拉索简化为一无质量弹簧，其质量可以平均分配到塔和梁的连接点上(本文暂时忽略其质量对整体刚度的影响).独塔斜拉桥的成桥立面构型就可简化为如图2所示的整体力学模型.该模型仍无法对其进行求解，需要对其进行进一步处理.为方便动力学问题的求解和分析，本文将桥面梁在与桥塔相交处截开分为两根梁，分别记作梁1和梁2.同时，将塔同样视为一根考虑轴力影响的欧拉柏努利梁，记为梁3.将梁1和梁2分别旋转至与梁3平行，则斜拉桥整体力学模型可进一步简化为如图3所示的三梁离散弹簧模型.该模型简单易懂，受力明确，并将原来的伞形体系变为链式体系，便于采用传递矩阵法进行求解.至此，本文首次建立了真正意义上的斜拉桥整体力学模型.通过该模型考虑边界条件，可以对成桥整体刚度进行分析计算.

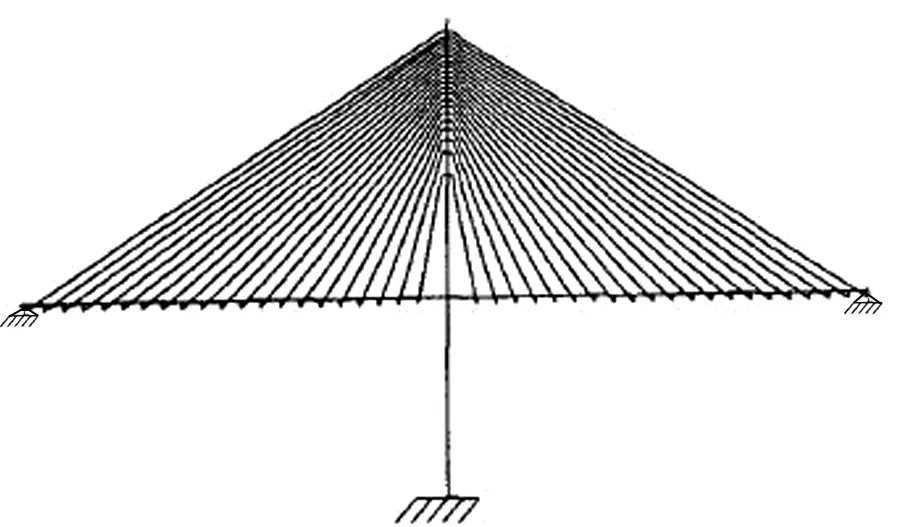
图1 斜拉桥成桥状态立面示意图Fig.1 Elevation sketch of complete state of cable-stayed bridge

图2 斜拉桥成桥状态力学模型Fig.2 Mechanical model of complete state of cable-stayed bridge

图3 三梁离散弹簧模型Fig.3 The dynamic model of three beams with discrete springs

2 斜拉桥整体动力学理论

为建立斜拉桥的动力学控制微分方程，做如下基本假设：1)梁和塔均为细长结构(截面高跨比小于0.1)；2)不计索的垂度和质量，将拉索简化为如图2所示的无质量弹簧；3)忽略塔自身重力产生的轴力影响；4)记入拉索初张力对梁轴力的影响；5)假定梁为漂浮式，即桥面和塔无接触.在此假定的前提下，本文模型和理论适用于斜拉桥成桥状态竖弯刚度的评估.为便于表示，分别建立各梁的坐标系如图2所示.分别用坐标x，y表示整体坐标，用坐标x1，x2和x3表示梁的轴向坐标，用w1，w2和w3分别表示三梁横向动位移，长度分别分L1，L2和L3.由于梁1与2本为一根梁，因此根据连续条件，两梁连接处端点的状态向量应满足连续性假设，即两梁端横向位移、弯矩相等，转角、剪力互为相反数.为分析方便和便于考虑轴力对梁的影响，将三梁分别根据索的数量n分成n+1段，其长度分别为l1,i，l2,i和l3,i(i=1,2,3,…,n+1)，弹簧的刚度分别为ki(i=1,2,3,…,n).则整个斜拉桥的势能可以表示为：

(w1,icosθi-w3,isinθi)2+

(w3,isinθi-w2,icosθi)2+

(w1,icosθi-w3,isinθi)+

(w3,isinθi-w2,icosθi)

(1)

式中:

kn+1=Pn+1=0

(2)

动能可以表示为:

(3)

由哈密尔顿变分原理,得

(4)

可得斜拉桥整体自由振动的动力学控制微分方程：

(w1,icosθi-w3,isinθi)cosθi+

(5)

(w3,isinθi-w2,icosθi)cosθi-

(6)

(w1,icosθi-w3,isinθi)sinθi+

(w3,isinθi-w2,icosθi)sinθi-

(7)

式中：Tm,i和Pi分别为梁和索的初始轴力；Xm,i为拉索作用位置；θi为斜拉索与塔的夹角；ρm,iAm,i和Em,iIm,i分别为梁单位长度的质量和梁横截面抗弯刚度.

至此，本文首次建立了飘浮式独塔斜拉桥的整体自由振动的动力学控制微分方程，将在下一节中对其进行求解.

3 传递矩阵法求解

由方程(5)至(7)可知，斜拉桥的整体自由振动方程相当复杂，对此进行理论求解相当困难.因此，将斜拉桥的每段梁分开考虑，弹簧作用通过端点条件考虑，应用传递矩阵法进行求解.

各段梁的运动方程简写为：

(8)

采用传递矩阵法计算斜拉桥竖弯自由振动时的频率.为便于进行分析和编程计算，将斜拉索作用位置考虑为节点，其余梁段考虑为等截面梁，变截面梁可通过细化梁段加以考虑.

令

wi(xi,ti)=wi(xi)qi(ti)

(9)

代入式(8)有：

(10)

化简后，得

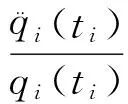
(11)

令

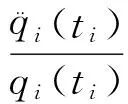
(12)

改写为：

(13)

(14)

则有：

(15)

式(15)的解为：

qi(ti)=Aisin(ωiti+θi)

(16)

综合式(11)(12)(14)，可得到：

(17)

令

(18)

式(17)可写为：

(19)

其通解为：

wi(xi)=Di,1sin(αixi)+Di,2cos(αixi)+

Di,3sinh(βixi)+Di,4cosh(βixi)

(20)

其中：

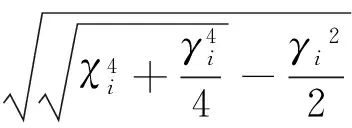
(21)

进而有：

Di,3βicosh(βixi)+Di,4βisinh(βixi)

(22)

(23)

(24)

根据力和位移的关系及平衡关系，可求得转角、弯矩、剪力分别为：

θi(xi)=Di,1αicos(αixi)-Di,2αisin(αixi)+

Di,3βicosh(βixi)+Di,4βisinh(βixi)

(25)

(26)

(27)

同理，将以上关系应用于梁的另一部分和塔.对梁有：

(28)

(29)

(30)

(31)

如果结构是对称的，模态有正对称和反对称之分，由于正对称模态时，索塔发生的是轴向运动，与反对称模态不同，所以对于索塔，这里要分情况讨论：

3.1 反对称模态

(32)

(33)

(34)

(35)

将式(20)，(25)～(35)分别用矩阵表示为：

ti=TiCi

(36)

其中:

(37)

(38)

Ti为15×15的矩阵，如式(39)所示.其中的一些表达式如下：

si,1=sin(αixi),ci,1=cos(αixi),si,2=sinh(βixi),

(39)

3.2 对称模态

正如前文所说，对称模态时索塔的运动为轴向运动，应将索塔等效为只发生轴向振动的梁.其运动微分方程可写为：

(40)

该方程的解为：

(41)

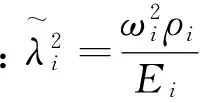
(42)

进而有：

(43)

主梁的运动方程和反对称模态相同，采用同样的处理方法，可以写出以下关系：

ti=TiCi

(44)

其中：

(45)

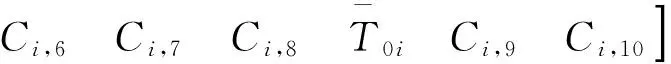
(46)

Ti如式(47)所示.

(47)

这里有：

si,1=sin(αixi),ci,1=cos(αixi),si,2=sinh(βixi),

现在来求Ci，对于任意一段i,当坐标xi=0(i=1,2,3,…)时,有

(48)

所以

(49)

式中：ti和ti,0分别为第i段的左边和右边状态向量.

(50)

(51)

(52)

(53)

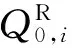
(54)

图4 斜拉索作用点处受力图Fig. 4 Internal force of anchorage point of cable-stayed bridge

(55)

(56)

(57)

(58)

(59)

(60)

(61)

(62)

(63)

(64)

将式(50)～(64)写成矩阵形式:

(65)

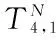
(66)

(67)

式中:

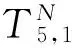
将式(49)代入式(65)中，可以得到:

(68)

最后,对整个斜拉桥，有

(69)

式中：

(70)

T为总传递矩阵，且对于非对称模态有：

(71)

(72)

对于对称模态有：

(73)

t1,0=

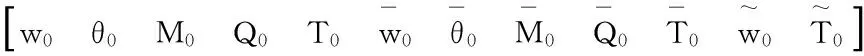
(74)

对于式(69)，应用边界条件，可改写为：

(75)

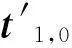
Δ=detT′=0

(76)

式(76)即为系统特征方程，由上述特征方程采用频率搜索法可解出斜拉桥自振频率.特征方程为圆频率的函数，不妨记为Δ(ω)，所谓频率搜索法是指给定圆频率一个很小的初值ωL=ω0，再给定圆频率一个微小的增量Δω.令ωR=ω0+Δω，如果这时候Δ(ωL)·Δ(ωR)<0，说明有零点存在，当Δω足够小时，取[Δ(ωL)+Δ(ωR)]/2作为零点，并把ωR的值赋给ωL，ωR则增加一个步长，继续寻找下一个零点；如果Δ(ωL)·Δ(ωR)>0，则把ωR的值赋给ωL，ωR增加一个步长，直至Δ(ωL)·Δ(ωR)<0.重复以上步骤，可以求出多阶自振频率f.该方法简单、方便、容易理解，便于采用MATLAB编程进行计算.

4 实例分析

4.1 工程概况

以长沙某铁路斜拉桥为例进行整桥竖弯刚度的评估.长沙某铁路斜拉桥结构形式为112 m+80 m+32 m非对称独塔双索面预应力混凝土槽形梁斜拉桥.塔柱总高79 m，桥面以上高45 m，共有4×8对斜拉索，左边相邻索之间的水平距离为12.8 m，右边相邻索之间的水平距离为9 m，塔柱上相邻索之间的距离为2.5 m，斜拉索采用Φ7 mm高强度低松弛镀锌平行钢丝.

4.2 计算结果对比分析

采用本文模型和理论建立的MATLAB程序计算出的模态频率和用ANSYS计算出的结果进行比较.表 1给出了飘浮式单塔斜拉桥成桥状态下的自振频率.比较分析可以看出，用本文模型和理论计算的自振频率与ANSYS建模计算的自振频率之间的误差很小，最大误差的绝对值没有超过3.57%.这证实了本文建立的漂浮式单塔斜拉桥成桥竖弯刚度评估的理论和方法的正确性和适用性.而且第1阶固有频率的误差只有2.22%，这对结构的初频设计，定量和定性分析，以及对结构基本刚度进行评估均具有非常高的精度.由此说明，本文建立的飘浮式单塔斜拉桥整体动力学模型和理论，以及求解方法具有较好的精度和工程应用价值.

表1 斜拉桥整桥自振频率对比表

表2给出了考虑索塔自身重力产生的轴力影响时，斜拉桥整桥自振频率对比表.表2中，ANSYS计算出的自振频率考虑了索塔重力的影响，而本文方法计算出的频率没有考虑索塔重力影响.通过相对误差一栏可知，索塔重力对自振频率的影响很小，最大误差绝对值只有3.63%，这说明可以忽略索塔重力对斜拉桥自振频率的影响，与本文在第2节中所提出的假设相符.当然，为计算更为精确，在计算中也可以考虑塔自身重力的影响.

应用本文的方法、理论和程序，对于该类桥型的动力学问题可以进行全面的参数分析，还可进行精细化计算：如对桥面梁、塔变截面的考虑、拉索刚度、倾角等变化的分析.另外，对于斜拉桥施工过程中竖弯刚度的评估，由于塔梁采用临时固结的措施，本文建立的计算模型不适用于施工阶段的评估分析.对于斜拉桥施工过程的竖弯刚度评估，将在下一阶段的工作中进行研究.

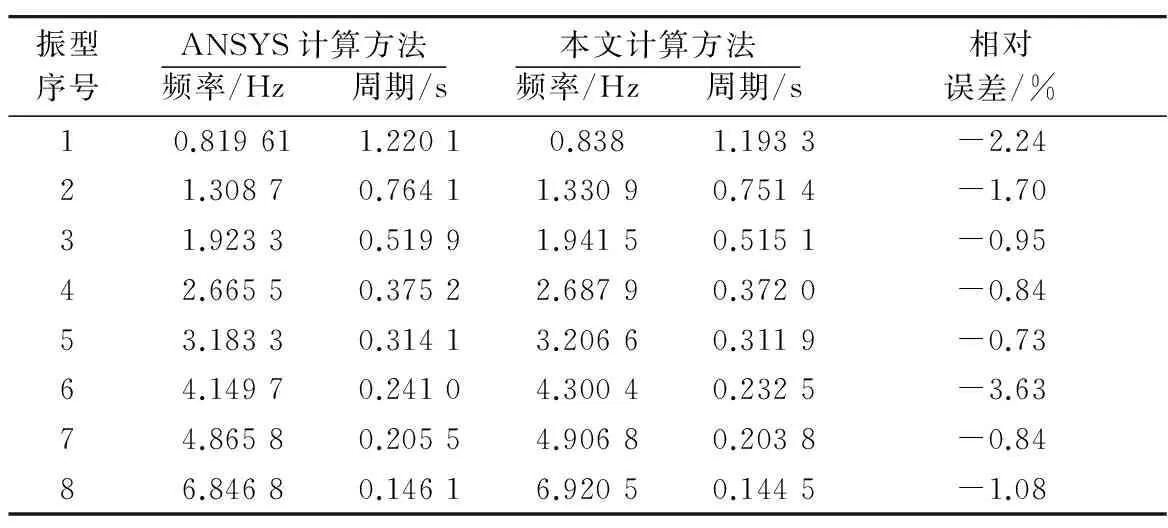
表2 考虑索塔重力斜拉桥整桥自振频率对比表

5 结 论

本文针对斜拉桥的整体刚度评估问题，克服了斜拉桥整体动力学模型建立的困难，通过对漂浮式独塔斜拉桥结构体系和受力特点的定性分析，首次建立了该种桥型的三梁离散弹簧整体动力学模型.基于传递矩阵原理，推导得到了飘浮式独塔斜拉桥结构竖弯刚度评估计算的基本理论.以长沙某铁路斜拉桥为研究对象，对独塔斜拉桥的成桥刚度进行了评估分析.研究结果表明，本文提出的飘浮式独塔斜拉桥三梁离散弹簧整体动力学模型及相应理论，以及采用传递矩阵法进行计算分析的整桥竖弯刚度评估方法具有较高的精度和效率，对该类型桥梁的成桥刚度评估具有重要的科学意义和工程应用价值.

[1] 祝志文,陈魏,向泽,等. 大跨度斜拉桥主梁气动力特性的大涡模拟[J]. 湖南大学学报: 自然科学版,2013,40(11):26-33.

ZHU Zhiwen,CHEN Wei,XIANG Ze,etal. Large eddy simulation of aerodynamics on main girder of long span cable-stayed bridges[J]. Journal of Hunan University: Natural Sciences,2013,40(11): 26-33.(In Chinese)

[2] 邓露,王维.公路桥梁动力冲击系数研究进展[J].动力学与控制学报,2016,14(4):289-300.

DENG Lu,WANG Wei. Research progress on dynamic impact factors of highway bridges[J].Journal of Dynamics and Control,2016,14(4): 289-300.(In Chinese)

[3] CAO D Q,SONG M T,ZHU W D,etal. Modeling and analysis of the in-plane vibration of a complex cable-stayed bridge [J]. Journal of Sound and Vibration,2012,331: 5685-5714.

[4] 黄平明,刘旭政.独塔斜拉桥在不同边界条件下的动力特性分析[J]. 公路,2007(8): 1-4.

HUANG Pingming,LIU Xuzheng. Dynamic characteristics analysis of cable-stayed bridges with single tower under various boundary conditions[J]. Highway,2007(8): 1-4.(In Chinese)

[5] 曹珊珊.多塔斜拉桥的刚度参数分析与安全性研究[D].北京:北京交通大学土木建筑工程学院,2012: 5-7.

CAO Shanshan. Stiffness parameters analysis and security research of multi-pylon cable-stayed bridge [D]. Beijing: School of Civil Engineering,Beijing Jiaotong University,2012: 5-7.(In Chinese)

[6] 王海城,舒绍云,熊涛.某矮塔斜拉桥主梁变形分析与评定[J].工程质量,2013,31(7): 42-44.

WANG Haicheng,SHU Shaoyun,XIONG Tao. Analysis of an extradosedcable-stayed bridge girder deformation[J]. Construction Quality,2013,31(7): 42-44.(In Chinese)

[7] 黄斌,李烨君,朱礼平,等.桥塔抗弯刚度随机性对斜拉桥动力特性的影响[J].西南交通大学学报,2014,49(2): 202-207.

HUANG Bin,LI Yejun,ZHU Liping,etal. Effects of towers’ random sectional bending stiffness on dynamic characteristics of large-span cable-stayed bridge[J]. Journal of Southwest Jiaotong University,2014,49(2): 202-207.(In Chinese)

[8] 万浩川,李以农,郑玲.改进的结构振动传递矩阵法[J].振动与冲击,2013,32(9): 173-177.

WAN Haochuan,LI Yinong,ZHENG Ling. Improved transfer matrix method in structural vibration analysis[J]. Journal of Vibration and Shock,2013,32(9): 173-177.(In Chinese)

[9] ZHAO Y Y,KANG H J. In-plane free vibration analysis of cable-arch structure[J]. Journal of Sound and Vibration,2008,312: 363-379.

[10] KANG H J,ZHAO Y Y,ZHU H P. Out-of-plane free vibration analysis of a cable-arch structure[J]. Journal of Sound and Vibration,2013,332: 907-921.

[11] WANG Z Q,KANG H J,SUN C S,etal. Modeling and parameter analysis of in-plane dynamics of a suspension bridge with transfer matrix method[J]. Acta Mech,2014,225: 3423-3435.

[12] KANG H J,XIE W D,GUO T D. Modeling and parametric analysis of arch bridge with transfer matrix method[J]. Applied Mathematical Modelling,2016,40: 10578-10595.

[13] 康厚军,解维东,郭铁丁.CFRP索斜拉梁面内自由振动建模及参数分析[J]. 湖南大学学报: 自然科学版,2016,43(9):18-25.

KANG Houjun,XIE Weidong,GUO Tieding. Modeling and parameters analysis on in-plane free vibration of cable-stayed beam[J]. Journal of Hunan University: Natural Sciences,2016,43(9): 18-25.(In Chinese)

[14] ROSEN A,GUR O. A transfer matrix model of large deformations of curved rods[J]. Computers and Structures,2009,87: 467-487.

[15] ABBAS L K,MA L,RUI X T. Natural vibrations of open-variable thickness circular cylindrical shells in high temperatureeld[J].Journal of Aerospace Engineering,2010,23(3): 205-212.

[16] 宋文.三种升速条件下的鱼雷涡轮机转子系统动力学特性[J].动力学与控制学报,2016,14(3):235-240.

SONG Wen. Dynamic properties of torpedo turbine rotor system in three speed-up processes[J]. Journal of Dynamics and Control,2016,14(3):235-240.(In Chinese)

A New Method for Vertical Bending Stiffness Evaluation of Floating Single-tower Cable-stayed Bridge

KANG Houjun1†,SU Xiaoyang1,GONG Ping2,CAI Xiangyang2,LIU Haibo3,HU Jianhua3,GUO Tieding1

(1.College of Civil Engineering,Hunan University,Changsha 410082,China;2.Provincial Ruchen Highway Construction Development Co Ltd,Chenzhou 423000,China;3.Hunan Provincial Communications Planning,Survey & Design Institution,Changsha 410008,China)

The vertical bending stiffness assessment of the cable-stayed bridge has been a hot research issue in the dynamics of bridge. Based on the mechanical characteristics of stay cable supporting deck，a new evaluation method was proposed for the vertical bending stiffness of a floating single-tower cable-stayed bridge. Firstly，a new dynamic model (i.e.，triple-beam with discrete springs) of the floating single-tower cable-stayed bridge was proposed and its corresponding dynamics theory was derived. In the proposed model，the stay cables were simplified as springs without mass and the single-tower was regarded as an Euler-Bernoulli beam with consideration of axial force. At the same time，the deck was divided into two segments at its intersection with tower，hence the deck was regarded as two Euler-Bernoulli beams. The eigenvalue and eigenvector of the dynamic system were then solved by the transfer matrix method，which was used for the evaluation of vertical stiffness of the floating single-tower cable-stayed bridge. Finally，the case study and its comparison with results obtained by the finite element method show that the evaluation method proposed is of high precision and efficiency，and can be used for the calculation and stiffness evaluation in engineering design.

cable-stayed bridge；vertical bending rigidity；evaluation；modeling；transfer matrix method

O343.9

A

1674-2974(2017)11-0126-09

10.16339/j.cnki.hdxbzkb.2017.11.015

2016-10-29

国家自然科学基金资助项目(11572117，11502076)，National Natural Science Foundation of China(11572117，11502076)

康厚军(1977-)，男，四川安岳人，湖南大学副教授，博士

†通讯联系人，E-mail：khjun@hnu.edu.cn