基于MIDAS/Gen的槽式聚光器结构模态分析

李正农，李廉洁，吴红华

(1.湖南大学 土木工程学院，湖南 长沙 410082；2.湖南省电网工程公司，湖南 衡阳 421000)

基于MIDAS/Gen的槽式聚光器结构模态分析

李正农1†，李廉洁2，吴红华1

(1.湖南大学 土木工程学院，湖南 长沙 410082；2.湖南省电网工程公司，湖南 衡阳 421000)

针对槽式聚光器结构优化问题，根据张家港试验基地槽式聚光器实体装置，基于MIDAS/Gen建立槽式聚光器三维有限元模型，采用Lanczos模态计算方法，进行各角度工况下模态分析，得到槽式聚光器在不同工况下的结构模态特征.对槽式聚光器装置进行动力特性测试，测点布置在结构的多个位置，传感器主要布置在聚光镜的镜面中心位置.现场实测过程中选用优泰公司的软件和设备——动态信号采集系统、传感器以及采集仪等试验设备和装置，获取各测点的有效数据，通过优泰软件对原始数据进行处理，得到槽式聚光器装置的动力特性.将数值计算结果与原型实测结果进行对比验证，验证结果表明：本文建立的槽式聚光器三维有限元模型能够较好地模拟现有槽式聚光器结构，能够用于槽式聚光器的静态分析及结构优化分析研究，可以为进一步提高槽式聚光镜组的聚光效果和降低成本提供参考.

槽式聚光器；模态分析；有限元方法；MIDAS/Gen

太阳能热发电系统主要有塔式(Tower Style)[1]、碟式(Dish Style)[2-3]和槽式(Groove Style)[4-5]3种.槽式聚光系统(Groove-type Condenser Solar System)是近年来发展起来的、具有较好商业化基础的聚光系统[6-7]，广泛应用于太阳能集热技术及太阳能热发电技术.槽式聚光器利用桁架结构支撑起玻璃反射镜形成一个曲面结构，配备辅助装置使得其随太阳转动，达到充分利用太阳能的目的，构成一个完善的柱面聚光系统(Cylindrical Condenser System).目前，槽式聚光系统的应用在国外已形成一定规模，并实现了商业化，但在国内尚处于起步阶段.

槽式聚光系统一般包括：太阳能聚光系统、能量接收系统和太阳运动追踪系统[8].其中，太阳能聚光系统的成本通常占整个发电系统成本的一半以上[9].由于太阳能聚光系统的迎风面积大、结构的整体刚度相对较低，风荷载是槽式聚光系统结构设计时的重要控制荷载，结构抗风性能是发电系统成本控制的关键因素[10-12].国外槽式太阳能热发电站通常建于无风和少风地带，但是，在我国太阳能充足的地区往往多风，甚至有较高频率和强度的沙尘暴[13].槽式聚光器结构与房屋结构有所不同，房屋结构主要研究其整体变形，因此注重分析其低阶频率.而槽式聚光器结构必须考虑其局部变形，因为局部变形会导致槽式聚光器的聚光效果变差，使得太阳能利用效率降低.高阶模态体现了槽式聚光器结构的局部变形情况，这对结构的抗风性能研究有较大帮助.在风荷载作用下，在某些频率区间，槽式聚光器结构局部可能发生较大变形.针对槽式聚光器开展模态分析的最终目的是识别出该系统的模态参数，为其结构系统的振动分析、振动故障诊断和预报，以及其结构动力特性的优化设计提供理论依据.因此，针对槽式聚光器的抗风性能和结构优化开展研究，具有一定的科学意义和工程应用价值.

1 槽式聚光器结构模型的建立

1.1 槽式聚光器结构的组成

本文以位于张家港试验基地的槽式聚光器装置为研究对象，图1所示为现场实物图.聚光器装置的设计主要考虑结构的刚度和强度，特别是结构的抗风性能要求，主体框架及镜面支架需满足支撑聚光镜并确保风荷载作用下的刚度和强度要求.

图1 张家港试验基地槽式聚光器装置Fig.1 Groove type condenser device in Zhangjiagang test site

本文研究对象主要为槽式聚光器主体结构，包括主体框架和支座、镜面支架、端板和聚光镜部分.本文研究的实体模型为2个6 m槽式聚光器通过连接装置(槽型钢和转动轴)组合在一起.聚光镜通过固定角支座与镜面支架连接，镜面支架与主体支架通过螺栓连接，固定在主体支座上.6 m槽式聚光器结构的主要参数见表1.

表1 6 m槽式聚光器结构主要参数

1.2 槽式聚光器结构模型的简化原则

槽式聚光器的主体结构主要由冷弯方管组成，主要分为主体支座、主体框架及镜面支架等部分，结构较为复杂.本文在建立有限元模型时，综合考虑建模准确度及便于进行有限元分析，对槽式聚光器的主体结构进行合理的简化.具体简化原则如下：

1)简化聚能管集热装置，简化转动和减速装置.聚能管和聚能管支架对槽式聚光器主体结构的抗风性能影响较小，因此简化处理.转动和减速装置的细部特征建模较复杂，且对整体结构的影响很微小，因此进行简化处理，忽略其细部特征.

2)保证有限元模型中的几何尺寸与实际模型的形状和尺寸一致，确保模型与现场实际模型的相似性，使其能真实反映结构的特征和力学性能.

3)忽略实际模型中的一些细微的特征，如螺栓、小孔、圆弧等.这些细微特征容易造成网格单元不规则，网格质量差，影响分析结果的精度.

1.3 模型的建立

1.3.1 聚光器结构模型

本文研究的聚光器结构由2个6 m槽式聚光器装置通过两根槽型钢和转动轴连接构成整体.6 m槽式聚光器装置主要由主体框架、镜面支架、主体支座、端板、转动轴和聚光镜组成.主体框架主要起到抗扭转和抗弯的作用，镜面支架连接镜面和主体框架，起到固定镜面的作用.端板和转动轴连接主体框架和主体支座，实现主体框架固定在主体支座上的作用.主体框架、镜面支架和主体支座之间主要通过螺栓连接，螺栓连接方便各部件的拆装，可随时更换.

主体框架为一个空间三棱柱体钢结构，底面为一个等腰三角形，钢结构由2种规格的方管组成，规格不同、长度不一的方管通过焊接方式连接成整体.端板为钢板.镜面支架采用方管焊接而成.镜面支架之间通过4根横撑连接固定.主体支座采用2种规格的方管焊接而成.本文探讨的结构为2个6 m槽式聚光镜通过2根槽型钢管连接成的整体.槽型钢管尺寸为80 mm×43 mm×5 mm.

1.3.2 聚光镜模型

聚光镜截面形状为抛物面镜，镜面略有弧度，但由于聚光镜的弧度很小，且对结构的分析影响较小，因此本文的有限元模型忽略其弧度，采用平面镜进行分析.镜面开口宽度为5 958 mm，整个6 m槽式聚光镜镜面组合的长度方向为6 204 mm.聚光镜沿长度方向和宽度方向分别分布有6块聚光镜，每块聚光镜的尺寸为1 000 mm×1 000 mm，镜面沿长度方向间距为20 mm，沿宽度方向为30 mm，且中间部分间隔为200 mm.每块聚光镜有4个镜面支座与镜面支架相连，固定在镜面支架上.将聚光镜安装在聚光器钢结构上，即得到完整的槽式聚光器装置，如图2所示.

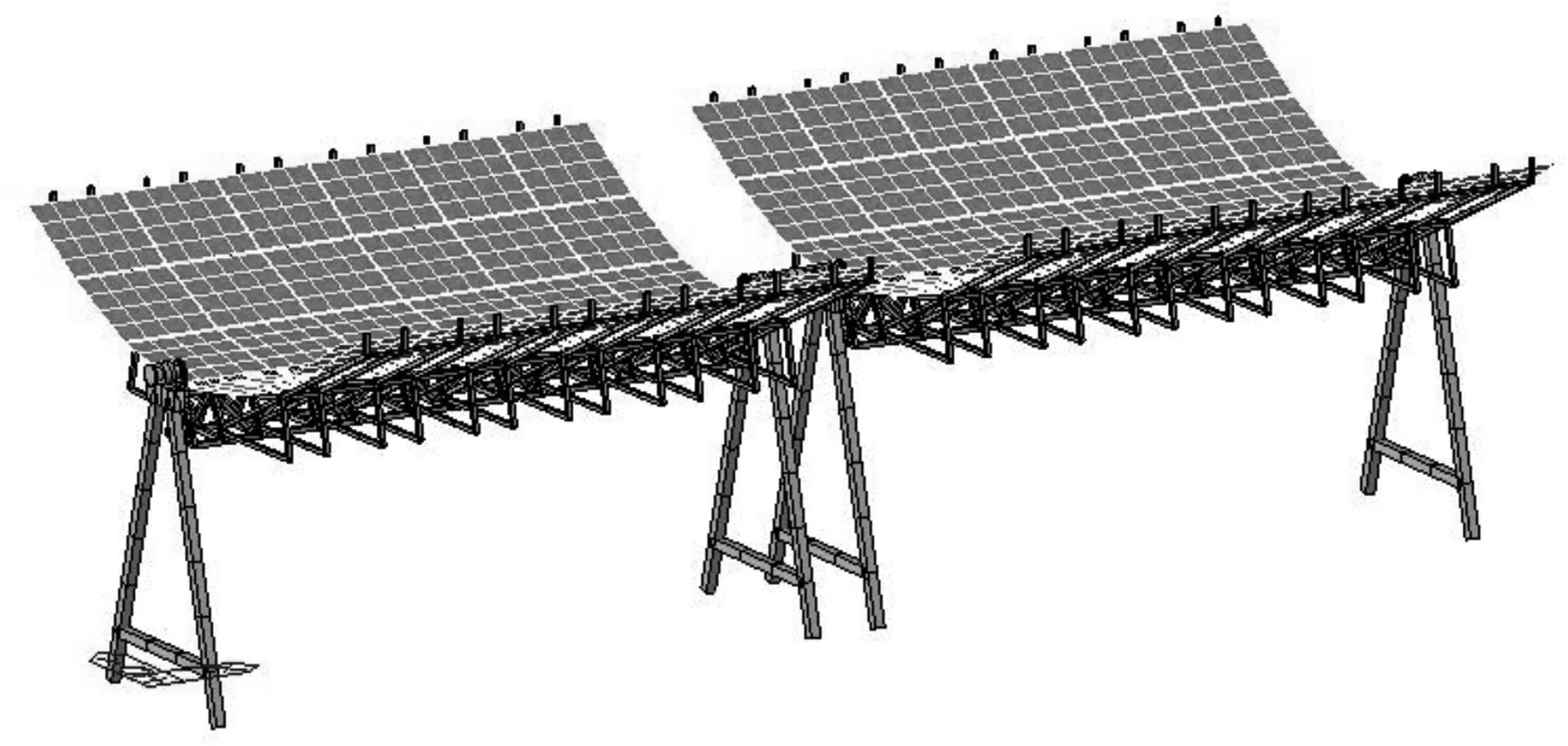
图2 槽式聚光器结构有限元模型Fig.2 The finite element model of groove type condenser

1.4 聚光器结构有限元模态分析前处理

1.4.1 几何模型处理

进行模态分析前，需要简化一些对模态分析结果影响很小的细节，如倒角、圆角、螺栓等部位.同时，聚能管和聚能管支架对于聚光器结构而言，质量和刚度均较小，对聚光器结构的荷载分布和刚度影响很小，且本文主要研究主体框架和镜面支架的性能及优化，故在有限元模型中予以忽略.

1.4.2 网格划分

本文研究的聚光器结构为2个6 m槽式机通过600 mm长的槽型钢和转动轴连接在一起，形成一个整体的槽式聚光器装置.整个聚光镜结构装置长约13 m，镜面组合结构开口宽度达5 958 mm，聚光镜的厚度为4 mm，其余支架部位多采用尺寸和规格不一的冷弯空心方管钢结构.根据相关软件和模型处理经验，采取经验划分网格的方法.根据各部分结构的尺寸特点，综合考虑计算精度与效率，最终划分结果：单元数为3 505个，结点为3 032个.

1.4.3 材料属性定义

本文研究的聚光器结构装置的钢结构部分均采用Q235钢材，聚光镜的材料为特制钢化玻璃.本文主要探讨聚光器结构装置的弹性形变和模态等基本性能，因此，应当在有限元分析软件MIDAS/Gen中对材料的各项性能进行定义，如表2所示.

1.4.4 边界条件定义

本文研究的聚光器结构在驱动装置和减速装置的共同作用下绕轴转动，根据太阳光照射的方向进行调整.这里主要考虑结构的边界条件的定义.整体的聚光器结构由2个6 m槽式机组成，支座底部与地相连，这里采取约束6个自由度的一般支承.对于主体支座与端板和转动轴的连接，即镜面支架转动的部分，采用弹性连接，镜面支架与主体支座能发生相对转动.主体框架和镜面支架部分的螺栓连接，采用刚性连接.聚光镜面与镜面支架部分的支座连接简化为刚性连接并释放板端约束.

表2 材料的力学参数

1.5 模态分析理论基础

本文的模态计算采用Lanczos法[14]，其基本思想是通过正交转换将对称矩阵转换为三对角矩阵，这种方法实际上是Arnoldi算法对于对称矩阵的一种特殊算例.n自由度的槽式聚光镜结构风致响应的控制方程可写为：

(1)

式中：M，C，K分别是结构的质量、阻尼和刚度矩阵；y和F(t)分别是结构的位移响应向量和脉动风荷载向量.上述方程可以下列坐标变换进行缩减：

y=D·x.

(2)

式中：D是以s个Lanczos向量为列的n×s阶矩阵，通常s远小于n：

D=[φ1,φ2,φ3,…,φs].

(3)

Lanczos向量φ1的生成算法由下列递推过程获得：

(4)

(5)

(6)

βj=(φj-1T·M·rj-1)0.5,

(7)

(8)

结合式(4)和式(8)，式(5)可写成：

(9)

上式可联合写为：

K-1·M·D=D·T.

(10)

利用正交性DT·M·D=I，对左式乘以DT·M可得到：

DT·M·K-1·M·D=T.

(11)

其中，T是s×s的三对角矩阵.而脉动风荷载向量可以使用POD法分解成如下形式：

(12)

如前所述，由于空间位置是本征模态的决定性因素，且第一阶本征模态表示的脉动风压能量占有很大份量，因此，可将第一阶本征模态作为空间向量，生成第一个Lanczos向量，即：

r0=K-1·φ.

(13)

2 聚光器结构有限元模态分析结果

对聚光器结构模型进行前处理后，对槽式聚光器装置整体进行有限元模态分析及求解，分别得到了竖向角为0°，30°，45°，60°和90°时，槽式聚光器装置的结构动力特性(固有频率和振型).限于篇幅，下文中仅给出竖向角为0°和45°时的结果.

2.1 竖向角为0°时的结构模态结果

表3中给出了竖向角为0°时，槽式聚光器结构的模态分析结果，图3给出了竖向角为0°时，槽式聚光器结构的不同阶模态振型计算结果.

表3 竖向角0°时聚光器结构模态分析结果

结合第一阶至第十阶的频率和振型图来看，第一阶和第二阶、第四阶和第五阶、第六阶和第七阶，以及第八阶和第九阶的频率非常相近，且振型图呈正对称与反对称的关系.

第一阶、第二阶和第六阶、第七阶振型图以槽式聚光镜绕转动轴转动为主，第一阶和第七阶振型图呈正对称：第一阶振型图为左右两侧槽式聚光镜均向下转动；第七阶振型图为上下两侧聚光镜均绕转动轴向内转动(收紧).第二阶、第六阶振型图呈反对称：第二阶振型图为左侧向上转动，右侧向下转动；第六阶振型图为左侧绕转动轴向外转动(张开)，右侧则向内转动(收紧).第三阶振型图以X向平动为主.第四阶、第五阶，以及第八至十阶振型图以扭转为主，扭转形态多为局部变形.其中，第四阶、第八阶、第十阶振型图沿Y轴正对称；第五阶、第九阶振型图沿Y轴反对称.

图3 聚光器结构模态振型(竖向角0°)Fig.3 Modal vibration modes of groove type condenser (vertical angle 0°)

2.2 竖向角为45°时的结构模态结果

表4中给出了竖向角为45°时，槽式聚光器结构的模态分析结果，图4给出了竖向角为45°时，槽式聚光器结构的不同阶模态振型计算结果.

表4 竖向角45°时的模态结果

结合第一阶至第十阶的频率和振型图来看，第一阶和第二阶、第四阶和第五阶、第六阶和第七阶，以及第八阶和第九阶的频率非常相近，且振型图呈正对称与反对称的关系.

第一阶、第二阶和第六阶、第七阶振型图以槽式聚光镜绕转动轴转动为主，第一阶和第七阶振型图呈正对称：第一阶振型图左右两侧槽式聚光镜均向上转动；第七阶振型图上下两侧聚光镜均向外转动(张开).第二阶和第六阶振型图呈反对称：第二阶振型图为左侧向下转动，右侧向上转动；第六阶振型图左侧聚光镜上下两侧绕转动轴向内转动(收紧)，右侧聚光镜上下两侧均向外转动(张开).第三阶振型图以X向平动为主.第四阶、第五阶，以及第八至十阶振型图以扭转为主，扭转形态多为局部变形.第四阶、第八阶、第十阶振型图沿Y轴正对称；第五阶、第九阶振型图沿Y轴反对称.

2.3 有限元模态结果分析

根据以上有限元模态分析结果，得到以下结论：

1)整个聚光器结构由2个6 m槽式机组成，模态分析结果往往呈现一定的对称规律，同一相近频率下的振型呈现正对称和反对称，成对出现.

2)按照竖向角0°, 30°, 45°, 60°和90°五个主要角度来分别计算槽式聚光镜不同工况下的整体模态情况.不同竖向角度下，虽然结构的质量和刚度都没变，但竖向角度不同，结构的质量分布与重心发生了变化，结构的模态中固有频率和振型有一定的变化.同时，第一阶至第十阶的频率范围均为2～6 Hz，且对应各阶固定频率较接近，对应振型图形态类似.

图4 聚光器结构模态振型(竖向角45°)Fig.4 Modal vibration modes of groove type condenser (vertical angle 45°)

3)分析不同竖向角度的模态对后文的分析有重要意义，对模型安全角度和最不利角度的确定和分析具有指导作用.不同竖向角工况下，模态振型图与槽式聚光器结构在荷载作用下的位移形变情况有一定联系.模态分析结果揭示了结构的动力特性，对槽式聚光器结构的抗风性能研究和结构优化具有重要意义.

3 模态分析结果的验证

利用有限元软件进行上述模态分析，得到了槽式聚光器装置的结构动力特性(固有频率和振型).由于现场原型实测方法常能较准确地获取结构的动力特性，因此，利用实测模态与前文有限元模态分析成果进行对比论证.

对位于江苏省张家港市试验基地的槽式聚光器装置进行的动力特性测试中，测点布置在结构的多个位置，传感器主要布置在聚光镜的镜面中心位置.现场实测过程中选用优泰公司的设备和软件——动态信号采集系统和传感器，以及采集仪等试验设备和装置.依次采集各个测点的有效数据，并通过优泰软件对原始数据进行处理，得到了槽式聚光器装置的动力特性.

3.1 模态实测概况

本文进行现场实测的原型是位于张家港试验基地的聚光器结构.该聚光器上部结构主要由72块镜面板、空间桁架、横轴等构成，其中镜面部分总面积约为72 m2，底部支撑为钢立柱，类似A字型，参见图1.实际测试中，对上部结构和立柱分别进行了模态测试，分为竖向角0°, 30°, 45°, 60°和90°五种工况.在每一种工况中，对于上部镜面板进行了垂直于镜面方向的测试，对底部支撑立柱进行了水平面内的2个方向的测试，每组测试时间约为2 min.

激励方案：由于本次实测结构原型尺寸庞大、造型较复杂、不易人工激励，传统的激振器法和锤击法的效果不好.同时由于实物位于空旷的场地中，受环境影响较大，所以最终决定采用环境激励的方式.环境激励具有以下优点：节约成本；不会使结构产生局部损伤；简捷而又满足真实的边界条件.环境激励作为一种天然的激励形式，已在许多大型工程结构中得到应用.

测点布置方案：在实际测试中，选择了一个测点作为参考点，并保持参考点位置的传感器不动，多次移动其他测点处的传感器，以达到测试全部测点处数据的目的.为了使测得的模态数据更加准确，同时避免丢失部分模态，需要尽可能多地布置测点，并且测点的位置要选择正确，即把加速度传感器布置在合适的地方.对于上部每块镜面板，选择在镜面板背面中心处布置一个测点，该位置有一定的代表性，振幅相对较大，有利于形成明显的振型图.共有72块镜面板，所以布置了72个测点.底部支撑方面，理论上认为立柱底部完全固定于地面，所以每根立柱上共有3个测点，分别位于其顶部和两斜边的中点处，共有4根立柱，所以布置了12个测点.整个结构为84个测点.

数据采集相关设备：数据采集仪为武汉优泰电子技术有限公司生产的UT3300系列数据采集器.传感器采用约克仪器公司的4000型加速度计.参照聚光器结构有限元模态分析结果，可发现前10阶的最大频率不超过9 Hz，故本次实测的采样频率选择为fs=128 Hz，满足香农采样定理fs≥2.56fc(fc为信号的截断频率).

模态分析软件：本试验采用武汉优泰电子技术有限公司的uTekMa模态分析软件.通过在软件中建模并导入实测采集的数据，再进行处理分析，即可得到模态参数、振型图等想要的结果.其中模态验证主要是通过模态相关性检验(MAC)、模态比例因子检验(MSF)以及振型空间相关性检验(COMAC).

3.2 竖向角为0°时的模态结果对比

表5为该模型0°竖向角下，前九阶有限元模拟对应于前三阶现场实测得到的固有频率对比和相对误差.优泰软件分析得到的模态，结构固有频率仅有3位小数，因此有限元计算同样取3位小数，固有频率对比分析如表5所示.

表5 竖向角0°时槽式聚光器装置固有频率对比

图5至图7为该模型前九阶有限元模型的振型(第三阶振型图以X向平动为主，而模态实测时由于加速度传感器没有布置在X方向,所以实测结果与有限元计算结果的第三阶振型不进行对比)与前三阶实测模型的对比图，图5至图7中(a)和(b)均为有限元模型分析得到的振型图，(c)为现场实测分析得到的振型图.有限元模型一阶和二阶、四阶和五阶、六阶和七阶、八阶和九阶的频率分别非常接近，且振型图分别为正对称和反对称，因此可把频率非常接近的两阶分为一组.而现场实测由于条件有限，无法测得平动模态，且存在一定的误差，只能测出部分振型图，在对应的六阶和七阶出现了模态丢失.

从图5至图7中可看出，有限元模型分析得到的第一、二阶振型图对应于现场实测分析得到的第一阶振型；有限元模型得到的第四、五阶振型图对应于现场实测分析得到的第二阶振型图；有限元模型得到的第八、九阶振型图对应于现场实测分析得到的第三阶振型图.有限元模型与现场实测分析得到的对应固有频率的相对误差均在8%以内.因为现场实测存在模态丢失的风险，有限元模型分析得到的第六、七阶无对应的实测振型图.有限元模型得到的第一、二阶振型主要是结构绕横轴的转动，第四、五、八、九阶则主要是结构局部扭转.从有限元模型的振型图中还可发现，第一、四、八阶振型呈一定的正对称性，第二、五、九阶振型则呈一定的反对称性.现场实测得到的振型图均为正对称，说明实测过程中可能丢失了反对称的振型图.

图5 第一阶实测振型对比图(竖向角0°)Fig.5 Contrast figures of the first vibration modal(vertical angle 0°)

图6 第二阶实测振型对比图(竖向角0°)Fig.6 Contrast figures of the second vibration modal(vertical angle 0°)

图7 第三阶实测振型对比图(竖向角0°)Fig.7 Contrast figures of the third vibration modal(vertical angle 0°)

3.3 竖向角为45°时的模态结果对比

表6为该模型45°竖向角下，前九阶有限元模拟对应于前三阶现场实测得到的固有频率对比和相对误差.图8至图10为该模型前九阶有限元模型的振型(第三阶振型主要为平动，不参与对比)与前三阶实测模型的对比图，图8至图10中(a)和(b)均为有限元模型分析得到的振型图，(c)为现场实测分析得到的振型图.有限元模型一阶和二阶、四阶和五阶、六阶和七阶、八阶和九阶的频率分别非常接近，且振型图分别为正对称和反对称，因此可把频率非常接近的两阶分为一组.现场实测由于条件有限，无法测得平动模态，且存在一定的误差，只能测出部分振型图，在对应的六阶和七阶出现了模态丢失.

结合表6以及图8至图10，可看出，有限元模型分析得到的第一、二阶振型图对应于现场实测分析得到的第一阶振型图；有限元模型得到的第四、五阶振型图对应于现场实测分析得到的第二阶振型图；有限元模型得到的第八、九阶振型图对应于现场实测分析得到的第三阶振型图.有限元模型与现场实测分析得到的一一对应的固有频率值的相对误差均在8%以内.因为现场实测存在模态丢失的风险，故有限元模型分析得到的第六、七阶无对应的实测振型图.有限元模型得到的第一、二阶振型主要是结构绕横轴的转动，第四、五、八、九阶则主要是结构局部扭转.从有限元模型的振型图中还可发现，第一、四、八阶振型呈一定的正对称性，第二、五、九阶振型则呈一定的反对称性.现场实测得到的振型图均为正对称，说明实测过程中可能丢失了反对称的振型图.

图8 第一阶振型对比图(竖向角45°)Fig.8 Contrast figures of the first vibration modal(vertical angle 45°)

图9 第二阶振型对比图(竖向角45°)Fig.9 Contrast figures of the second vibration modal(vertical angle 45°)

图10 第三阶振型对比图(竖向角45°)Fig.10 Contrast figures of the third vibration modal(vertical angle 45°)

阶数频率/Hz有限元计算实测相对误差/%11.99722.0361.8751.8756.117.9143.84553.9083.6883.6884.085.6364.81174.812————85.54595.5505.5635.563-0.33-0.23

3.4 有限元模态验证结果分析

根据以上有限元模态分析与现场实测的模态结果对比，可得到以下结论：

1)和有限元模型的模态分析结果类似，不同竖向角工况下，现场实测得到的对应阶数的模态分析结果相似，即竖向角不同，对应的同阶固有频率非常接近，且振型图较为相似.

2)有限元模型与现场实测分析得到的振型图，均呈现出一定的对称性.有限元模型分析得到的振型图呈现正对称与反对称.现场实测丢失反对称振型图，只有正对称振型图.

3)现场实测得到的结构动力特性和有限元模拟分析得到的结果，吻合较好，对应各阶的固有频率相对误差在8%以内，对应的振型图相似.

4)有限元模型与现场实测得到的固有频率范围均在2.0～5.5 Hz区间内.

5)有限元模型得到的结果更为全面，而现场实测得到的模态出现一定程度的丢失.

4 结 论

槽式聚光镜组系统是近年来国际上最主流的太阳能聚光系统，在太阳能集热与发电方面已有较大规模的应用.本文介绍了有限单元法和模态分析的原理，并利用MIDAS/Gen软件对已有槽式聚光器进行数值模拟研究，获得了相应的模态分析结果.具体研究成果如下：

1)提出槽式聚光镜系统有限元分析模型的建模方法，说明了建模过程和注意事项，特别是说明了聚光镜组的聚光器结构和聚光镜面等的简化原则.

2)基于MIDAS/Gen有限元分析软件对槽式聚光器建立了模态分析模型，开展了材料定义、截面定义、模型建立、网格划分、边界条件、计算程序的设置和运行研究.

3)通过模态分析得到了槽式聚光器的固有频率和振型，并与原型实测得到的固有频率和振型进行对比分析，验证了有限元模型的正确性.

需要指出的是，本文研究是对于槽式聚光镜组系统有限元分析的初步探索，还有许多问题需要进一步研究.

[1] HATHAWAY B J,LIPINSKI W,DAVIDSON J H. Heat transfer in a solar cavity receiver: design considerations[J].Numerical Heat Transfer, Part A: Applications, 2012,62(5):445-461.

[2] 刘巍,王宗超.碟式太阳能热发电系统[J].重庆工学院学报:自然科学版,2009, 23(10):99-103.

LIU W, WANG Z C. Dish-style solar thermal power generation system[J]. Journal of Chongqing Institute of Technology: Natural Science,2009, 23(10):99-103.(In Chinese)

[3] 鄂加强, 苏秀超, YANG W M，等. 碟式太阳能聚光器气动特性和最大风压分布仿真分析[J]. 湖南大学学报:自然科学版, 2015, 42(2): 8-16.

E J Q, SU X C, YANG W M,etal. Simulation analysis on the aerodynamic characteristics and maximum wind pressure distribution of dish solar concentrator[J]. Journal of Hunan University: Natural Sciences, 2015, 42(2): 8-16. (In Chinese)

[4] HSIEH J C, HUANG H J, SHEN S C. Experimental study of microrectangular groove structure covered with multi mesh layers on performance of flat plate heat pipe for LED lighting module[J]. Microelectronics Reliability,2012,52(6):1071-1079.

[5] 李明,夏朝凤.槽式聚光集热系统加热真空管的特性及应用研究[J].太阳能学报,2006,27(1):90-95.

LI M, XIA C F. Study on the characteristics and applications of evacuated tube heated by trough concentration system[J]. Acta Energiae Solaris Sinica, 2006,27(1):90-95. (In Chinese)

[6] FUDHOLI A, SOPIAN K, RUSLAN M H,etal. Review of solar dryers for agricultural and marine products[J].Renewable and Sustainable Energy Reviews,2010,14(1): 1-30.

[7] 张先勇,舒杰,吴昌宏,等.槽式太阳能热发电中的控制技术及研究进展[J].华东电力,2008,36(2):135-138.

ZHANG X Y, SHU J, WU C H,etal. Control technology and its research development for solar parabolic through power generation[J]. East China Electric Power, 2008, 36(2):135-138. (In Chinese)

[8] 韩雪冰,魏秀东,卢振武,等.太阳能热发电聚光系统的研究进展[J].中国光学, 2011, 4(3): 233-239.

HAN X B, WEI X D, LU Z W,etal. Review of concentration system in solar thermal power plant[J]. Chinese Journal of Optics, 2011, 4(3): 233-239. (In Chinese)

[9] 郑晶.槽式聚光镜结构关键技术研究[D].长沙:湖南大学土木工程学院,2014:23-37.

ZHENG J. Research on the key technology of groove type condenser structure[D]. Changsha: College of Civil Engineering, Hunan University, 2014: 23-37. (In Chinese)

[10] 邹琼,李正农,吴红华. 槽式聚光镜风压分布的风洞试验与分析研究[J]. 地震工程与工程振动,2014,34(6):227-235.

ZOU Q, LI Z N, WU H H. Wind tunnel test and analysis of the wind pressure distribution of curved mirror solar condenser[J]. Earthquake Engineering and Engineering Dynamics, 2014, 34(6):227-235. (In Chinese)

[11] ZOU Q, LI Z N, WU H H,etal. Wind pressure distribution on trough concentrator and fluctuating wind pressure characteristics[J]. Solar Energy, 2015,120:464-478.

[12] 邹琼, 李正农, 吴红华. 槽式聚光镜的脉动风压特性与极值风压分布[J].太阳能学报, 2016,37(2): 407-414.

ZOU Q, LI Z N, WU H H. Characteristics of fluctuating wind-pressure and extreme wind-pressure distribution of groove type condenser [J]. Acta Energiae Solaris Sinica, 2016,37(2): 407-414. (In Chinese)

[13] 陈伟,张军.聚光型太阳能热发电现状及在我国应用的风险分析[J].可再生能源, 2010, 28(2):148-151.

CHEN W, ZHANG J. The status of concentrating solar power and risk analysis on application in China[J]. Renewable Energy Resources, 2010, 28(2):148-151. (In Chinese)

[14] 科姆日克. Lanczos方法演变与应用[M].张伟，廖本善，译.北京：清华大学出版社, 2011：12-37.

KOMZSIK L.The Lanczos method: evolution and application[M]. Translated by ZHANG W, LIAO S B. Beijing: Tsinghua University Press, 2011:12-37. (In Chinese)

Modal Analysis of Groove Type Condenser StructureBased on MIDAS/Gen

LI Zhengnong1†, LI Lianjie2, WU Honghua1

(1.College of Civil Engineering, Hunan University, Changsha 410082,China;2. Hunan Power Engineering Company, Hengyang 421000,China)

For structure optimization of a groove type condenser,a three-dimensional finite element model of the groove type condenser was established based on MIDAS/Gen according to the groove type condenser devices located in Zhangjiagang testing ground. The method of Lanczos modes calculation was used in the model,the modal analysis was conducted under the conditions of different angles,and the structural mode characteristics of the groove type condenser were

under different working conditions. The dynamic characteristics were tested on the devices by arranging the measured points on different parts of the structure and placing sensors at the center of condensers. The dynamic signal acquisition system was used during the field measurement,the testing equipments and devices such as sensors and data acquisition instruments were used to capture the valid data of each measured point. The dynamic characteristics of groove type condenser were then acquired by processing the original data through the acquisition system. For verification of the analysis method,the finite element model was compared with the field measurements. The comparison results show that the three-dimensional finite element model can simulate the existing groove type condenser well,and it can be used in its static analysis and structure optimization analysis. In addition,the finite element modal can provide a scientific reference for further improvement on the concentrated effect of groove type condenser group and cost reduction.

groove type condenser；modal analysis；finite element method；MIDAS/Gen

TU312

A

1674-2974(2017)11-0001-10

10.16339/j.cnki.hdxbzkb.2017.11.001

2016-11-12

国家自然科学基金资助项目(51278190)，National Natural Science Foundation of China(51278190)

李正农(1962-)，男，湖北武汉人，湖南大学教授，博士生导师

†通讯联系人，E-mail：zhn88@263.net