考虑地震方向性的高耸RC烟囱结构易损性分析

周长东，田苗旺，王朋国，张许

(北京交通大学 土木建筑工程学院，北京 100044)

考虑地震方向性的高耸RC烟囱结构易损性分析

周长东†，田苗旺，王朋国，张许

(北京交通大学 土木建筑工程学院，北京 100044)

选用240 m高的某钢筋混凝土烟囱作为研究对象，通过有限元软件ABAQUS，采用复合壳单元建立了相应的非线性有限元分析模型.为考虑地震动的不确定性，根据谱相容性原则，选择了20条合理的地震动记录，进行增量动力分析.分别以材料应变和地面峰值加速度作为结构地震需求参数和地震动强度参数，通过增量动力分析将三维地震动以7种不同入射角度作用于结构并获得的结构地震响应，采用能力需求比模型的曲线拟合法计算结构的易损性.通过钢筋和混凝土的材料应变定义了4个损伤状态限值，最终得到了考虑地震方向性的高耸钢筋混凝土烟囱结构地震易损性曲线.研究结果表明，考虑地震方向性后，当PGA小于0.2 g时，该烟囱的最不利地震波输入角度大约在75°～90°左右，结构完全损伤概率大约增大了1.5%；当PGA大于0.2 g时，该烟囱的最不利地震波输入角度在45°左右，结构完全损伤概率大约增大了2.4%.

烟囱；地震响应；三维地震；增量动力分析；地震作用方向性

地震作用于结构的方向是任意的.对于有较大偏心距、平面不规则的工程结构，地震作用下容易发生弯扭耦合效应，导致不同的地震波入射角下所得到的结构响应差异较大.对于烟囱而言，由于其使用功能的要求，底部开洞往往使得烟囱不是中心对称结构.在以往的研究中一般将烟囱的开洞方向作为地震波的输入方向，忽略了地震方向性的影响.而高耸烟囱结构周期较长、高阶振型的影响不可忽略，研究地震波输入的方向对高耸烟囱结构动力响应的影响，可以得到不同方向地震作用下烟囱的结构响应，从而保证烟囱结构的抗震安全性.

在考虑多维地震作用对结构的响应时，规范[1-3]基本是根据结构的重要程度和平面布置，采用振型分解反应谱法和时程分析法，通过分别在结构的两个主轴施加地震荷载，再将结构反应进行组合的方法来考虑结构在双向地震下的最不利结构反应.Athanatopoulou等[4-5]研究了不同角度输入三维地震动作用对多层钢筋混凝土框架结构抗震性能的影响，结果表明，最不利角度下得到的结构响应比通常的地震波沿着结构对称轴输入增大了80%.Rigato[6]等人以双向地震波作用于单层建筑结构为例，研究了地震波入射角对多个工程需求参数的影响.在双向地震动作用下，当考虑不同角度的地震输入时，沿着建筑物的对称轴输入会低估该结构的峰值塑性变形.考虑地震入射角影响后结构的最大变形响应有所增大，同时对于每条地震波的最大响应可能发生在任意的地震波入射角下.张宇[7]对地震方向性的研究表明，结构的最不利入射角与地震波、结构特性有关.对于一般结构，地震最大反应一般不会发生在结构主轴方向，若只考虑结构主轴方向的地震动输入会造成一定的误差，并且当结构进入塑性状态后，相应的最不利入射角和最大结构反应一般会发生变化.Lagaros[8]研究了地震方向性对框架结构的抗震性能影响，结果表明结构响应与地震动、地震强度和地震动入射角度有关.Lu[9]等人研究了不同的地震波入射角对斜交桥的影响，结果表明水平双向正交地震输入的最不利地震输入角度分别为0°，60°和120°.Basu等[10]研究了地震波入射角对高速桥梁的影响，结果表明,在一维地震作用下结构最大地震需求为地震波入射角在30～60°之间.张如林等[11]对某沉管隧道进行了考虑不同地震动激励方向的动力时程分析，结果表明地震激励方向对管节结构的剪力和弯矩影响较大.贺拥军等[12]对某种巨型网格结构进行了不同方向地震波作用时程对比分析，研究表明立体桁架内不同位置杆件对不同方向地震波响应有所不同.

为了研究地震波输入方向性对高耸钢筋混凝土烟囱结构易损性的影响，本文以文献[13]中的钢筋混凝土烟囱为工程背景，采用有限元软件ABAQUS建立结构三维非线性模型，通过选取一系列合理地震动，考虑三维地震作用，将地震波分别以7种不同角度输入进行增量动力分析(Incremental Dynamic Analysis,IDA).分别以材料应变和地面加速度峰值(Peak Ground Acceleration,PGA)作为结构需求参数(Engineering Demand Parameter,EDP)和地震动强度参数(Intensity Measure,IM)，对应于规范划分的5个烟囱破坏等级，通过钢筋和混凝土的材料应变定义了4个损伤状态限值.结合IDA所获得的结构地震响应，最终形成钢筋混凝土烟囱结构在不同方向地震作用下的地震易损性曲线，对烟囱在不同方向地震动输入下的损伤概率进行比较分析，从概率的角度分析该高耸烟囱结构的地震波最不利入射角度，从而更加全面地评估高耸烟囱的抗震性能.

1 烟囱三维模型的建立

1.1 工程概况

某发电公司的单筒式钢筋混凝土烟囱始建于上世纪90年代，其主体结构高度为240 m，顶部出口内壁直径(不含内衬)为7.34 m，底部内壁直径(不含内衬)为22.94 m，基础为圆板形式，基础半径为18.5 m，基础厚度为4.0 m，该结构具体参数见文献[13].该烟囱位于江苏省，抗震设防烈度为7度，50年超越概率10%的设计基本地震水平加速度峰值为0.10 g，场地类型为Ⅲ类场地，设计地震分组为I组.

1.2 ABAQUS有限元模型建立

本文采用有限元程序ABAQUS，基于分层壳模型建立整个烟囱结构的三维空间有限元模型，如图1所示.采用通用的、适用性较强的有限应变壳单元S4R来模拟烟囱筒壁；取分层数为12，其中内外侧保护层取2层，内外侧纵向钢筋和环向钢筋各取1层，核心混凝土取4层，如图2所示.

图1 基于ABAQUS的烟囱三维有限元模型Fig.1 The 3D model of chimney structure based on ABAQUS

图2 筒壁分层示意图Fig.2 The diagram of concrete shell layering

采用ABAQUS提供的纵梁(Stringer)模拟各节环形悬臂，采用局部分层壳钢筋层厚度加厚方法模拟烟道口附近的加密钢筋，通过ABAQUS提供的质量单元将每节筒壁上的内衬和隔热层的重量施加于相应高度的环形悬臂上来模拟其对结构的动力响应.沿烟囱高度方向网格尺寸取为3 m，沿烟囱圆周方向网格按圆心角为7.5°划分，开口区域进行了网格加密来获得更精确的应力.

选取混凝土塑性损伤本构模型(Concrete Damaged Plasticity)来模拟混凝土材料的开裂和压碎等力学现象，此模型是一种基于塑性的连续介质损伤模型，其受拉、受压的应力-应变曲线如图3所示，该模型的滞回准则由损伤因子d和刚度恢复系数w共同决定.刚度恢复系数w分为受拉刚度恢复系数wt和受压刚度恢复系数wc，分别表示混凝土应力-应变曲线从受压区过渡到受拉区和从受拉区过渡到受压区时，弹性模量的变化程度.混凝土从拉应力变到压应力时，由于裂纹闭合，受压刚度将会恢复，而产生受压微裂纹时，由受压变为受拉时的受拉刚度将不会恢复.故wt=0及wc=1表示只有受压刚度恢复而没有受拉刚度恢复.混凝土塑性损伤本构参数见表1.

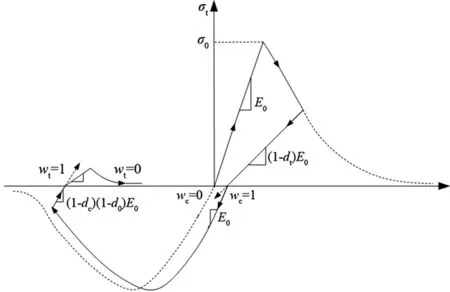
图3 混凝土单轴受力的应力-应变曲线Fig.3 Stress-strain curve of concrete under uniaxial force

膨胀角/(°)偏心率双轴与单轴极限抗压强度比不变应力比黏聚系数380.11.160.6670.0002

钢筋采用考虑包辛格效应的双折线强化本构模型，弹性阶段的弹性模量Es是钢筋强化阶段弹性模量E的100倍，卸载及在加载的弹性模量为弹性阶段的弹性模量，其钢筋本构模型如图4所示.混凝土和钢筋参数见表2.采用瑞雷阻尼来考虑结构的阻尼效应，其中钢筋的阻尼比取0.02，混凝土的阻尼比取0.05.

图4 钢筋本构模型Fig.4 The constitutive model of rebar

材料弹性模量E/Pa泊松比ν应力σ/MPa塑性应变ε钢筋2×10110.333504550.05核心混凝土3×10100.2--考虑损伤的混凝土2.5×10100.2--

1.3 模型验证

为了考虑烟囱结构外壁被碳化以及腐蚀情况，由检测报告得到，该烟囱混凝土现阶段抽样检测的强度为29.4～38.6 MPa，采用回弹法测得的平均混凝土抗压强度为33.8 MPa.混凝土碳化深度为4～12 mm，钢筋锈蚀不明显.烟囱筒身混凝土中上部内壁存在受腐蚀现象，混凝土表面受腐蚀厚度达10～25 mm.依据《回弹法检测混凝土抗压强度技术规程》[14]对测区混凝土强度换算值进行折减，平均回弹值为Rm=33.8 MPa，折减后其强度取为18.2 MPa.但将结构混凝土强度全部折减建模进行模态分析，得到的结果与实测相比误差较大，这是因为并非所有的混凝土均发生损伤，混凝土的腐蚀损伤由外及内逐渐减弱.考虑结构由于环境因素的长期损伤后，经过多次模型分析，将核心混凝土分为4层，中间两层混凝土强度取33.8 MPa，内外两层以及保护层混凝土强度取18.2 MPa，模态分析的结果与实测数据[13]较接近，详见表3.

表3 钢筋混凝土烟囱的自振特性

2 结构的地震易损性分析概述

结构的地震易损性是一种基于概率的结构抗震性能评估方法，是指在给定的地面运动参数值下，结构发生超过某个损伤程度的条件概率.通过易损性分析，可以直观地得到在不同强度地震作用下，结构的损伤达到某一程度的概率.

2.1 易损性分析流程

本文基于IDA方法[15]，得到每条地震动激励下的钢筋和混凝土的最大应变.以能力需求比模型来进行曲线拟合，直接将结构的非线性时程分析得到的地震需求与某个损伤状态相应的损伤指标相比，再将其与地震动强度绘制在对数正态坐标系下，并且进行最小二乘法的二次多项式回归求得回归系数a,b和c，根据式(1)和式(2)得到回归均值λ和方差σ，并利用式(3)计算该极限状态下的损伤超越概率[16].

λ=a(ln(PGA))2+bln(PGA)+c

(1)

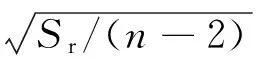
(2)

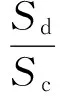
(3)

式中:a,b和c为回归统计分析得到的系数；Sr为各离散点对于回归曲线的残方差和；Sd和Sc分别为结构的需求和能力；n为离散点的个数.由不同地震强度作用下超越某一特定损伤状态的超越概率，最终得到光滑的易损性曲线[17].

2.2 损伤指标的确定

结构的损伤指标(Damage Measure,DM)是一个用来定义结构损伤状态的物理量，它本质上代表着结构的抗震能力，一般选取应变、曲率以及位移作为损伤指标.通过相关学者研究[18-19]，本文采用材料应变作为损伤指标来判断烟囱结构进入弹塑性阶段时的损伤状态.基于Python语言对ABAQUS进行编译脚本，提取整个地震分析结果文件中的混凝土和钢筋材料的最大应变值(混凝土为压应变最大值，钢筋为拉应变最大值)以及出现的相应位置.

2.3 损伤等级和极限状态

在地震易损性研究中，通常将结构在地震作用下的损伤状态划分为许多等级.《建(构)筑物地震破坏等级划分》[20]中将常用构筑物破坏等级划分为Ⅰ(基本完好)、Ⅱ(轻微破坏)、Ⅲ(中等破坏)、Ⅳ(严重破坏)、Ⅴ(毁坏)5个等级，这5个等级可以通过以下4个极限状态进行确定.

1)第1极限状态(Limit State1，LS1).基于过镇海等[21]的研究，当混凝土的应变小于等于其峰值应变εp时，混凝土的损伤程度符合Ⅰ级(基本完好)的宏观描述[20]，将εp定义为混凝土第1极限状态的压应变限值.我国现行规范中，普通混凝土的εp约为0.002.

定义第1极限状态的钢筋拉应变限值为钢筋达到初始屈服时的应变εp.本文采用的钢筋为HRB335，其εp为0.001 675.

2)第2极限状态(Limit State2，LS2).我国现行规范[1]中，混凝土极限压应变为0.003 3；印度规范[22]认为在压弯破坏情况下混凝土最外侧的极限压应变为0.003 5；美国规范[23]认为在混凝土极限受压纤维处的最大允许应变等于0.003.过镇海等[21]的研究中，当混凝土棱柱体轴压应变小于0.003 5(小于2εp，偏于保守)时，结构仅出现多条纵向裂缝，没有出现宏观斜裂缝，符合Ⅱ级(轻微破坏)的宏观描述[20]，故定义第2极限状态下混凝土压应变限值为0.003 5.

根据我国现行规范[1]给出的压弯构件平均裂缝间距计算公式，得其弯曲裂缝的平均间距约为100 mm，可将其理解为在100 mm长度的钢筋上产生1 mm的伸长量[24]，故定义第2极限状态下钢筋拉应变限值为0.01.

3)第3极限状态(Limit State3，LS3).Zahn等人[25-27]对中空圆形混凝土柱的试验表明，当内表面混凝土压应变达到0.005时，内表面混凝土开裂剥落、截面破裂.韩强等[28]基于混凝土矩形空心桥墩循环试验，得到混凝土初始剥落的应变平均值为0.005 4.混凝土压应变小于0.005，混凝土的损伤程度符合Ⅲ级(中等破坏)的宏观描述[20]，定义第3极限状态下混凝土压应变限值为0.005.

结构达到严重破坏时，混凝土开裂剥落，纵向钢筋产生更大应变.文献[29]建议混凝土桥墩达到严重破坏时，纵向钢筋的应变限值应为0.06.考虑到高耸烟囱为薄壳结构，为保守起见，取其0.5倍作为该极限状态下的钢筋应变限值，故定义第3极限状态下钢筋的拉应变限值为0.03.

4)第4极限状态(Limit State4，LS4).在混凝土的应力-应变全曲线中，当达到混凝土的峰值压应变之后，曲线逐渐下降；当压应变从0.003到0.008时，核心混凝土压碎[23]；而受箍筋约束的混凝土的极限压应变的保守估计在0.012～0.05[19].烟囱属于薄壳结构，约束箍筋对混凝土的约束效果没有对实心混凝土的效果明显，故根据《建(构)筑物地震破坏等级划分》[20]中Ⅳ(严重破坏)的宏观描述，取0.008为结构第4极限状态的混凝土压应变限值.

FEMA-356[30]建议约束混凝土受到弯曲和轴向荷载时，其纵向钢筋的压应变最大值不超过0.02，最大拉应变不超过0.05.故定义结构倒塌(即第4极限值状态)下的钢筋拉应变限值为0.05.

综上得到钢筋混凝土损伤指标限值，见表4.

表4 损伤指标限值

2.4 地震波的选取

以混凝土抗震设计规范规定的地震动设计反应谱为目标谱，从美国太平洋地震工程研究中心(PEER)数据库中选取了10条强震地震记录(表5)，按美国NEHRP规范得到的地表以下30 m范围内不考虑是否存在岩石的土层平均剪切波速νs30为150～260 m/s的场地[31]，对应于中国规范的三类场地，选取震中距为15～80 km，所选择的10条地震记录的反应谱(Responses spectra of singe record)与目标谱(The design code spectra)的对比如图5所示，图中纵坐标为谱加速度(Spectral acceleration,Sa)，3条曲线分别为平均反应谱加速度(Arithmetic MeanSa)、平均反应谱加速度加标准差(Arithmetic MeanSa+ SigmaSa)和平均反应谱加速度减标准差(Arithmetic MeanSa- SigmaSa).在PEER数据库中下载每一条地震波3个方向的加速度时程曲线，3个方向分别为水平1方向、水平2方向、竖向.在地震波输入时，本文将水平1方向的加速度时程曲线输入到结构开洞的方向，水平2方向的加速度时程曲线输入到垂直于结构开洞的方向，竖向的加速度时程曲线输入到结构垂直方向.表5中的卓越周期是将每条地震波从3个地震方向波求SRSS反应谱后得到的.

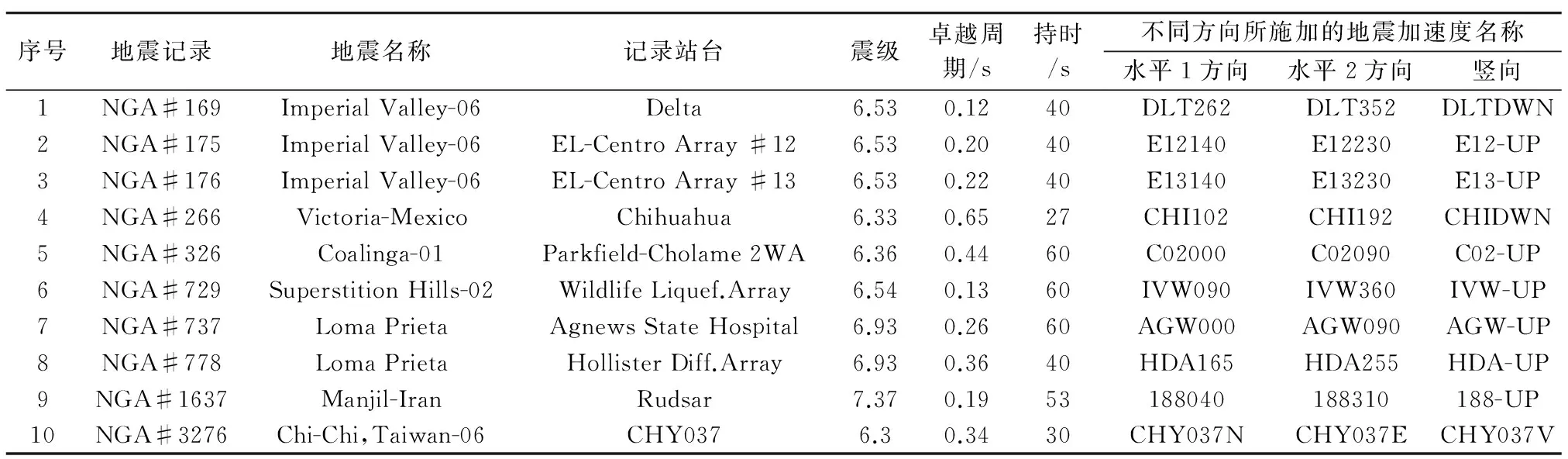
表5 用于增量动力分析的地震波

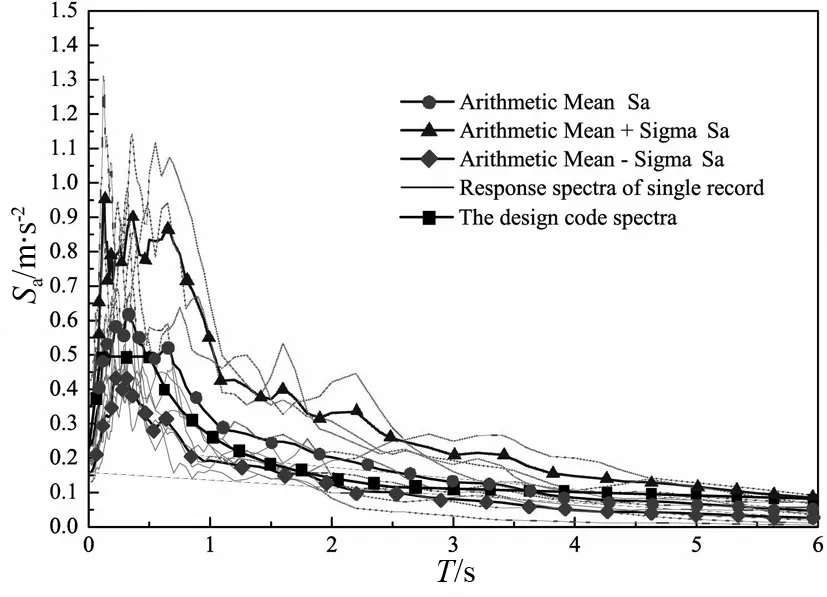
图5 所选地震记录的平均反应谱Fig.5 Mean response spectra of the selected input ground motion

3 考虑地震方向性的结构增量动力分析

对选取的10条地震波均按PGA进行调幅，调幅后的PGA分别为：0.1 g，0.2 g，…，1.0 g，调幅的级差为0.1 g，每条地震波以三维地震波输入，并根据规范建议将不同方向加速度最大值按1(水平1)∶0.85(水平2)∶0.65(竖向)，地震动水平方向1与水平方向2成90度.该高耸钢筋混凝土烟囱结构在底部X方向有2个对称的开洞，将X方向作为烟囱的薄弱方向，并将此方向作为地震波输入的主方向.考虑以不同角度输入地震波时，水平方向的地震波输入主方向与烟囱结构的X方向的夹角为θ，其大小分别为0°,15°,30°,45°,60°,75°和90°，水平方向的地震波输入示意图如图6所示.

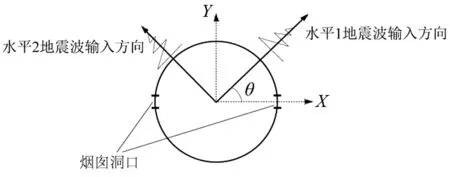
图6 地震波水平方向输入示意图Fig.6 The diagram of input way of horizontal ground motion

4 不同角度地震作用下烟囱结构的响应

本文选取表5中的EL-Centro地震波(NGA#176)为例(40 s)，具体分析不同地震波入射角作用下的结构响应.

4.1EL-Centro地震波作用下烟囱结构混凝土的响应

通过增量动力分析得到105个动力时程非线性分析结果，提取每个分析结果下混凝土最大应变εc，钢筋最大应变εs，以及最大应变出现的位置H.如图7所示，在三维地震波作用下，当地震动强度比较小(PGA=0～0.6 g)，且入射角度不同时，该烟囱结构的混凝土最大压应变基本相同；当PGA大于0.6 g之后，结构响应出现较大的离散性，其中地震波入射角分别为60°，75°和90°时结构混凝土响应比较小，地震波入射角为0°，15°，30°和45°时结构混凝土响应较大.如图8所示，在PGA=0～0.2 g时，混凝土最大应变位置出现在结构底部(0～20 m)；在PGA=0.3～0.6 g时，混凝土最大应变出现的位置有一定波动，但都为160～180 m；在PGA大于0.6 g之后，混凝土最大应变出现在结构的底部(0～20 m).

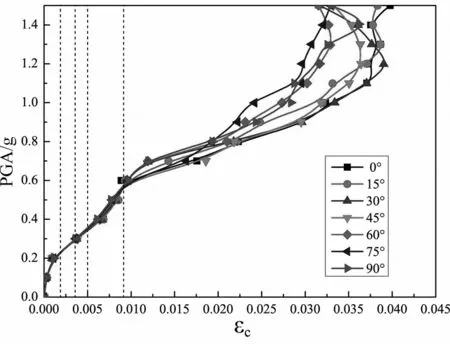
图7 混凝土最大压应变的IDA曲线Fig.7 The IDA curves of concrete maximum strain

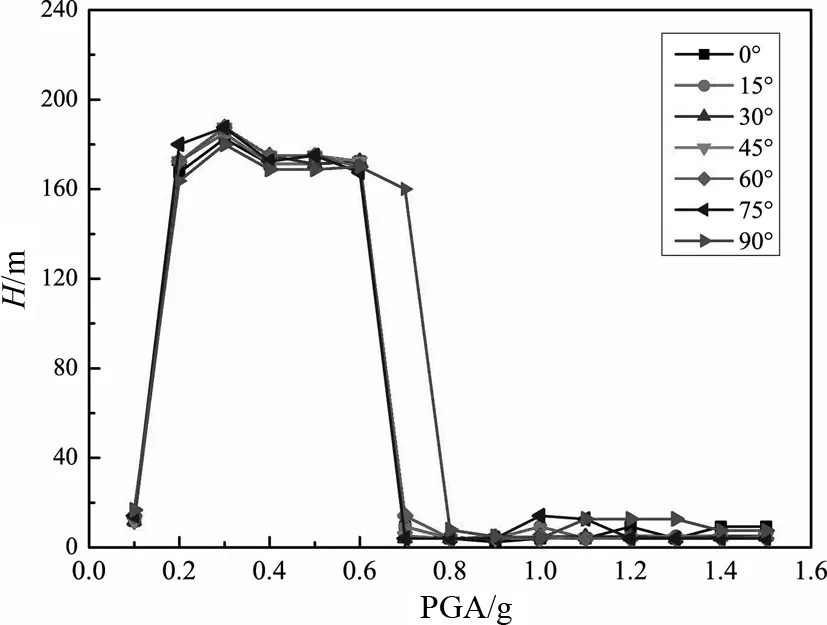
图8 混凝土最大压应变位置Fig.8 The location of concrete maximum strain

通过将不同入射角作用下所得到的混凝土最大应变与0°角的混凝土最大应变做差所得到的值与0°角作用下的混凝土最大应变作比值，得到混凝土结构响应的变化比例CR(图9).由图9可知，在PGA=0～0.15 g时，0°为最不利地震波入射方向，其他角度产生的结构混凝土响应较小；在PGA=0.15～0.3 g时，当地震入射角分别为45°，60°，75°和90°时，所得到的结构响应有所增大，地震入射角为90°所得到结构的混凝土最大应变增大幅度达到了17%，90°也是最不利地震波入射角度，若采用通常沿着结构对称轴输入地震波会低估结构的地震需求，从而对结构抗震性能的评估造成一定的误差；在PGA=0.3～0.55 g时，0°角地震作用为最不利情况；而在PGA=0.55～0.7 g时，15°，30°，45°，60°，75°和90°结构响应均比0°角地震作用大，其中地震波入射角为90°时结构混凝土最大响应增幅大约为10%.

上述分析结果表明，在同一条地震波作用下，高耸烟囱结构的最不利地震输入角度会随着地震强度的改变而发生改变.

图9 混凝土压应变变化比例Fig.9 The change rate of maximum concrete strain

4.2 EL-Centro地震波作用下烟囱结构钢筋的响应

在NGA#176地震波作用下，提取结构钢筋的最大应变(图10)，当地震动强度比较小时(PGA=0～0.4 g)，不同的入射角度对该烟囱结构钢筋应变的影响较小；PGA大于0.4 g之后，钢筋最大应变随着地震波入射角度的改变出现波动，但其中最不利情况主要为0°角地震波；当PGA大于0.8 g之后，不同地震波入射角度下所得到的钢筋峰值应变差异显著.如图11所示，当PGA=0.1～0.2 g时，不同地震波入射角度会使得结构钢筋最大应变位置发生较大变化，当地震波入射角分别为0°，15°，30°和45°时，该钢筋混凝土烟囱结构的钢筋最大应变位置出现在结构顶部230 m附近，当地震波入射角分别为60°，75°和90°时，该钢筋混凝土烟囱结构的钢筋最大应变位置出现在结构底部10 m附近；当PGA=0.3～0.6g时，钢筋最大应变出现的位置有一定波动，但均出现在150～180 m之间；当PGA大于1 g之后，最大应变出现在结构的底部(0～20 m).

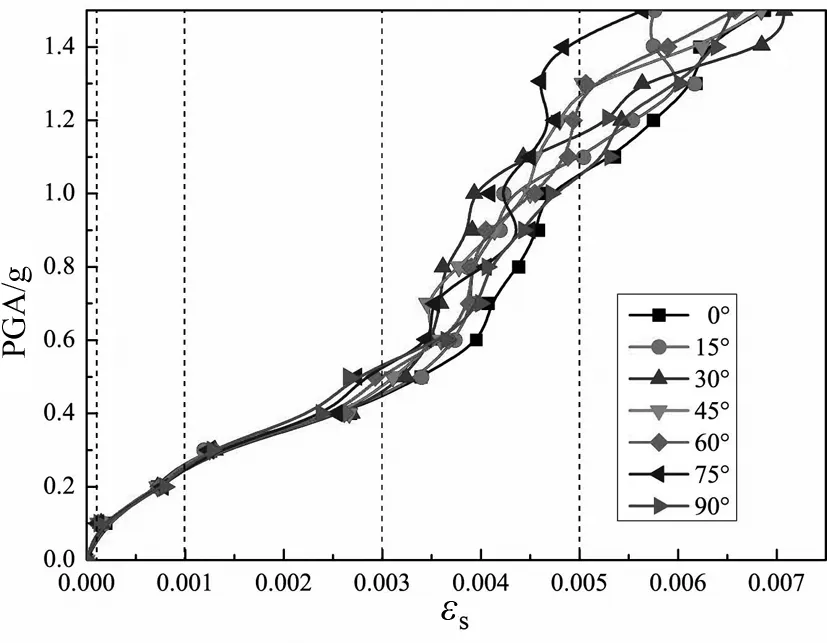
图10 钢筋最大拉应变IDA曲线Fig.10 The IDA curve of maximum steel strain

将不同入射角作用下所得到的钢筋最大应变与0°入射角情况下钢筋最大应变值之差与0°角作用下的钢筋最大应变作比值，得到钢筋结构响应的变化比例(图12)，在PGA=0～0.2 g时，地震作用的最不利方向为0°角入射方向；在PGA=0.2～0.4 g时，地震波沿着0°角入射所得到的钢筋应变最小，地震作用沿着30°输入时钢筋应变最大，钢筋应变增幅达到19%.

图11 钢筋最大拉应变位置变化Fig.11 The position of maximum steel strain

图12 钢筋拉应变变化比例Fig.12 The change rate of maximum steel strain

5 烟囱结构的地震易损性分析

5.1 烟囱结构能力需求比曲线

根据对不同地震动强度指标与结构地震响应指标之间的相关研究，以及对结构抗震分析选用地震动强度指标提供的建议，本文采用峰值地面加速度PGA作为地震动强度指标.针对调幅后的1 050条地震波动力弹塑性时程分析结果，获得各级PGA作用下结构的最大材料应变，作为该级PGA下结构的地震需求响应，得到能力需求比与地震动峰值加速度的对数IDA曲线(图13).由于工况较多，这里只列举了一条IDA拟合曲线.

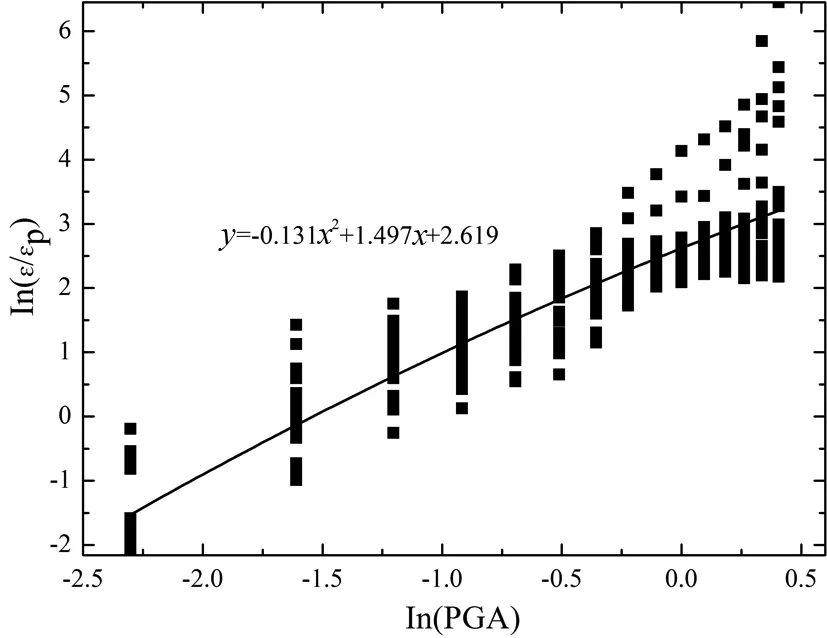
图13 地震波入射角0°下结构发生完全损伤的IDA拟合曲线Fig.13 Regression analysis of ln(demand/capacity) versus ln(PGA) when the input angle is 0°

5.2 烟囱结构地震易损性曲线

图14 不同角度下烟囱结构不同损伤状态的易损性曲线Fig.14 The vulnerability curve of RC chimney under different earthquake attack angles

采用2种方法计算该烟囱结构地震易损性曲线，第1种方法为考虑只有一种地震波入射角度作用下结构的易损性曲线，即可得到7条易损性曲线(在图14、图15中分别以0°，15°，30°，45°，60°，75°和90°表示)，这样可以得到某一地震波入射角下结构的损伤概率DP，从而通过概率大小判断结构的最不利入射角度；第2种方法为考虑地震方向性作用下结构的最不利响应，即计算结构在某一地震作用下的地震需求时，采用7种不同的角度作用下结构响应的最大值作为其地震需求，从而得到每条地震波作用下的IDA包络曲线，拟合计算得到最不利地震易损性曲线(在图14和图15中以Max表示).如图14所示，考虑单一方向地震作用下，不同地震波输入角度所得到的结构损伤概率较为接近.

通过将考虑不同地震波入射角和考虑Max最不利条件下所得到的结构损伤概率与0°入射角下所得到的结构损伤概率相减，得到不同损伤状态下，地震方向性作用对结构损伤概率的影响，如图15所示.在PGA=0～0.2 g时，结构最不利入射角度为75°～90°，相比于0°入射角情况，结构发生完全损伤概率增大量CCDP最大约1.5%；当PGA=0.25～0.6 g时，结构最不利入射角度为45°，相比于0°入射角情况下结构损伤概率最大增幅为2.4%.

考虑最不利地震波入射角下，结构在PGA=0.1～0.2 g时的轻微损伤概率增大量CSDP(图15(a))约为4.5%.中等损伤、严重损伤、完全损伤的概率增大所对应的PGA范围依次增大.当PGA=0.2～0.4 g时，考虑结构的最不利情况下(Max)的结构中等损伤增大量CMDP(图15(b))、严重损伤增大量CEDP(图15(c))、完全损伤增大量CCDP(图15(d))概率比0°入射角地震波作用情况下得到的损伤概率分别增大了约4.9%，4.5%和2.8%.因此，只考虑地震波沿着结构对称轴输入，会高估结构抗震性能，低估结构的损伤概率.

(a)轻微损伤概率变化量(b)中等损伤概率变化量(c)严重损伤概率变化量(d)完全损伤概率变化量图15 不同角度下烟囱结构不同损伤状态的概率变化量Fig.15 Thechangeofdamageprobabilityofthechimneyunderdifferentearthquakeattackangles

6 地震方向性对结构不利位置的影响

通过Python提取材料应变最大值所出现的位置进行统计分析，得到最不利位置出现在不同高度的概率PR，如图16所示，图16中0°入射角方向代表地震波沿着烟囱薄弱对称轴入射情况.

考虑地震方向性作用后，PGA=0.1 g时(图16(a))，结构底部0～30 m范围仍然是结构的一个危险区域，而结构上部危险区域由原来的160～190 m变为140～200 m，结构的最大响应更加分散；当PGA=0.2～0.4 g时(图16(b)～(d))，结构最不利位置主要集中在结构中上部(160～200 m)，局部区域100～120 m也出现了危险区域.当PGA=0.5～0.6 g时(图16(e)和图16(f))，结构的最不利位置主要集中在结构中上部(160～200 m)和结构底部(0～30 m)，随着PGA的增大，最不利位置出现中上部的概率逐渐减小，出现在结构底部的概率逐渐增大，注意到在PGA=0.6 g时，地震波入射角为15°结构的30～40 m范围内出现不利位置；当PGA=0.7～0.8 g时(图16(g)和图16(h))，结构的最不利位置主要集中在结构底部，当地震波入射角为0°和90°时，结构的最大响应位置出现在140～160 m范围内.

综上所述，不考虑地震方向性时，结构发生最大响应的位置主要集中在结构底部0～30 m，中部90～120 m，以及中上部160～200 m.考虑地震方向性后，结构最不利位置出现的范围更加分散.

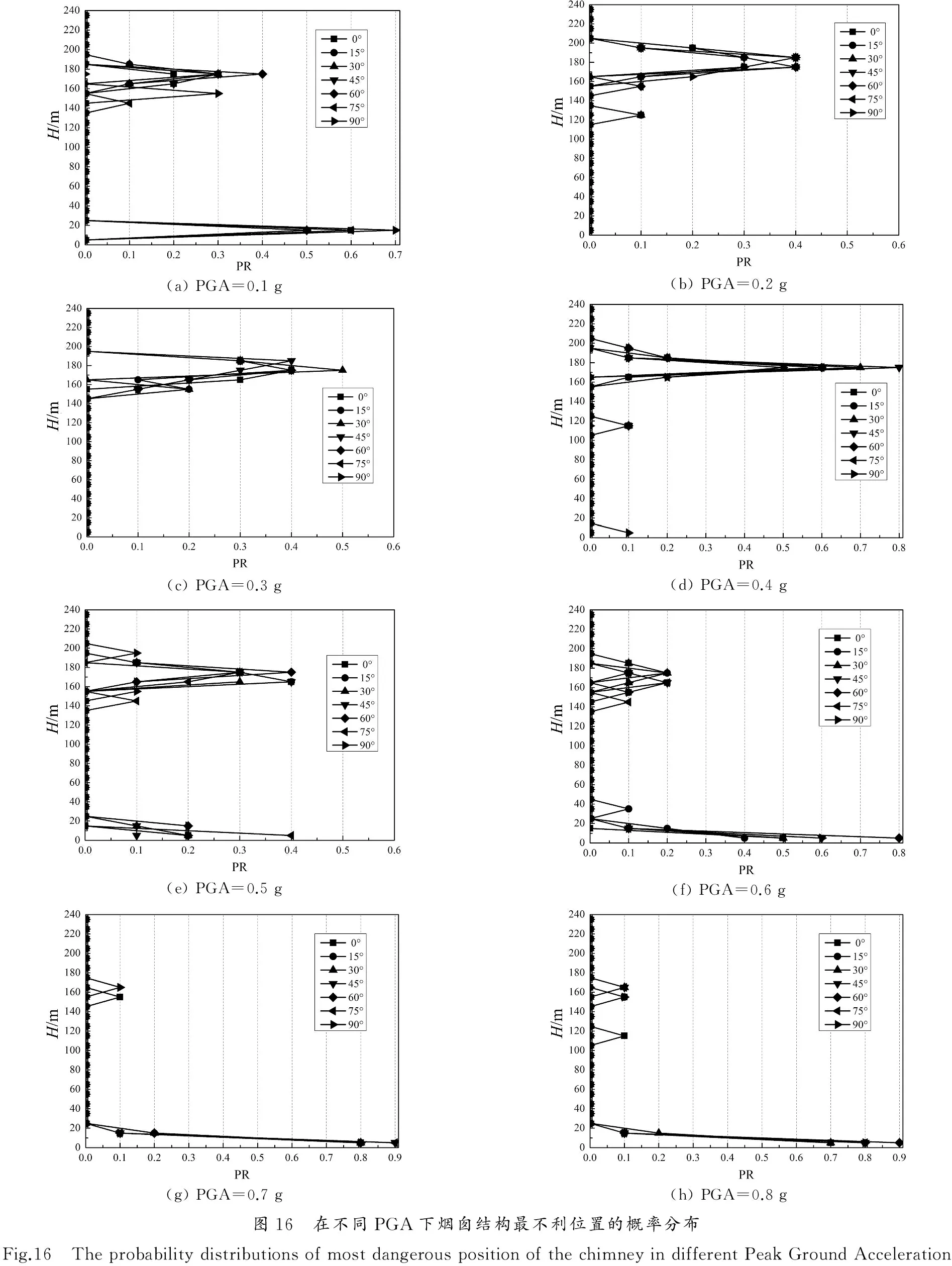
(a)PGA=0.1g(b)PGA=0.2g(c)PGA=0.3g(d)PGA=0.4g(e)PGA=0.5g(f)PGA=0.6g(g)PGA=0.7g(h)PGA=0.8g图16 在不同PGA下烟囱结构最不利位置的概率分布Fig.16 TheprobabilitydistributionsofmostdangerouspositionofthechimneyindifferentPeakGroundAcceleration

7 结 论

本文基于增量动力分析以及易损性分析，研究了地震方向性对某高耸钢筋混凝土烟囱结构响应的影响.围绕最大材料应变、结构发生不同状态损伤的概率以及结构出现最大应变的位置，分析了考虑地震方向性后该烟囱结构的抗震性能，从概率角度确定了三维地震作用下该烟囱结构的最不利地震入射角.主要研究结论如下：

1)当地震强度较大时，考虑地震方向性会对高耸烟囱结构的响应产生明显影响.

2)当PGA小于0.2 g时，最不利地震波输入角度大约在75°～90°，当PGA大于0.2 g时，最不利地震波输入角度在45°左右.建议在对烟囱结构进行地震作用分析时，除了将地震波沿着烟囱结构的薄弱对称轴输入外，还应该考虑分别以45°，75°和90°角输入地震波.

3)考虑地震方向性后，该烟囱结构发生轻微损伤的概率比0°角入射下增大4.5%、中等损伤概率增大4.9%、严重损伤概率增大4.5%、完全损伤概率增大2.8%.因此，在对开洞较大的烟囱、水塔、筒仓等结构进行地震响应分析时应考虑地震方向性的影响.

4)考虑地震方向性后，该烟囱结构的最大响应出现的位置会变得更加分散.

[1] GB 50010-2010 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社,2010:1-425.

GB 50010-2010 Code for design of concrete structures [S]. Beijing: China Building Industry Press,2010:1-425. (In Chinese)

[2] ASCE/SEI 7-05 Minimum design loads for buildings and other structures[S].Reston Virginia: American Society of Civil Engineers,2006:1-388.

[3] Eurocode 8 Design of structures for earthquake resistance[S]. Brusells: European Committee for Standardization,1998:1-215.

[4] ATHANATOPOULOU A M,TSOUREKAS A,PAPAMANOLIS G. Variation of response with incident angleunder two horizontal correlated seismic components[J]. Earthquake Resistant Structures,2005,82: 183-192.

[5] ATHANATOPOULOU A M. Critical orientation of three correlated seismic components[J]. Engineering Structures,2005,27(2): 301-312.

[6] RIGATO A B,MEDINA R A. Influence of angle of incidence on seismic demands for inelastic single-storey structures subjected to bi-directional ground motions[J]. Engineering Structures,2007,29(10): 2593-2601.

[7] 张宇. 考虑地震方向性的框架结构动力反应与性能评估[D].北京: 清华大学土木工程系,2013:1-60.

ZHANG Yu.Seismic analysis and performance evaluation of frame structures considering directionality of Bi-directional earthquakes[D]. Beijing: Civil Engineering,Tsinghua University,2013:1-60. (In Chinese)

[8] LAGAROS N D. Multicomponent incremental dynamic analy-sis considering variable incident angle[J]. Structure and Infrastructure Engineering,2010,6(1/2): 77-94.

[9] LU M Q,GUO S Q. Critical seismic response analysis of skew bridges[J]. Applied Mechanics and Materials,2014,488: 394-397.

[10] BASU S B,SHINOZUKA M. Effect of ground motion directionality on fragility characteristics of a highway bridge[J]. Advances in Civil Engineering,2011,2011: 1687-1698.

[11] 张如林,楼梦麟,袁勇.土-海底沉管隧道体系三维地震响应分析[J].湖南大学学报:自然科学版,2014,41(4): 25-32.

ZHANG Rulin,LOU Menglin,YUAN Yong. Three-dimensional seismic response analysis of soil-undersea immersed tunnel system[J]. Journal of Hunan University :Natural Sciences,2014,41(4): 25-32. (In Chinese)

[12] 贺拥军,周绪红,董石麟. 圆柱面巨型网格结构地震响应时程分析[J]. 湖南大学学报：自然科学版,2005,32(3):41-46.

HE Yongjun,ZHOU Xuhong,DONG Shilin. Research on the seismic response behavior of cylindrical latticed intersected three dimensional beam system reticulated mega structure by the time history method [J]. Journal of Hunan University:Natural Sciences,2005,32(3):41-46. (In Chinese)

[13] 曾绪朗. 高耸钢筋混凝土烟囱结构抗震性能研究[D].北京:北京交通大学土木与建筑工程学院,2014:1-99.

ZENG Xulang.Study on seismic performance of high-rise reinforced concrete chimney structure[D]. Beijing: School of Civil Engineering,Beijing Jiaotong University,2014:1-99. (In Chinese)

[14] JGJ/T 23-2011 回弹法检测混凝土抗压强度技术规程[S]. 北京:中国建筑工业出版社,2011:7-38.

JGJ/T 23-2011 Technical specification for inspecting of concrete compressive strength by rebound method[S]. Beijing: China Building Industry Press,2011:7-38. (In Chinese)

[15] VAMVATSIKOS D,CORNELL C A. Incremental dynamic analysis [J]. Earthquake Engineering & Structural Dynamics,2002,31(3): 491-514.

[16] PAN Y,AGRAWAL A K,GHOSN M.Seismic fragility of continuous steel highway bridges in New York State[J]. Journal of Bridge Engineering,2007,12(6):689-699.

[17] 周长东，陈静，曾绪朗，等.钢筋混凝土圆形空心高墩地震易损性分析[J]. 铁道工程学报，2014，31(11)： 65-71.

ZHOU Changdong,CHEN Jing,ZENG Xulang,etal. Evaluation of seismic vulnerability of reinforced concrete circular hollow high-piers [J]. Journal of Railway Engineering Society,2014,31(11): 65-71. (In Chinese)

[18] 梁智垚. 非规则高墩桥梁抗震设计理论研究[D]. 上海:同济大学土木工程学院,2007:52-133.

LIANG Zhiyao. Study on seismic design theory of irregular girder bridges with high piers [D]. Shanghai: College of Civil Engineering,Tongji University,2007:52-133. (In Chinese)

[19] 谷音，黄怡君，卓卫东. 高墩大跨连续刚构桥梁地震易损性分析[J]. 地震工程与工程振动,2011,31(2): 91-97.

GU Yin,HUANG Yijun,ZHUO Weidong. Study on seismic vulnerability of long-span continuous rigid frame bridge with high piers [J]. Journal of Earthquake Engineering and Engineering Vibration,2011,31(2):91-97. (In Chinese)

[20] GB/T 24335-2009 建(构)筑物地震破坏等级划分[S]. 北京: 标准出版社,2009:1-8.

GB/T 24335-2009 Classification of earthquake damage to buildings and special structures [S]. Beijing: Standards Press of China,2009:1-8. (In Chinese)

[21] 过镇海,时旭东. 钢筋混凝土原理和分析[M]. 北京: 清华大学出版社,2003:82-198.

GUO Zhenhai,SHI Xudong. Reinforced concrete theory and analyse [M]. Beijing: Tsinghua University Press,2003:82-198. (In Chinese)

[22] Standard I,IS-456 Plain and reinforced concrete-code of practice[S].New Delhi:Bureau of Indian Standards,2000:1-114.

[23] ACI 318-14 Building code requirements for structural concrete and commentary[S].Farmington Hills:American Concrete Institute,2014:315-325.

[24] 刘艳辉. 基于性能抗震设计理论的城市高架桥抗震性能研究[D]. 成都:西南交通大学土木工程学院,2008:18-28.

LIU Yanhui. Research on urban viaduct seismic behaviors in performance-based seismic design theory [D]. Chengdu:College of Civil Engineering,Southwest Jiaotong University,2008:18-28. (In Chinese)

[25] ZAHN F A,PARK R,PRIESTLEY M J N. Flexural strength and ductility of circular hollow reinforced concrete columns without confinement on inside face[J]. ACI Structural Journal,1990,87(2): 156-166.

[26] WHITTAKER D,PARK R,CARR A J. Experimental tests on hollow circular concrete columns for use in offshore concrete platforms[C]. Wairakei,New Zealand: Pacific Conference on Earthquake Engineering,1987,1: 213-244.

[27] HOSHIKUMA J,PRIESTLEY M J N. Flexural behavior of circular hollow columns with a single layer of reinforcement under seismic loading [R]. San Diego: Structural Systems Research Project,2000:1-79.

[28] 韩强,周雨龙,杜修力. 钢筋混凝土矩形空心桥墩抗震性能[J]. 工程力学,2015,32 (3): 28-40.

HAN Qiang,ZHUO Yulong,DU Xiuli. Seismic performance of reinforced concrete rectangular hollow bridge columns [J]. Engineering Mechanics,2015,32(3): 28-40. (In Chinese)

[29] KOWALSKY M J. Direct displacement-based design: a seismic design methodology and its application to concrete bridges[D]. San Diego: University of California,1997:1-85.

[30] FEMA-356 Prestandard and commentary for the seismic rehabilitation of buildings[S].Washington DC: American Society of Civil Engineering,Federal Emergency Management Agency,2000:1-410.

[31] 吕红山，赵凤新. 适用于中国场地分类的地震动反应谱放大系数[J]. 地震学报，2007，29 (1)：67-76.

LÜ Hongshan,ZHAO Fengxin. Site coefficients suitable to China site category[J]. Acta Seismologica Sinica,2007,29(1): 67-76. (In Chinese)

Analysis on Structural Fragility of a High-rise RC ChimneyConsidering Ground Motion Directionality

ZHOU Changdong†,TIAN Miaowang,WANG Pengguo,ZHANG Xu

(School of Civil Engineering,Beijing Jiaotong University,Beijing 100044,China)

A 240 m-height RC chimney was chosen as the research object. Composite shell element was adopted to establish the nonlinear analytical model by using the finite element software ABAQUS. In order to perform the incremental dynamic analysis considering the uncertainty of the ground motions，20 ground motion records were selected based on the matched-spectrum principle. The peak ground acceleration and maximum strain were selected as the intensity measure and engineering demand parameters，respectively. Based on the material strain of concrete and steel rebar，the limit values of four damage states were defined. The base excited by the ground motion has seven different angles during incremental dynamic analysis. Combining with the response of structure obtained by incremental dynamic analysis，the vulnerability was calculated by the curve fitting method. The seismic fragility and collapse probability curves of high-rise RC chimney structures under different ground motions were then obtained. The results show that when the PGA is smaller than 0.2 g，the critical input angle is approximately 75°～90° and the complete damage probability increases about 1.5% considering directionality of three-directional earthquake. When the PGA is bigger than 0.2 g，the critical input angle is 45° and the complete damage probability increases about 2.4%.

chimneys; seismic response; three-dimensional ground motion; incremental dynamic analysis; ground motion directionality

TU279.742

A

1674-2974(2017)11-0011-12

10.16339/j.cnki.hdxbzkb.2017.11.002

2016-10-18

国家自然科学基金资助项目(51478033,51678039),National Natural Science Foundation of China(51478033,51678039)；中央高校基本科研业务费专项资金资助项目(2016YJS103),Fundamental Research Funds for the Central Universities(2016YJS103)

周长东(1971—)，男，山东聊城人，北京交通大学教授，博士生导师

†通讯联系人，E-mail: zhouchangdong@163.com