微分求积方法解时间分数阶扩散方程

曹 焕, 张学莹, 刘 荟

(河海大学 理学院， 江苏 南京 211100)

微分求积方法解时间分数阶扩散方程

曹 焕, 张学莹*, 刘 荟

(河海大学 理学院， 江苏 南京 211100)

微分求积(DQ)法是一种基于径向基函数(RBFs)插值的无网格方法.本文选MultiQ-uadrics(MQ)函数作为径向基函数,并采用微分求积方法解决时间分数阶扩散方程。在离散过程中,采用有限差分法离散时间项,采用微分求积方法离散空间项.最后，结合数值求解的结果做出相应的误差分析.

径向基函数； MQ函数； 微分求积法； 时间分数阶扩散方程

0 引言

近年来,反常扩散现象在物理学和工程学等领域得到了广泛的关注[1,2],比如：污染物的运输、渗流、损耗以及磁等离子体等问题.与正常的扩散现象相比,反常扩散现象具有较强的远程相互作用与历史依赖性等特点,而标准的整数阶偏微分方程已经无法准确的描述这类反常扩散行为[3].随后,分

数阶导数被陆续的证实是一种可以准确的描述这类反常扩散现象的数学模型[4].所以,为了解决这些问题,引入了分数阶扩散方程.

由于分数阶偏微分方程中含有分数阶的导数,不容易求解分数阶偏微分方程的解析解,因此很多人研究其数值解法.目前,有限差分方法[5]已被证实为对分数阶扩散方程进行时间和空间上离散的一种有效方法.对于分数阶扩散方程的数值解法，也可以选择其他合适的方法对其空间上的离散,例如:边界元法[6],有限元法[7,8],傅里叶法[9],无网格径向基函数法[10-13]等.与传统的有限差分方法对空间的离散相比较，对于处理一些大规模问题，这些方法在一定程度上减少了计算量，同时又提高了计算效率.2003年，Shu C提出DQ法解整数阶的偏微分方程,且取得较理想的结果.本文将这一方法运用到解分数阶偏微分方程中，并给出误差结果分析.

1 基本理论

1.1 时间分数阶扩散方程

(1)

0lt;αlt;1,X∈Ω,t∈(0,T)

边界条件:

u(X,t)=g(X,t)，X∈∂Ω,t∈(0,T)

(2)

初始条件:

u(X,0)=u0(X),X∈Ω

(3)

式(1)～(3)中：Q(X,t),g(X,t),u0(x)是给定的函数,T是总时间,∂α/∂tα是关于时间t的分数阶导.

本文采用Caputo时间分数阶导数的定义,定义如下:

(4)

这里0lt;αlt;1.

1.2 FDM方法对时间的离散

首先把区间[0,T]分割成K个小区间,定义tk=kτ,k=0,1,…,K,这里τ=T/K为时间步长.用u(X,tk)表示函数u(X,t)在tk处的精确解.本文利用有限差分方法在t=tk+1处对时间分数阶导数进行离散,有

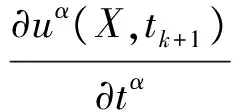
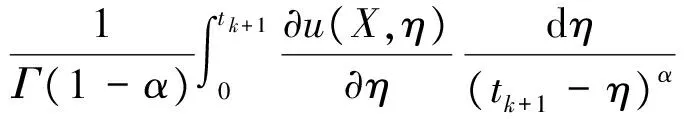
(5)

式(5)中：

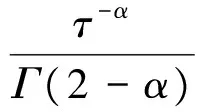
根据式(5),对方程式(1)进行时间离散,得到

Δuk+1+Qk+1=

(6)

1.3 微分求积方法对空间的离散

设f(x)是光滑函数,其中x=(x1,x2,…,xn)T.已知它在节点xi及其支撑域内各支撑点xj,j=1,2,…,n上的函数值,则f(x)关于xk的m阶导数可以表示为

(7)

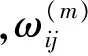
(8)

可将其写成矩阵形式是

(9)

由文献[14]可知式(9)中的矩阵是条件正定的,故系数矩阵是可逆的,从而可求得系数.再将其代入式(7),就可以求出函数f(x)关于xk的m阶导数的近似值.

由上述过程,本文采用DQ方法对方程式(6)进行空间离散,可知

(10)

再将式(10)代入式(6)得到对空间的离散,并对其整理可得

(11)

2 数值算例

本文考虑在规则区域Ω=[0,0.5]×[0,0.5]内,检验时间分数阶扩散方程的有效性和准确性.数值的准确性由均方根误差(RMSE),最大绝对误差(MAE)和最大相对误差(RAE)计算.其误差定义如下：

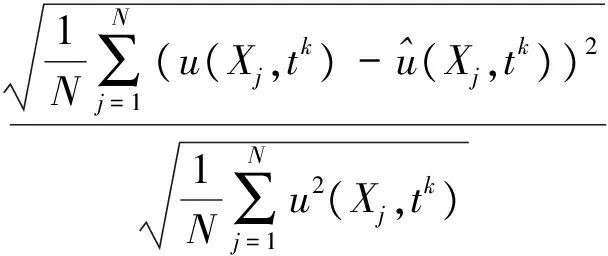
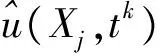
算例

0lt;αlt;1,X∈Ω,t∈T

边界条件:

u(X,t)=t2ex+y,

X∈∂Ω,t∈(0,T)

初始条件:

u(X,0)=0,X∈Ω.

α=0.9,Ω=[0,0.5]2，

Q(X,t)=(2t2-α/Γ(3-α)-2t2)ex+y.

该方程的精确解为

u(X,t)=t2ex+y,x∈Ω,t∈(0,T).

图1为选取网格点N=961,分数阶导数α=0.9,时间步长dt=0.1,参数c=0.05时的绝对误差和相对误差图.

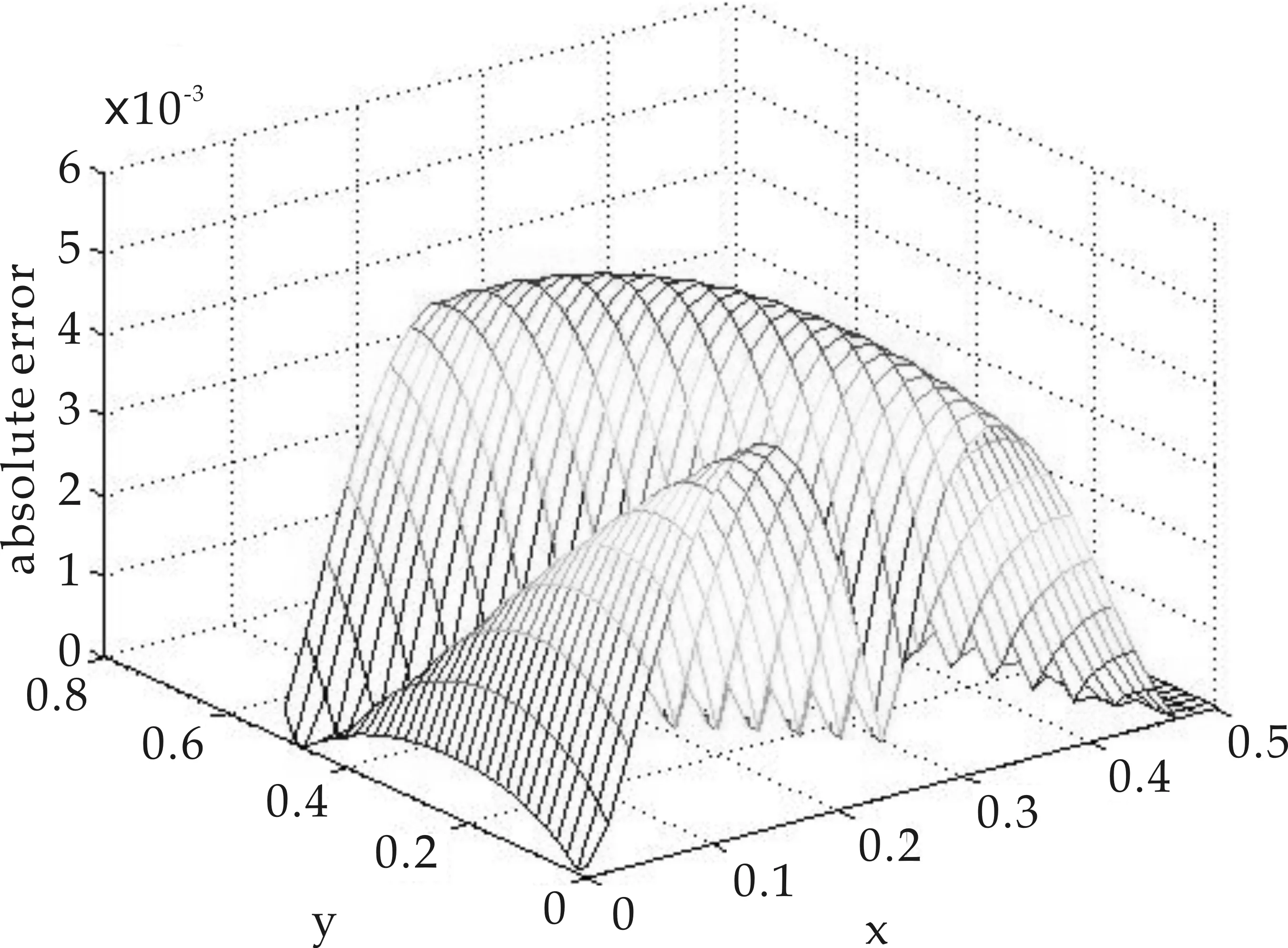
(a) N=961,α=0.9,dt=0.1,c=0.5时绝对误差图

(b) N=961,α=0.9,dt=0.1,c=0.5时相对误差分布图

图2为选取分数阶导数α=0.9,参数c=0.02时,随着插值点个数增加,不同时间步长下的均方差对比图;图3为选取分数阶导数α=0.9,时间步长t=0.1时,随着插值点个数增加,不同参数下的均方差对比图.

图2 不同时间步长下的均方根误差比较

图3 不同参数c下的均方根误差比较

从图2和图3可以看出,参数c和时间步长的选取对数值结果有较大的影响,当选取较大的时间步长时,精度有明显的提高,当插值点个数为256时,精度达到最高,当插值点个数的增加,精度变化幅度逐渐减小,最终趋于稳定,但如果点再继续增加,就可能会出现病态;当选取较小的参数c时,随着插值点个数的增加,精度开始有明显的提高,但当插值点个数再增加时,精度变化幅度逐渐减小,最终趋于稳定.因此,选取适当的时间步长和参数c是提高数值结果精度的有效方法.

表1为选取时间步长t=0.1,参数c=0.02时,不同分数阶导数下的绝对误差和相对误差的结果比较.

表1 t=0.1，c=0.02时不同α下的绝对误差和相对误差比较

从表1可以看出,当取时间步长t=0.1,参数c=0.02,分数阶的导数越接近1时,随着插值点个数的增加,误差越来越精确.

3 结论

本文在结合有限差分方法的基础上，应用微分求积方法对规则区域上的时间分数阶扩散方程进行数值求解.根据Caputo分数阶导数的积分定义,利用有限差分方法对时间导数进行离散,利用微分求积方法对空间导数进行离散,并通过数值算例得出数值结果.

数值结果表明,微分求积方法是解决时间分数阶扩散方程比较可行的方法.在解决问题的过程中，选取了MQ函数作为径向基函数,从图3可以看出参数c的选择对数值结果具有很大的影响,当选取适当参数c时,数值结果的精度更高.同时，还可得出时间步长和插值点个数也对其具有一定影响.

后续，还可进一步讨论在不规则区域上此方法的可行性以及怎样选取参数c可使数值结果达到更好的精度.

[1] R Gorenflo,F Mainardi,D Noretti,et al.Discrete random walk models for space time fractional diffusion[J].Chenmical Physics,2007,284(1-2):521-541.

[2] L Baowen,W Jiao.Anomalous heat conduction and anomalous diffusion in onedimensional systems[J].Physical Review Letters,2003,91(4):318-322.

[3] Zhang X Y,Zhu H Q,Kuo L H.A comparison study of the LMAPS method and the LDQ method for time-dependent problems[J].Engineering Analysis with Boundary Elements,2013,37:1 408-1 415.

[4] F Liu,V Anh,I Turner,et al.Time fractional advection dispersion equation[J].Journal of Applied Mathematics and Computing,2003,13:233-245.

[5] H Wang,K Wang,T Sircar.A direct O (Nlog2N) finite difference method for fractional diffusion equations[J].Journal of Computational Physics,2010,229(299):8 095-8 104.

[6] Katsikadelis J T.The BEM for numerical solution of partial fractional differential equations[J].Computers amp; Mathematics with Applications,2011,62(3):891-901.

[7] Li C,Zhao Z, Chen Y. Numerical approximation of nonlinear fractional differential equations with subdiffusion and superdiffusion[J].Computers amp; Mathematics with Applications,2011,62(3):855-875.

[8] Jiang Y,Ma J.High-order finite element methods for time-fractional partial differential equations[J].Journal of Computational amp; Applied Mathematics,2011,235(11):3 285-3 290.

[9] Chen C M,Liu F,Turner I,et al.A Fourier method for the fractional diffusion equation describing sub-diffusion[J].Journal of Computational Physics,2007,227(2):886-897.

[10] Chen W,Ye L,Sun H.Fractional diffusion equations by the Kansa method[J].Computers amp; Mathematics with Applications,2010,59(5):1 614-1 620.

[11] Liu Q,Gu Y,Zhang P,et al.An implicit RBF meshless approach for time fractional diffusion equations[J].Computational Mechanics,2011,48(1):1-12.

[12] Fu Z J,Wen Chen,Leevan Ling,el al.Method of approximate particular solutions for constantand variable-order fractional diffusion modes[J].Engineering Analysis with Boundary Elements,2015,57:37-46.

[13] Chen W,Fu Z J.Recent advances on radial basis function collocation methods[M].Berlin:Springer Berlin Heidelberg,2014.

[14] Micchelli C A.Interolation of scattered deta:Distance matrices and conditionally positive definite functions[J].Constr Approx,1986(2):11-22.

【责任编辑：蒋亚儒】

Thedifferentialquadraturemethodsolutionsforthetime-fractionaldiffusionequation

CAO Huan, ZHANG Xue-ying*, LIU Hui

(School of Science, Hohai University, Nanjing 211100, China)

The differential quadrature method is an alternative radial basis functions (RBFs) meshless method.This article selects MQ function as the radial basis function,and applys the differential quadrature method to solve the time fractional diffusion equation.In the discretization formulation,a finite difference scheme and the DQ are used repectively to discretize time fractional derivative and spatial derivative terms.Finally we make the error analysis with the results of the numerical investigation example.

RBFs; MQ function; DQ method; time fractional diffusion function

2017-08-27

教育部留学回国人员科研启动基金项目(20145003412)； 江苏省自然科学基金项目(BK20160853)

曹 焕(1992-)，女，山东菏泽人，在读硕士研究生，研究方向：计算数学

张学莹(1973-)，男，山东郯城人，副教授，硕士生导师，研究方向：计算数学， zhangxy@hhu.edu.cn

2096-398X(2017)06-0179-04

O241.82

A