纤锌矿结构AlN、GaN及ZnO自发极化的第一性原理研究

牛海波， 竹有章， 李冠强

(1.西安交通大学城市学院 物理教学部， 陕西 西安 710018； 2.陕西科技大学 文理学院， 陕西 西安 710021)

纤锌矿结构AlN、GaN及ZnO自发极化的第一性原理研究

牛海波1， 竹有章1， 李冠强2

(1.西安交通大学城市学院 物理教学部， 陕西 西安 710018； 2.陕西科技大学 文理学院， 陕西 西安 710021)

根据现代极化理论，分别利用Berry phase方法和最大局域化Wannier函数方法系统计算了纤锌矿结构AlN、GaN及ZnO中的自发极化，并从电子项和离子项引起的极化变化具体分析了自发极化的起源.研究表明AlN自发极化中电子项的贡献占据主导地位，而GaN及ZnO自发极化中以离子项的贡献为主.研究发现其他文献计算自发极化时，由于计算模型和参考模型使用相同的体积，导致计算结果偏小.利用Wannier中心，从结构中最小重复单元的电偶极矩出发对原有计算公式进行了修正，使得自发极化的计算结果更趋合理.研究发现在特定建模条件下，可以不用计算参照模型中的极化，利用Wannier中心确定纤锌矿结构中正负电荷的重心，通过经典的静电学理论直接计算出自发极化，直观解释了自发极化的形成.

纤锌矿结构； 自发极化； Wannier中心； 第一性原理

0 引言

AlN、GaN及ZnO作为典型的第三代半导体材料，具有直接带隙且带隙宽度大的显著优点[1,2]，因而呈现出优异的发光特性，在蓝光、深紫外发光器件及光电探测器件等领域具有重要的应用价值.如随着高质量P型GaN(禁带宽度3.4 eV)制造工艺的突破[3]，GaN基蓝绿光发光二极管已经研制成功并商品化，占据了发光二极管市场的绝大多数份额.2006年，Taniyasu等[4]成功制作出直接基于AlN的发射波长为210 nm的深紫外发光二极管,成为迄今为止在氮化物半导体领域获得的最短发射波长.通过将AlN、GaN及InN组成三元或四元合金，发光谱更是覆盖了从红外到紫外的整个区域[5].这些优点使得AlN、GaN及ZnO成为目前最有发展前景的半导体发光材料，吸引了众多研究者的广泛关注，并得到迅猛发展.

Ⅲ族氮化物及ZnO等宽禁带半导体材料的突出特征是晶体结构中存在较大的自发极化.由于这些晶体自然状态下的稳定结构多为六方对称的纤锌矿结构，这种结构的特点是每一个原子与其最近邻的四个原子所成的化学键中，沿[0001]方向的键比其他三个稍长，使得原胞中正负电荷中心不重合，产生电偶极矩，形成了内建电场，即存在自发极化.极化效应对材料的光电性质存在重要影响.

近年来受到广泛关注的AlGaN/GaN异质结材料，正是因为结构中内生的极化场，导致即使在非故意掺杂情况下也存在超高密度的二维电子气(载流子浓度高达1013/cm2)[6,7]，非常适合制作一些特殊性能的传感器件.另一方面，极化场对掺杂元素的浓度及掺杂位置也有较大的影响[8,9]，如在异质结中极化场使得氢元素向表面运动；强极化场还会造成能带弯曲[10]，阻碍电子和空穴对的复合，降低器件的发光效率[11].在太阳能电池中，极化场降低了吸收层的总电场，减小了光生载流子的收集效果，从而降低了太阳能电池的性能[12].极化场是研究宽禁带半导体性质时不可回避的本质问题，研究极化场性质，并对其加以调控，避短扬长，将加快宽禁带半导体的发展与应用.

本文根据现代极化理论，通过构建参照模型和计算模型，分别利用Berry phase及最大局域化Wannier函数(MLWF)方法[13-15]对纤锌矿AlN、 GaN及ZnO的自发极化进行了系统的计算，研究了影响晶体自发极化大小的各种因素，同时对其他文献报道的结果进行了分析，指出文献中所用方法的不足并进行了公式修正，使得计算结果更加合理.此外根据计算得到的Wannier 中心，从三种晶体结构的最小重复单元中电荷的重心分布出发，重新计算了三种结构的自发极化，对自发极化的形成给出了更直观的解释.

1 计算方法及模型

根据现代极化理论，为了计算纤锌矿结构中的自发极化值，首先需要建立一种正负电荷中心重合的对称结构作为初始结构(也称参照结构)，这样才能保证参照结构中的自发极化为0.纤锌矿结构与该参照结构的极化值之差才是纤锌矿结构中的自发极化.立方对称的闪锌矿结构满足上述建模要求，一般被用作参照模型.这种思想可以表述为，

ΔP=Pw-Pz

(1)

式(1)中：ΔP为纤锌矿结构中的自发极化，Pw、Pz分别为纤锌矿和闪锌矿形式上的极化值，该值可用式(2)表示成离子项Pion和电子项Pel之和，

P=Pion+Pel

(2)

由于介质中的离子分布非常局域，因此离子项的贡献可以用经典的点电荷模型进行计算，即

(3)

对Pel的计算是现代极化理论的精华，Berry phase方法给出的结果为[15]，

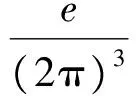
(4)

n代表了电子占据的能带，利用最大局域化Wannier函数方法，Pel可表示为[13]，

(5)

式(5)中：ωj和qj为第j个Wannier中心的位置和所带的电荷数，V为晶胞体积.根据现代极化理论，在系统绝热缓慢地从初始状态到末了状态的演变过程中，由于每个状态的极化值在计算时量子几何相位(贝利相)是对2π取模计算出来的，导致会产生极化量子数eR/V[15]，其中R为晶格参数，V为单胞体积.如果每个状态的极化量子数不同，将对极化值的改变量ΔP产生干扰.而在实际计算时如本文所研究的自发极化，由于|ΔP|=|eR/V|，即演变过程中每个状态具有相同的量子数，因此ΔP可避开极化量子数的干扰，使得自发极化具有确定值.

由于纤锌矿结构沿[0001]方向按照ABAB顺序堆垛而成，而闪锌矿结构沿[111]方向按照ABCABC顺序堆垛，因此为了不仅保证两种结构中原子数目一致，而且要求计算量最小，构建了1×1×3的纤锌矿型晶胞及1×1×2的闪锌矿型晶胞，每种模型共有12个原子.以AlN为例，分别包含了6个N原子及6个Al原子.建模时首先构建闪锌矿参照模型，然后按照ABAB的堆垛顺序将参照模型中的N、Al原子进行移动，初步构建成为纤锌矿模型.最后对闪锌矿和纤锌矿模型进行充分的结构优化(晶格参数、原子位置都允许变化).所建模型如图1所示.

(a) 闪锌矿结构 (b) 纤锌矿结构

与其他文献计算中所用到的大的超胞模型相比，本文所建模型原子数目少，因此计算量减小，此外本文对闪锌矿参照模型和纤锌矿模型都进行了完全的结构优化，使得两种模型各自呈现出典型的闪锌矿及纤锌矿结构特点，而不必保持相同的体积，这是提高计算合理性及准确性的重要保证.

采用第一性原理计算软件Quantum-Espresso[16]进行结构优化、静态自洽及非自洽计算，MLWF由Wannier90软件包进行计算[17,18].利用广义梯度近似(GGA)的PBE来处理电子之间的交换关联能，选择的赝势为Vanderbilt超软赝势.平面波截断能为40 Ry，选取Monkorst-Park特殊K点对全布里渊区求和.ZnO、GaN自发极化计算中Zn、Ga的3d态电子也作为价电子，相应的利用Wannier90计算MLWF时也包含了Zn、Ga的3d能带.利用Berry phase方法计算[0001]方向上的极化时，该方向上需要密集K点.由于过密的K点并不能带来更高的准确性，反而会使计算量大幅增加，本文采用9×9×7对K点进行了加密，计算中总能变化收敛的标准为1.0×10-6eV，原子间相互作用力的收敛标准为0.05 eV/nm.

2 结果与讨论

极化性质对结构的晶格参数非常敏感，因此在计算自发极化前首先对AlN、GaN、ZnO的原胞进行了仔细的结构驰豫，然后再对以原胞为基础构建的闪锌矿及纤锌矿模型进行优化，得到的三种晶体原胞的晶格参数如表1所示.其中c/a为晶格参数c与垂直方向的晶格参数a的比值，参数u为纤锌矿结构中平行于[0001]方向的键长与晶格参数c的比值，反映了[0001]方向原子层的间距.三种原胞的晶格参数实验值由X射线衍射测量得到[1,2]，图2给出了优化后的AlN闪锌矿及纤锌矿结构的键角.

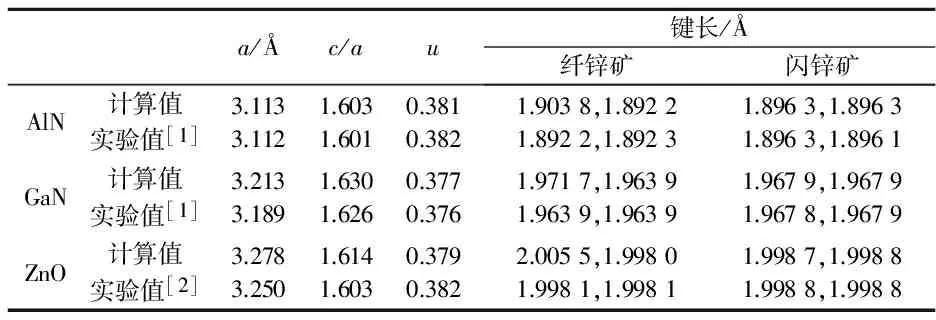
表1 纤锌矿AlN、GaN及ZnO原胞晶格参数及两种结构键长

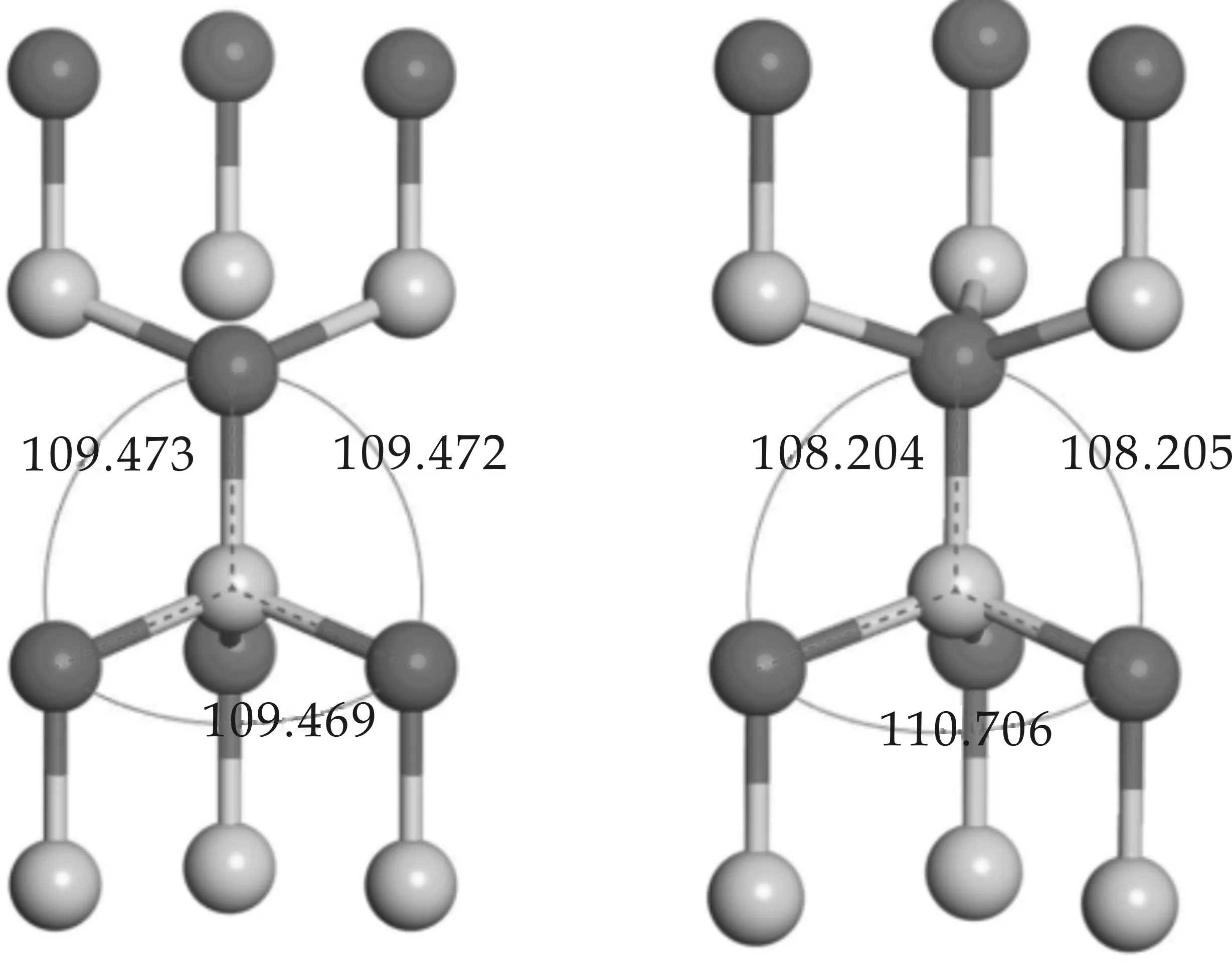
(a) 闪锌矿 (b) 钎锌矿

从表1可以看出，计算得到的纤锌矿结构原胞的晶格参数与实验值非常接近，即使在计算值与实验值相差最大的ZnO中，相对变化也只有0.89%.三种晶体的晶格参数计算值普遍稍高于实验值，这与第一性原理计算中交换关联能使用GGA近似有关.GGA近似比较适合电子密度非均匀的体系，一般情况下采用GGA近似计算得到的晶格参数均会轻微增加，这并不影响结构的对比分析.观察两种原胞中的键长，在纤锌矿结构中，垂直于[0001]方向的三个键长相等，且均小于[0001]方向上的键长，其键角为108.20 °、110.71 °，呈现出典型的纤锌矿结构特点；在闪锌矿参照结构中，四个键长一致，键角(如图2(a)所示)均为正四面体的标准键角109.47 °，符合闪锌矿的正四面体结构特征，说明了结构优化的合理性以及所建模型的准确，也保证了参照结构不存在自发极化.

2.1 利用Berry phase方法计算自发极化

首先分别对建立的闪锌矿参照结构和纤锌矿结构进行静态自洽计算，然后设置[0001]方向为极化方向进行非静态计算，可得到两种结构下的贝利相及极化值.需要注意的是，根据现代极化理论，晶体在某一状态时的极化值具有多值性，此时所求得的只是形式上的极化值，并不是该结构中的自发极化，它也没有确切的物理意义.只有纤锌矿结构与闪锌矿结构中形式上极化的差值才是纤锌矿结构的自发极化.表2中列出了AlN、GaN及ZnO 闪锌矿及纤锌矿结构中的贝利相(离子项及电子项分别列出)、对应的形式上的极化值P及纤锌矿结构中的自发极化ΔP，并与其它文献进行了对比.三种晶体中自发极化均为负值，说明它们的极化方向与[0001]方向相反.表2中贝利相φ与极化值P之间的关系为，

(6)

式(6)中：V为超胞的体积，R为超胞[0001]方向上的晶格矢量，q为电荷电量.由表2可以发现，AlN、GaN的自发极化计算值与其他文献的结果非常接近，Laehnemann等[21]利用实验测得纤锌矿GaN的自发极化为-0.022±0.007 C/m2，也与本文的计算结果符合较好，说明了所用计算模型及Berry phase方法的正确性.ZnO的计算值接近文献[19]的报道而与文献[20]差别较大，主要是因为计算中使用的交换关联能及晶格参数与文献中不同所导致，特别是参数u值不同，因为自发极化对u值更敏感.我们利用文献[20]给出的u值代替表1中ZnO的u值重新进行了计算，最后得出ZnO 的自发极化值为-0.036 C/m2，接近文献[20]的结果.

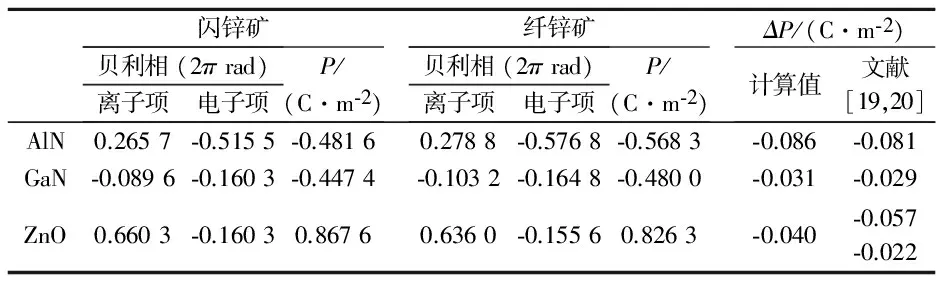
表2 AlN、GaN及ZnO的贝利相及自发极化

注意到计算出来的AlN、 GaN的自发极化值(取极化的绝对值)均稍大于文献[19]报道的结果，我们认为这是由于文献[19]中没有考虑到闪锌矿参照结构及纤锌矿两种超胞具有不同的体积，而是统一使用了纤锌矿超胞的体积所导致的.具体来说，如图1所示，两种模型尽管原子数目保持一致，但是由于结构对称性的要求，他们不可能保持相同的晶格参数与体积.而极化强度是用单位体积中的偶极矩来表征的，如果直接用计算出的两种结构的极化强度做差来计算自发极化，就表示纤锌矿和闪锌矿模型具有相同的体积，这正是引起误差的原因.准确的做法是应该用两种结构中的偶极矩做差再除以对应的纤锌矿模型的体积，这是很多之前的报道中所忽略的.进一步分析表3列出的两种结构的超胞体积，可以看到两种超胞的体积相差很小，AlN的相对体积变化在0.28%以内，但是这种微小的体积差异却是由超胞的晶格参数c变化较明显引起的，分析表3中给出的晶格参数的相对变化，AlN达到了1.3%， GaN达到了0.25%，这已经足以影响到最终的自发极化.而且可以看到正是因为AlN晶格参数的c相对变化明显大于GaN，导致了本文所计算的AlN自发极化数据与文献报道结果差异更显著.

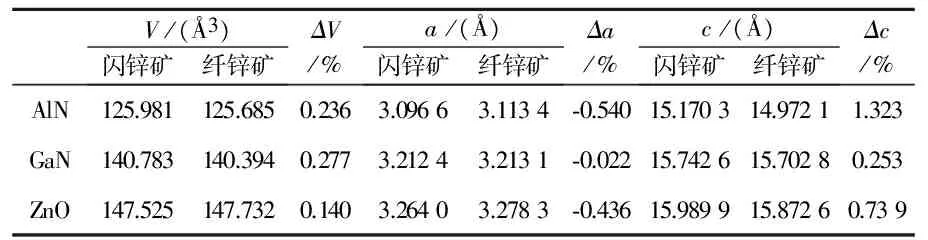
表3 AlN、GaN及ZnO闪锌矿与纤锌矿结构晶格参数、超胞体积的变化

对于上述计算得到的自发极化大于文献报道的情况，也可以通过压电极化进行定量的解释，当晶体受到外应力引起结构变形时，[0001]晶向上极化的变化为[19]，

δP=2e31ε1+e33ε3

(7)

式(7)中：ε1=(a-a0)/a0为晶体a轴受到的应力，ε3=(c-c0)/c0为晶体c轴受到的应力，e31,e33为压电系数.现在以AlN为例来进行说明，令闪锌矿结构参数使用两组数据，一组为其他文献直接使用的纤锌矿数据(记为状态1)，一组为本章所优化过的闪锌矿结构数据(记为状态2)，由表3可以看到，AlN闪锌矿结构的晶格参数a小于纤锌矿的晶格参数a0，而参数c明显大于纤锌矿结构中的c0参数，因此当闪锌矿结构从状态1变化到状态2时，ε1lt;0，ε3gt;0，而e33gt;0，e31lt;0，因此δP=P2-P1gt;0，由于P1、P2均为负值，因此|P2|lt;|P1|，再利用纤锌矿结构中的极化值与闪锌矿中的极化值做差求自发极化时，使用状态1的数据明显会使最后的自发极化值减小.

表4 结构从闪锌矿变化到纤锌矿

2.2 利用MLWF方法分析自发极化

上节利用Berry phase方法计算了晶体的自发极化，Vanderbilt等也提出了最大局域化Wannier函数方法来计算极化，通过引进局域标准求得最局域的Wannier函数，解决了Wannier函数长期以来存在不唯一性的缺点，使得MLWF方法在诸多方面得到了迅速运用.在MLWF方法中，电荷可以形象地认为局域在Wannier函数空间分布的几何中心上，该几何中心即为Wannier中心，如此一来，可将Wannier中心看做点电荷，从而整个晶体就可以分为带正电的离子和带负电的Wannier中心，晶体自发极化可用下式来计算.

(8)

式(8)中：ωj和qj为第j个Wannier中心的位置和所带的电荷数；ri和qi分别为第i个离子的位置与电荷量，V为晶胞体积.对于AlN晶体，可以认为是由+3价的Al离子、+5价的N离子以及-2价的Wannier中心组成.在计算纤锌矿GaN、ZnO中的自发极化时，由于将Ga、Zn原子的3d态电子也作为价电子，因此最后计算时需要将GaN晶体分为+13价的Ga离子、+5价的N离子及-2价的Wannier中心，ZnO晶体则分成+12价的Zn离子、+6价的O离子及-2价的Wannier中心.在构造Wannier函数时，初始空间分布选择sp3杂化轨道与d轨道，Wannier初始中心则选择N、O位置及Ga、Zn位置.图3给出了计算得到的AlN及ZnO的Wannier中心分布，可以看到ZnO中一部分Wannier中心几乎与Zn原子位置重合，这是从3d态能带得到的Wannier中心，反映了3d态电子的强局域性，其空间延展函数值也只有0.26 Å2.事实上在计算中我们发现，由于d电子局域在Ga、 Zn原子位置，导致它对GaN、ZnO的自发极化贡献很弱，在GaN中，d电子对自发极化的贡献仅占1%，在ZnO中，d电子对自发极化的贡献也仅有0.81%，因此主要的贡献来自于最外层的价电子.

(a) 纤锌矿AIN Wannier中心及Wannier函数空间分布

(b) 纤锌矿ZnO Wannier中心及Wannier函数空间分布

根据Wannier中心位置计算出闪锌矿及纤锌矿结构中的形式上的极化值，二者之差即为纤锌矿AlN的自发极化.为了进行比较，分别计算了纤锌矿结构AlN[0001]晶向，以及与它垂直的两个晶向上的自发极化以及离子部分ΔPion和电子部分ΔPel对极化的贡献，结果如表5所示.同时也将Berry phase方法计算得到的三种晶体的自发极化也列于表中进行对比.

式(8)是诸多文献中所使用的，在分析晶体保持体积不变时的极化性质时，它是完全成立的，但是我们发现在计算诸如本文所涉及的自发极化时，直接利用该式会使计算结果明显偏离公认值，如在AlN自发极化计算中，直接使用式(8)，最后的结果为-0.033 C/m2，远小于利用Berry phase方法得到的结果-0.086 C/m2，造成这一差异的原因在于闪锌矿参照结构与纤锌矿结构超胞的体积并不一致，晶格常数如c参数也不相同，这种不一致使得直接利用式(8)会带来明显的差异.在其他文献中，计算自发极化时由于闪锌矿与纤锌矿超胞都采用同一个体积，因此不存在这个情况或者说忽略了，但是两种超胞采用同一个体积计算自发极化是不合适的，因为如此构建的闪锌矿超胞并不是完全的正面体结构，导致参照结构自发极化不为零.那么为什么晶格参数不一致会导致这样大的差异，我们认为具体还在于对利用MLWF计算电偶极矩的内涵没有理解透彻，事实上，计算闪锌矿及纤锌矿超胞中的电偶极矩应该从结构中的最小重复单元如N-Al对中的偶极矩入手进行分析.图4以纤锌矿AlN为例给出了晶体中最小重复单元中的偶极矩示意图.

表5 AlN、GaN及ZnO三个晶向上的自发极化

图4 纤锌矿AlN结构最小重复单元中 的偶极矩(黑色箭头)示意图

现在以图4方框所示的最小重复单元即N-Al对的偶极矩为例进行分析，WF表示Wannier中心.MLWF方法将AlN晶体看作由-2价的Wannier中心、+5价的N离子以及+3价的Al离子组成的点电荷集合.为了计算电偶极矩，可以进一步将N、 Al离子各分成带电量相同的四等份，即将+5价的N离子看作由4个带电量分别为+1.25的离子组成，将+3价的Al离子看作由4个带电量分别为+0.75的离子组成，而每个Wannier中心则相应看作由带电量为-1.25及-0.75的两个离子组成，这样就可以将N-Al对中的偶极矩表示为图4所示的偶极矩(由箭头表示)的合成.以上述分析为基础，AlN超胞中总的电偶极矩即为结构中所有N-Al 对中的偶极矩之和.值得注意的是，在超胞中，处理最上方或者最下方的N-Al的偶极矩时，根据所建超胞的实际情况需要增加或者减少一个晶格常数项，而该项在两种超胞体积不同的情形下非常重要，在其他文献中闪锌矿与纤锌矿采用同一体积，会使得这一项两两相减而正好消掉，因此被式(8)所忽视，我们用图5来说明.

(a) N面 (b) Al面

在计算图5(a)所示的黑色方框中N-Al对的偶极矩时，由于N原子已经位于晶胞的最上方，因此计算偶极矩时所需的三个Al原子就必然位于晶胞之外，根据对称性，超胞外Al原子的Z坐标就需要由晶胞中最下方的Al原子的Z坐标加上晶格常数c得来，而且由于需要三个晶胞外的Al原子来计算偶极矩，因此相比直接利用式(8)计算，黑框中的N-Al对的偶极矩就增加了ΔPdipol，可写为，

(9)

式(9)中：ZAl为最下方的Al原子的Z坐标， 为纤锌矿超胞[0001]方向的晶格参数，对于整个纤锌矿超胞中的偶极矩，则表示为，

(10)

因此最终纤锌矿结构中的自发极化计算修正为，

(11)

cZB为闪锌矿超胞[0001]方向的晶格参数,GaN、ZnO的自发极化计算的修正与上述情况相似，只不过在ZnO中由于O为+6价，此时需要把式(11)中的3/4更换为2/4,本文计算中所建闪锌矿及纤锌矿超胞模型均为图5(a)的情形，即N、O原子位于最上方.因此根据修正后的式(11)，计算得到的结果如表5所示，实现了与Berry phase方法得到的结果一致．对于图5(b)中所示的Al面结构，其修正与N面相似，不再赘述.

2.3 利用电荷重心自发极化

前面利用Berry phase及MLWF方法计算自发极化时，都需要计算闪锌矿参照结构中的极化值，然后纤锌矿与闪锌矿形式上的极化值之差为自发极化，这样计算起来稍显复杂，分析自发极化的形成也不直观.MLWF方法可形象地将整个晶体分为局域的带正电的离子与带负电的Wannier中心，我们发现在当前建模条件下，利用纤锌矿结构的对称性及Wannier中心也是几乎对称分布的特点，可以方便地确定正负离子的重心，然后将其看成是经典静电学中的正负中心点电荷，带电量分别为+8e、-8e，然后根据

(12)

可以直接得到纤锌矿结构中的自发极化，而不用再计算闪锌矿参照结构中的极化，式(12)中q=-8e，为负中心点电荷带电量.这样更能直观地解释自发极化的形成.下面以AlN结构中一个重复单元为例进行说明.图6给出了AlN闪锌矿及纤锌矿结构中的键长及Wannier中心与N原子之间的距离.在AlN结构中，N原子轨道sp3杂化，与周围四个Al原子成键，根据MLWF的特点，可以认为图6中每个Al带电量为0.75.在闪锌矿结构中，由于四个N-Al键的键长都相同，N原子位于正面体的中心位置，因此正电荷的重心位于N原子上；而四个Wannier中心也是对称的分布在N原子周围，其电荷重心也位于N原子上，因此整体上正负电荷重心重合，不存在电偶极矩，也就没有自发极化.在纤锌矿结构中，沿[0001]方向的键长大于其余三个键长，因此四个Al原子的正电荷重心偏向N原子上方，导致最后总的正电荷重心处在N原子上方；此外四个Wannier中心的电荷重心位置也偏离了N原子，这是由于[0001]方向上Wannier中心比其余三个Wannier中心更靠近N原子，使得整个负电荷重心处于N原子的下方.因此结构中整体上正负电荷重心明显分离，产生了电偶极矩，方向竖直向上，与[0001]方向相反，这与表4得到的分析结果完全一致.

图6 AlN两种结构中键长及Wannier中心

为了分析因正负电荷中心分离产生的偶极矩大小，根据结构的对称性计算了图6(b)所示纤锌矿结构的正负电荷的重心位置(仅考虑Z坐标)，以及据此计算得来的自发极化，如表6所示，由于Ga、Zn原子的d电子局域在Ga、Zn原子的位置，对极化的贡献很小，因此计算时不考虑d电子.

表6 纤锌矿结构正负电荷重心位置、自发极化

首先从自发极化的计算结果可以看到与利用MLWF方法的结果几乎一致，说明了分析正负电荷重心过程的合理性，也说明利用这种通过正负电荷重心计算自发极化的方法可以不用再构建闪锌矿参照结构，符合人们传统直观的认识.从正负电荷重心之间的间距Δr可以看出，AlN在三种晶体中正负电荷重心间距最大，达到GaN的2.6倍，表明了AlN较强的极性.

3 结论

根据现代极化理论，通过构建闪锌矿参照模型及纤锌矿计算模型，利用Berry phase方法及MLWF方法系统地计算了纤锌矿结构的AlN、 GaN及ZnO三种晶体的自发极化，与其它报道进行了比较.从电子部分及离子部分的贡献分析了自发极化的形成，发现在AlN中电子部分的贡献占主导地位，而GaN及ZnO中则已离子部分的贡献为主.同时发现其他文献报道中所用计算方法的不足，会导致计算结果偏小，指出这是由于将闪锌矿及纤锌矿超胞采用同一体积所导致的，从电偶极矩的角度出发分析了原因，并给出了修正公式.

[1] Strite S,Morkoc H.GaN,AlN and InN:A review[J].Journal of Vacuum Science amp; Technology B,1992,10(4):1 237-1 266.

[2] Ozgur U,Alivov Y I,Liu C,et al.A comprehensive review of ZnO materials and devices[J].Journal of Applied Physics,2005,98(4):1-103.

[3] Nakamura S,Iwasa N,Senoh M,et al.Hole compensation mechanism of p-type GaN films[J].Japanese Journal of Applied Physics,1992,31(5A):1 258-1 266.

[4] Taniyasu Y,Kasu M,Makimoto T.An aluminium nitride light-emitting diode with a wavelength of 210 nanometres[J].Nature,2006,441(7091):325-328.

[5] Nakamura S.The roles of structural imperfections in InGaN-based blue light-emitting diodes and laser diodes[J].Science,1998,281(5379):956-961.

[6] 孔月婵,郑有炓.Ⅲ族氮化物异质结构二维电子气研究进展[J].物理学进展,2006,26(2):127-145.

[7] 薛丽君,刘 明,王 燕,等.AlGaN/GaN异质结极化行为与二维电子气[J].半导体技术,2004,29(7):63-65.

[8] 申 晔,邢怀中,俞建国,等.极化诱导的内建电场对Mnδ掺杂的GaN/AlGaN量子阱居里温度的调制[J].物理学报,2007,56(6):3 453-3 457.

[9] Kozodoy P,Smorchkova Y P,Hansen M,et al.Polarization-enhanced Mg doping of AlGaN/GaN superlattices[J].Applied Physics Letters,1999,75(16):2 444-2 446.

[10] Allen M W,Miller P,Reeves R J,et al.Influence of spontaneous polarization on the electrical and optical properties of bulk,single crystal ZnO[J].Applied Physics Letters,2007,90(6):301-373.

[11] 马继昭.极化效应对紫外发光二极管光电特性影响的研究[D].南京:南京大学,2013.

[12] 董可秀.Ⅲ族氮化物的极化效应及其在光电子器件中的应用[D].南京:南京大学,2013.

[13] Marzari N,Vanderbilt D.Maximally localized generalized Wannier functions for composite energy bands[J].Physical Review B,1997,56(20):12 847-12 865.

[14] Souza I,Marzari N,Vanderbilt D.Maximally localized Wannier functions for entangled energy bands[J].Physical Review B,2002,65(3):321-325.

[15] Vanderbilt D,King-smith R D.Electric polarization as a bulk quantity and its relation to surface charge[J].Physical Review B Condensed Matter,1993,48(7):4 442-4 455.

[16] Giannozzi P,Baroni S,Bonini N,et al.Quantum Espresso:A modular and open-source software project for quantum simulations of materials[J].Journal of Physics Condensed Matter An Institute of Physics Journal,2009,21(39):1-19.

[17] Mostofi A A,Yates J R,Lee Y S,et al.wannier90:A tool for obtaining maximally-localised Wannier functions[J].Computer Physics Communications,2008,178(9):685-699.

[18] Mostofi A A,Yates J R,Pizzi G,et al.An updated version of wannier90:A tool for obtaining maximallylocalised Wannier functions[J].Computer Physics Communications,2014,185(8):2 309-2 310.

[19] Bernardini F,Fiorentini V,Vanderbilt D.Spontaneous polarization and piezoelectric constants of III-V nitrides[J].1997,56(16):10 024-10 027.

[20] Gopal P,Spaldin N A.Polarization,piezoelectric constants,and elastic constants of ZnO,MgO,and CdO[J].Journal of Electronic Materials,2006,35(4):538-542.

[21] Laehnemann J,Brandt O,Jahn U,et al.Direct experimental determination of the spontaneous polarization of GaN[J].Physical Review B,2012,86(8):1-5.

【责任编辑：陈佳】

First-principlesstudyofspontaneouspolarizationofwurtziteAlN,GaNandZnO

NIU Hai-bo1, ZHU You-zhang1, LI Guan-qiang2

(1.Department of Physics, Xi′an Jiaotong University City College, Xi′an 710018, China; 2. School of Arts and Sciences, Shaanxi University of Science amp; Technology, Xi′an 710021, China)

By using Berry phase and maximally localized Wannier functions methods based on the modern polarization theory,the spontaneous polarization of wurtzite AlN,GaN and ZnO are calculated respectively.The origin of spontaneous polarization is studied from the polarization variation of ionic and electronic part.It is found that the spontaneous polarization of AlN is primarily from the electronic part,while the spontaneous polarization of GaN and ZnO is mainly from the ionic part.Since the computational model and reference model have a same volume in the literature,it is found that the result is reduced compared with our result.On the basis of the discussion of local dipole,a correction formula is given to make the calculation more reasonable.Using the charge depth of the formula unit,we also proposed a new method to directly calculate the spontaneous polarization of wurtzite structure without the computation of reference structure.The production of the spontaneous polarization can be intuitively explanation in terms of this method.

wurtzite structure； spontaneous polarization； Wannier center； first principles

2017-08-15

陕西省教育厅专项科研计划项目(16JK2099)

牛海波(1981-)，男，山西运城人，副教授，博士，研究方向：宽禁带半导体中的极化场性质

2096-398X(2017)06-0171-08

O469

A