巧解多元函数的最值
2017-12-02张海涛
张海涛
(山西大同大学数学与计算机科学学院,山西大同037009)
巧解多元函数的最值
张海涛
(山西大同大学数学与计算机科学学院,山西大同037009)
多元函数的最值问题,由于技巧性较强又灵活多变,掌握起来有一定的难度,对这类问题采取灵活的算法,避免了繁琐的计算,为多元函数最值的学习提供一个参考。
多元函数;极值;最值;条件极值
最值问题一直是各阶段学习的重点和难点,而多元函数的极值又因为其技巧性强又灵活多变,是高等数学中的难点知识。文献[1-3]中给出的方法对于某些函数计算量又颇大,本文对此类问题给出了灵活的方法,避免了繁琐的计算,对多元函数最值的学习提供一个参考。
1 多元函数极值的定义及最值的常规解法
极值定义:如果二元函数z=f(x,y),对于点(x0,y0)的某一领域内的所有的点,总有:
f(x,y)<f(x0,y0),(x,y)≠(x0,y0),则称f(x0,y0)是函数f(x,y)的极大值;如果有:
f(x,y)>f(x0,y0),(x,y)≠(x0,y0),则称f(x0,y0)是函数f(x.y)的极小值。
函数的极大值与极小值统称为极值,使函数取得极值的点称为极值点。
如果f(x,y)在(x0,y0)的某个领域内有且仅有一个极大值而无极小值,则此极大值就是最大值。如果有且仅有一个极小值而无极大值,则此极小值就是最小值。本文讨论的最值即是此种类型。因此文中的多元函数的最值问题就转化为多元函数的极值问题。
定理1(极值存在的充分条件)如果函数f(x,y)在点(x0,y0)的某一领域内有连续的二阶偏导数,且(x0,y0)是它的驻点,设

记:A=p(x0,y0),B=f″xx(x0,y0),
(1)如果A<0,B<0,则f(x0,y0)是极大值;
(2)如果A<0,B>0,则f(x0,y0)是极小值;
(3)如果A>0,则f(x0,y0)不是极值;
(4)如果A=0,则f(x0,y0)是否为极值需另法判断。
2 巧解多元函数的最值
2.1 利用隐函数的偏导
问题1设x是s和t的二元函数,且2s2+2t2+x2+st+sx+tx=4,求x的最大值。
分析:如果把x解出来再去求极值,计算量大,过程复杂,因此,可以采用求隐函数的方法,这就避免了求根式函数的极限。
解:方程两边分别对s和t求偏导得:
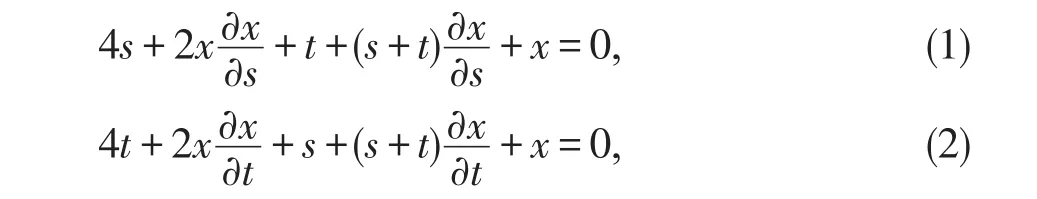
这个题还可以用初等解法:把方程看作是s的方程,显然有解,由此得判别式Δ=(t+x)2-4×2×(2t2+x2+tx-4)≥0,解得 7x2+6tx+15t2-32≤0,同理,把方程看作是t的方程得Δ=36x2-60(72x2-32)≥0,解得x2≤5,从而x的最大值为且这个最值是能够达到的。
2.2 转化为条件极值求最值
分析:这个题当然可以直接求导,但是因为是分式函数,形式比较复杂,为了简化运算,不妨把它转化成条件极值。
解:把问题转化为下面的形式

其中a是大于0的常数。
对各变量分别求偏导得:

2.3 利用几何意义求最值
问题3求函数
x=的最小值。
解:函数分别对s和t求偏导并令偏导为0可得:
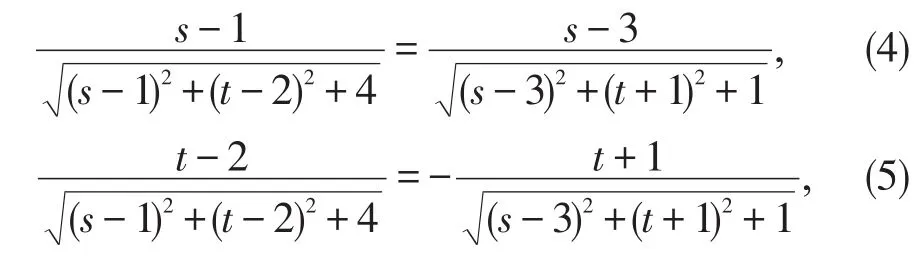
(4)(5)两式相除可得s-t-1=2s-3t+6,(4)(5)两式平方相加得到
4[(s-3)2+(t+1)2+1]=(s-1)2+(t-2)2+4,由此可知:
s=t=0,代入函数得即为所求的最小值。上面是一个常规的解法,计算量较大,下面给出一个几何解法。
其几何意义是:点A(s,t,0)到P1(1,2,2),P2(3,-1,-1)距离之和的最小值,易知,当P1AP2在一条直线上时x最小,故可取A在P1P2上,因此x的最小值就是P1P2的长度,所以x的最小值为:
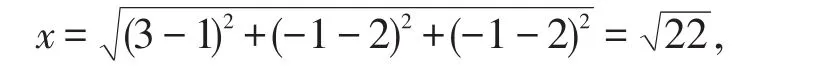
显然,这个解法要比标准解法简单易算。
[1]张禾瑞,郝炳新.高等代数[M].4版.北京:高等教育出版社,1999.
[2]同济大学应用数学系.线性代数[M].4版.北京:高等教育出版社,2003.
[3]高志强,庞彦军.线性代数[M].北京:科学出版社,2016.
〔责任编辑 高海〕
The Maximum Value of Multivariate Function Solution
ZHANG Hai-tao
(School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009)
As to the maximum value problem of multivariate function,because the skills are a strong and flexible,to master them are difficult,this paper adopts a flexible algorithm for this kind of problem,avoiding the tedious computation,which provides a refer⁃ence for the value of multivariate function learning.
multivariate function;extreme value;maximum value;conditional extremum
O013
A
1674-0874(2017)05-0001-02
2017-03-16
张海涛(1974-),女,山西阳高人,硕士,副教授,研究方向:高等数学教学。
