一种影响空间相机成像的制冷机微振动分析方法

2017-12-01李世其刘世平

宇航学报 2017年11期

关键词：制冷机扰动光学

张恒，李世其，刘世平，王跃,2，张哲

(1. 华中科技大学机械科学与工程学院，武汉 430074；2. 北京空间机电研究所，北京 100094)

一种影响空间相机成像的制冷机微振动分析方法

张恒1，李世其1，刘世平1，王跃1,2，张哲1

(1. 华中科技大学机械科学与工程学院，武汉 430074；2. 北京空间机电研究所，北京 100094)

针对空间制冷机微振动对光学遥感器成像质量难以准确评估的问题，提出一种制冷机-空间相机的集成建模分析与试验验证方法。该方法建立了系统的集成分析模型，实现了微振源-相机结构传递-光路模型的分析过程。首先，利用一种制冷机的刚性安装测试和自由悬吊测试获取制冷机的扰动载荷。然后，采用一种力过滤方法改进传统的扰动分析过程。最后，通过集成有限元分析计算光学系统调制传递函数，得出制冷机微振动对空间相机成像的影响。分析结果表明，这种方法能更精确辨识制冷机微振动及其传递特性，从而能准确分析空间相机光学载荷的稳定性。

空间相机；微振动；耦合扰动分析；集成模型；微振动试验

0 引言

随着空间遥感任务对精度要求的提高，空间平台上的有效载荷对振动环境也提出了更高的要求[1-2]。由空间相机中机构运转而引发的一类微振动对相机成像的影响越来越受到重视，微振动对航天器机理研究正日益成为航天器研制的热门领域。因此，亟需从单机、分系统、系统各级层开展研究和设计工作[3]。

脉冲管制冷机微振动是光学遥感载荷在轨工作状态下的重要振源。为了量化其作用在空间相机上动态扰动的影响，有必要精确建立制冷机时域和频域扰动模型，用这种模型去分析相机结构关键点的振动响应及评估微振动对光学系统成像质量退化的影响。常用的方法包括将试验测试数据直接用于仿真分析的经验模型方法与根据物理参数建立振源扰振特性的机理模型方法。其中前者更为接近真实情况，但缺点是数据的时间长度不足；后者可以生成任意时长的扰振载荷数据，但与实际试验结果存在明显差别。对于脉冲管制冷机的振动分析问题，国内外学者进行了一系列研究工作[4-7]。

微振源与柔性支撑的耦合特性研究是微振动机理研究的重要基础，直接决定了微振动源扰振特性的识别与各层级研究输入载荷的精确性。耦合扰动分析是分析微振源安装在柔性支撑结构上时输出的微振动特性[8]。传统的刚性界面支撑试验并不能真实地模拟微振动源与空间相机接口的边界条件，因此，有必要建立能综合反映支撑结构刚度、质量特性的组合体耦合动力学模型，并分析微振源与柔性支撑的耦合作用对于微振动输出特性的影响机理。常用的耦合特性研究方法包括动质量法[9]、试验载荷过滤系数法[10-11]等。

微振动扰动通常会引起光学系统及光学元件抖动而使其不能保持设计时的状态，从而导致像面像质的退化[12]。一方面，微振动造成各光学元件刚体位移和面形变化；另一方面，微振动引起视轴振动造成视轴漂移和视轴颤振[13-14]。当光学系统或者光学元件发生微振动时，像点位置必然发生变化，原本聚集在一点的成像，变成散落在不同位置的成像，从而造成能量分布范围扩大，致使像面光强对比度降低、分辨率下降[15-16]。

基于以上分析，为了准确评估制冷机微振动对空间相机成像质量的影响，本研究提出了一种光-机集成分析方法。针对其所涉及的微振动建模、测试与分析开展相关研究，为更好地检验空间相机微振动，发展高分辨率对地观测卫星系统发挥重要作用。

1 基本理论与模型建立

1.1制冷机扰动源模型

脉冲管制冷机是一种冷头中不包含运动器件的低振动、长寿命、高可靠性核心部件。为进一步降低振动输出，脉冲管制冷机常采用一组背对背式的线性双活塞压缩机。然而，对置的电机(活塞)存在不同的磨损、摩擦系数、弹性系数、密封间隙、磁体强度等等，这些不对称因素将导致双活塞压缩机失去原有的平衡设置，从而使制冷机不可避免的引入微振动。本研究的典型线性驱动压缩机如图1所示，其压缩机采用线性驱动、活塞对称布置、板弹簧支撑和间隙密封技术。

探索制冷机扰动模型的方法包含两类：机理模型与经验模型。根据模型的物理参数，可将制冷机的扰动模型简化为两自由度动力学系统，其简化模型如图2所示，系统运动方程为式(1)。

(1)

(2)

式(1)中:m为活塞的质量；c为阻尼系数；k为活塞支撑弹簧的刚度；x为活塞的位移；f为活塞的电磁驱动力，下标1,2为活塞的编号；下标g表示与气体工质相关的量。将式(1)转换到频域可以得到式(2)。在理想情况下，对置式的直线电机的整体振动输出为0。但在实际中由于存在加工制造误差、装配误差、驱动电压波动等原因，必然会存在一定的振动输出。

为进一步获取制冷机的真实振动输出，常采用一种基于测试数据的经验模型方法。假设扰动由离散频率正弦谐波组成，时域扰动力模型可表示为

fk(kΔt)=P0sin(ωkΔt+φ)+

(3)

式中：P0为驱动频率ω的力幅值，fn为高次谐波系数。根据时域信号的离散傅里叶变换，计算频域扰动力Fk为

(4)

两种建模方法均可用作制冷机的扰动模型，为了真实的反映制冷机工作过程对相机系统成像造成的影响，本研究采用制冷机的经验扰动模型用于分析计算。

1.2局部耦合扰动分析模型

在获得了制冷机在刚性试验设置的扰动模型后，工程上是将测试的扰动响应直接输入到整机有限元模型中进行仿真计算。然而这种方式并没有考虑空间平台与制冷机之间的耦合关系。因为在固定边界条件下测得的扰动响应的结果不同于耦合边界环境。

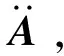
(5)

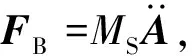
(6)

在微振源与支撑结构的耦合系统中，连接处的加速性(动质量的逆矩阵)对于耦合扰动分析具有重要作用。则变换矩阵Gf可表示为

(7)

式中：AC(ω)为制冷机激励点的加速度响应，AS(ω)为耦合结构激励点的加速度响应。

1.3微振动整星传递模型

由频域内输入-输出原则，估计空间光学载荷平台的振动响应

Z(ω)=GZF(ω)F(ω)

(8)

式中：ω为频率，Z为预估性能向量，F为制冷机扰动载荷向量，GZF为结构的传递函数。根据非耦合扰动分析方法，计算有效载荷的性能谱密度为

(9)

式中：ΦZZ为输出功率谱密度矩阵，ΦFF为制冷机的扰动谱密度矩阵。然而刚性测试扰动谱不同于真实的耦合边界条件，这类扰动谱通过空间相机传递函数ΦZF获得的输出功率谱并不能反映光学载荷的真实输出。

根据第1.2节的力过滤方法，可得耦合条件下制冷机的扰动谱密度为

(10)

根据式(10)，耦合条件下有效载荷的性能谱密度为

(11)

1.4光路模型与光学分析

相机光学系统构型如图4所示，相机采用RC(Ritchey Chretien,RC)双反系统加校正镜组的光学系统方案。入射光线经主镜和次镜反射后通过主镜中心孔到达分光镜，一部分光被分光镜反射经由可见光透镜组到达可见光焦面，一部分光穿过分色片后被折转镜反射，经由红外透镜组到达红外成像焦面。

微振动造成相机光学器件的刚体位移可定义为相对其中心坐标系的位移和转角。在光学分析中，光学表面定义在局部顶点坐标系中，光学表面的刚体位移定义为相对顶点坐标系的位移和转角。分析微振动对相机光学成像的影响，需要将结构响应转化成光学元件的面形变化、相对位置偏离以及光轴偏转等物理量。

2 相机系统的集成分析与性能评估

微振动试验的总体方案和流程如图5所示，包含单机级、分系统级和系统级试验。单机级试验是通过试验了解微振源的动态特性，包括扰动力的幅值大小和频率分布，从而确保仿真分析在输入端的正确性。分系统级振动试验包含两方面，制冷机与接口的局部传递特性测试与整星结构的传递特性测试，其测试结果主要用于有限元模型的验证和修正，从而确保微振动的传递特性符合真实情况。系统级试验是采用光-机集成系统作为微振源到光学器件最终成像的全链路分析测试，从而直接了解微振动对最终成像质量的影响情况。本研究以调制传递函数(Modulation transfer function, MTF)为指标分析微振动对相机成像的影响。

通过上述3个层次的试验分析，对空间相机微振源、微振动的结构传递以及最终的成像质量进行全面系统的分析和评价，以有效校验仿真分析和设计结果，保障像质清晰、准确和可靠。

3 测试试验与模型校验

3.1制冷机微振动测试

为了获得制冷机扰动，分别对制冷机处于刚性安装与自由-自由状态下的微振动进行测试。刚性安装是根据制冷机在实际工作时的方式设计安装夹具，测试时将制冷机整机固定在夹具中，如图6(a)所示。压缩机悬臂安装设置，采用三向力传感器测得压缩机接口处的扰动力载荷。自由悬吊设置如图6(c)所示，采用三向加速度计测量压缩机的加速度响应，根据已知悬吊件的质量将加速度转换为扰动力。

图6(b)和6(d)中显示了两类边界条件下压缩机在驱动方向(z向)的振动输出。由图6可知，驱动频率的振动幅值最大；自由状态比刚性安装的扰动力大，这是由刚性边界条件下制冷机与支撑结构的耦合效应以及自由状态下计算误差所引起的。

3.2相机系统传递特性测试与验证

刚性安装条件下测试制冷机扰动时，制冷机接口表面为静止状态，这种无限阻抗的边界不同于制冷机与空间结构耦合的实际工作情况。本研究根据第1.2节的耦合理论模型，采用“力过滤”方法得到制冷机与支撑结构的局部耦合关系，从而修正制冷机的单机试验结果。

根据制冷机压缩机的刚体模型与空间相机结构的有限元模型，估计制冷机驱动点加速度AC(ω)和支撑结构驱动点加速度AS(ω)。本研究主要考虑压缩机三个移动方向的力过滤分析，预估制冷机驱动点加速度如图7(a)所示。为了获得支撑结构驱动点加速度，采用空间相机有限元模型，对压缩机中心施加单位力，获得安装接口的动响应如图7(b)所示。

基于压缩机刚体模型驱动点加速度与相机有限元模型驱动点加速度，获得力过滤结果如图8所示。

由图8可知，力过滤实质是对刚性边界测试结果的修正，使其更接近柔性连接情况。

对相机进行整机的鉴定级振动试验，主要用于验证相机主体的基频特性以及相机关键部位的放大率。由于光学系统校正组光学元件尺寸较小且光学结构刚度足够高，完全可以视为一体，所以重点分析口径较大的主镜。试验过程中，将相机主体通过振动支架安装在振动台上，按Z、X、Y三个方向进行振动测试。选取主镜中心作为关键测点，以振动台测点作为控制点，将关键测点与控制点的加速度的比率作为振动台到相机结构的传递率。试验完成后对试验数据进行处理，并与整机仿真结果进行了对比分析，如图9所示。由图9可知，仿真数据与试验测试数据有较高吻合度，校验了整机仿真模型的有效性。

4 光学性能分析与评价

光学模型是联系光学元件机械微位移与像质退化的桥梁。由于相机主、次镜尺寸较大，结构刚性相对较小，其产生的面形变化(离焦和像散)和刚体位移(平移和倾斜)是影响像质的主要成分。首先，将微振动试验数据输入相机有限元模型进行仿真计算，得到主、次镜节点的位移响应数据。为了实现其对光学系统的影响分析，在常用的光学设计软件Zemax中采用Zernike多项式对变形后的镜面进行拟合，将拟合后的各项系数输入Zemax，从而直观地考察微振动作用下系统的像质变化。

表1 主、次镜镜面前5项Zernike多项式系数Table 1 The first five coefficients of Zernike polynomial of the primary and secondary mirror

根据获取的镜面形变数值分析结果，拟合后主、次镜镜面的前5项Zernike系数见表1。其中，前三项分别对应刚体平移、X向倾斜及Y向倾斜。由表1可知，微振动对镜面的刚性位移影响较大，对面形影响小。将拟合分析结果导入Zemax中分析成像系统MTF变化，如图10所示。图10(a)为原系统MTF曲线，图10(b)为变形后系统的MTF曲线。由图10可知，镜面变形对MTF影响非常小，对应于Nyquist频率56 lp/mm处MTF下降了0.0018%，由微振动引起的镜面面形变化可以忽略不计。

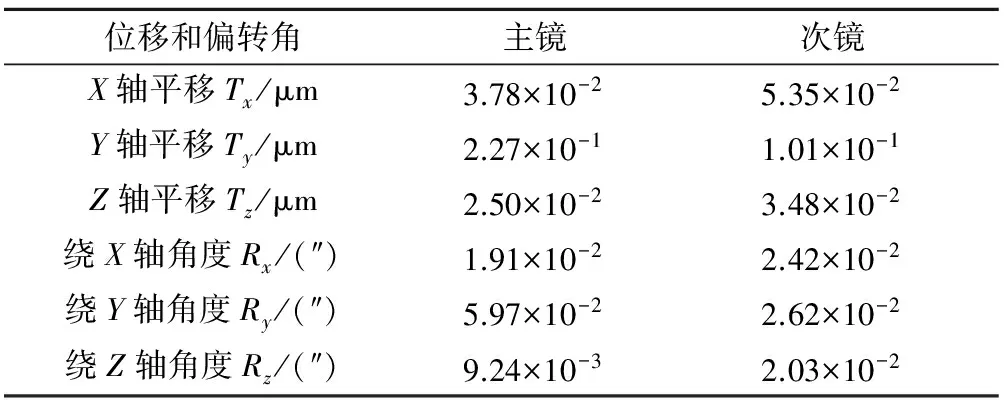
表2 主镜、次镜偏离安装位置最大值Table 2 The deviated maximum value of the primary and secondary mirror

另一方面，微振动引起相机主、次镜产生刚体平移，从而导致相机光轴发生偏角变化。为了分析光学元件偏离理想安装位置的姿态变化，本研究选取相机的主承力结构作为参照，分析主、次镜在微振动载荷作用下的平移和刚性转动，其偏离安装结构的结果见表2。由此可知，微振动主要引起主、次镜发生横向偏移与绕横向的转动，从而对相机像质产生影响。表3列出了系统5个视场下光学元件在空间频率56 lp/mm处的MTF均值。子午方向(T)和弧矢方向(S)分别下降了0.161%和0.166%，可见由于元件刚体位移引起的成像质量下降大于面形变化引起的成像质量下降。

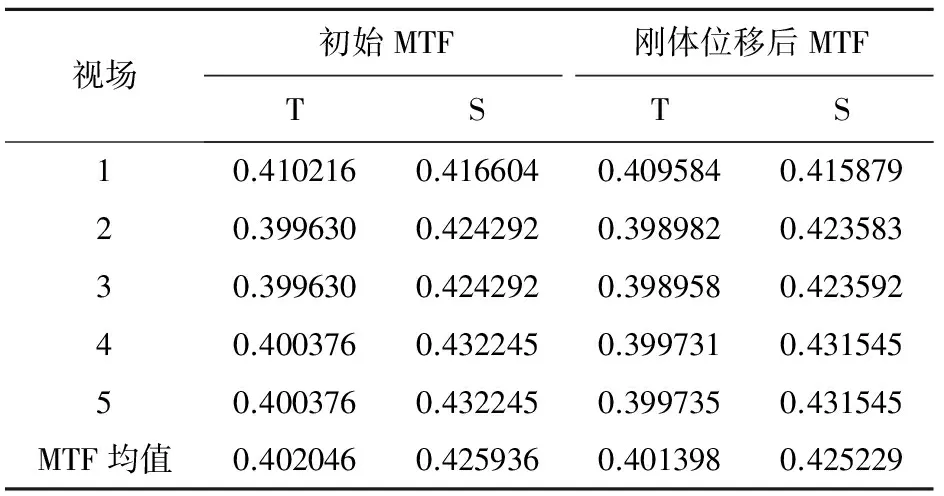
表3 产生刚体位移前后MTF的值Table 3 The MTF value change before and after rigid body motion

5 结论

为了解微振动对相机光学系统成像质量的影响方式，明确在轨机械微振动对成像质量的影响程度，提出了一种空间相机的集成建模分析与试验验证方法。基于空间制冷机微振动试验，采用局部耦合扰动分析修正制冷机单机试验结果，从而保证微振动载荷输入端的准确性。结合相机整机有限元分析模型与鉴定级振动试验，校验整机仿真模型的有效性。最后，通过仿真分析获取主、次镜节点的微位移，输入到光学分析软件，分析出微振动对光学成像质量的影响。试验与仿真分析结果表明，微振动下光学元件的刚体位移是引起系统成像质量下降的主要因素。通过本研究的微振动评估与分析方法，可为相机结构的优化改进及微振动抑制措施等提供参考。

[1] 张庆君, 王光远, 郑钢铁. 光学遥感卫星微振动抑制方法及关键技术[J]. 宇航学报, 2015, 36(2):125-132.[Zhang Qing-jun, Wang Guang-yuan, Zheng Gang-tie. Micro-vibration attenuation methods and key techniques for optical remote sensing satellite[J]. Journal of Astronautics, 2015, 36(2):125-132.]

[2] 徐鹏, 黄长宁, 王涌天, 等. 卫星振动对成像质量影响的仿真分析[J]. 宇航学报, 2003, 24(3):259-263.[Xu Peng, Huang Chang-ning, Wang Yong-tian, et al. Modulation transfer function in push-broom camera limits resulting from mechanical vibration[J]. Journal of Astronautics, 2003, 24(3):259-263.]

[3] 庞世伟, 潘腾, 毛一岚, 等. 某型号卫星微振动试验研究及验证[J]. 航天器环境工程, 2016, 33(3):305-311.[Pang Shi-wei, Pan Teng, Mao Yi-lan, et al. Study and verification of micro-vibration test for a satellite[J]. Spacecraft Environment Engineering, 2016, 33(3):305-311.]

[4] 白绍竣, 唐绍凡, 聂云松, 等. 空间机械制冷机微振动研究[J]. 航天返回与遥感, 2013, 34(6):51-56.[Bai Shao-jun, Tang Shao-fan, Nie Yun-song, et al. Investigation of micro-vibration of space cryocoolers[J]. Spacecraft Recovery amp; Remote Sensing, 2013, 34(6):51-56.]

[5] Tomaru T, Suzuki T, Haruyama T, et al. Vibration analysis of cryocoolers[J]. Cryogenics, 2004, 44(5):309-317.

[6] Riabzev S V, Veprik A M, Vilenchik H S, et al. Vibration generation in a pulse tube refrigerator[J]. Cryogenics, 2009, 49(1):1-6.

[7] Oh H U, Lee K J, Jo M S. A passive launch and on-orbit vibration isolation system for the spaceborne cryocooler[J]. Aerospace Science and Technology, 2013, 28(1):324-331.

[8] Zhang Z, Aglietti G S, Ren W J. Coupled microvibration analysis of a reaction wheel assembly including gyroscopic effects in its accelerance[J]. Journal of Sound and Vibration, 2013, 332(22):5748-5765.

[9] Elias L M, Miller D W. A coupled disturbance analysis method using dynamic mass measurement techniques[C]. The 43rd Annual AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, USA, April 22-25, 2002.

[10] Elias L, Dekens F, Basdogan I, et al. Methodology for modeling the mechanical interaction between a reaction wheel and a flexible structure[C].SPIE Astronomical Telescopes and Instrumentation Conference, Waikoloa, USA,August 2003.

[11] Addari D, Aglietti G S, Remedia M. Experimental and numerical investigation of coupled microvibration dynamics for satellite reaction wheels[J]. Journal of Sound and Vibration, 2017, 386(6):225-241.

[12] 王跃, 王博, 刘世平, 等. 空间红外遥感相机制冷机微振动对MTF影响分析[J]. 航天返回与遥感, 2015, 36(3):61-68.[Wang Yue, Wang Bo, Liu Shi-ping, et al. Analysis of effect of cryocooler’s micro vibration on MTF for space infrared remote sensing camera[J]. Spacecraft Recovery amp; Remote Sensing, 2015, 36(3):61-68.]

[13] Basdogan I, Elias L M, Dekens F, et al. Predicting the optical performance of the space interferometry mission using a modeling, testing, and validation methodology[J]. Journal of Vibration and Acoustics, 2007, 129(2):148-157.

[14] 贺小军, 王金玲, 金光. 相机摆放方式对推扫成像试验的影响分析[J]. 宇航学报, 2012, 33(9):1354-1360.[He Xiao-jun, Wang Jin-ling, Jin Guang. Analysis on effect of camera setting way on pushbroom imaging experiment[J]. Journal of Astronautics, 2012, 33(9):1354-1360.]

[15] 王红娟,王炜,王欣,等. 航天器微振动对空间相机像质的影响[J]. 光子学报, 2013, 42(10): 1212-1217.[Wang Hong-juan, Wang Wei, Wang Xin, et al. Space camera image degradation induced by satellite micro-vibration[J]. Acta Photonica Sinica, 2013, 42(10): 1212-1217.]

[16] 朱俊青,沙巍,陈长征,等. 大口径空间相机像质的微振动频率响应计算[J]. 光学精密工程, 2016, 24(5): 1118-1127.[Zhu Jun-qing, Sha Wei, Chen Chang-zheng, et al. Frequency response of imaging quality by micro-vibration for large-aperture space-borne telescope[J]. Optics and Precision Engineering, 2016, 24(5): 1118-1127.]

AnAnalysisMethodofEffectofCryocoolerMicrovibrationonSpaceCameraImaging

ZHANG Heng1, LI Shi-qi1, LIU Shi-ping1, WANG Yue1,2, ZHANG Zhe1

(1. School of Mechanical Science amp; Engineering, Huazhong University of Science and Technology, Wuhan 430074, China; 2. Beijing Institute of Space Mechanics amp; Electricity, Beijing 100094, China)

Aiming at accurately evaluation of image quality on an optical remote camera, an integrated modeling analysis and experimental verification method of microvibration induced by space cryocooler is proposed. This method establishes the system model and realizes the analysis process of microvibration source-camera transfer-optical model. Firstly, a blocked test with the coolerhardmounted and a free-free dynamic test by suspending the cryocooler are performed to obtain the disturbance data. Then, the force filter method is used to improve the traditional disturbance analysis. Finally, the performance of optics represented by MTF change is calculated by integrating finite element analysis. The results show that this method can accurately identify microvibration and its transfer characteristics, which can be used to accurately analyze the stability of optical load on space camera.

Space camera; Microvibration； Coupled disturbance analysis； Integrated model； Microvibration test

V414

1000-1328(2017)11- 1226- 08

10.3873/j.issn.1000- 1328.2017.11.012

2017- 03- 21;

2017- 09- 11

国家科技重大专项

张恒(1988-)，男，博士生，主要从事空间相机微振动测试与分析研究。

通信地址：武汉市洪山区珞喻路1037号华中科技大学东八楼蒋震中心420室(430074)

电话：(027)87557883；13627266917

E-mail:zh20061100068@163.com

李世其(1965-)，男，博士，教授，主要从事工程结构及机械系统动态设计研究。本文通信作者。