执行机构故障的航天器姿态容错控制

耿云海，金荣玉，陈雪芹，李冬柏

(哈尔滨工业大学卫星技术研究所，哈尔滨 150001)

执行机构故障的航天器姿态容错控制

耿云海，金荣玉，陈雪芹，李冬柏

(哈尔滨工业大学卫星技术研究所，哈尔滨 150001)

针对航天器执行机构(飞轮)故障的姿态控制问题，基于线性变参数(LPV)系统设计鲁棒变增益PID容错控制。考虑转动惯量随时间变化和执行机构乘性故障，将航天器姿态动力学转化为不确定LPV系统。设计控制器时，利用仿射二次稳定的方法降低控制算法的保守性，引入保性能控制保证系统的鲁棒性。仿真结果表明，控制方法是有效的。

航天器姿态控制；容错控制；执行机构故障；线性变参数(LPV); 鲁棒变增益控制

0 引 言

在轨航天器由于长时间工作在失重、高低温和强辐射等恶劣环境中，各种各样的故障伴随而生，其中执行机构和敏感器发生故障最为常见[1]。所以，针对航天器执行机构故障，研究姿态容错控制是至关重要的。到目前为止，航天器姿态容错控制方面，已经有一定的研究成果。文献[2]研究了基于PD学习型观测器的系统故障重构方法，能够快速精确地重构航天器执行机构故障。文献[3]在执行机构输出受限的情况下，根据从状态观测器得到的故障信息来重构控制器。文献[4]针对航天器外部干扰和执行机构发生乘性故障，利用故障观测器获得的故障信息设计容错控制器。文献[5]针对未知的执行机构故障，利用滑模观测器和自适应故障估计法获得故障信息，并据此设计容错控制器，利用Lyapunov方法进行稳定稳定性分析。文献[6]在允许少量飞轮完全失效的情况下，设计了自适应反步容错控制器。文献[7]研究了不依赖于角速度和故障信息的姿态容错控制。文献[8]针对执行器和敏感器故障，分别研究了基于H∞的容错控制。

线性变参数(Linear parameter varying，LPV)系统是一类特殊的线性系统，其状态空间矩阵是时变参数向量的函数，时变参数体现了系统的非线性和时变性。LPV控制理论是一种保证系统稳定性和动态性能的变增益技术，是时不变系统控制理论在LPV系统上的推广[9]。利用LPV系统设计控制器有以下几个优点：设计控制器时无需再考虑如何插值；利用时变参数的测量值来提高控制性能；由于设计过程可以通过直接的方式处理参数集，故能从理论上保障系统的鲁棒稳定性以及其他性能要求。

目前，LPV系统的鲁棒变增益控制的研究和应用范围十分广泛，如导弹[10-11]、无人机[12]等，但是，将LPV系统引入航天器姿态控制领域处理容错问题的成果不是很多。文献[13]针对卫星执行机构发生乘性故障，将失效因子作为时变参数并进行具有重叠特性的区间划分，最终建立姿态动力学切换LPV系统。对每一个子系统设计相应的变增益子控制器，控制器增益以及子系统间的切换律均与时变参数有关。而本文考虑转动惯量随时间变化并将转动惯量作为时变参数，将失效因子作为已知上下界且未知的不确定时变参数，最终建立航天器姿态动力学的仿射参数依赖不确定LPV模型。基于LPV模型设计控制器时，为保证不确定系统的鲁棒性引入了保性能控制，为降低控制算法的保守性利用了仿射二次稳定的方法。在航天器姿态控制系统中进行仿真，结果表明控制算法的有效性。

1 航天器执行机构故障的姿态动力学LPV模型

1.1航天器姿态动力学系统模型

因卫星所处环境复杂，燃料消耗，结构改变，温度变化，辐射等均会使卫星的转动惯量发生改变，可靠有效的姿态控制需要考虑航天器转动惯量变化。因此，本文在建立航天器姿态动力学模型时，假设转动惯量随时间变化。

工程上常用的姿态描述法是欧拉角。在欧拉角姿态表示法中，最常用的是按zxy顺序，相应的转角依次记为ψ、φ、ξ分别称为滚动角、俯仰角和偏航角。忽略转动惯量矩阵Ib中的惯量积，姿态动力学方程可以写成

(1)

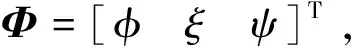
(2)

式中：

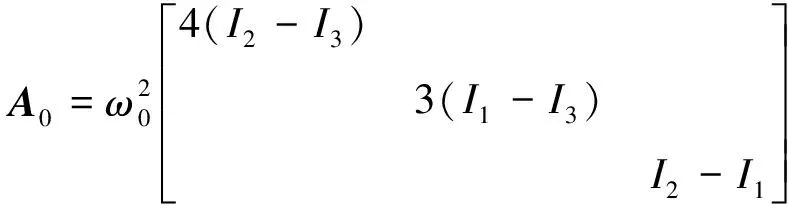
A2=Ib，Gu=E3，En为n维单位矩阵。

(3)

1.2航天器姿态动力学LPV模型

对于LPV系统

(4)

当A(θ)和B(θ)具有如下仿射参数依赖形式时，系统(4)便是仿射参数依赖LPV模型。

(5)

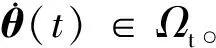
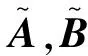
(6)

(7)

式中:θik∈[0,1]，Aik,Bik的表达式如下

(8)

(9)

令θik在整个控制过程中的变化范围是

(10)

则

(11)

故

(12)

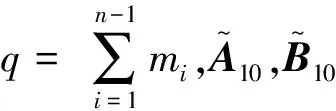
注1. 由式(12)得到的LPV系统，时变参数的变化范围是θik∈[0,1]，将式(12)经过简单的变换便可以得到时变参数在任何范围内变化的LPV系统。

1.3航天器执行机构故障的姿态动力学LPV模型

执行机构的乘性故障是指输出与输入有一定倍数关系，可以表示为

uf=Gu

(13)

式中:u∈Rm为控制矢量，G表示故障对执行机构的影响，为

G=diag(g1,g2,…,gm),gi∈[0,1]

(14)

式中:gi为乘性故障失效因子，当gi=1时执行机构正常运行，gi=0时执行机构完全失效。

考虑航天器姿态控制中，执行机构采用三个正交安装的反作用飞轮，则

G=diag(g1,g2,g3)=g1e11+g2e22+g3e33

(15)

将式(13)、式(15)、式(12)代入式(3)，得到执行机构发生乘性故障时的LPV模型，即

(16)

(17)

(18)

2 鲁棒变增益PID容错控制

2.1问题的描述

引入鲁棒变增益PID控制器:

(19)

KP,KI,KD可表示为仿射参数依赖的形式，即

(20)

(21)

(22)

(23)

引入仿射参数依赖Lyapunov函数

(24)

(25)

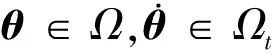
(26)

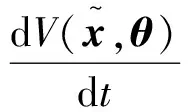
(27)

成立，则闭环系统(21)是仿射二次稳定的。

对系统(3)为了保证保性能性，定义二次性能指标

(28)

式中:Q=QT≥0,Rgt;0,S=ST≥0。

定义2. 对系统(16)和性能指标(28)，如果存在一个控制律u*(t) 和一个正数J*，使得对所有允许的情况，闭环系统是渐近稳定的，且闭环性能指标满足J≤J*，则J*称为系统(16)的一个性能上界，u*(t)称为系统(16)的一个保性能控制器。

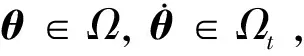
2.2鲁棒变增益PID容错控制的设计

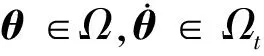
(29)

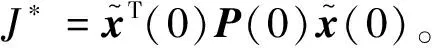
(30)

(31)

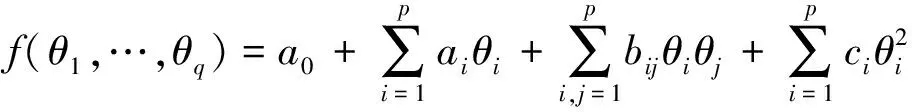
在研究鲁棒变增益PID容错控制的过程中，受到了文献[14-15]的启发，完成了相应容错控制器的设计。

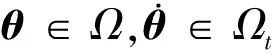
(32)

证. 引入辅助矩阵N1,N2，由式(21)和式(22)得

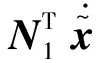
(33)

式(27)可以写为

(34)

同时

(35)

(36)

注2. 鲁棒变增益PID容错控制的设计，最终转化为双线性矩阵不等式组可行解的问题，故本文利用了Tomlab优化工具箱中的PenBMI求解器。

注3. 令Fi=0,Fdi=0，根据定理1所求得的控制u(t)就是保证闭环系统仿射二次稳定的保性能PID容错控制器。即传统的PID容错控制是一种特殊的鲁棒变增益PID容错控制。

3 仿真校验

仿真中，假定航天器初始时的转动惯量为I0=diag(200,100,300) kg·m2，在10≤t≤110 s匀速改变到If=diag(120,150,90) kg·m2，如图1所示。

求解控制器时，令n=2，m1=1，根据式(8)、式(9)、式(12)，引入一个时变参数θ1∈[-1,1]，如图2所示。对于在轨运行的航天器而言，主要控制的目标为尽量减少燃料消耗[14,16]，因而选取的Q、S、和R为Q=0.1E6,R=E3,S=0.001E6。令gi∈[0.3,1],i=1,2,3，根据式(16)和定理1，本文分别求解了使闭环系统仿射二次稳定的保性能PID容错控制器和鲁棒变增益PID容错控制器。本文所采用的航天器仿真参数见表1。

(1) PID容错控制

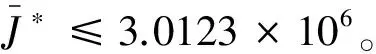
表1 航天器姿态仿真参数Table 1 Simulation parameters of spacecraft attitude control

图3是飞轮无故障、在初始时刻发生故障1、故障2、故障3时，PID容错控制的仿真图像。可知，4种情况系统均在200 s附近达到稳定，飞轮在无故障以及发生乘性故障的情况下，闭环系统的稳定性能相近，即PID容错控制是有效的。

(2)鲁棒变增益PID容错控制

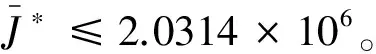
图4是飞轮无故障、在初始时刻发生故障1、故障2、故障3时，鲁棒变增益PID容错控制的仿真图像。可知，在4种情况下，闭环系统均在150 s附近达到稳定，闭环系统的稳定性能相近，即鲁棒变增益PID容错控制是有效的。

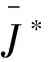
图5是以偏航轴为例，系统达到稳定后无故障、故障1、故障3时仿真对比图像。由图5可知，几种情况下均能达到较高的控制精度，但是随着故障程度的增加，控制精度略有降低。

PID容错控制是一种特殊的鲁棒变增益PID容错控制，相当于KPi=KIi=KDi=0，即PID容错控制的参数是固定不变的，不随时变系统的变化而改变，因此，对于时变系统而言，PID容错控制的设计，增大了保守性，一定程度上牺牲了系统的性能。而鲁棒变增益PID容错控制通过引入时变参数，降低了控制过程中的保守性，改善了系统的性能。另一方面，鲁棒变增益容错控制最终转化为双线性矩阵不等式可行解的问题，故一定程度上增大了计算量。

4 结 论

对于航天器执行机构乘性故障的姿态容错控制，本文考虑转动惯量随时间改变，将转动惯量信息作为实时可测的时变参数，失效因子作为不确定的时变参数，建立姿态动力学的仿射参数依赖不确定LPV系统。鲁棒变增益容错控制的设计，利用仿射二次稳定的方法降低算法的保守性和引入保性能控制保证不确定系统具有一定的鲁棒性。仿真结果表明控制器是有效的。与PID容错控制相比，鲁棒变增益PID容错控制器与时变参数有关，一定程度上改善了系统的性能。然而，变增益PID容错控制最终转化为双线性矩阵不等式可行解的问题，增加了控制器求解的复杂度。

[1] Tafazoli M. A study of on-orbit spacecraft failures[J]. Acta Astronautica, 2009, 64(2): 195-205.

[2] 贾庆贤, 张迎春, 陈雪芹, 等. 卫星姿态控制系统故障重构观测器设计[J]. 宇航学报, 2016, 37(4): 442-450.[Jia Qing-xian, Zhang Ying-chun, Chen Xue-qin, et al. Observer design for fault reconstruction in satellite attitude control system[J]. Journal of Astronautics, 2016, 37(4): 442-450.]

[3] Zhang A, Hu Q, Zhang Y. Observer-based attitude control for satellite under actuator fault[J]. Journal of Guidance, Control, and Dynamics, 2014, 38(4): 806-811.

[4] Li D, Lei J. Fault-tolerant attitude control of spacecraft by using robust adaptive method[C]. IEEE International Conference on Electronic Measurement amp; Instruments, Qingdao, China, July 16-18, 2015.

[5] Zhou Z, Gao Z, Xu Y, et al. Fault tolerant attitude control design for rigid satellite using sliding mode observer technique[C]. IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, August 12-14, 2016.

[6] Jiang Y, Hu Q, Ma G. Adaptive back stepping fault-tolerant control for flexible spacecraft with unknown bounded disturbances and actuator failures[J]. ISA Transactions, 2010, 49(1): 57-69.

[7] Xiao B, Hu Q, Zhang Y, et al. Fault-tolerant tracking control of spacecraft with attitude-only measurement under actuator failures[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 838-849.

[8] 管宇. 卫星姿态控制系统的故障诊断与容错方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.[Guan Yu. Research on fault diagnosis and fault-tolerant control of satellite attitude control system[D]. Harbin: Harbin Institute of Technology, 2012.]

[9] 袁士春. 船舶运动与主推进线性变参数联合控制的研究[D]. 大连: 大连海事大学, 2007.[Yuan Shi-chun. Integrated control of ship motion and main engine propulsion based on linear parameter-varying[D]. Dalian: Dalian Maritime University, 2007.]

[10] Mehrabian A R, Roshanian J. Design of gain-scheduled autopilot for a highly-agile missile[C]. International Symposium on Systems and Control in Aerospace and Astronautics, Harbin, China, January 19-21, 2006.

[11] Yu J, Li L, Zhao H, et al.Robust gain-scheduled controller design for air defense missile[C]. Chinese Control Conference, Harbin, China, August 7-11, 2006.

[12] Natesan K, Gu D W, Postlethwaite I, et al. Design of flight controllers based on simplified LPV model of a UAV[C]. IEEE Conference on Decision and Control, San Diego, CA, USA, December 13-15, 2006.

[13] He X, Zhang W,Leng Y, et al. Fault tolerant control with switched LPV method based on hysteresis strategy and an application to a microsatellite model[C]. The 34th Chinese. IEEE Control Conference, Hangzhou, China, July 28-30, 2015.

[14] Vesely V, Ilka A. Gain-scheduled PID controller design[J]. Journal of Process Control, 2013, 23(8): 1141-1148.

[15] Vesely V, Ilka A. Robust gain-scheduled PID controller design for uncertain LPV systems[J]. Journal of Electrical Engineering, 2015, 66(1): 19-25.

[16] 马清亮, 杨海燕, 岳瑞华, 等. 空间飞行器大角度姿态机动最优保性能控制[J]. 空间控制技术与应用, 2013, 39(3): 8-13.[Ma Qing-liang, Yang Hai-yan, Yue Rui-hua, et al. Optimization control of spacecraft large angle attitude maneuvers[J]. Aerospace Control and Application, 2013, 39(3): 8-13.]

SpacecraftAttitudeFaultTolerantControlwithActuatorFault

GENG Yun-hai, JIN Rong-yu, CHEN Xue-qin, LI Dong-bai

(Research Center of Satellite Technology, Harbin Institute of Technology, Harbin 150001，China)

For spacecraft attitude control with actuator (flywheel) fault, robust gain-scheduled PID fault tolerant control is designed based on linear parameter varying (LPV) system. Considering the inertia changing and actuator multiplicative fault, the spacecraft attitude dynamics can be rewritten as an uncertain LPV system. The conservation of the controller algorithm is reduced by affine quadratic stability and the robust performance is ensured by guaranteed cost control. The simulation results show the effectiveness of the controller.

Spacecraft attitude control; Fault tolerant control; Actuator fault; Linear parameter varying (LPV); Robust gain-scheduled control

V448.2

A

1000-1328(2017)11- 1186- 09

10.3873/j.issn.1000- 1328.2017.11.007

2017- 07- 03;

2017- 09- 14

微小型航天器技术国防重点学科实验室开放基金(HIT.KLOP.MST.201603); 国家重点研发计划(2016YFB0500901)

耿云海(1970-)，男，博士，教授，主要从事航天器姿态动力学与控制研究。

通信地址：哈尔滨工业大学卫星技术研究所(150001)

电话：18645115250

E-mail：gengyh@hit.edu.cn

陈雪芹(1982-)，女，副研究员，主要从事航天器姿态控制研究。本文通信作者。

通信地址：哈尔滨工业大学卫星技术研究所(150001)

电话：18500218686

E-mail：cxqhit@163.com