一种基于GPS/INS全组合的航向自适应滤波算法

田 源，隋立芬，田翌君，肖国锐，戴 卿

(信息工程大学地理空间信息学院，郑州 450001)

一种基于GPS/INS全组合的航向自适应滤波算法

田 源，隋立芬，田翌君，肖国锐，戴 卿

(信息工程大学地理空间信息学院，郑州 450001)

首先基于陆地导航讨论了GPS/INS全组合系统，分别在载体动态和静态两种情况下对比分析了全组合和紧组合的姿态矫正效果。实验结果表明全组合模式的航向角精度较紧组合有明显提升，且当载体由动态转为静态时，全组合模式能够克服紧组合航向角缓慢发散的现象。其次针对载体大角度转向时组合系统动力学模型异常增大的问题，提出了一种对航向角进行自适应修正的全组合滤波算法，仿真实验结果表明：该方法能够一定程度上削弱载体大角度转向时动力学模型异常的影响，航向精度有一定提高。

GPS/INS组合；全组合系统；航向角；自适应滤波；分类因子

0 引 言

惯性导航系统(Inertial navigation system, INS)作为独立自主高动态的导航系统，与GNSS有着良好的互补性，二者组合系统在车辆导航、移动测图系统、航空摄影测量等高精度定位领域得到广泛应用[1]。随着GNSS姿态测量技术的发展，GNSS多天线测姿已具备实时姿态获取的能力[2-3]，因此可以将姿态信息加入GNSS/INS组合滤波器与位置速度一起进行数据融合。该方法能克服传统组合方式中姿态误差及INS元件误差需要根据位置和速度等误差之间的关系来估计的缺陷，提高组合系统的导航精度[4]。

本文将加入姿态信息之后的组合系统分为不完全组合和完全组合两种形式。不完全组合即仅利用三个姿态角的其中之一进行组合。由于在陆地导航中俯仰角和横滚角一般数值较小影响较弱，单独与INS组合效果不大，因此该方面的研究通常只采用航向角组合。其中吴富梅、柴艳菊等多位学者提出利用GPS单天线确定的航向角与INS航向角组合[5-7]，提高了组合系统姿态误差和元件误差的估计精度且系统成本较低。但GPS单天线得到的姿态角由速度或位置增量导出，被称为伪姿态，这种计算方法也决定了GPS单天线测姿在载体低速或静止状态时精度很差的特点[8]。完全组合即为全组合系统，多采用GPS多天线姿态测量值进行组合。该方式中姿态参数由间接估计转变为直接估计，在GPS姿态测量值精度能够保证的情况下，组合系统姿态参数估值的准确性能够得到一定提高[9-11]。多天线姿态较单天线得到的伪姿态更加稳定，因此在载体低速或静止情况下全组合系统理论上能够同样保持较高精度的姿态输出，但目前鲜有研究对该情况做出详细分析。

在低成本陆地导航中，全组合系统虽能够提高姿态精度，但依然无法克服GPS/INS组合在载体大角度转向时状态异常增大导致航向精度变差的问题。原因是低成本陆地导航采用低成本设备，且系统模型具有不确定性，包括模型状态简化，噪声及初始状态统计特性建模不准确等[12]。因此载体在转向时，随着航向角变化幅度的增大动力学模型误差增大，标准Kalman滤波不能控制动力学模型异常扰动的影响从而导致滤波精度较低[13]。本文在GPS/INS紧组合的基础上扩充姿态观测方程，以“伪距伪距率紧组合+姿态松组合”的策略构成全组合系统，在载体动态和静态两种情况下分析其姿态校正效果。并引入自适应滤波理论[14]，以期削弱载体大角度转向时动力学模型异常扰动的影响，最后通过实验对采用自适应滤波前后的航向角结果进行了对比分析。

1 GPS/INS全组合滤波模型

1.1状态方程

GPS/INS全组合系统是一个连续的过程，与紧组合系统的区别在于量测方程的扩充，状态方程与紧组合一致，可用连续微分方程的形式描述：

(1)

其中，X(t)为系统状态，F(t)和G(t)为系数阵，u(t)为驱动白噪声过程。

将(1)式离散化，得离散的状态方程：

Xk=Φk,k-1Xk-1+GkWk

(2)

其中，Φk,k-1为离散后的状态转移矩阵；Wk为动力学模型噪声；Gk为模型噪声分配阵；Xk-1，Xk分别为k-1和k历元的状态参数向量，取如下所示的20维状态参数：

X=[δPδVφεbεr▽δtδtr]T

(3)

从前到后分别为位置、速度误差，平台失准角(计算得到的姿态矩阵和真实姿态矩阵之间的旋转角度误差)，陀螺仪常值零偏、相关漂移，以及加速度计偏置和接收机钟差、钟速。

1.2加入姿态的观测方程扩充

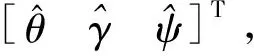
(4)

(5)

其中，C和S为余弦和正弦算子。该姿态矩阵与真实姿态矩阵R之间的存在如下关系：

(6)

其中，旋转矩阵R′可表示为[15-16]：

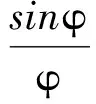
(7)

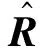
(8)

对式(7)进行近似处理，由于等效旋转角度φ为小量，故sinφ/φ≈1，并忽略式中的二阶小量，则式(6)变为：

(9)

将式(4)代入式(9)，可推出平台失准角和姿态角误差之间的关系：

(10)

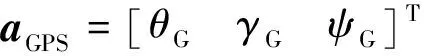
aINS-aGPS=Aa,3×3·φ+εA

(11)

(12)

其中,φ表示失准角；εA表示角度量测噪声。将式(11)扩充到GPS/INS紧组合观测方程中，即得到全组合系统观测方程：

(13)

(14)

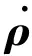
2 自适应卡尔曼滤波

GPS/INS组合系统是一个非线性连续系统，常采用扩展卡尔曼滤波(Extended Kalman filter, EKF) 作为数据融合工具。联立式(2)和式(13)，利用扩展卡尔曼滤波就能得到每一历元的状态参数滤波解，现为了削弱大角度转向时动力学模型异常扰动的影响，减小航向角误差，引入自适应滤波理论并直接给出自适应滤波解：

(15)

(16)

其中,ΔMk表示状态异常判别量；c为经验常数，通常取c=1.0～1.5。

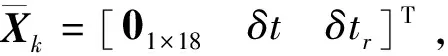
本文提出一种基于闭环校正的自适应滤波策略，仅对航向角进行自适应修正。新息向量计算式如下：

(17)

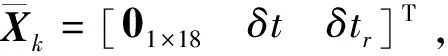
(18)

由式(18)可知,对于闭环校正新息与观测等价。此时在GPS姿态测量值可靠的情况下，组合系统的航向观测值(INS航向角与GPS航向角之差)能够部分反映出系统的状态异常。因此可借鉴分类因子自适应滤波[18-19]的思想，直接利用组合系统的航向观测值单独构造自适应因子对航向角进行自适应修正。航向观测值即以GPS的航向角为真值时的INS航向角误差Δψ，状态异常判别量可按下式构造：

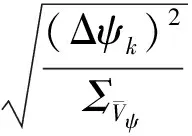
(19)

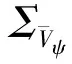
(20)

其中，αyaw为航向角自适应因子；I为单位阵。

3 实验分析

设计了两组仿真实验。实验一分析了全组合系统在载体动态和静态两种状态下的解算效果。实验二分析了航向自适应修正算法的效果。在两组实测的车载组合导航数据的基础上仿真GPS姿态测量值进行实验。

数据一：动态数据，INS陀螺零偏为1.0°/h；加速度计偏置为10-4g；采样率为100 Hz；GPS采样频率为10 Hz；组合周期为1 s；伪距观测中误差取4 m；伪距率观测中误差取0.06 m/s。将陀螺仪与高精度的GPS RTK组合得到的姿态角作为参考值。在姿态参考值上加入标准差为0.2°的伪随机噪声作为GPS姿态测量值。

数据二：包含一段静止状态，INS陀螺零偏1.0°/h；采样频率100 Hz；GPS采样率1 Hz；组合周期1 s；伪距观测中误差取3 m；伪距率观测中误差取0.06 m/s。以高精度导航级惯导构成的组合定位定姿系统POS LV610输出的姿态作为参考真值。在姿态参考值上加入标准差为0.2°的伪随机噪声作为GPS姿态测量值。

3.1实验一

分别按照两种方案对上述两组数据进行组合导航解算：

方案一：紧组合模式(Tightly integrated, TI)；

方案二：全组合模式(Completely integrated, CI)。

首先给出数据一两种方案的解算结果。图1表示航向角误差；图2表示方案二的航向角结果；表1给出了数据一的姿态误差统计。

表1 数据一的姿态角RMSTable 1 Attitude RMS of data 1

从以上结果可以看出：

1)图1的航向角误差对比清楚的表明了全组合的优势。相比于紧组合而言，全组合的误差曲线更加集中，航向角精度提升非常明显。由表1可知,提升幅度大约为60%。本文对航向角的定义为：(-180°,180°)，因此图2中在500历元左右线条出现的跳变是正常现象。将图1和图2进行对比分析可以看出，在航向角数值出现较大变化的历元，两种方案的航向误差曲线因为状态异常的变大而存在一些相对较大波动，紧组合受影响程度更大。图1中1000历元之后包含一小段静止状态，可看出紧组合航向误差呈缓慢发散趋势。

2)由表1可知，全组合解算的横滚角的RMS小于紧组合结果，说明全组合解算横滚角精度更高，而俯仰角精度较紧组合有秒级别的微略降低。由于低成本车载导航中通常只考虑航向角，且俯仰角和横滚角数值通常较小，所以俯仰角精度的略微损失这里可忽略不计。

以上为动态情况下的结果分析，下面给出数据二的解算结果。由于依然为车载数据，俯仰角和横滚角结果与数据一结果类似，因此只给出航向角结果，如图3和图4所示。

表2 数据二航向角RMSTable 2 The yaw’s RMS of data 2

图4中，120历元左右载体有一个大角度的转向，图3相应历元的航向角误差也出现了较大波动，较图1更明显地说明全组合在大角度转向时航向精度会变差。在280历元左右载体由动态变为静止状态，紧组合解算的航向角误差存在逐渐发散的现象，原因是静止状态下航向角误差可观测性不高，且间接估计姿态参数不够准确。全组合利用外部姿态观测值直接估计失准角，航向角误差可观测性好，在静止状态下能够较好的估计航向角误差，因此航向角误差不存在发散现象。由表2可知，全组合的航向角精度较紧组合有很大提升。

3.2实验二

分别用数据一和数据二验证自适应算法，自适应滤波阈值c取值1.5，用以下两种方案解算：

方案一：普通的全组合(CI)；

方案二：航向自适应修正的全组合(ACI)。

本实验算法主要针对在载体大角度转向时航向角精度差的问题，因此只给出航向角结果图，如图5和图7所示，图6和图8展示了航向角自适应判别量ΔMk的取值与判定阈值c的关系；两组数据姿态解算结果的误差统计见表3。

表3 实验二的航向角RMSTable 3 The yaw’s RMS of test 2

由图5和图7可以看出，ACI方案误差曲线较CI方案改善许多；由图7可以明显地看出航向精度跳变时ACI方案具备较好的修正效果；如表3所示，两组数据ACI方案的航向RMS较CI方案明显降低，数据一提升约13%，数据二提升约50%。说明在航向精度变差的时候ACI方案一定程度上能够削弱状态异常的影响，从而使得航向精度有所提高。

4 结束语

本文主要对全组合系统的姿态解算进行了分析研究。全组合模式的姿态精度优于紧组合模式，其中航向角精度提升非常明显，俯仰角和横滚角由于在车载实验中数值较小的缘故，精度仅有略微变化。在载体由动态转变为静止状态的情况下，由于紧组合模式航向误差可观测性差的缘故，航向角结果存在缓慢发散的现象，而加入了外部姿态观测的全组合模式能够很好的克服该问题。但全组合系统依然无法克服载体大角度机动时由于动力学模型异常变大而导致的航向精度变差这一现象。针对该问题，本文提出的闭环修正模式下单独构造航向角自适应因子的自适应滤波算法能够一定程度上削弱动力学模型异常的影响，航向精度有一定提高。

[1] Grejner-Brzezinska D A, Da R, Toth C. GPS error modeling and OTF ambiguity resolution for high-accuracy GPS/INS integrated system [J]. Journal of Geodesy, 1998, 72(11): 626-638.

[2] 王冰. 基于GNSS的实时姿态确定算法研究[D]. 郑州：解放军信息工程大学, 2013. [Wang Bing. Research on real-time attitude determination algorithms utilizing global navigation satellite system [D]. Zhengzhou:PLA Information Engineering University. 2013.]

[3] Zhao L, Li N, Li L, et al. Real-time GNSS-based attitude determination in the measurement domain [J]. Sensors, 2017, 17(2):296.

[4] 马宏阳, 程鹏飞, 黄华东. GPS/INS位置、速度和姿态全组合导航系统研究[J]. 测绘通报, 2016(3):10-14. [Ma Hong-yang, Cheng Peng-fei, Huang Hua-dong. Research on the complete integrated GPS/INS navigation system of position, velocity and attitude [J]. Bulletin of Surveying and Mapping, 2016(3):10-14.]

[5] 吴富梅, 聂建亮, 何正斌. 低成本车载GPS/INS组合导航姿态角更新算法[J]. 中国惯性技术学报, 2010, 18(6):675-679. [Wu Fu-mei, Nie Jian-liang, He Zheng-bin. Low-cost GPS/INS integrated navigation algorithm in land vehicle system considering attitude update [J]. Journal of Chinese Inertial Technology, 2010, 18(6):675-679.]

[6] 柴艳菊, 欧吉坤, 袁运斌,等. 附加方位约束的GPS/INS组合系统选权自适应卡尔曼滤波[J]. 测绘学报, 2011, 40(4):421-428. [Chai Yan-ju, Ou Ji-kun, Yuan Yun-bin, et al. The adaptive Kalman filtering for single antenna GPS/INS integrated system with heading angle constraint by selecting the parameter weights [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4):421-428.]

[7] Li Y, Efatmaneshnik M, Dempster A G. Attitude determination by integration of MEMS inertial sensors and GPS for autonomous agriculture applications [J]. GPS Solutions, 2012, 16(1):41-52.

[8] 甘雨, 隋立芬, 戚国宾,等. 陆地导航中GNSS/陀螺仪组合实时测姿方法[J]. 武汉大学学报信息科学版, 2015, 40(3):379-383. [Gan Yu, Sui Li-fen, Qi Guo-bin, et al. A real-time attitude determination approach for land navigation based on GPS/Gyroscope integration [J]. Geomatics and Information Science of Wuhan University, 2015, 40(3):379-383.]

[9] 赵伟, 袁信, 林雪原. 基于H ∞滤波技术的GPS/INS全组合导航系统研究[J]. 宇航学报, 2002, 23(3):39-43. [Zhao Wei, Yuan Xin, Lin Xue-yuan. Research on GPS/INS integration based on H∞ filter [J]. Journal of Astronautics, 2002, 23(3):39-43.]

[10] 杨艳娟, 卞鸿巍, 田蔚风,等. 一种新的INS/GPS组合导航技术[J]. 中国惯性技术学报, 2004, 12(2):23-26. [Yang Yan-juan, Bian Hong-wei, Tian Wei-feng, et al. A new INS/GPS integrated navigation technique [J]. Journal of Chinese Inertial Technology, 2004, 12(2):23-26.]

[11] 周姜滨, 袁建平, 罗建军,等. 基于联邦滤波的SINS/GPS全组合导航系统研究[J]. 系统仿真学报, 2009, 21(6):1562-1564. [Zhou Jiang-bin, Yuan Jian-ping, Luo Jian-jun, et al. Fully integrated SINS/GPS navigation system based on federated filters [J]. Journal of System Simulation, 2009, 21(6):1562-1564.]

[12] 王小旭, 赵琳. 自适应融合滤波算法及其在INS/GPS组合导航中的应用[J]. 宇航学报, 2010, 31(11):2503-2511. [Wang Xiao-xu, Zhao Lin. Adaptive fusion filtering algorithm and its application for INS/GPS integrated navigation system [J]. Journal of Astronautics, 2010, 31(11):2503-2511.]

[13] 吴富梅, 聂建亮, 何正斌. 利用预测残差和选权滤波构造的分类因子在GPS/INS组合导航中的应用[J]. 武汉大学学报(信息科学版), 2012, 37(3):261-264. [Wu Fu-mei, Nie Jian-liang, He Zheng-bin. Classified adaptive filtering to GPS/INS integrated navigation based on predicted residuals and selecting weight filtering [J]. Geomatics and Information Science of Wuhan University, 2012, 37(3):261-264.]

[14] 杨元喜, 何海波, 徐天河. 论动态自适应滤波[J]. 测绘学报，2001, 30(4):293-298. [Yang Yuan-xi, He Hai-bo, Xu Tian-he. Adaptive robust filtering for kinematic GPS positioning [J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4):293-298 .]

[15] Markley F. Attitude error representations for Kalman filtering [J]. Journal of Guidance, Control and Dynamics，2003, 26(2):311-317.

[16] 高钟毓. 惯性导航系统技术[M]. 北京：清华大学出版社，2012.

[17] 秦永元，张洪钺，汪叔华. 卡尔曼滤波与组合导航原理(第二版)[M]. 西安：西北工业大学出版社，2012.

[18] 崔先强, 杨元喜. 分类因子自适应抗差滤波[J]. 自然科学进展, 2006, 16(4):490-494. [Cui Xian-qiang, Yang Yuan-xi. Adaptively robust filtering with classified adaptive factors [J]. Progress in Natural Science, 2006, 16(4):490-494.]

[19] Yang Y X, Cui X Q. Adaptively robust filter with multi adaptive factors [J]. Survey Review, 2008, 40(309):260- 270.

AnAdaptiveFilteringAlgorithmforYawBasedonGPS/INSCompletelyIntegratedSystem

TIAN Yuan, SUI Li-fen, TIAN Yi-jun, XIAO Guo-rui, DAI Qing

(Institute of Geospatial and Information, Information Engineering University, Zhengzhou 450001, China)

Firstly, the GPS/INS completely integrated system is discussed based on land navigation. The attitude correction effects of the completely-integrated and tightly-integrated are respectively analyzed under the kinematic state and static state. The test result is concluded that the yaw precision of the completely-integrated is obviously better than that of the tightly-integrated. And the situation of the yaw’s slow divergence, appearing in the tightly-integrated when the carrier transforms from the kinematic state to static state, can be overcome by the completely-integrated. Secondly, in view of the situation that the anomaly of the kinetic model increases when the carrier is under large-angle turning, a completely-integrated filtering algorithm which only adaptively modifies the yaw is introduced. The simulated test result shows that the influence of the dynamic model abnormity enlarged during large-angle turning can be partly weakened and the yaw precision is partly improved.

GPS/INS integrated; completely integrated system; yaw; adaptive filtering; classified adaptive factor

P228.4

A

1000-1328(2017)11- 1212- 07

10.3873/j.issn.1000- 1328.2017.11.010

2017- 06- 16;

2017- 08- 29

国家自然科学基金(41674016,41274016)

田源(1993-)，男，硕士生，主要从事GNSS/INS组合定位测姿的研究。

通信地址：河南省郑州市高新区科学大道62号(450001)

电话:18790272987

E-mail：tyuan1247@qq.com.

隋立芬(1961-)，女，教授,主要从事测量数据处理理论与方法的研究。本文通信作者。

通信地址：河南省郑州市高新区科学大道62号(450001)

E-mail：suilifen@163.com