带支撑Maxwell阻尼器多层隔震结构的随机地震响应分析

邹万杰， 马 媛， 李创第， 葛新广

(广西科技大学 土木建筑工程学院， 广西 柳州 545006)

带支撑Maxwell阻尼器多层隔震结构的随机地震响应分析

邹万杰， 马 媛， 李创第， 葛新广

(广西科技大学 土木建筑工程学院， 广西 柳州 545006)

对隔震层附设带支撑的五参数Maxwell阻尼器的多层基础隔震结构随机地震响应解析解法及平稳响应进行了研究。首先将上部结构用第一振型展开，采用带支撑的五参数Maxwell阻尼器的积分型分析模型，用微分积分方程组实现对该结构的时域非扩阶精确建模；然后采用传递矩阵法，直接在耗能隔震结构原空间获得结构在任意激励下的位移、速度和阻尼器的时域瞬态响应解析表达式；最后在Kanai-Tajimi平稳滤过白噪声激励下，基于该解析解，获得了结构的位移、速度和阻尼器受力的随机响应方差，并给出算例，从而建立了该多层隔震结构在Kanai-Tajimi滤过白噪声激励下的随机响应解析分析方法。

五参数Maxwell阻尼器； 支撑； 多层隔震结构； 传递矩阵法； 阻尼器受力

隔震结构是在建筑物上部结构与基础之间设置滑移层、橡胶隔震支座等，阻止地震能量向上传递[1]。目前，国内外应用最广泛的隔震技术是在基础采用橡胶支座隔震系统[2]。在耗能隔震结构体系中，阻尼器充分发挥耗能作用，消耗了输入到结构中的大部分地震能量，能够有效地保护结构主体，使其免受破坏，即，结构的反应会减小。因此，阻尼器的受力日益受到关注；为确保主体结构的安全，将通过求解与分析阻尼器的受力，来确定结构响应的合理性。

黏弹性阻尼器是一种有效的被动减振控制装置[3]。Maxwell阻尼模型本构方程简单，易于扩阶，计算参数便于试验数据的拟合[4-5]。黏弹性阻尼器的力学模型可用Maxwell模型[6-11]或五参数Maxwell模型[12-14]来近似表示。

在试验及大量数值计算的基础上，我国抗震规范通过限制最小支撑刚度来保证支撑与阻尼器串联的复合阻尼元件发挥或接近纯阻尼元件的效果[15]。为提高精度，有必要考虑有限支撑刚度的影响[16-17]。

黏弹性阻尼结构的现有解析法有扩阶精确法和非扩阶近似法。扩阶精确法的不足在于扩阶方程组的物理意义不明确，变量个数剧增，计算效率低；非扩阶近似法有模态应变能法[18]以及随机平均法，由于采用较多近似假设，其精度及适用范围有待提高。

考虑到传递矩阵法[19]无需扩阶，可直接获得一般黏滞阻尼对称线性定常结构的脉冲响应矩阵的精确解[20-21]。故本文对带支撑的五参数Maxwell阻尼隔震结构进行非扩阶微分积分方程进行建模，选择传递矩阵法，获得该耗能隔震结构在任意激励下的非扩阶时域瞬态响应解析解和基于Kanai-Tajimi滤过白噪声激励的随机响应解析解。

1 运动方程

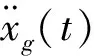
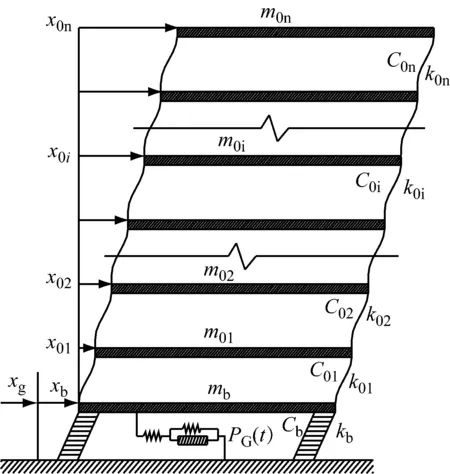
图1 结构计算简图

(1)

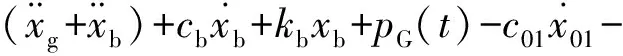
k01x01=0

(2)

(3)

式中：I0=[1，1，…，1]T，hG(t)为带支撑修正阻尼器的松弛函数。

图2 隔震层阻尼器计算简图

在被动隔震工程中，上部多层结构一般为经典结构，可将位移向量x0按上部多层结构第一振型φ1=[φ11,φ12,…,φ1n]T及其对应的广义坐标x1(t)展开，即：

x0=φ1x1(t)

(4)

令：

(5)

式中：ξ1、ω1分别为上部结构第一振型的阻尼比和频率；、αiβi为比例系数，i=1～n。则方程式(1)～(3)可化为带有积分的非对称动力方程：

(6)

式中：

(7)

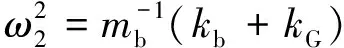
(8)

(9)

式中：kG为修正后阻尼器的平衡模量；kQ为原阻尼器的平衡模量；kp为支撑刚度；x1为按第一阶振型展开后的广义位移；xb为隔震层位移；ξ2、ω2分别为隔震层的阻尼比和频率。

2 结构瞬态响应的传递矩阵法

2.1结构特征值分析

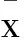
(10)

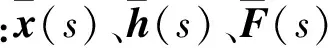
令：

(11)

对式(11)取拉氏变换得：

(12)

由式(10)，得：

(13)

(14)

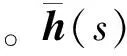
(15)

其中，原阻尼器hQ(t)的拉氏变换为：

(16)

通过结构的特征方程式(17)可求出结构的Ne个特征值sj，其中有2对共轭复特征值和w个负实特征值，w与修正阻尼器松弛函数hG(t)的拉氏变换式有关。

(17)

每个sj对应的右、左特征向量uj、vj可由式(18)求出：

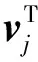
(18)

2.2传递矩阵解析表达式

式(17)求出的特征值sj是传递矩阵H(s)的极点，可将H(s)按其极点sj的残数矩阵展开[22]，即：

(19)

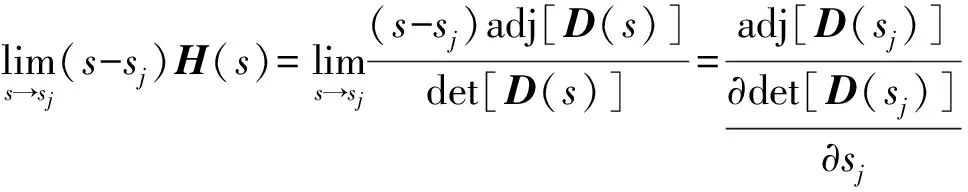
(20)

式中：adj[D(s)]为D(s)的伴随矩阵。

根据式(17)，有：

D(sj)adj[D(sj)]=adj[D(sj)]D(sj)=

Idet[D(sj)]=0

(21)

式中：I为单位矩阵。

将式(18)与式(21)比较，可得：

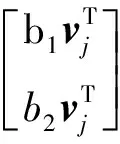
(22)

式中：ak，bk(k=1～2)均为常数。

令：

uj=[u1j,u2j]T

(23)

从式(22)知：伴随矩阵adj[D(s)]的两行元素之比相等，即：

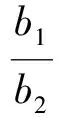
(24)

故有：

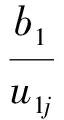
(25)

式中：lj是比例常数；k=1～2。

将式(25)代入式(22)，得：

(26)

将式(26)代入式(20)，得：

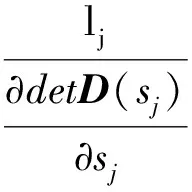
(27)

式中：ηj为常数。

下面求ηj的表达式。由式(19)和(27)，有：

(28)

(29)

且有：

(30)

(31)

式中：θi为常数，i=1～Ne，式(30)的表达式由式(14)得出。

由式(19)和(27)，得H(s)的解析式为：

(32)

式中：常数ηj由式(30)和(31)计算。

由式(19)、(20)，得sH(s)的解析式为：

(i=1～Ne)

(33)

将式(27)代入式(33)，有：

(34)

(35)

(i=1～Ne)

(36)

将式(27)代入式(35)、(36)，有：

(37)

2.3结构位移、速度时域响应解析表达式

由式(13)、(32)、(34)，得：

(38)

(39)

对式(38)、(39)取拉氏逆变换，并根据式(9)，得上部结构广义位移、速度和隔震层位移、速度响应解析表达式：

(40)

(41)

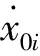
x0i=φ1ix1(t)

(42)

(43)

Δx0i=x0i-x0(i-1)=(φ1i-φ1(i-1))x1(t)

(44)

(45)

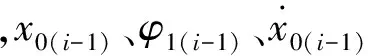
根据式(40)～(45)，隔震层相对地面、上部结构各层相对隔震层的位移、速度及上部结构各层层间位移、速度均可统一表示为：

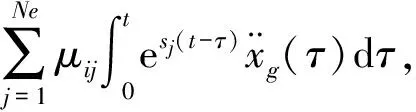
z=1,2,3,4,i=0～n

(46)

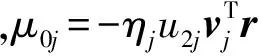
2.4结构阻尼器响应解析表达式

由式子(12)、(13)、(37)得

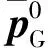
(47)

对式(47)取拉氏逆变换，并根据式(9)，得：

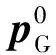
(48)

由式(3)、(7)、(11)知，隔震层修正后的黏弹性阻尼器的响应，为：

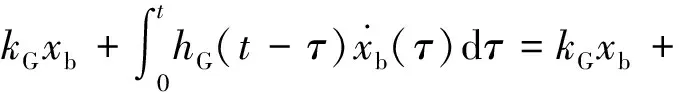
mbp2(t)

(49)

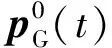
(50)

根据式(46)，将xb(t)表达式和式(50)，代入式(49)，得隔震层阻尼器的响应，为：

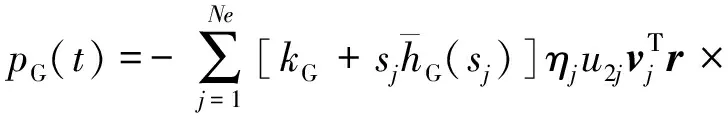
(51)

根据以上求解的结构位移、速度及阻尼器的响应表达式(46)、(51)，可以看出对于一般线性黏弹性阻尼多层隔震结构，其位移、速度、层间位移、层间速度、阻尼器受力响应量S(t)均可统一表示为：

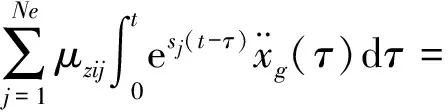
(52)

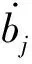
(53)

(54)

3 结构平稳随机响应解析解

3.1经典Kanai-Tajimi过滤白噪声激励

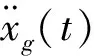
(55)

(56)

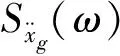
q=-α+jβ

(57)

(58)

(59)

相关参数S0、ωg、ξg的具体取值可参见文献[24]。

3.2结构平稳响应解析解

由式(52)和式(54)，可得平稳地震激励下结构响应协方差表达式：

(60)

(61)

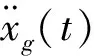
(62)

式中：

(63)γjk=

(64)

将式(62)代入式(60)，得此情况下结构响应Szi(t)的平稳协方差表达式。

4 算 例

某八层基础隔震钢筋混凝土框架结构，上部结构各层质量m01至m08分别为300×103kg、300×103kg、270×103kg、270×103kg、270×103kg、270×103kg、270×103kg、130×103kg；层间刚度k01至k08分别为400×103kN/m、350×103kN/m、350×103kN/m、350×103kN/m、350×103kN/m、350×103kN/m、350×103kN/m、250×103kN/m；仅考虑上部结构第一振型的影响，第一振型为，φ1=[0.174,0.366,0.541,0.695,0.822,0.916,0.973,1.000]T对应的第一频率ω1=7.170 s-1，阻尼比ξ1=0.05。隔震层质量和刚度分别为mb=440×103kg，kb=40×103kN/m，阻尼比取为ξ2=0.20。隔震层附设一带支撑的五参数Maxwell阻尼器，结构计算模型如图1。阻尼器取值为：平衡模量kq=1.00×103kN/m，两分支标准Maxwell阻尼器的刚度都取为：kl=8×103kN/m(l=1,2)，松弛时间的倒数μ1=μ2=10 s-1,支撑刚度kp按照以下五种工况取值0.2kb、0.4kb、0.6kb、0.8kb、kb。在经典Kanai-Tajimi平稳过滤白噪声地震激励下的参数取值为(地震烈度为I=8度)：S0=0.013 87 m2/s3，ωg=16.5 s-1，ξg=0.8。

表1、表2分别给出了该8层隔震耗能结构在支撑刚度取五种不同工况下以及在相同参数下，阻尼器不加支撑和隔震层无阻尼器结构各楼层相对于地面的位移、速度响应方差，相对应的图形如图3、4所示；阻尼器的受力响应方差如表3所示。

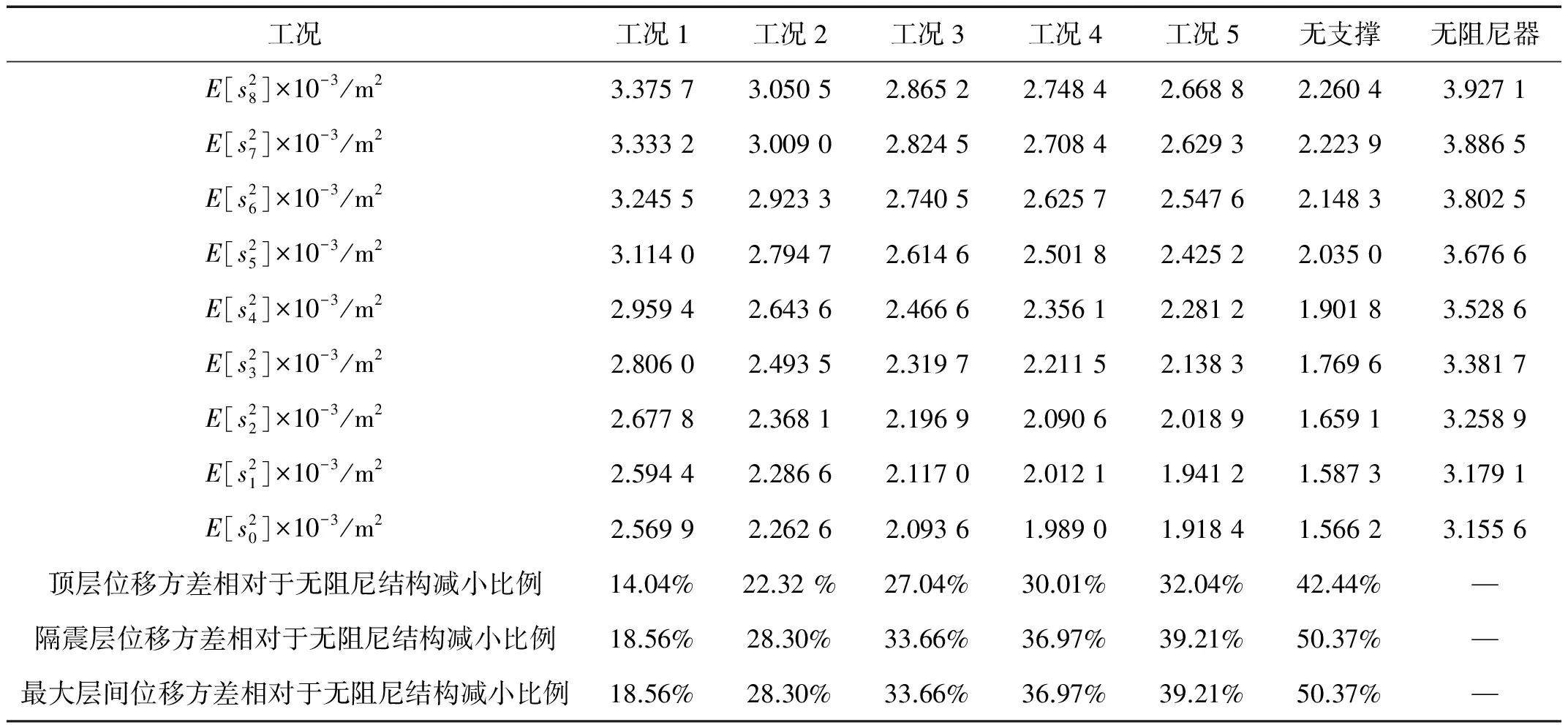
表1 结构各层位移方差

表2 结构各层速度方差

表3 阻尼器受力响应方差

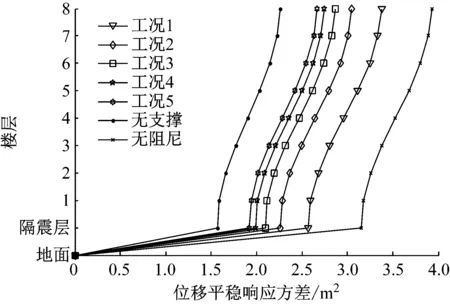
图3 Kanai-Tajimi谱下的位移方差

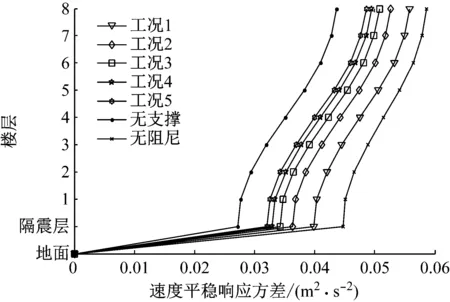
图4 Kanai-Tajimi谱下的速度方差

由表1、表2数据可看出在隔震层设置了阻尼器之后结构的位移和速度响应方差相对于无阻尼结构均减小了，且最大减小比例在隔震层处；由此可见，在隔震层设置阻尼器可有效抑制隔震层的地震响应。由表3数据可得随着支撑刚度的增加，阻尼器的受力也随之逐渐变大，也就是说，通过增加支撑刚度来增大阻尼器的受力可以减小结构地震响应，有效提高结构的耗能减震性能；算例表明，带支撑的阻尼器结构随着支撑刚度的无限增大，结构的位移、速度及阻尼器响应方差将无限逼近于不带支撑的阻尼器结构；而且，由图3、图4可直观看出，支撑刚度越大，各楼层相对地面的位移和速度响应方差越小，且均小于无阻尼结构的位移和速度响应方差，说明增加支撑刚度对提高结构的耗能减震效果有良好的作用。

5 结 论

本文对带支撑五参数Maxwell阻尼多层隔震结构在Kanai-Tajimi滤过白噪声激励下的平稳响应进行了研究。首先用第一振型展开，利用带支撑黏弹性阻尼的积分型分析模型建立了时域非扩阶精确建模，然后运用传递矩阵法获得了结构的位移、速度以及阻尼器的响应方差的解析解。计算结果比应用模态应变能和随机平均法等近似方法计算结果更为精确。算例分析还表明，支撑刚度对结构减震效果有着明显的影响，因此考虑支撑刚度更加符合工程实际情况。由于本文所得结构及阻尼器响应为解析解，因此可以更加方便地为隔震结构的隔震层参数、阻尼器及支撑刚度等参数的优化提供依据，更加有利于工程应用。

[1] 徐至钧, 徐卓, 赵尧钟, 等. 建筑结构隔震技术与应用[M]. 武汉: 同济大学出版社, 2014.

[2] CHRISTOPOULOS C, FILIATRULT A. Principle of passive supplemental damping and seismic isolation [M]. IUSS Press, Pavia, Italy, 2006.

[3] 周云. 黏弹性阻尼减震结构设计[M]. 武汉: 武汉理工大学出版社, 2006.

[4] PARK S W. Analytical modeling of viscoelastic dampers for structural and vibration control [J]. International Journal of Solids and Structures, 2001, 38(44/45): 8065-8092.

[5] CHANG T S, SINGH M P. Mechanical model parameter for viscoelastoc dampers [J]. Journal of Engineering Mechanics, 2009, 135(6): 581-584.

[6] SINGH M P, VERMA N P. Seismic analysis and design with Maxwell dampers [J]. Journal of Engineering Mechanics, 2003, 129(3): 273-282.

[7] YAMADA K. Dynamic characteristics of SDOF structure with Maxwell element [J]. Journal of Engineering Mechanics, 2008, 134(5): 396-404.

[8] PALMERI A, RICCIARDELLI F. State space formulation for linear viscoelastic system with memory [J]. Journal of Engineering Mechanics, 2003, 129(7): 715-724.

[9] PALMERI A. Correlation coefficients for structures with viscoelastic dampers [J]. Engineering Structures, 2006, 28(8): 1197-1208.

[10] 葛新广, 李创第, 邹万杰. Maxwell阻尼减震结构的最大非平稳响应[J]. 广西工学院学报, 2012, 23(4): 1-7.

GE Xinguang, LI Chuangdi, ZOU Wanjie.Maximum non-stationary earthquake response of structures with Maxwell viscous dampers[J]. Journal of Guangxi University of Technology,2012, 23(4): 1-7.

[11] 李创第, 李暾，尉宵腾，等. Maxwell阻尼耗能结构非平稳地震响应解析分析[J]. 振动与冲击, 2016, 35(19): 172-180.

LI Chuangdi, LI Tun, YU Xiaoteng, et al. Response analysis of energy dissipation structures with Maxwell dampers under no-stationary seismic excitation[J]. Journal of Vibration and Shock, 2016, 35(19): 172-180.

[12] SOONG T T, DARGRUSH G F. Passive energy dissipation systems in structural engineering [M]. England: John Wiley and Ltd,1997.

[13] ZHANG R H, SOONG T T. Seismic design of viscoelastic dampers for structural application [J]. Journal of Structural Engineering, 1992, 118(5): 1375-1392.

[14] 周云，松本達治，田中和宏，等. 高阻尼黏弹性阻尼器性能与力学模型研究[J]. 振动与冲击, 2015, 34(7): 1-7.

ZHOU Yun, MATSUMOTO Tatsuji, TANAKA Kazuhiro, et al. Performance and mechanical model of high damping viscoelastic dampers[J]. Journal of Vibration and Shock, 2015, 34(7): 1-7.

[15] 欧进萍, 吴斌, 龙旭. 消能减震结构的设计[C]. //戴国莹, 王亚勇.《建筑抗震设计规范》GB 57011-2001 背景材料. 中国建筑出版社, 2005: 323-330.

[16] 李创第, 邹万杰, 葛新广, 等. 多自由度一般积分型黏弹性阻尼器减震结构的随机响应与等效阻尼[J]. 工程力学, 2013, 30(4): 136-145.

LI Chuangdi, ZOU Wanjie, GE Xinguang, et al. Random response and equivalent damping of MDOF dissipation structures with general integral model viscoelastic dampers[J]. Engineering Mechanics, 2013, 30(4): 136-145.

[17] 吴克川，陶忠，韦光兰，等. 地震作用下防屈曲支撑减震结构附加有效阻尼比计算机变化规律研究[J]. 振动与冲击, 2016, 35(2): 146-152.

WU Kechuan, TAO Zhong, WEI Guanglan, et al. Calculation of the additional damping ratio of bucking-restrained brace structure and its variation under earthquake[J]. Journal of Vibration and Shock, 2016, 35(2): 146-152.

[18] ZAMBRANO A, INAUDI J A, KELLY J M. Modal coupling and accuracy of modal strain energy method[J]. Journal of Engineering Mechanics, 1996, 122(7):603-612.

[19] 李创第, 李暾, 葛新广, 等. 一般线性黏弹性阻尼器耗能结构瞬态响应的非正交振型叠加精确解[J]. 工程力学, 2015, 32(11): 140-149.

LI Chuangdi, LI Tun, GE Xinguang,et al. Exact non-orthogonal modal superposition solutions of transient response of MDOF dissipation structrures with general linear viscoelastic dampers[J].Engineering Mechanics, 2015, 32(11): 140-149.

[20] 廖伯瑜, 周新民, 尹志宏. 现代机械动力学及其工程应用: 建模、分析、仿真、修改、控制、优化[M]. 北 京: 机械工业出版社, 2003:175-179.

[21] 李创第, 陈欧阳, 葛新广, 等. 高层隔震结构实空间解耦及地震作用取值分析[J]. 振动与冲击, 2014, 33(15): 119-125.

LI Chuangdi, CHEN Ouyang, GE Xinguang, et al. Decoupling in a real space and earthquake action analysis for high-rise isolatedstructures[J]. Journal of Vibration and Shock, 2014, 33(15): 119-125.

[22] 李创第, 高硕, 葛新广, 等. 五参数Maxwell阻尼器耗能结构在有界噪声激励下随机响应解析解[J]. 广西科技大学学报, 2016, 27(3): 1-7.

LI Chuangdi, GAO Shuo, GE Xinguang,et al. Analytic solution of random response of energy dissipation structures with five-parameter Maxwell dampers under bounded noise excitation[J]. Journal of Guangxi University of Science and Technology, 2016, 27(3): 1-7.

[23] 方同. 工程随机振动[M]. 北京: 国防工业出版社, 1995.

[24] 胡聿贤. 地震工程学[M]. 2版. 北京: 地震出版社, 2006.

Randomseismicresponsesofmulti-layervibrationisolationstructuresmountedwithsupporterattachedMaxwelldampers

ZOUWanjie，MAYuan，LIChuangdi，GEXinguang

(Department of Civil Engineering, Guangxi University of Science and Technology, Liuzhou 545006, China)

The analytical solutions of stochastic seismic responses and steady state responses of a multi-storey base isolation structure whose isolation layers were mounted with five parameters Maxwell dampers attached with supporters were studied. The upper structure was expanded by thefirst vibration mode shape and then by using the integral type analysis model for the supporter attached five parameters Maxwell damper, a non-extended accurate model for the structure was realized in time domain by using the integral-differential equations. By using the transfer matrix method, the analytic expressions in original structural space for the displacement, velocity and damper transient responses of the multi-layer isolation structure in time domain under arbitrary excitations were obtained. Finally,based on the analytical solutions,the random response variances of the displacement, velocity and damper’s force of the multi-layer isolation structure under Kanai-Tajimi stationary filtered white noise excitations were obtained. A complete analytical method for solving the stochastic responses of multi-layer isolation structures under Kanai-Tajimi filtered white noise excitations was thus established. A numerical example was given to verify its effectiveness.

five-parameters Maxwell damper; supporting; multi-layer isolation structure; transfer matrix method; damper’s force

TU352.1

A

10.13465/j.cnki.jvs.2017.21.031

国家自然科学基金(51468005)；广西自然科学基金(2011GXNSFA018032;2014GXNSFAA118315)；广西科技大学创新团队支持计划

2016-10-12 修改稿收到日期：2017-01-18

邹万杰 男，副教授，博士，1974年生