夹层边界上布置主动声学边界的有源隔声双层板结构

宁少武， 史治宇， 胥馨尹

(1. 南京航空航天大学 机械结构力学及控制国家重点实验室， 南京 210016; 2. 中国工程物理研究院总体工程研究所， 四川 绵阳 621900)

夹层边界上布置主动声学边界的有源隔声双层板结构

宁少武1， 史治宇1， 胥馨尹2

(1. 南京航空航天大学 机械结构力学及控制国家重点实验室， 南京 210016; 2. 中国工程物理研究院总体工程研究所， 四川 绵阳 621900)

在双层板结构中夹层声场边界上布置平面声源作为主动声学边界，构成有源隔声双层板结构，提出基于主动声学边界方法的有源隔声双层板结构。在双层板结构中夹层边界上布置四边简支板，用来代替主动声学边界，控制力作用到该简支板上，采用声弹性理论建立了有源隔声双层板结构的计算模型，分别以辐射声功率最小和夹层声功率最小作为控制目标来优化控制力，计算分析控制前后夹层结构的传声损失以及各子系统的响应，并研究了主动声边界尺寸大小对系统隔声性能的影响。计算结果表明：主动声边界控制策略可以有效提高双层板结构的隔声性能，且以辐射声功率最小为控制目标要优于以夹层声场的声功率最小为控制目标；控制后，主动声边界对入射板振动响应几乎没有影响，辐射面板的振动动能和夹层声场的声功率均被有效地抑制；不同尺寸主动声边界都提高了夹层结构的隔声性能；对于低频率段，不同尺寸主动声边界对夹层结构的隔声性能提高的程度相同；对于其他频率段，主动声边界对传声损失和各子系统响应的影响并没有一定的规律，可以对主动声边界的尺寸进行优化设计，达到提高特定频段隔声性能的目的。

主动声学边界方法; 声弹性理论; 声传递损失; 有源隔声双层板结构; 辐射声功率

轻质板壳结构广泛应用于工程领域，如车辆、船舶、飞机机舱结构等，然而，随着运行速度和乘坐舒适性要求的不断提高，对板壳结构的振动和声辐射问题越来越引起人们的重视。由质量作用定律[1]知道，对于一定频率的声波，一个密实单层板的隔声量，唯一决定因素是单位面积的质量，且对低频的隔声比高频的隔声更加地困难。利用双层板结构，对于高频噪声，随着板间距的增加，隔声量越大，然而，对于很低频率的噪声，双层板结构并不比合在一起的单层板结构优越，这是由于‘板-空气-板’共振现象引起双层板结构隔声性能的降低[2]。

对于噪声控制问题，从技术来讲，可以分为被动控制和主动控制两种。被动控制如吸声、隔声、消声等，即通过噪声声波与声学材料或声学结构的相互作用消耗声能。然而，被动控制方法对控制中高频噪声是有效的，对低频噪声的控制效果不大。对于低频噪声控制问题，人们提出了主动噪声控制方法。特别地，对于结构声辐射或声透射的研究，提出了结构声有源控制(Active Structural Acoustic Control, ASAC)[3]。

Pan等[4]研究了板-腔声振耦合问题，指出在板-腔耦合系统中存在板控制模态和腔控制模态；对于利用点力控制声波穿过简支板进入声腔的噪声控制问题，Lee等[5]指出对于板控制模态，通过抑制相应的板控制模态实现噪声控制，对于声腔控制模态，则通过调整平板的速度分布实现辐射到声腔的声功率的降低。Pan等[6]研究了利用力源和声源控制声传入声腔的问题，研究指出力源可以有效控制结构控制模态，声源可以有效控制声腔控制模态，而对于结构和声腔控制模态共同支配的声场，同时利用力源和声源可以得到理想的噪声控制效果。Pan等[7]研究了利用声源或力源控制矩形平板的远场声辐射主动噪声控制问题。Kim等[8]研究了采用长条压电片控制线分布弯矩激励下矩形平板的声辐射主动控制问题，指出了模态抑制和模态重构的控制机理以及激励力位置和压电片(控制器)位置对噪声控制效果的影响。

对于双层板结构的主动噪声控制问题，Pan等[9]从理论上研究了采用不同的控制途径对双层板结构声传输实施控制问题，分析了各个控制途径存在的控制机理，指出存在模态抑制和模态重构两种控制机理。Carneal等[10]研究了双层板结构声传输的有源噪声控制问题，研究表明高刚度的辐射面板以及控制力作用于辐射面板能获得更大地提高结双层板结构的隔声性能。靳国永等[11]基于声辐射模态研究了双层板结构声传输的有源控制问题。Li等[12]研究了有机械连接的双层板结构声传输的有源控制问题，表明声波的传递路径决定了控制策略的选择，以及存在模态抑制和模态重构的有源噪声控制机理。Pieztrzko等[13]对比研究了目前在双层板结构声传输的主被动控制问题的方面的研究成果。

上述研究表明，结构声有源控制可以显著提高结构在低频段的隔声性能。然而，由于控制力直接作用于结构表面，往往会引起结构的疲劳；对于类似于飞机舷窗的双层板结构，在结构上布置控制元件或在夹层中布置控制声源会影响乘客的视线，甚至会影响结构的功能[3]。基于此，提出夹层边界上布置主动声学边界的控制策略，建立双层板结构的结构声有源控制模型。与前面不同之处在于，在夹层结构的夹层边界上布置主动控制面，即主动声边界，实现夹层结构隔声性能的提高，特别是对于低频段。本文中，对于主动声边界，采用镶嵌于夹层边界的简支平板来模拟，即主动声边界板，控制力作用在主动声边界板上，应用声弹性理论[14]，建立系统中子系统之间的耦合关系，分别以辐射声功率最小和夹层声场的声功率最小为控制目标计算最优控制力，仿真验证文中控制策略的可行性，分析其控制机理，对比不同控制目标和主动声边界板尺寸大小对噪声控制效果的影响。

1 有源隔声夹层板结构系统模型计算

如图1所示，建立双层板夹层结构，夹层厚度为h，在夹层边界上布置主动声学边界。本文中将主动声学边界等效为四边简支的弹性板，控制力作用在该简支弹性板上。上下面板的长度和宽度分别为a和b，厚度分别为t1和t2，上下弹性面板的振动控制方程为

(1)

(2)

式中：Di为弹性板的弯曲刚度；mi为弹性板的面密度；wi为弹性面板的振动位移；i=1,2。Pin为入射声场声压，忽略入射侧弹性面板向入射声场辐射声波，则入射声场的声压Pin可以表示为

Pin=2Pin0e-jkxx+kyy+kzz-ωt

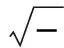
kx=k0sinθcos ϑ

ky=k0sinθsin ϑ

kz=k0cosθ

式中：k0=ω/c0，c0为空气中声速；θ为入射角；ϑ为方位角。pg和pr分别为夹层声场和辐射声场的声压，其满足的控制方程为

(3)

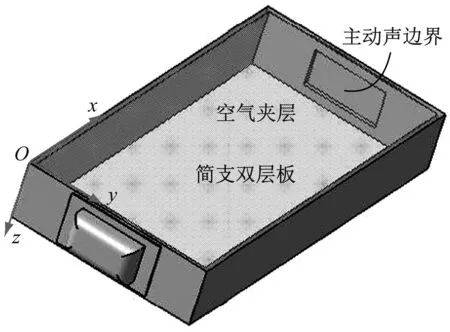
(a) 三维模型

(b) 计算模型

Fig.1 Schematic of active double-panel sound insulation structure based on active acoustical boundary

同理，主动声边界板的振动控制方程分别为

(4)

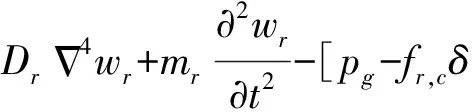
(5)

式中：Dl和Dr、ml和mr以及wl和wr分别为左右两侧主动声边界弹性板的弯曲刚度、面密度、横截面积和振动位移。fl,c和fr,c、yl,c,zl,c和yr,c,zr,c分别为施加在左右两侧主动声边界弹性板上的控制力大小和作用在主动声边界板上的位置，δ·为δ函数。

上下弹性面板简支安装在声障上，其满足的边界条件为

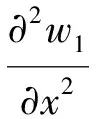
(6a)

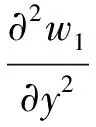
(6b)

同理，左右两侧主动声边界板也简支安装在夹层声场的刚性边界上，其满足的边界条件分别为

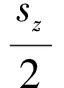
(7a)

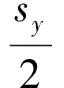
(7b)

式中:yc,zc为左右两侧主动声边界板的中心坐标，sy和sz分别为左右两侧主动声边界板的几何尺寸。

在结构与声场的边界上，满足的边界条件为

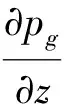
(8a)

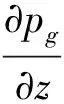
(8b)

(8c)

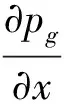
(8d)

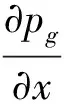
(8e)

同时，夹层声腔中其他边界均假设为声学刚性边界。

双层板结构的上下面板为简支支撑，则其振动位移可以表示成简支模态函数的形式

w1(x,y;t)=φT(x,y)α1TejTωt

(9a)

w2(x,y;t)=φT(x,y)α2TejTωt

(9b)

式中:α1和α2分别上下两弹性板的振动模态系数向量;φ(x,y)为其相应的简支模态函数。同理，对于简支支撑的主动声学边界板的振动位移表示成简支模态函数的形式

wl(y,z;t)=ψT(y,z)αlejωt

(10a)

wr(y,z;t)=ψT(y,z)αrejωt

(10b)

式中:αl和αr分别左右两侧主动声学弹性板的振动模态系数向量;ψ(y,z)为相应的简支模态函数。辐射声场的声场分布表示为结构模态函数的组合形式，即

pr(x,y,z;t)=φT(x,y)ζe-j[kz(z-h)-ωt]

(11)

式中：ζ为声场声压系数向量。夹层声场表示为夹层声场模态函数的叠加形式为

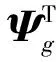
(12)

式中：Ψgx,y,z为夹层声场的模态函数向量，μ为相应的模态系数向量。夹层声场的模态函数Ψgx,y,z

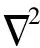
(13)

式中：Ωg为刚性声腔的固有模态频率矩阵。

由边界条件式(8c)，可得

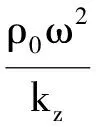
(14)

应用声弹性理论[14]，由格林公式

(15)

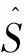
Lgμ=-T1,gα1+T2,gα2-Tl,gαl+Tr,gαr

(16)

式中，

对于双层板结构的上面板，将式(9a)代入式(1)，利用振动模态函数的正交性，引入结构阻尼系数χ1，则有

(17)

式中，

令

则有

Z1,sα1+Γ1,gμ=F

(18)

同理，将式(9b)代入式(2)，同样利用振动模态函数的正交性，引入结构阻尼系数χ2，可以得到

(19)

式中，

令

则有

Z2,sα2-Γ2,gμ=0

(20)

对于主动声学边界板，将式(10a)代入式(4)，利用模态函数的正交性，并引入结构阻尼系数χl，则有

(21)

式中，

令

则有

Zl,cαl+Γl,cμ=ψ(yl,c,zl,c)fl,c

(22)

同理，将式(10b)代入式(5)，利用模态函数的正交性，引入结构阻尼系数χr，则有

(23)

式中，

令

则有

Zr,cαr-Γr,cμ=-ψ(yr,c,zr,c)fr,c

(24)

2 最优控制力

对于双层板结构的噪声主动控制问题，目的在于提高系统的隔声性能，降低结构向辐射空间辐射噪声。从声波在夹层结构中传播的路径来讲，可以从以下两方面来考虑：

(1) 以辐射声功率最小为控制目标，直接降低辐射声场的声功率，定义辐射声场的平均辐射声功率为

(25)

(2) 切断声波传递的路径，降低声波传递路径中声功率，即以夹层声场中声功率最小为控制目标，定义夹层声场的平均声功率为

(26)

首先，由式(18),(22),(24)可以得到

(27a)

(27b)

(27c)

将式(27)代入式(16)，可以得到

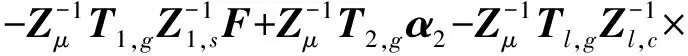
(28)

其中，

将式(28)代入式(20)，则有

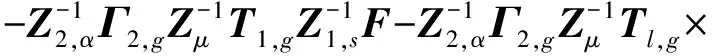
ψyr,c,zr,cfr,c

(29)

其中，

令

则式(29)可以表示为

α2=Ξr,p+Ξr,cfc

(30)

因此，由式(11)和式(30)可以得到辐射声场的辐射声压为

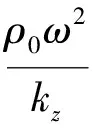
(31)

其次，由式(20)可以得到

(34)

将式(27)和(34)代入式(16)，则有

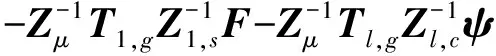
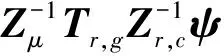
(35)

其中

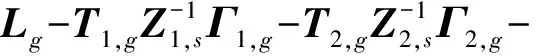
令

则式(35)可以表示为

μ=Ξg,p+Ξg,cfc

(36)

因此，由式(12)和式(36)，夹层声场的声压分布为

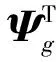
(37)

那么，将式(31)代入式(25)，或将式(37)代入式(26)，整理可以得到

(38)

式中，

其中，i=r,g，其中Mi分别取为

(39a)

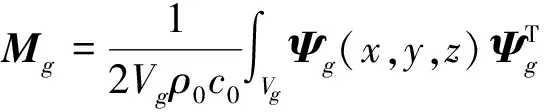
(39b)

因此，由式(38)得到相应的最优控制力为

(40)

则夹层声场的平均声功率的最小值等于

(41)

实际上，cA为没有控制力作用时辐射声场或夹层声场的平均声功率。

假设入射声场的平均声功率为WI，辐射声场的平均声功率为Wr，夹层声场的平均声功率为Wg。定义结构的传声损失为

(42)

定义结构的平均振动动能为

(43)

式中:i可以根据计算的需要取为辐射面板(下面板)，下面板的平均振动动能Elow，以及左侧主动声边界板，即左侧主动声边界板的平均振动动能Ec,l。

3 仿真分析

为了验证控制策略的可行性以及探索控制机理，建立了如图1所示的仿真计算模型。双层板结构系统采用与文献[15]相同的结构参数。上下面板(入射面板和辐射面板)的长度a=0.8 m, 宽度b=0.7 m, 厚度分别为t1=3 mm和t2=4 mm, 杨氏模量E=71 GPa, 密度ρ=2 720 kg/m3， 泊松比ν=0.33。空气夹层厚度为h=160 mm, 空气密度ρ0=1.21 kg/m3, 声速c0=343m/s, 入射角θ=30°, 方位角ϑ=30°，声压幅值Pin0=1.0 m2/s。左右两侧主动声边界板的各尺寸相同，板的长度sy=0.3 (或0.2, 0.4) m, 宽度sz=0.08 (或0.06, 0.1) m, 厚度tc=1 mm, 杨氏模量Ec=0.90 GPa, 密度ρc=950 kg/m3， 泊松比νc=0.38。假设系统中各子系统的损耗因子均为0.01。为了保证激发出足够的模态，控制力作用位置坐标yl,c,zl,c和yr,c,zr,c均为(0.25sy, 0.25sz)。整个系统的计算频段0～500 Hz。为了使得选取的模态阶数覆盖整个计算频段，对于双层板结构选取的模态阶数为(10,10)，对于夹层声腔选取的模态阶数为(5,5,1)，对于控制面板选取的模态阶数为(10,3)。

图2为控制前后双层板系统的传声损失曲线。从图中可以看出：0～70 Hz和220～500 Hz区间内，以辐射声功率为控制目标优于以夹层声功率为控制目标提高了夹层结构的隔声性能。在70～220 Hz之间，两种控制目标下同样提高了夹层结构的隔声性能，但两者对结构的隔声性能的改善基本没有区别。

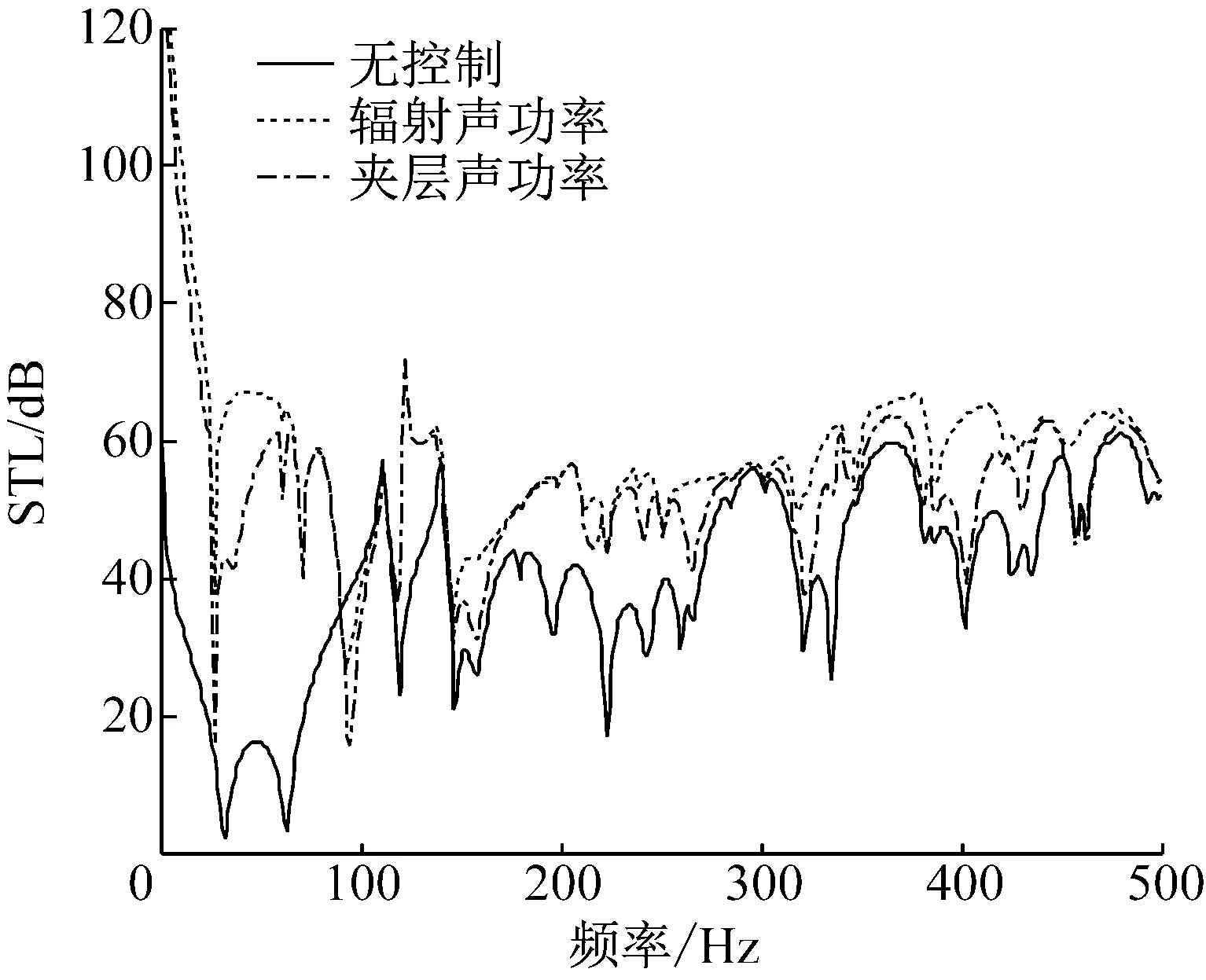
图2 在不同控制目标下简支双层板系统的传声损失曲线

Fig.2 Comparison of STL of simply supported double-panel systems by using the active acoustical boundary with different control objectives

下面来说明控制前后系统中各部分能量的变化。首先，对于入射面板的平均动能，经计算，在控制前后基本变化不大。后面的分析中主要来说明辐射面板(下面板)，夹层声场和辐射声场在控制前后的能量变化情况。图3～图5分别为对比了在控制前后在不同控制目标下，下面板平均动能曲线、夹层声场平均声功率曲线以及辐射声场平均声功率曲线。首先，为了验证计算结果的正确性，与文献[15]中控制前系统中各个子系统的动态性能随频率的变化曲线对比。文献[15]中计算了夹层声场的势能，辐射面板的动能以及辐射声场的声功率，虽与图3～图5中定义有所不同，但均反映了系统的动态性能，对比可以看出具有相同的变化趋势和相同的峰值和低谷，从而保证本文计算结果的正确性。

从图3中可以看出，在控制前后，辐射面板的振动被有效地抑制。从图4中可以看出，在控制前后夹层声场的平均声功率发生明显变化，即声功率明显降低，但两种控制目标下夹层声场声功率大小区别基本不大。

从声传递的路线来讲，入射面板激发空气夹层传递能量，产生声波；主动声边界板同样激发空气夹层传递能量，产生声波；两种声波在夹层中相互作用，改变夹层声场声压分布，同时诱发辐射面板振动，从而向辐射声场辐射噪声。从图3和图4可以看出，在控制前后，夹层声功率和辐射面板动能降低，但曲线中不同的尖峰和低谷的出现反映了辐射面板振动模态与夹层声场模态以及主动声边界板振动模态与夹层声场模态之间的耦合程度。

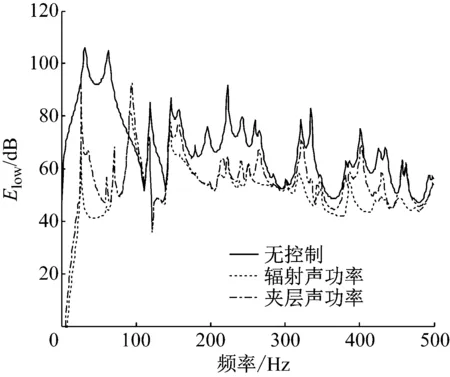
图3 在不同控制目标下简支双层板系统中下面板的振动动能

Fig.3 Comparison of averaged kinetic energy of the lower panels for simply supported double-panel systems by using the active acoustical boundary with different control objectives

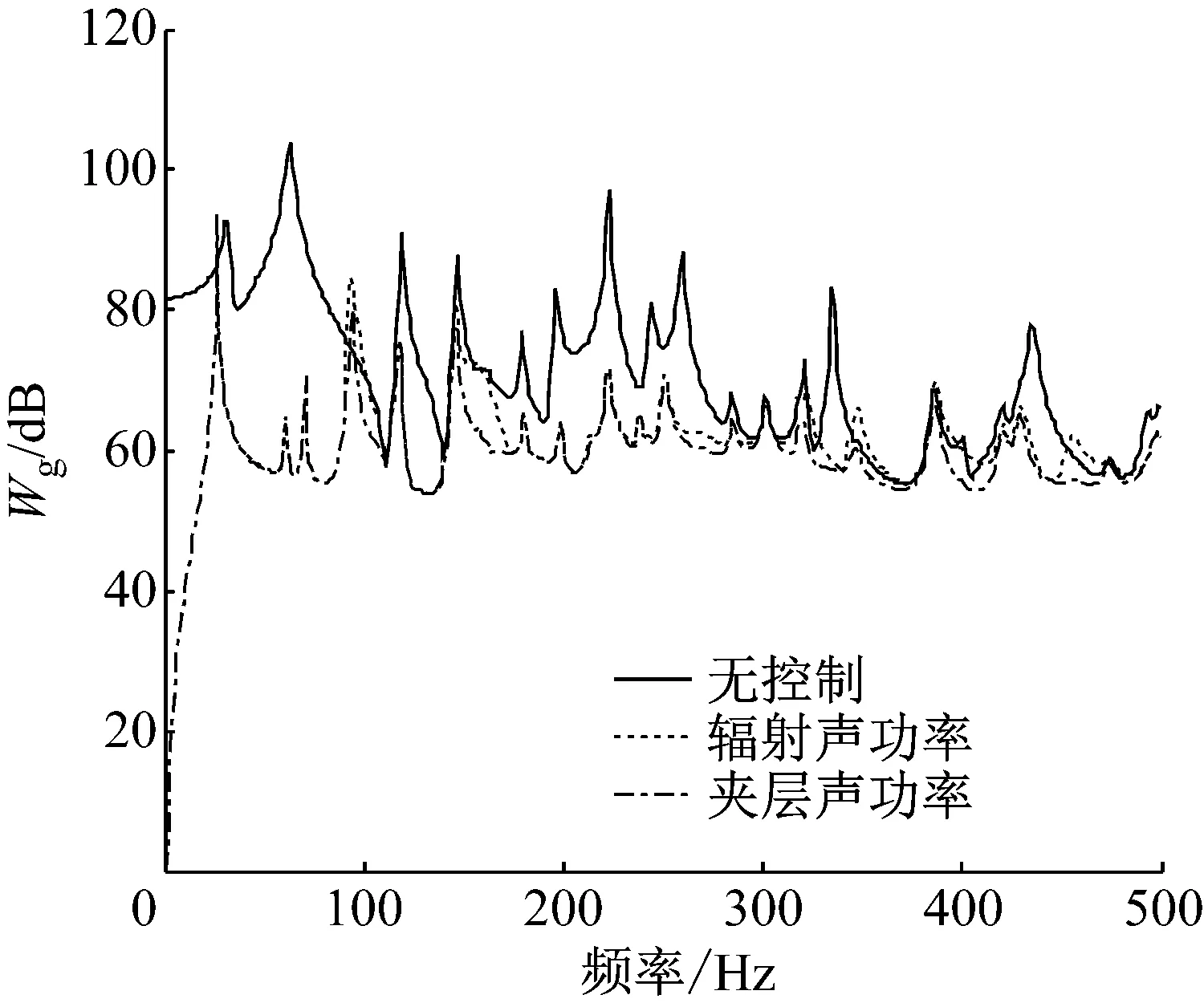
图4 在不同控制目标下简支双层板系统中夹层声场的声功率

Fig.4 Comparison of sound power of the gap sound filed for simply supported double-panel systems by using the active acoustical boundary with different control objectives

图5 在不同控制目标下简支双层板系统中辐射声场的声功率

Fig.5 Comparison of sound power of the radiating sound filed for simply supported double-panel systems by using the active acoustical boundary with different control objectives

从式(11)可知，辐射声场的声压采用辐射面板的振动模态表示，从图(3)和图(5)也可以看出辐射声场的辐射声功率与辐射面板动能基本相同，相比以夹层声功率最小为控制目标，以辐射声功率最小为控制目标获得了更好的控制效果，即辐射结构动能和辐射声功率更小。

为了进一步说明噪声控制机理，计算分别在50 Hz, 110 Hz和400 Hz时，辐射面板前20阶阶振动模态平均动能和夹层声场前20阶声模态平均声功率在控制前后的变化情况。

图6(a)～6(b)分别为在50 Hz时，辐射面板的平均模态振动动能和夹层声场的平均模态声功率。实际上，50 Hz位于辐射面板结构第一阶(1,1)模态频率35.37 Hz和第二阶(2,1)模态频率81.39 Hz之间，更远小于夹层声腔第一阶非零声模态频率214.38 Hz。经计算，从图6(a)可以看出，无控制时，结构所有的(奇，奇)结构模态对结构振动的贡献大，其中，辐射面板的(1,1)阶模态频率为主导模态频率。在不同的控制目标下，辐射面板对应的各阶(奇,奇)模态均得到有效的抑制，且以辐射声功率为控制目标获得的振动抑制效果更优。总的来看，在50 Hz时，主动声边界对辐射面板的作用表现为模态抑制。由于辐射面板直接与辐射声场相互作用，从而降低了辐射面板向辐射声场辐射声功率。

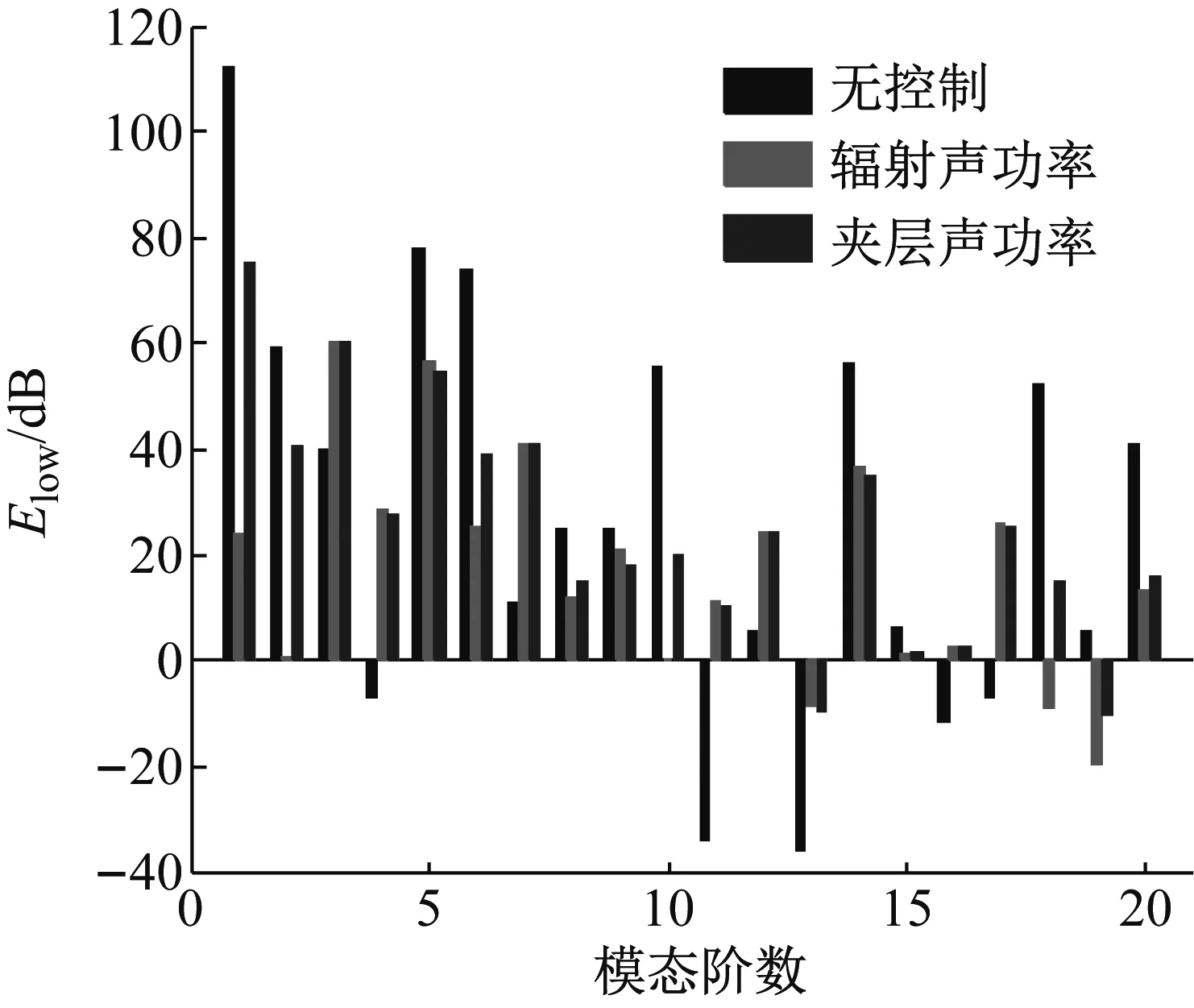
(a) 下面板的平均模态振动动能

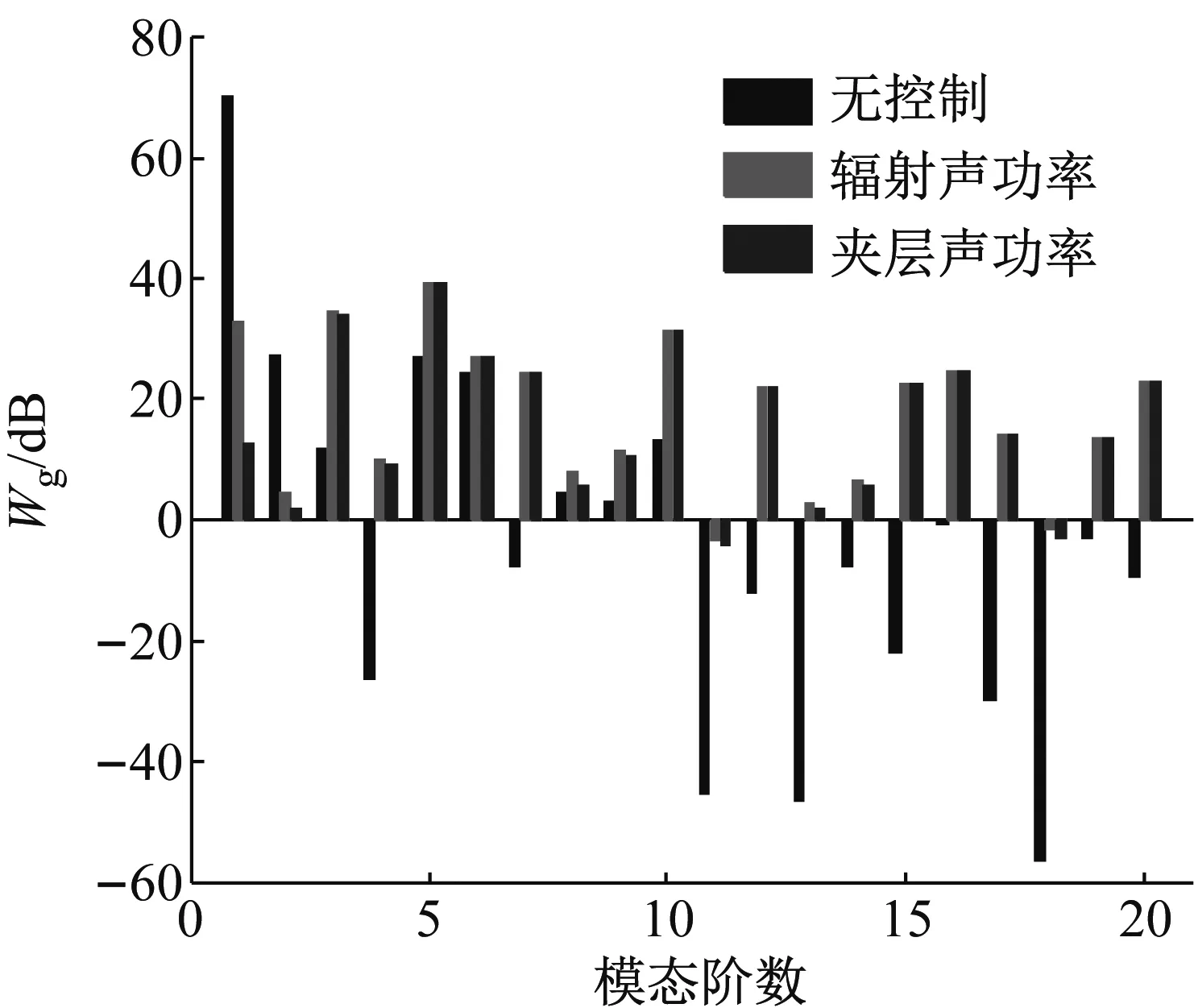
(b) 夹层声场的平均模态声功率

Fig.6 Modal power of subsystems of simply supported double-panel systems with different control objective for driving frequencyf=50 Hz

从图6(b)可以看出，在50 Hz时，夹层声场的(0,0,0)阶(第一阶)模态为主导模态。控制前后对比可以看出，夹层声场的(0,0,0)模态被有效抑制，且以夹层声功率最小为控制目标得到的抑制效果更好。然而，也可以看出在控制后其他模态的声功率均不同程度有所增加，但不足以改变声功率被抑制的总效果；也可以看到在不同控制目标下模态声功率变化略有所不同。因此，图4中50 Hz时，夹层声功率被有效抑制，且不同目标函数下控制后夹层声功率基本相同。从控制机理来讲，表现为模态抑制。

从图2可以看出，在110 Hz附近结构的传声损失并没有改善。为了说明其原因，选取110 Hz，计算相应的辐射面板的平均模态振动动能和夹层声场的平均模态声功率，如图7(a)～7(b)所示。从图7中可以看出，在控制前后，辐射面板平均模态动能在有些模态被抑制，在有些模态反而提高。同理，对于夹层声场的的平均模态声功率也是如此。从而引起在110 Hz附近时结构的传声损失并没有得到改善。

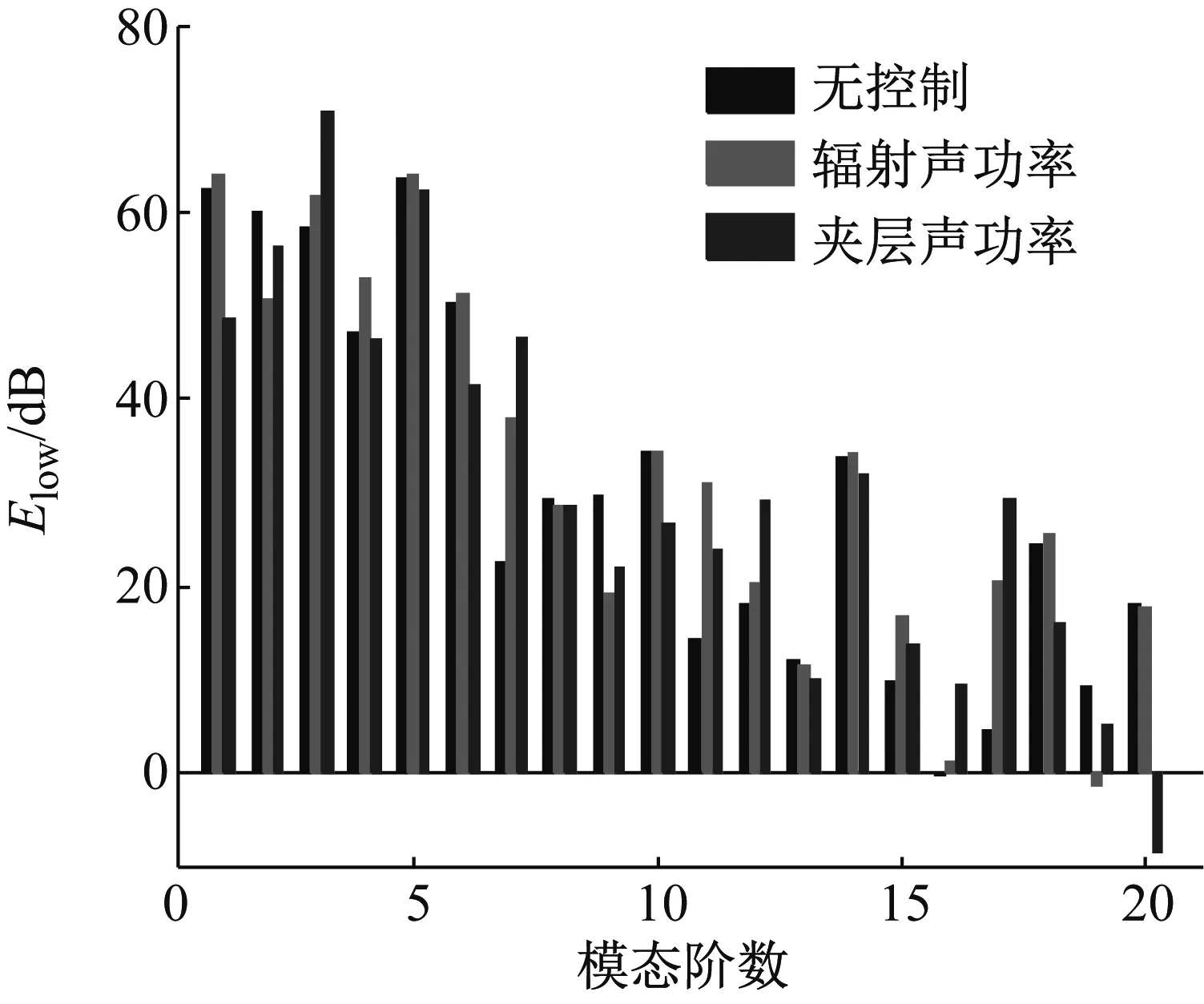
(a) 下面板的平均模态振动动能

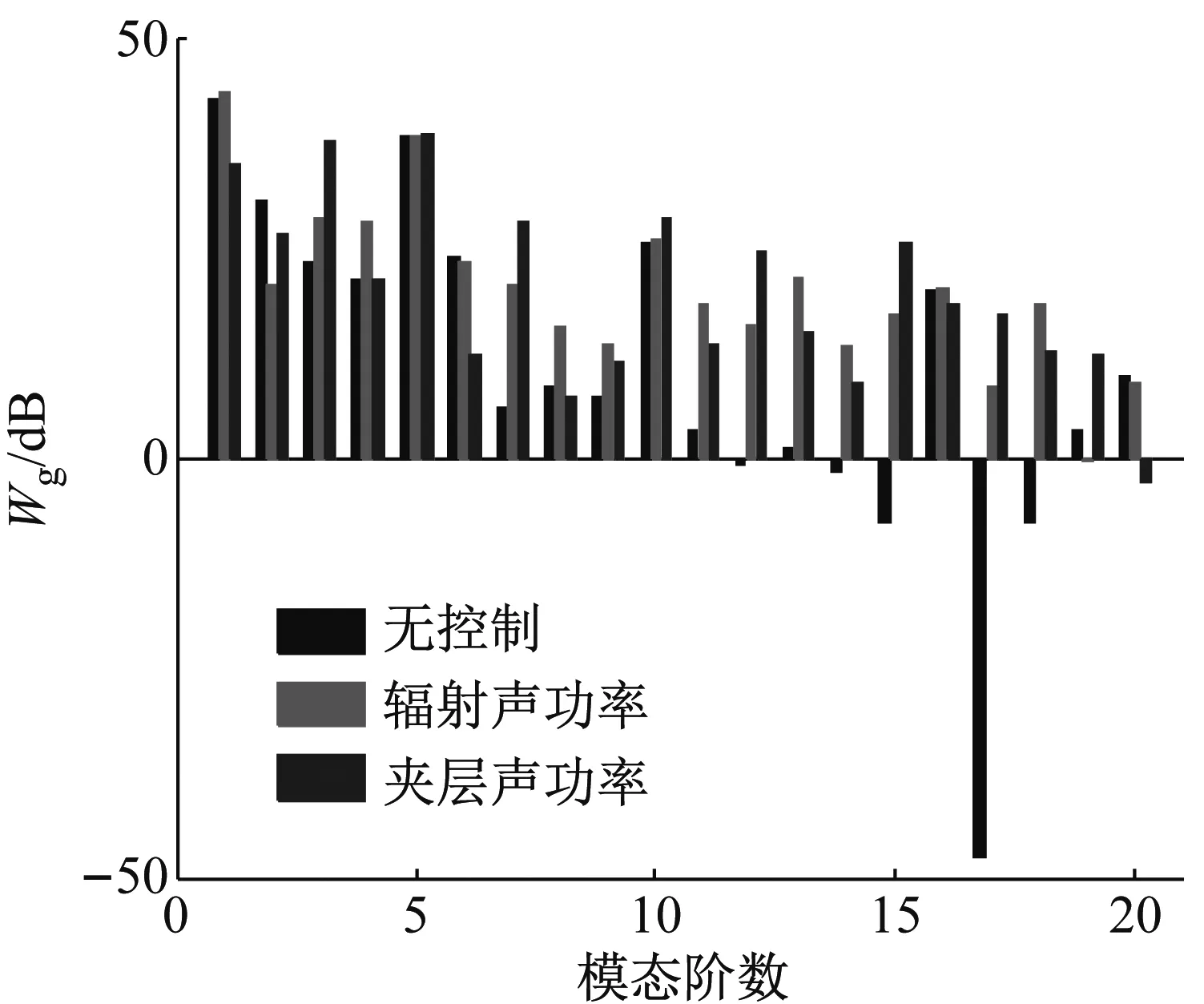
(b) 夹层声场的平均模态声功率

Fig.7 Modal power of subsystems of simply supported double-panel systems with different control objective for driving frequencyf=110 Hz

图8(a)～8(b)为400 Hz时，辐射面板的平均模态振动动能和夹层声场的平均模态声功率。实际上，400 Hz紧邻辐射板的第14阶(5,1)模态频率403.5 Hz。从图11(a)也可以看出，对应辐射面板的第14阶振动模态为主导模态，在控制前后，其被有效地抑制；同时，其中(3,1)阶模态158.08 Hz也被有效地抑制。虽然(1,1)模态在控制后有所增加，但没有根本削弱对辐射面板振动响应的抑制效果。对于其他模态，控制前后变化很小。总之，控制机理表现为模态抑制。同时也可以看出，以辐射声功率最小为控制目标，更好地抑制了辐射面板的振动模态响应，这是由于辐射面板直接与辐射声场相互作用，决定了辐射声功率的大小。

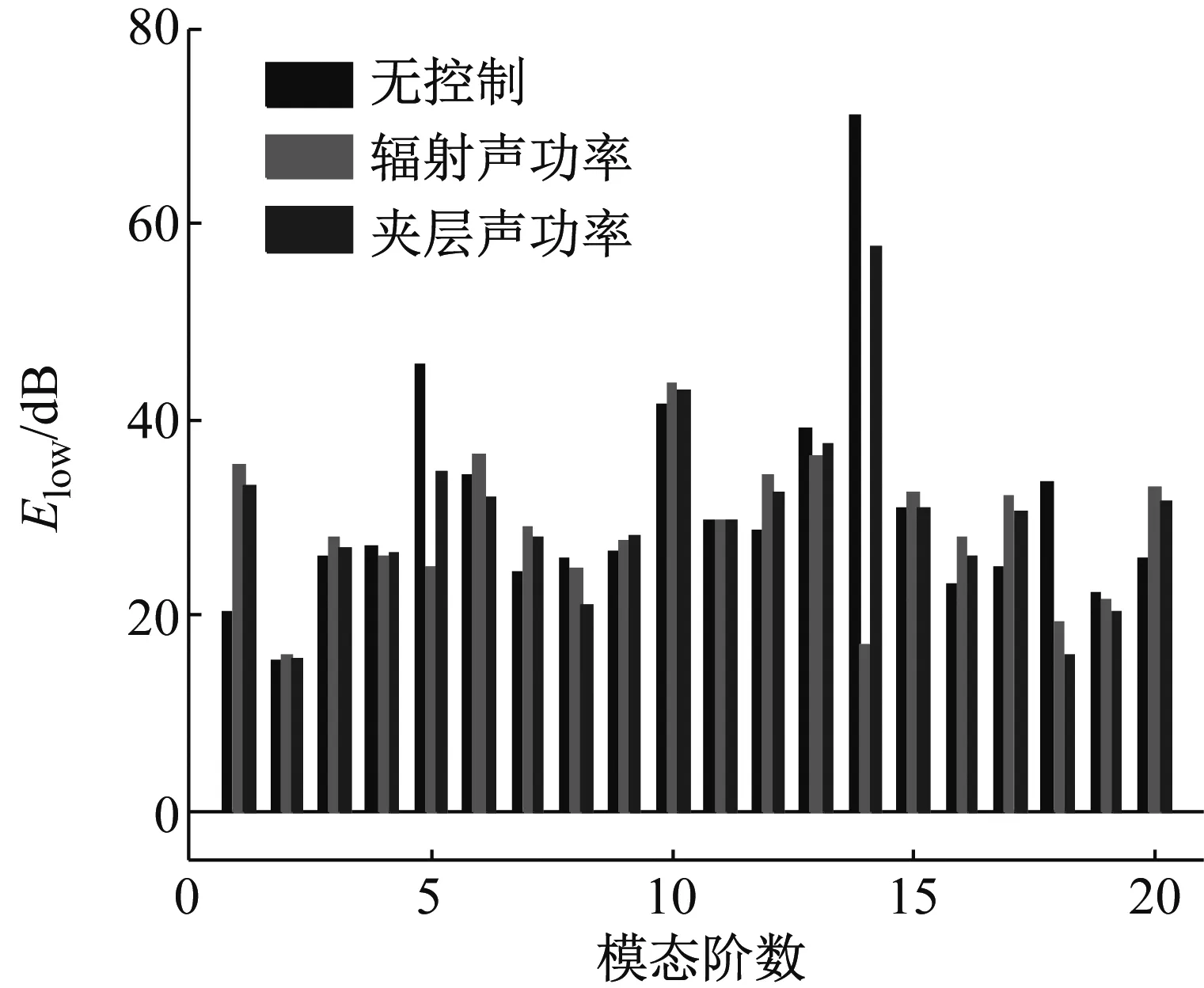
(a) 下面板的平均模态振动动能

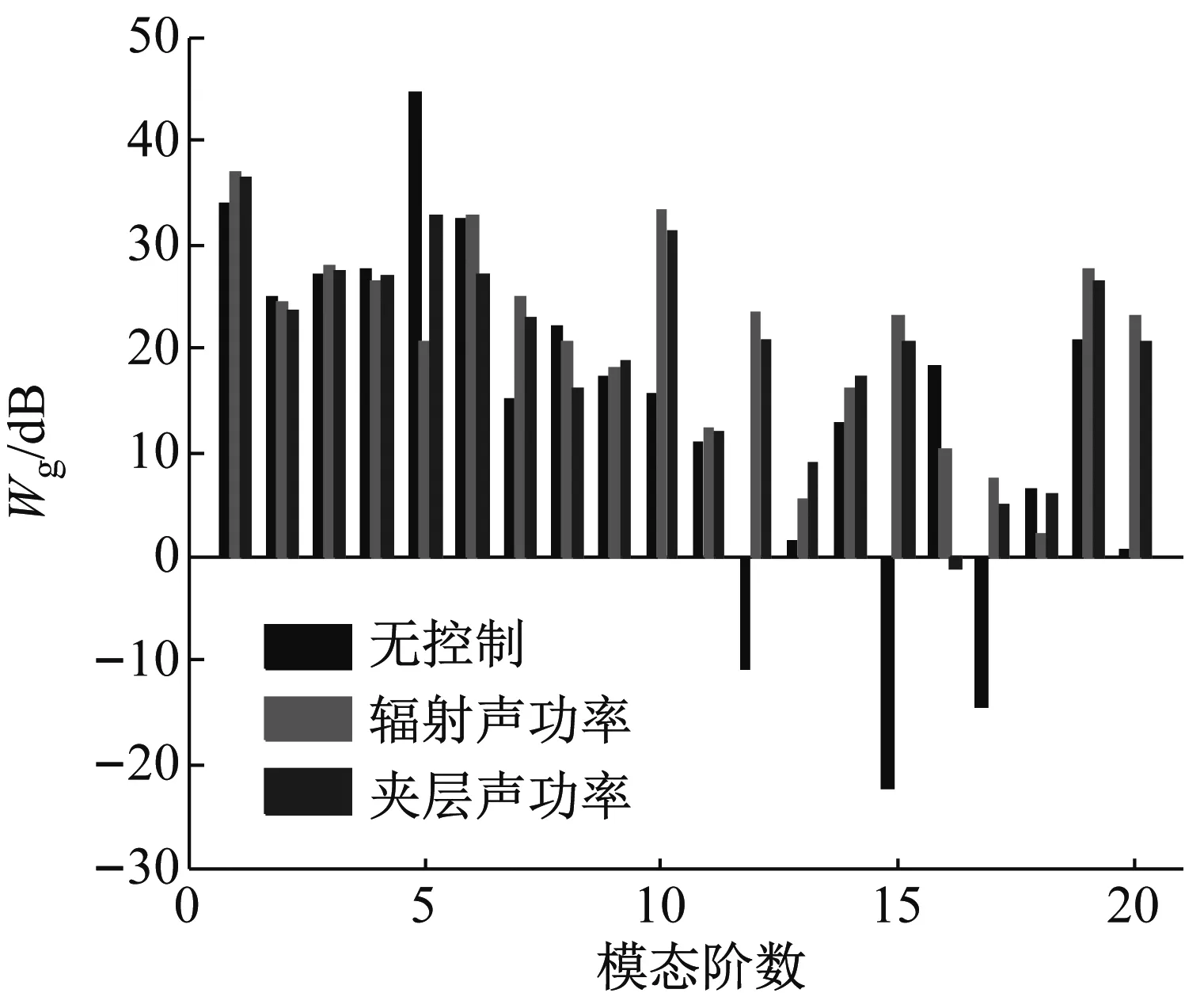
(b) 夹层声场的平均模态声功率

Fig.8 Modal power of subsystems of simply supported double-panel systems with different control objective for driving frequencyf=400 Hz

从图8(b)可以看出，夹层声场中(2,0,0)阶(第5阶, 428.75 Hz)模态为主导声模态，在控制前后，该阶模态被有效地抑制。特别对于有些模态，如(2,2,0)阶(第10阶, 651.01 Hz)模态，在控制后对应的模态声功率明显增加。从图4和图5中可以看到，在400 Hz处，夹层声功率在控制前后虽有所改变，但变化很小，而辐射面板的动能在控制前后发生了很大的变化，均明显降低，且以辐射声功率最小为控制目标降低的幅度更大。

图9(a)和图9(b)分别为以辐射声功率最小和以夹层声功率最小化为控制目标，采用不同尺寸主动声边界，夹层结构在控制前后板获得的传声损失曲线。如前所述，从图9(a)和图9(b)中可以看出，相比以夹层声场声功率最小为控制目标，以辐射声功率最小作为控制目标获得了更大的结构传声损失。从图中可以看出，在0～50 Hz区间，三个尺寸的主动声边界获得传声损失相同；控制后，在70 Hz附近，0.4 m×0.1 m的主动声边界相比其他两者反而使得结构传声损失降低；对于100 Hz左侧频率位置，0.3 m×0.08 m的主动声边界板使得夹层结构的隔声性能极大地恶化，比控制前的隔声性能还要差；200 Hz的左侧附近区间，0.3 m×0.08 m的主动声边界相比其他两者在明显提高了夹层结构的传声损失；在大于200 Hz的频率区间，虽都一定程度提高了夹层结构的隔声性能，但结构尺寸的影响并没有表现出一定规律。

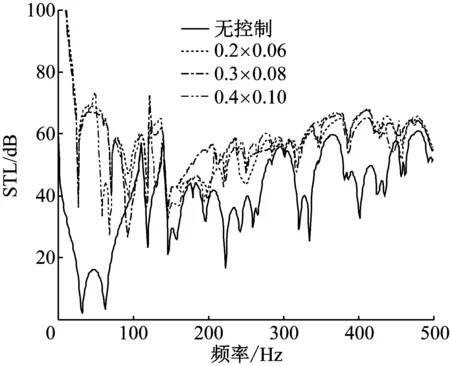
(a) 以辐射声功率最小为控制目标

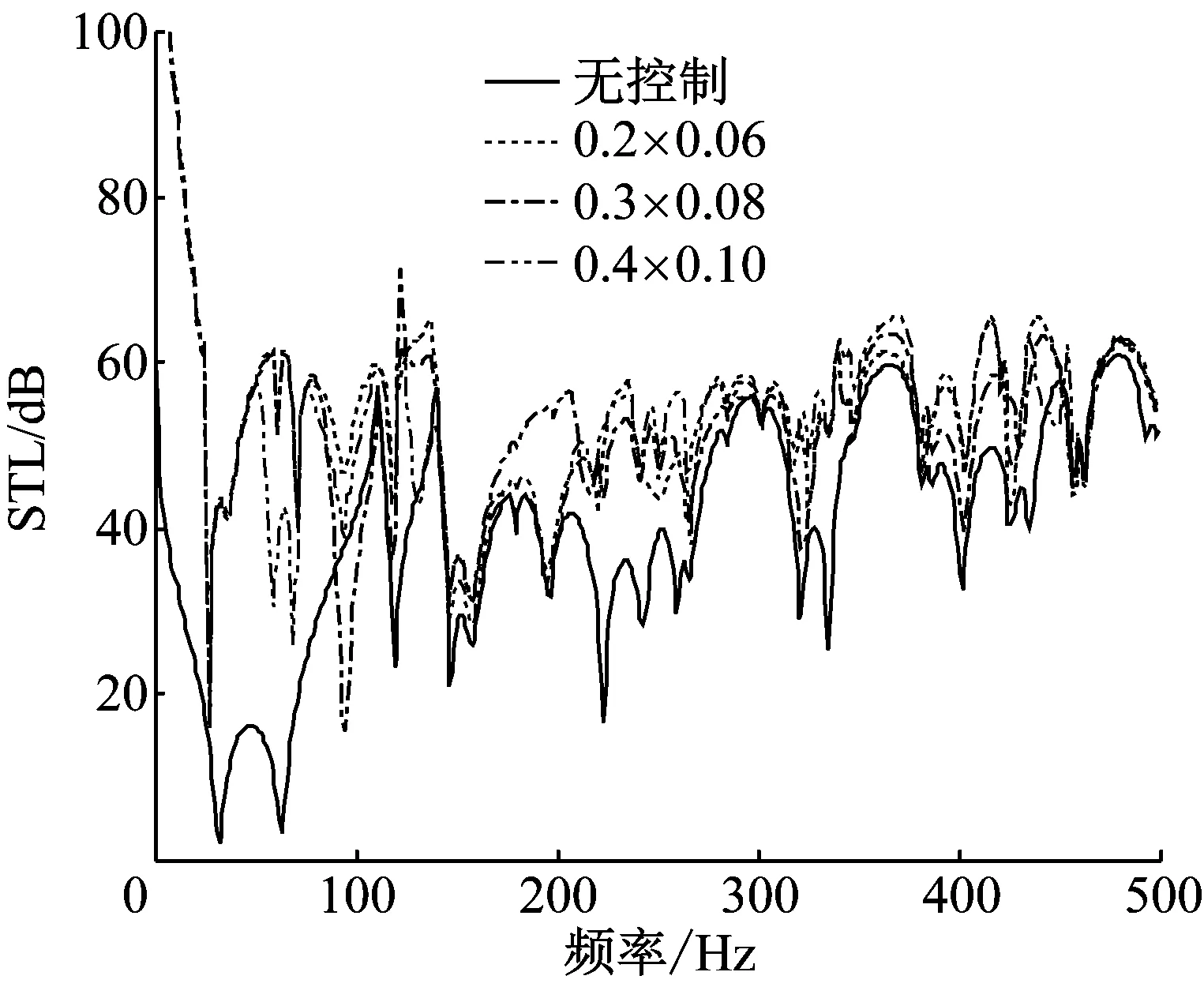
(b) 以夹层声功率最小化为控制目标

Fig.9 Effects of the size of the panels acted as the active acoustical boundary on STL of simply supported double-panel systems with different control objectives

图10(a)和图10(b)分别为以辐射声功率最小和以夹层声功率最小化为控制目标，采用不同尺寸的控制边界，在控制前后辐射面板的振动动能曲线。如前所述，从图10(a)和10(b)可以看出，不同尺寸的主动声边界对辐射面板动能的影响与图9中传声损失的影响基本相同，随频率表现出相同的变化过程。

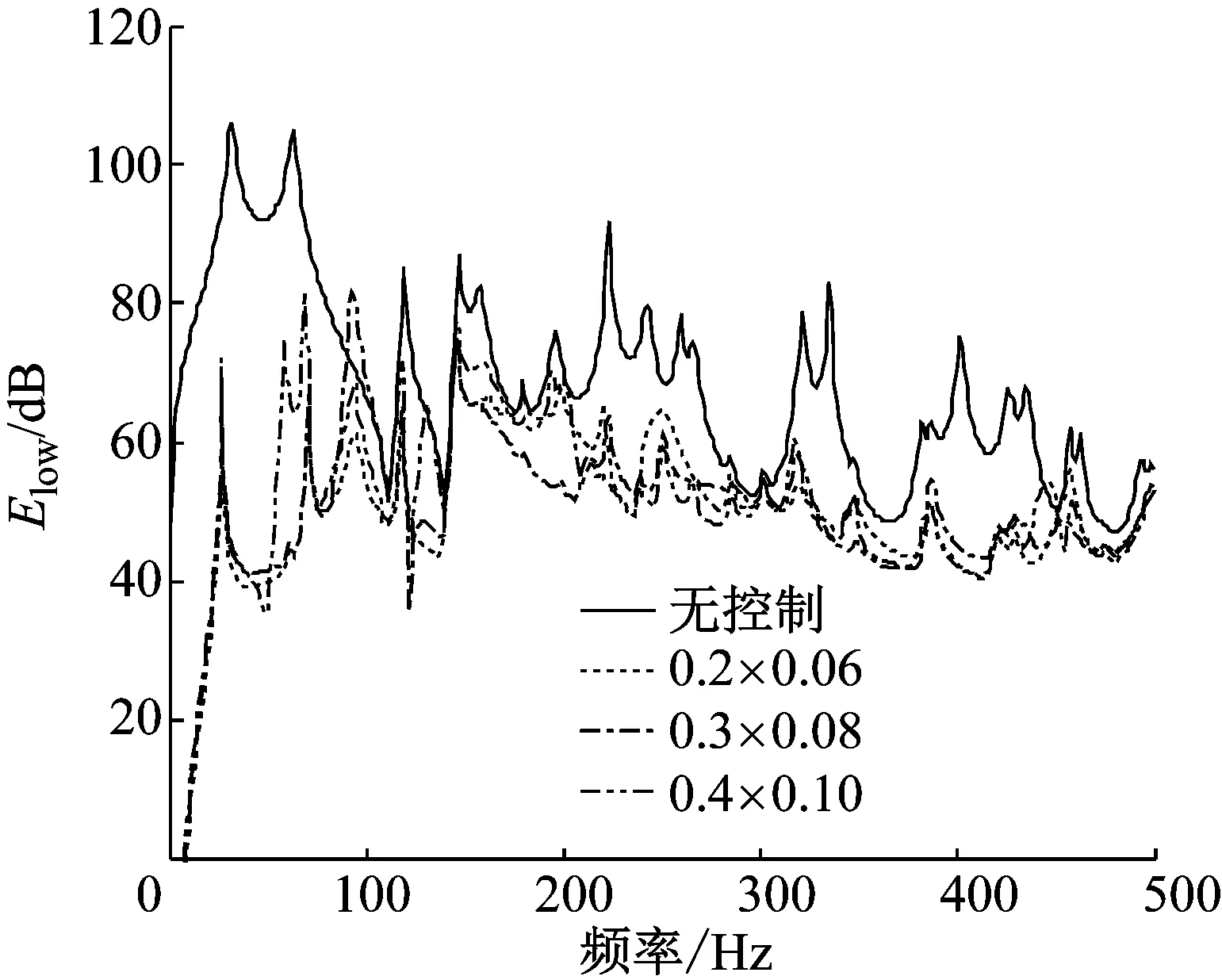
(a) 以辐射声功率最小为控制目标

(b) 以夹层声功率最小化为控制目标

Fig.10 Effects of the size of the panel acted as the active acoustical boundary on averaged kinetic energy of the lower panel for simply supported double-panel systems with different control objectives

图11(a)和图11(b)分别为以辐射声功率最小和以夹层声功率最小化为控制目标，采用不同尺寸的控制边界，控制前后夹层声场的声功率变化曲线。首先，从图4和图11中可以看出，对于相同尺寸的主动声边界，采用不同控制目标，在控制后获得的夹层声场的声功率差别不大；而对于相同控制目标，不同主动声边界尺寸，在控制后对不同频率区间内夹层声场声功率影响不同。在小于50 Hz和大于300 Hz的频率区间，控制后三种尺寸主动声边界板对夹层声场声功率的影响基本相同；在50～300 Hz之间的频率段，与图10类似，虽都一定程度提高了夹层结构的隔声性能，但结构尺寸的影响并没有表现出一定的规律。

图12(a)和图12(b)为以辐射声功率最小和以夹层声功率最小化为控制目标，采用不同尺寸的控制边界，控制后左侧主动声边界板的平均振动动能的变化曲线。从图中可以看出在控制实施后，不同尺寸的主动声边界板的动力学响应有很大的差异。如前所述，图中曲线出现的尖峰与控制后的双层板系统中各子系统的能量曲线上出现的尖峰对应。

(a) 以辐射声功率最小为控制目标

(b) 以夹层声功率最小化为控制目标

Fig.11 Effects of the size of panel acted as the active acoustical boundary on sound power of the gap sound filed for simply supported double-panel systems with different control objectives

总之，仿真计算过程中只有主动声边界板的尺寸在变化，对于不同尺寸的主动声边界板，图9～图12中不同曲线的差异反映了主动声边界尺寸对双层板系统隔声性能和各子系统响应的影响。对于低频率段，由于声波波长远大于结构尺寸，声场声压几乎均匀分布，因此不同尺寸主动声边界对夹层结构的隔声性能提高的程度相同。对于其他频率段，对于子系统各部分响应的影响并没有一定的规律。从上面的分析可以看出，不同频率不同尺寸的主动声边界，对夹层结构隔声性能的影响不尽相同，且主动声边界有一定的可设计性，因此，为了改善双层板系统的隔声性能，可以对主动声边界的尺寸进行优化设计，达到提高隔声性能的目的。

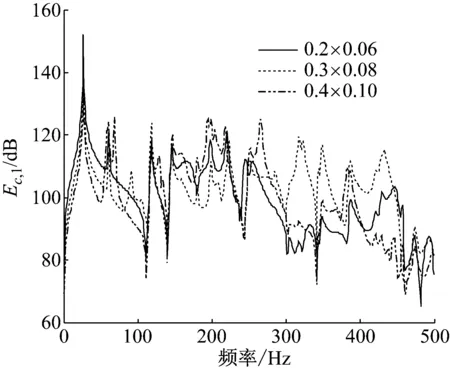
(a) 以辐射声功率最小为控制目标

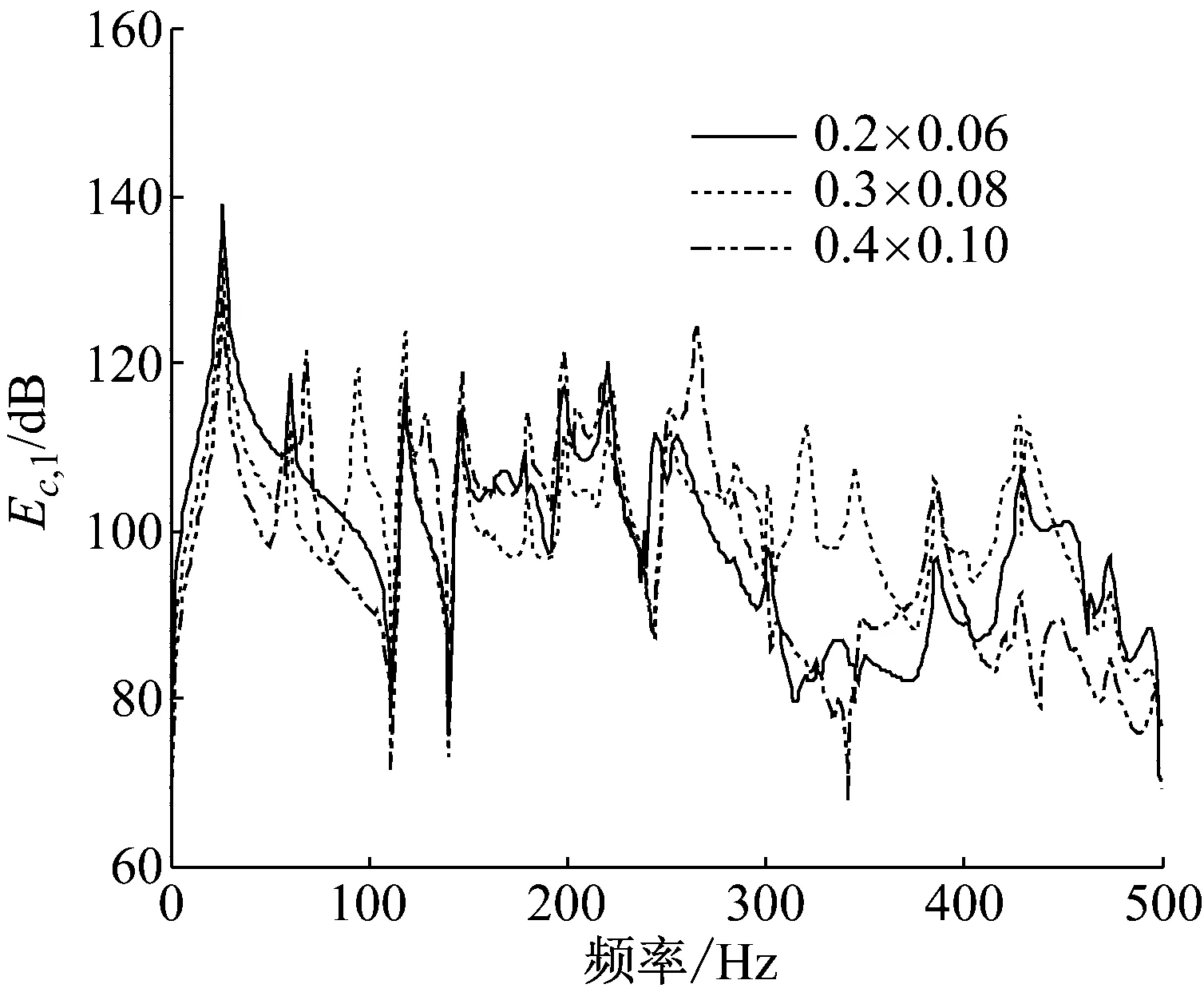
(b) 以夹层声功率最小化为控制目标

Fig.12 Effects of the size of the panel acted as the active acoustical boundary on averaged kinetic energy of the left panel for simply supported double-panel systems with different control objectives

4 结 论

本文提出基于主动声学边界方法的有源隔声夹层结构。首先，建立了基于主动声学边界的双层板有源隔声结构计算模型，即在双层板结构的空气夹层边界上布置主动声学边界，文中采用四边简支板代替主动声边界，并在其上作用次级控制力，采用声弹性理论导出各子系统之间的耦合关系，分别以辐射声功率最小和以夹层声场的声功率最小作为控制目标求取最优控制力。通过计算分析获得以下结论：主动声边界控制策略可以有效提高双层板结构的隔声性能，特别是低频段的隔声新能；为提高夹层结构的隔声性能，以辐射声功率最小作为控制目标要优于以夹层声场的声功率最小为控制目标；控制后，主动声边界对入射板振动响应几乎没有影响，辐射面板的振动动能和夹层声场的声功率均被有效地抑制，辐射面板振动模态与夹层声场模态以及主动声边界板振动模态与夹层声场模态之间的相互耦合改变夹层声场声压分布，改变辐射面板的振动情况，降低向辐射声场辐射声波。同时，对主动声边界板的尺寸对隔声性能和各子系统响应的影响的研究表明：不同尺寸主动声边界都提高了夹层结构的隔声性能；对于低频率段，不同尺寸主动声边界对夹层结构的隔声性能提高的程度相同；对于其他频率段，主动声边界对各子系统响应的影响并没有一定的规律；不同频率不同尺寸的主动声边界，对夹层结构隔声性能的影响不尽相同，由于主动声边界有一定的可设计性，因此可以对主动声边界的尺寸进行优化设计，达到特定频段隔声性能有所提高的目的。

[1] 杜功焕，朱哲民，龚秀芬. 声学基础[M].南京：南京大学出版社，2009.

[2] XIN F X, LU T J, CHEN C Q. Sound transmission through simply supported finite double-panel partitions with enclosed air cavity [J]. Journal of Vibration and Acoustics, 2010, 132(1): 011008: 11001-11011.

[3] 陈克安. 有源噪声控制[M].北京：国防工业出版社，2014.

[4] PAN J, SYNDER S D, HANSEN C H, et al. Active control of far-field sound radiated by a rectangular panela general analysis [J]. Journal of the Acoustical Society of America, 1992, 91: 2056-2066.

[5] LEE J C, CHEN J C. Active control of sound radiation from a rectangular plate excited by a line moment [J]. Journal of Sound and Vibration, 1999, 220(1): 99-115

[6] PAN J, BIES D A. The effect of fluid-structural coupling on sound waves in an enclosure: Theoretical part [J]. Journal of the Acoustical Society of America, 1990, 87(2): 691-707.

[7] PAN J, HANSEN C H, BIES D A. Active control of noise transmission through a panel into a cavity- I. Analytical study [J]. Journal of the Acoustical Society of America, 1990, 87(5): 2098-2108.

[8] KIM S M, BRENNAN M J. Active control of harmonic sound transmission into an acoustic enclosure using both structural and acoustic actuators [J]. Journal of the Acoustical Society of America, 2000, 107(5): 32523-2534.

[9] PAN J, BAO C. Analytical study of different approaches for active control of sound transmission through double walls [J]. Journal of the Acoustical Society of America, 1998, 103(4): 1916-1922.

[10] CARNEAL J P, FULLER C R. An analytical and experimental investigation of active structural acoustic control of noise transmission through double panel systems [J]. Journal of Sound and Vibration, 2004, 272(3/4/5): 749-771.

[11] 靳国永，张洪田，刘志刚，等. 基于声辐射模态的双层板声传输有源控制数值仿真和分析研究[J]. 振动工程学报，2011, 24(4): 435-443.

JIN Guoyong, ZHANG Hongtian, LIU Zhigang, et al. Numerical analysis of active control of sound transmission through a double-panel structure by using radiation modes [J]. Journal of Vibration Engineering, 2011, 24(4): 435-443.

[12] LI Y Y, CHENG L. Mechanisms of active control of sound transmission through a linked double-wall system into an acoustic cavity[J]. Applied Acoustics, 2008, 69: 614-623.

[13] PIETRZKO S J, MAO Q. New results in active and passive control of sound transmission through double wall structures [J]. Aerospace Science and Technology, 2008, 12(1): 42-53.

[14] DOWELL E H, GORMAN G G, SMITH D A. Acoustoelasticity： General theory, acoustic natural modes and forced response to sinusoidal excitation, including comparisons with experiment [J]. Journal of Sound and Vibration, 1977, 52(4): 519-542.

[15] 靳国永，刘志刚，杨铁军. 双层板腔结构声辐射及其有源控制研究[J]. 声学学报，2010, 35(6): 665-677.

JIN Guoyong, LIU Zhigang, YANG Tiejun. An analytical investigation of active control of sound transmission through double panel-cavity system[J]. ACTA Acoustic, 2010, 35(6): 665-677.

Activedouble-panelsoundinsulationstructurebasedontheactiveacousticalboundaryactingontheboundariesofairgapsoundfield

NINGShaowu1,SHIZhiyu1,XUXinyin2

(1. State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China; 2. Institute of Systems Engineering, China Academy of Engineering Physics, Mianyang 621900, China)

Based on the active acoustical boundary method, an active double-panel sound insulation structure was presented, which consists of a double-panel structure and an active acoustical boundary arranged on the boundary of the air gap sound field. Simply supported panels were used to replace the active acoustical boundary and were acted by control forces. In the light of the acoustoelsticity theory, an analytical model was developed to calculate the optimal control forces, considering the minimum radiation sound power and minimum air gap sound power as the control targets. On the basis of the developed theoretical model, the sound transmission loss (STL) and responses of the subsystems of the active double-panel sound insulation structure were studied before and after control. Meanwhile, the effect of the dimensions of the active acoustical boundary on STL and responses of the subsystems were taken into account. The simulations carried out show that the active acoustical boundary control strategy can effectively improve the sound insulation performance of double-panel structures and the better control effect can be gotten with the target of minimum radiation sound power than that with the target of minimum air gap sound power. The active acoustical boundary has no influence on the vibration responses of the upper panel whilst the vibration responses of the lower panel and the air gap sound power are suppressed effectively. The active acoustical boundaries with different dimensions can all improve the sound insulation performance. Especially, in low frequency range, the same insulation performance can be gotten for the different dimensions, but in high frequency, range, the effect of the dimensions of active acoustical boundaries on the STL and responses of subsystems has no definite regularity, so the dimensions of the active acoustical boundaries can be optimized to improve the insulation performance in certain specific frequency ranges.

active acoustical boundary method; acoustoelsticity theory; sound transmission loss; active double-panel sound insulation structure; radiation sound power

TB535

A

10.13465/j.cnki.jvs.2017.21.030

江苏省普通高校研究生科研创新计划资助项目(CXZZ13_0147); 2015年度省产学研前瞻联合研究项目(BY2015003-01)；机械结构力学及控制国家重点实验室(南京航空航天大学)自主研究课题资助(0515G01)；国家自然基金(11172131; 11232007)；中央高校基本科研业务费专项资金资助; 江苏高校优势学科建设工程资助项目

2016-05-31 修改稿收到日期：2016-07-13

宁少武 男，博士生,1985年生

史治宇 男，教授，博士生导师，1967年生。E-mail: zyshi@nuaa.edu.cn