机械信号时域平均消噪方法的滤波器实现

冯武卫， 李鹏鹏， 张玉莲， 施立峰

(1. 浙江海洋大学 船舶与海洋工程学院， 浙江 舟山 316022； 2. 浙江省近海海洋工程技术重点实验室， 浙江 舟山 316022； 3. 浙江金鹰集团股份公司， 浙江 舟山 316101)

机械信号时域平均消噪方法的滤波器实现

冯武卫1，2， 李鹏鹏1， 张玉莲1， 施立峰3

(1. 浙江海洋大学 船舶与海洋工程学院， 浙江 舟山 316022； 2. 浙江省近海海洋工程技术重点实验室， 浙江 舟山 316022； 3. 浙江金鹰集团股份公司， 浙江 舟山 316101)

时域平均法是故障诊断中常用的非常有效的信号处理方法，主要特点是可以从混有噪声干扰的信号中提取感兴趣的周期性信号，同时抑制不相关的其它周期成份。然而时域平均存在两方面明显的不足：一方面，键相信号的拾取常受到应用环境和条件的制约难以实施，即便获得键相信号，也往往由于周期截断误差的存在使时域平均方法不能取得满意的效果；另一方面，时域平均要求大量数据的存储、运算，这给时域平均的应用也带来一定的不便。为了解决上述问题，本文根据时域平均的幅频特性提出采用FIR多带滤波器实现时域平均功能的方法，该法有效避免了传统方法需采集键相信号的不足，很好的扩大了时域平均在实际工程中的应用。最后，将传统的时域平均方法和利用多带滤波器实现时域平均功能的方法进行了分析比较，验证了本文方法的有效性。

时域平均方法； 多功能滤波； 故障诊断系统

时域平均技术有其独特的优势，可在强噪声条件下使用，可以有效提高信号信噪比，提取淹没在噪声中的有用分量，消除与给定信号频率无关的成分[1]。时域平均法是一种有效的在时域统计处理的分析方法，近年来众多学者对该方法的研究愈演愈烈。然而，时域平均方法存在键相信号难以获取、处理精度不高等问题，针对上述方法存在的不足，国内外该领域专家做了大量研究工作[2-5]。

刘红星为了减小周期截断误差，提出了一种新算法，克服了累积周期截断误差对有用信号分量的衰减，取得了良好的效果[6]。 McFadden等[7]将插值技术应用于齿轮故障诊断的时域平均消噪处理中，提高了时域平均的处理精度，取得了较好的效果。余建航等[8]发表了一篇关于周期测量误差对周期信号时域平均处理结果的影响的论文，该论文对测量误差对精度的影响做了深入研究，给出了时域平均处理后信号各阶简谐分量幅值衰减量和相位变化与周期测量误差、平均次数以及分量阶次之间的关系式，对该方法的工程应用具有重要的指导意义。 Combet等[9-10]研究了时域平均的相位差校正技术，对齿轮箱中故障检测具有积极的推动作用。刘中栋等[11]在时域平均对高次谐波影响的研究中提出加窗优化的方法，进而提高了时域平均在处理次谐波的精度。朱利民等[12]深入探讨了不经过任何外部参数设定的时域平均技术，并取得了阶段性的成果。此外，William等[13-14]在时域平均方法研究方面也取得了一些显著的成果。

综上，尽管国内外的研究工作从不同方面提高了时域平均的分析效果。但不难发现，多数研究仅仅是基于传统方法的改进，如果键相信号已获取，上述各种方法结果都将产生良好的应用价值；但在复杂、条件恶劣的环境下，键相信号获取往往非常困难，因此，上述方法的应用范围得到一定的制约。本文提出了一种时域平均方法的滤波器实现技术，此技术无需键相信号，通过对本文方法的仿真和实验分析，其效果可以达到工程应用的精度，证明了本文方法的有效性。

1 本文方法研究思路

时域平均原理的说明在罗德扬的研究中有详细的介绍，此处不在赘述。为了进一步了解时域平均的内涵，本文首先就时域平均的幅频图做深入分析，由时域平均公式通过一系列变换所得对应的幅频响应函数如下所示，其中幅频曲线如图1所示。

幅值为：

(1)

相位为：

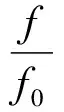
(2)

不难发现，当取不同叠加段数N时，对应的时域平局幅频特性是不同的，我们可以通过这些曲线变化规律来研究时域平均方法的本质。由式(1)、(2)知，当我们取不同的段数N(N=8，N=16及基频f0=50 Hz)，所得到幅频图见图1。

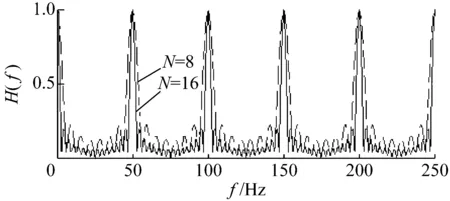
图1 时域平均幅频响应

从图1可知，时域平均幅频图相应曲线是由一系列的等距分布的带通梳状曲线及旁瓣组成，随着叠加段数N的增大，梳状曲线越陡峭，且旁瓣越窄，这也就是时域同步平均能有效提取与回转频率相关的周期信号，且对噪声及非相关信号成分具有较强的压制能力的原因。基于时域平均的幅值响应图形特点，即时域平均方法提取周期分量的过程，可以看作是对信号进行滤波的过程。

实际上，信号消噪方法有很多种，如小波分析、经验模式分解等。小波分析(wavelet,WV)的地位在信号处理中优势较为明显，尤其是谐波小波，谐波小波理论上讲是理想的带通滤波器，这由从小波的“盒形频谱可以推知。然而小波基函数较难确定，且小波是一种持续一分为二的分频段处理过程，因此，采用小波滤波来实现时域平均功能无法实现。其它信号处理方法如经验模式分解(Empirical Mode Decomposition, EMD)，其重点处理非平稳信号，忽略了相位信息，因此同样不适合此处的方法。其次， 采用EMD方法，分解过程数据两端将产生“端点效应”问题，并且这种效应会逐渐向内“污染”整个数据序列而使所得分解结果严重失真。

综上所述，小波分析及经验模式分解在某些领域取得了不错的效果，但对于时域平均功能的实现，都显得无能为力。它们的滤波特性都是在信号中提取某频率信号而不是消除信号的其他信号的过程，只有多带滤波的效果与时域平均的出发点是一致的，因此，本论文后续部分将重点讨论时域平均滤波器如何实现的问题。

2 时域平局滤波器的选择与构造

2.1滤波器的选择

选择何种滤波器对时域平均功能的实现非常重要。滤波器的种类非常繁多，其中数字滤波器的应用变得越来越广泛，数字滤波器主要分为两种：即有限冲激响应滤波器(Finite Impulse Response, FIR)和无限冲激响应滤波器(Infinite Impulse Response, IIR)。FIR滤波器的最大优点是可具有线性相位且系统结构始终稳定，还可以实现零相移滤波。为了获得较好的滤波特性曲线，往往滤波阶次选取较大，因此，FIR滤波器的缺点是滤波时的计算量相对较大，信号处理的实时性很难达到，在对信号实时性要求较高场合不易选用，该类型滤波器的设计方法也有很多，典型的如窗函数法、频率抽样法和切比雪夫最佳一致逼近法，如果对相位要求很高且计算速度容许的条件下，FIR滤波器是很好的选择。IIR滤波器的最大优点是可以得到准确的通带和阻带边缘频率，可取得非常好的通带和阻带衰减，但缺点是系统存在稳定性问题，另一方面对处理的信号不能保证线性相位关系。通过比较并结合时域平均的具体要求，由于时域平均对相位要求较高，因此，选择FIR多带滤波器来实现时域平均功能。

2.2滤波器的构造

为保证特定周期成分的基频和其倍频之间无相移，本文采用线性相移且系统始终稳定的有限冲击响应(FIR)数字滤波技术设计零相移带通滤波器。其设计过程如下：

1) 确定多带滤波器的理想频率特性Hd(f)

多带滤波器需要保留基频及其倍频周围的频率，即f0及kf0为中心频率，两侧分别±P作通带(根据需要进行确定)，因此其理想频率特性为：

(3)

其理想状态下Hd(f)的频率特性如图2所示。

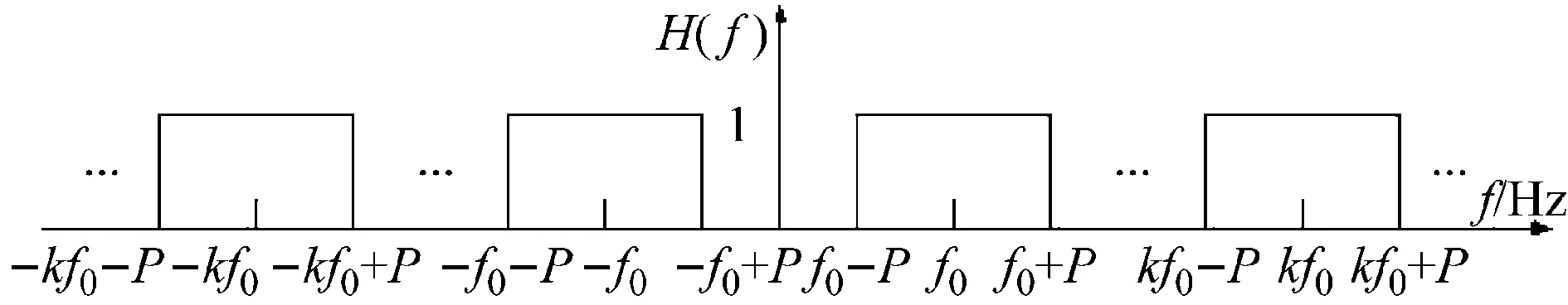
图2 理想多带滤波器频率特性

2) 求单位取样响应：

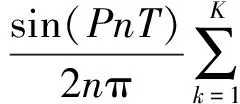
(4)

式中：K为多带滤波器通带的个数；T为采样周期；f0为基频。

3) 窗函数选择

在保证阻带衰减满足要求的情况下，窗函数尽量选择主瓣窄、边瓣峰值小的函数。和矩形窗相比，汉明窗和汉宁窗主瓣稍宽，但有较小的旁瓣和较大的衰减速度，较为常用。此处本文选择汉宁窗作为窗函数。

(5)

4) 求单位冲击响应

h(n)=hd(n)ω(n)

(6)

即

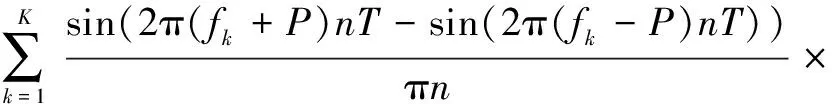
(1+cos(πn/N))

(7)

式中：P为通道的半带宽；N为滤波器阶数。

式中fk由式(6)得到，经过上述4个步骤，构造的多带滤波器的单位冲击响应h(n)及其频率特性如图3所示(其中选择N=400，K=7)，K的选择应为：K倍f0小于fs/2。

(a) 冲击响应

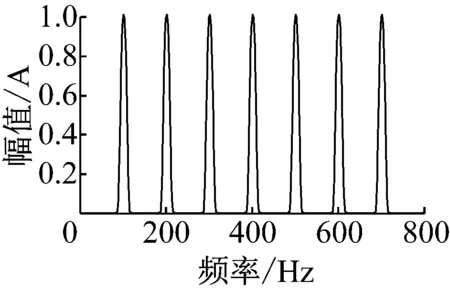
(b) 频率特性

3 仿真及实验信号分析

3.1仿真信号分析

本文仿真的是齿轮齿面损伤信号，当齿轮的齿面产生均匀磨损而使得齿隙增大时，或齿面上有裂痕、点蚀、剥落等损伤时，会产生冲击振动，并激发齿轮按其固有频率振动，在频率成分中产生啮合频率的2次、3次等高次谐波或1/2、1/3等的分频成分。

设仿真信号由周期信号和随机白噪声组成。形如：

x(n)=sin(2πfmnT)+0.2sin(4πfmnT)+

0.33sin(6πfmnT)+0.1sin(8πfmnT)+sin(2πf1nT)+sin(2πf2nT)+0.4sin(2πf3nT)+r(n)

(8)

式中:信号是由基频f0=fm=50 Hz(啮合频率)及其倍频2fm、3fm、4fm与频率为f1、f2和f3的正弦信号及白噪声r(n)叠加而成，其中f1、f2和f3作为干扰信号的频率，与基频不成倍数关系。采样频率fs=1 000 Hz；干扰信号频率f1=33 Hz，f2=133 Hz，f3=233 Hz；采样点数为100。信号的波形及其频谱如图4(a)所示。在此设定多带滤波器的参数为：M=400，通带的半带宽P=8，通带的个数K=4。仿真信号x(n)经过多带滤波器处理后的波形和频谱如图4(b)所示。

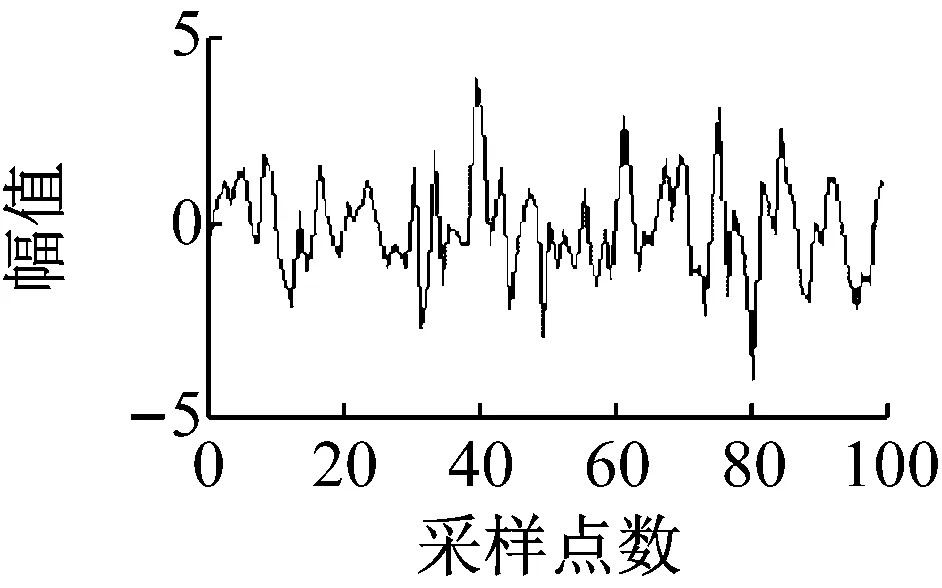
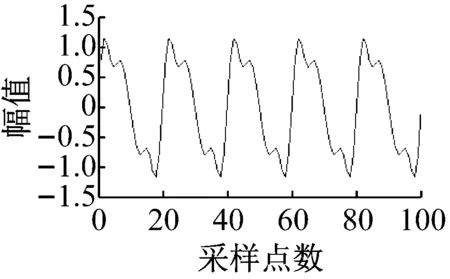
3.2实测齿轮信号分析

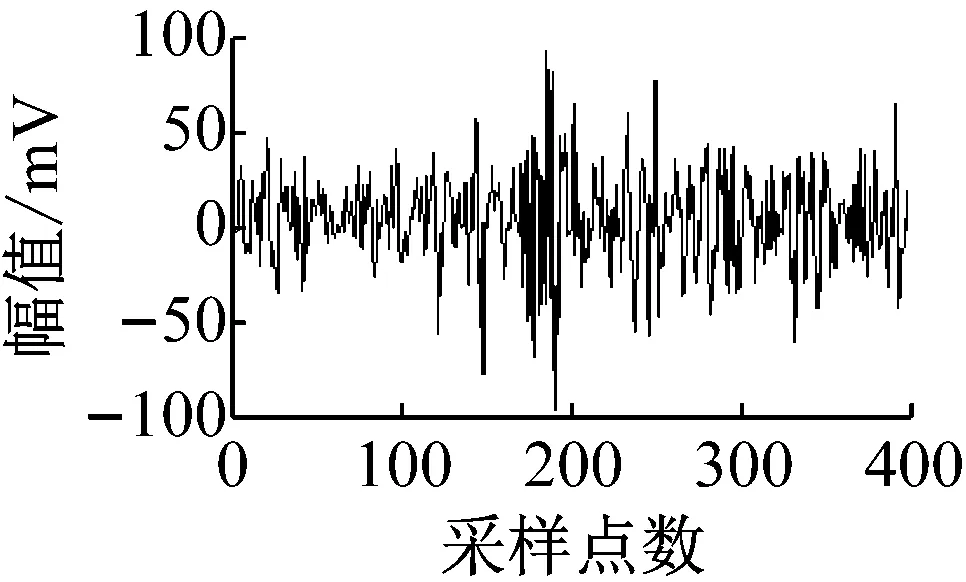
图5(a)所示为某齿轮故障模拟实验台上采集的一组振动信号。信号参数为：输入轴转速为800 r/min，采样频率为5 120 Hz,采样点数为16 384，大约为40个整周期，齿轮啮合副为26/64，此处取第一段信号400个采样点进行分析(总点数为16 384，传统时域平均方法一共截取40段，每段400个点)，通过前述多带滤波器的设计及中心频率的选择，滤波结果如图5(b)所示。

由图5可知，该方法很好的消除了噪声及不感兴趣的信号成分，提高了信号的信噪比，达到了很好的预期效果。图5(a)可见，对原先噪声干扰严重的波形信号，经处理后，所得波形可以明显的反映齿轮运行的时域特征，可以清楚的分辨出26个间隔基本相等的冲击信号，对应输入轴上齿轮的齿数，从各个冲击的幅值看出，呈现出一个由小到大又变小的过程，由此看出，齿轮运行并不正常，可能存在弯曲或偏心问题；从图5(b)频谱图也可看出，处理后的信号频谱接近与理想状态下的时域平均结果，使不相关的频谱成分完全得以压制。同时具有时域平均对信号具有选择性分析的优点，只要设定自己感兴趣的频带成分，选取不同的K值即可。

为了比较该方法与传统方法的分析效果，同样采用上述齿轮信号，采用传统的分段重采样来进行同步校正、然后进行叠加平均，所截段数为40段，用两种方法对其处理，得到时域波形特征基本一致(见图6)，证明了该方法的可行性。

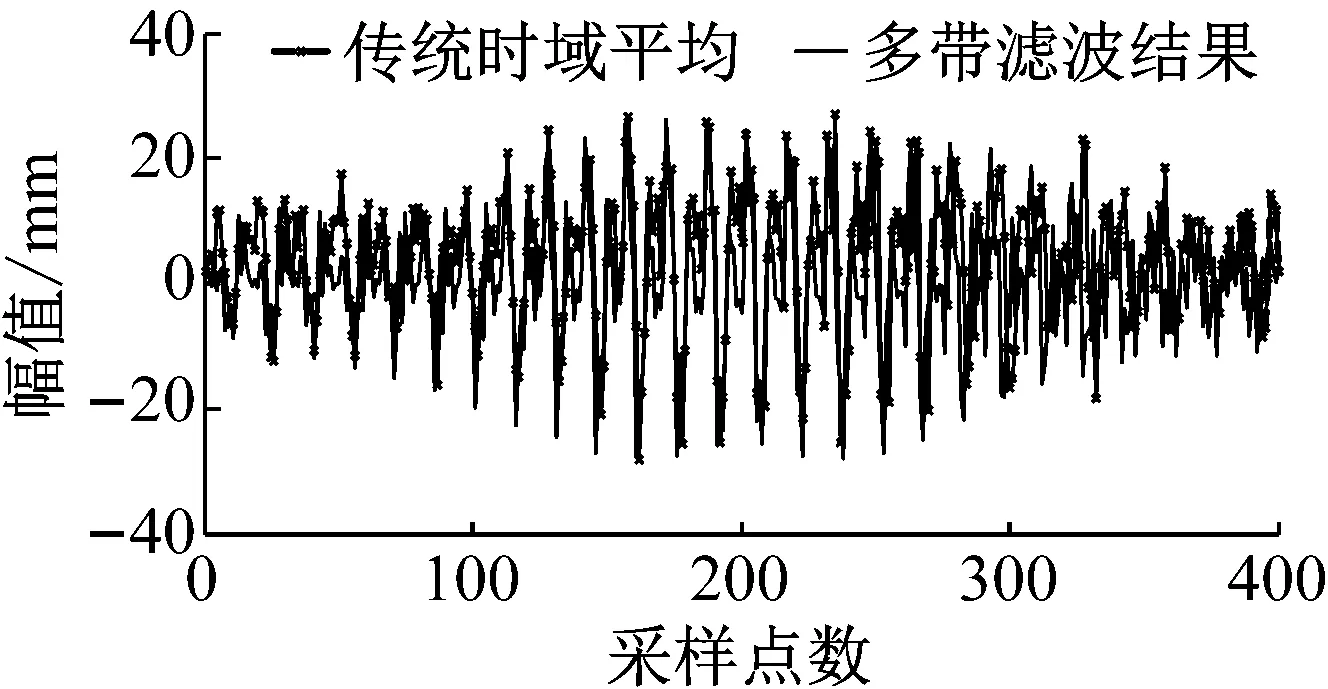
图6 齿轮信号两种方法比较结果

4 结 论

本文在时域平均幅频图特性的基础上提出了用多带滤波器实现时域平均的方法。研究了时域平均滤波器的选择、构造及参数优化问题，通过对仿真信号和实际信号分析处理，其结果验证了该方法的可行性。实验结果表明，该方法可以有效的让感兴趣的周期信号的基频及倍频通过，滤除无关的干扰分量，实现了时域平均的功能，该方法不需获取键相信号的复杂硬件设施，简单方便，应用灵活，数据存储运算少，避免了传统应用时域平均法的不足，有效扩大了时域平均方法的应用范围，是实现时域平均功能的有效方法。

[1] 罗德扬．时域同步平均原理与应用[J]．振动、测试与诊断，1999，19(3):202-207.

LUO Deyang, Time domain average princple and application[J]. Journal of Vibration Test and Diagnosis, 1999, 19(3):202-207.

[2] 吕琛,宋希庚,邹积斌. 基于DSP的振动信号阶比与时域同步平均分析[J]. 振动与冲击,2002,21(2):53-57,98-99.

LÜ Chen, SONG Xigeng, ZOU Jibin, Studing the vibration signal order and time domain synchronous averaging based on DSP[J]. Journal of Vibration and Shock, 2002,21(2):53-57,98-99.

[3] 张西宁,吴婷婷,徐进杰,等. 变转速齿轮箱振动信号监测的无键相时域同步平均方法[J]. 西安交通大学学报,2012,46(6):111-114.

ZHANG Xining,WU Tingting,XU Jinjie,et al. Time domain synchronous averaging method without key phase signal used to variable speed gearbox vibration signal monitoring[J]. Journal of Xi’an Jiaotong University, 2012,46(6):111-114.

[4] 胡贵锋,王细洋. 基于时域同步平均法的行星齿轮振动信号分离技术[J]. 中国机械工程,2013,24(6):787-791.

HU Guifeng, WANG Xiyang, Researching of planetary gear vibration signal separation technology based on time domain synchronous averaging method[J]. China Mechanical Engineering,2013,24(6):787-791.

[5] 肖志松，郑海起．时域平均在行星齿轮箱故障诊断的应用[J]．河北工业大学学报，2003, 32(6):99-102.

XIAO Zhisong, ZHENG Haiqi. The application of time domain average method in fault diagn[J]. Journal of Hebei University of Technology, 2003, 32(6):99-102.

[6] 刘红星，屈梁生．信号时域平均处理中的若干问题探讨[J].振动工程学报,1997，10(4):446-450．

LIU Hongxing, QU Liangsheng. Questions discuss during to process signal time domain average[J]. Journal of Vibration Test and Diagnosis, 1997, 10(4):446-450.

[7] MCFADDEN P D．Interpolation techniques for time domain averaging of gear vibration[J].Mechanical Systems and Signal Processing, 1989, 3(1):87-97．

[8] 余建航，张曾锠．周期测量误差对周期信号时域平均处理结果的影响[J]. 振动工程学报，1999，12(3): 338-342.

YU Jianhang, ZHANG Zengchang. The effect of period testing error to the processing results of time domain average[J]. Journal of Vibration Engineering, 1999, 12(3): 338-342.

[9] COMBET F， GELMAN L．An automated methodology for performing time synchronous averaging of a gearbox signal without speed sensor[J]. Mechanical Systems and Signal Processing, 2007, 21: 2590-2606．

[10] HALIM E B, SHAH S L, ZUO M J, et al．Fault detection of gearbox from vibration signals using time-frequency domain averaging[C].Proceedings of the 2006 american control conference minneapolis，minnesota，USA， 2006: 4430-4435．[11] LIU Z D， HIMMEL J, BONFIG K W.Improved Processing of Harmonics and Interharmonics by Time-Domain Averaging[J].IEEE Transcations on Power Delivery, 2005,10:2370-2379．

[12] ZHU L M， DING H, MEMBER S, et al. Extraction of periodic signal without external reference by time-domain average scanning[J]．IEEE Transactions on Industrial Electronics,2008,11(2):918-927．

[13] MARK W D. Time-synchronous-averaging of gear-meshing-vibration transducer responses for elimination of harmonic contributions from the mating gear and the gear pair[J]. Mechanical Systems and Signal Processing, 2015, 62-63: 21-29.

[14] AHAMED N, PANDYA Y, PAREY A. Spur gear tooth root crack detection using time synchronous averaging under fluctuating speed[J]. Measurement, 2014, 52:1-11.

Timedomainaveragedenoisingmethodformechanicalsignalsbyusingmulti-bandfiltering

FENGWuwei1,2,LIPengpeng1,ZHANGYulian1,SHILifeng3

(1. School of Naval Architecture and Ocean Engineering Zhejiang Ocean University, Zhoushan 316022, China; 2. Key Laboratory of Offshore Engineering Technology of Zhejiang Province, Zhoushan 316022, China; 3. Zhejiang Golden Eagle Group Stock Company, Zhoushan 316101, China)

The TDA is a very useful signal processing method commonly used in mechanical fault diagnosis. It can be used to extract the specific periodic components from noisy signals and at the same time to suppress other periodic components. But the TDA has two questions, on the one hand, the acquisition of key-phase signal is difficult and the treatment processing is usually influenced by both environment and condition factors. On the other hand, it is also difficult to obtain the satisfied results because of the existense of periodic truncation error. In order to solve these questions, a multi-band FIR filtering based TDA method was proposed. In the method, the key-phase signal is not necessary, which avoids effectively the shortage of traditional methods. This makes it suitable to a wider class of engineering applications. The performances of the traditional TDA method and the multi-band FIR filter method were compared and analyzed. The results show the effectiveness of the new method.

time-domain average method (TDA); multi-functional filter; fault diagnosis system

TH201

A

10.13465/j.cnki.jvs.2017.21.028

国家自然科学基金面上项目(51379189)；中央财政支持地方高校发展专项海洋工程装备创新团队；浙江省科技厅重大专项社会发展项目(2013C03031)

2016-05-04 修改稿收到日期：2016-08-23

冯武卫 男，博士，副教授，1980年1月生