基于联邦扩展卡尔曼滤波的结构损伤识别方法

张 纯， 王路丹， 宋固全， 徐昌宏， 廖 群

(南昌大学 建筑工程学院， 南昌 330031)

基于联邦扩展卡尔曼滤波的结构损伤识别方法

张 纯， 王路丹， 宋固全， 徐昌宏， 廖 群

(南昌大学 建筑工程学院， 南昌 330031)

当结构损伤与传感器故障同时存在时，两者的相互影响会导致损伤识别结果的劣化；为此，提出了一种基于联邦扩展卡尔曼滤波的结构损伤识别算法。利用分散化滤波计算量小、滤波精度高的优点，联邦扩展卡尔曼滤波方法能根据正常的传感器信号准确识别结构的损伤位置与程度，具有良好的鲁棒性；同时利用联邦滤波容错性好的特点，能实现对故障信号的自动检测和剔除，并将剩余的正常子系统进行组合，以继续提供准确的损伤识别结果。梁式结构的数值算例及实验分析验证了该算法的有效性及对故障传感器信号的检测隔离能力。

联邦扩展卡尔曼滤波； 损伤识别； 传感器故障； 残差检验法； 分散化滤波

在结构健康监测领域中，基于结构振动信号的系统辨识和损伤识别技术是当前国内外研究的热点。目前，时域内基于模型的损伤识别方法[1-3]主要包括最小二乘估计、扩展卡尔曼滤波、序贯非线性最小二乘方法等。其中，扩展卡尔曼滤波作为一种可用于非线性系统结构参数识别的实时递推算法，近年来被逐步应用于工程结构的参数反演与损伤识别[4-5]，可实现测量信息不完备[6]、系统参数时变[7]等情况下的结构损伤状态反演。然而，这些研究工作均是基于传感器不存在故障、测量数据完全正确(或含白噪声干扰)的前提下进行，相应的结构损伤识别算法不具有传感器故障信号诊断排除能力。

在实际结构健康监测系统的长期使用过程中，传感器常出现信号漂移、性能蜕化、故障或失效的问题。为保证传感器能准确获取测量信息，研究者提出了众多传感器故障检测方法[8]，但绝大部分基于数学模型的诊断方法是以健康的结构模型为基础的。当结构损伤和传感器故障同时出现时，两者之间的相互作用会严重影响各自的诊断效果。特别是在反问题计算不适定性的影响下，基于故障或不够准确测量信号的损伤识别结果会迅速劣化，失去诊断能力。因此，为保证结构健康监测系统的工作性能，迫切需要发展具有自主故障信号诊断和排除能力的损伤识别算法。

随着多传感器数据融合算法的发展，由Carlson[9]提出的联邦卡尔曼滤波器因设计方案灵活，计算量小、容错性好的优点在组合导航领域得到了广泛应用。作为一种分散式滤波方法，联邦滤波算法不仅具有非常高的识别精度，而且能够对各测量子系统进行故障检测，通过分离故障子系统或调整信息分配因子来抑制故障信号，从而保证系统状态的正确跟踪[10]。

本文结合联邦滤波方法的优点，提出了一种适用于结构损伤识别的联邦扩展卡尔曼滤波方法(Federal Extended Kalman Filter method, FEKF)，不仅具有良好的计算效率、识别精度和鲁棒性，还能及时判别和隔离传感器故障信号，保证结构损伤识别结果的精度和稳定性。梁式结构的损伤识别数值算例及实验分析验证了本文方法的有效性以及对故障信号隔离检测能力。

1 基本理论

1.1结构动力学方程

经过有限元离散后，线性动力系统的运动方程可以写为：

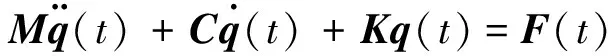
(1)

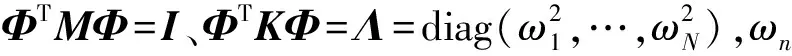
(2)

由于实际结构的自由振动响应可较为方便地通过脉冲激励或自然激励信号得到，因此，文中主要考虑结构的自由振动情况。于是，由式(2)可解得模态坐标的理论解：

pn(t)=e-ξnωntpn0cos(ωdnt)+

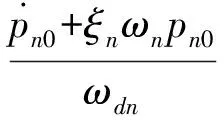
(3)

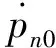
1.2联邦扩展卡尔曼滤波算法

联邦卡尔曼滤波是一种以最小方差为准则的递推估计算法，在对结构参数进行辨识时，可视为一种递推型的模型修正方法。将联邦卡尔曼滤波应用于结构损伤识别时，需要把系统的状态向量进行扩展，通过引入损伤参数来跟踪单元弹性模量的变化规律，从而识别结构损伤。因此，将联邦扩展卡尔曼滤波的系统状态向量定义为：

(4)

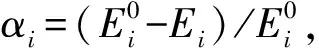
根据联邦滤波器理论框架[10]，它是一种两层结构的分散化滤波器，由若干个子滤波器和一个主滤波器组成。使用时，采用信息分配原理把整个系统中的信息分配到每个局部子滤波器中，利用“方差上界”技术使得每个子滤波器独立工作，然后根据协方差阵把子滤波器的信息进行最优融合估计，得到系统的全局估计值。其结构图如图1所示。

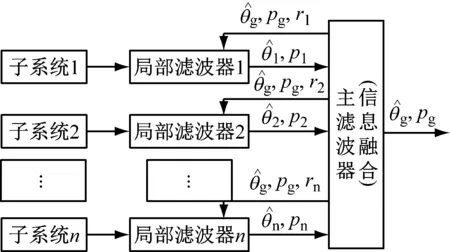
图1 联邦卡尔曼滤波结构图

为解决结构损伤识别问题，本文方法将所有测量传感器进行分组，构成不同的子系统，并采用独立的子滤波器进行参数识别。每个子系统均可形成如下形式的损伤参数估计问题：

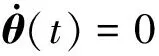
(5)

zi(xi,t)=h(θ,xi,t)+vi

(6)

式中:i代表第i个子系统；相应的观测噪声vi为零均值、协方差矩阵为Ri的高斯白噪声;zi是子系统的观测向量。函数h(θ,xi,t)为子系统测点处的结构振动响应的估计值，根据式(3)，其理论解可表示为

(7)

式中：φn(x)为第n阶的模态向量，x对应观测点的空间坐标。在各子滤波器中，由式(5)、(6)组成的非线性参数识别问题按照传统扩展卡尔曼方法进行递推；再将其识别结果送入主滤波器中进行融合计算，以得到状态向量的最优估计，同时为各子滤波器提供更新后的状态估计值。

根据以上分析，本文建立了基于联邦扩展卡尔曼滤波的结构损伤识别递推算法，其具体流程如下：

(1) 信息分配过程：将主滤波器第k时刻的全局状态估计θg(k)及估计误差协方差矩阵Pg(k)反馈到子滤波器中，以重置子滤波器估计值。具体的信息分配原则为

(8)

θi(k)=θg(k)

(9)

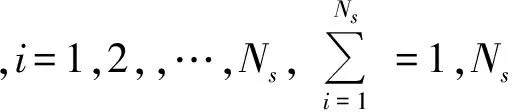
(2) 信息的时间更新：时间更新过程在各子滤波器中独立进行,其中第i个子滤波器的时间更新算法为：

(10)

(11)

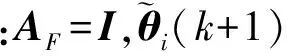
(3) 信息的测量更新：测量更新过程也只在各子滤波器中独立进行

(12)

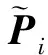
(13)

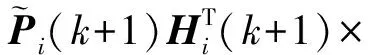
Ri(k+1))-1

(14)

其中因反问题计算的不适定性，式(14)中的矩阵求逆采用了正则化方法[11]。Ki(k+1)为增益矩阵，I为单位矩阵，Hi(k+1)为非线性函数h(θ,xi,t)的雅克比矩阵：

Hi(k+1)=∂h(θi(k+1),xi,tk+1)/∂θi(k+1)

(15)

当结构质量不发生变化时，(15)式计算中所需的固有频率和模态关于损伤参数的灵敏度∂ωn/∂αi、∂φn/∂αi可用基准有限元模型计算[12]。

(4) 信息融合：将各个子滤波器k+1时刻通过时间更新以及测量更新得到的状态向量送入主滤波器中进行融合处理，得到k+1时刻的最优全局状态估计及估计误差协方差矩阵：

(16)

(17)

方程组式(8)～(17)构成了联邦扩展卡尔曼滤波递推过程中的一步，重复以上4个步骤即可完成系统状态向量的最优估计，识别出结构损伤。

1.3基于联邦卡尔曼滤波的传感器故障诊断

随着传感器工作性能的蜕化，测量信号逐步偏离结构的真实动力响应。此时的信号误差与卡尔曼滤波模型中设定的高斯白噪声有明显差异，将导致显著的损伤识别误差。由于联邦扩展卡尔曼滤波是一种分散式滤波，有良好的容错性，故障传感器的影响首先会集中体现在相应的子滤波器中。因此，结合经典的残差χ2检验法[10]，本文方法可以在识别结构损伤的同时，判断测量信号质量，有效诊断、排除故障传感器，保证识别结果的稳定性。

由各子滤波器第k时刻的一步状态预测值和观测值构造出每个子滤波器的新息：

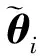
(18)

如果k时刻以前整个系统没有出现故障，各子滤波器新息均为零均值高斯白噪声；当某个传感器发生故障时，相应子滤波器新息将不再满足零均值白噪声条件。因此，根据新息的均值变化即可进行故障检测。

对第i个子滤波器的新息作二元假定：

(1)H0：无故障，

E(ri(k))=0

(2)H1：有故障，

E(ri(k))=μi

E[(ri(k)-μi)(ri(k)-μi)T]=Si(k)

其中Si(k)为ri(k)的方差，根据极大似然比检验原理，可以构建如下故障检测函数:

(19)

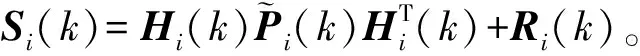
(1) 若λz(k)>TD,判定有故障

(2) 若λz(k)≤TD,判定无故障

其中TD为预先设定的门限，可根据子系统测点数和预先设定的误警率，通过查询χ2分布表得到。于是，利用残差χ2检验法可以检测出各个子系统是否存在故障，然后将各传感器进行不同的子系统组合以确定故障传感器；进而隔离故障信号，避免故障信号对识别结果的干扰。其具体流程如图2所示。

2 数值算例分析

数值算例采用矩形截面的简支梁结构，梁长10 m，截面尺寸为0.25 m×0.5 m，材料弹性模量和密度分别为210 GPa、8 200 kg/m3。简支梁结构被等分为10个梁单元，在第2～10节点上设置传感器，以测量节点竖向位移。同时，根据传感器数量与布置，本文采用了3个子系统，每个子系统包含3个测点，具体的单元划分及测点分配情况如图3所示。

施加任意的初始条件后，将各测点的自由振动信号作为观测值(采样频率设为1 000 Hz)，同时按如下公式加入高斯白噪声模拟观测误差：

zwgn(t)=z(t)+v(t)

(20)

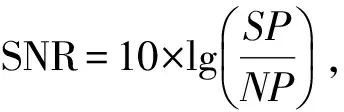
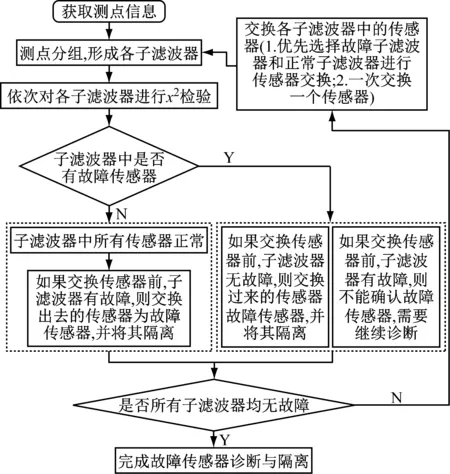
图2 故障传感器诊断与隔离

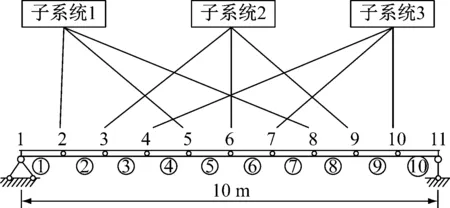
图3 简支梁模型与各子系统测点信号分配

在本文算例中，结构自由振动响应以低阶模态成分为主；理论上在状态变量(4)中保留更多的模态坐标有利于提高计算精度，但也会增加计算负担。因此，本文算法采用前3阶模态坐标来构建状态变量。

2.1单一损伤识别结果

考虑单元5损伤参数为0.3，其它单元无损伤的工况。对于结构响应数据中无噪声、信噪比分别为30 dB、25 dB、20 dB和15 dB的工况，简支梁结构的损伤识别结果如图4所示。尽管输入信号的噪声不断增大，本文方法始终保持很高的损伤识别精度。即使信噪比达到15 dB时，损伤单元弹性模量识别结果的最大相对误差为1.35%。

图5给出了信噪比15 dB时单元损伤参数的识别曲线，初始阶段识别结果波动较大，随后损伤参数快速收敛到实际损伤值，体现出良好的收敛性。

图6给出了测点2的真实信号、加噪信号、滤波信号的结果对比图(为清晰起见，0.25～0.40 s局部时间段的信号如图6(b)所示)。图中，本文算法估计出的测点位移响应信号与真实信号几乎完全重合，滤波效果良好。表1列出了单损工况下状态变量(4)中模态坐标初始值、模态坐标对时间导数的初始值、模态阻尼比系数的识别结果。

图4 不同噪声水平下结构单一损伤的识别结果

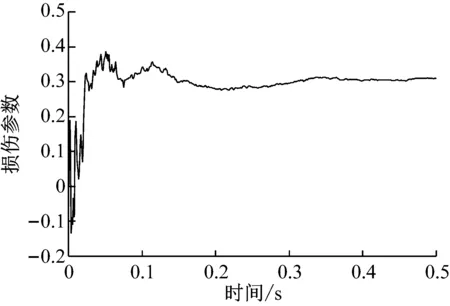
图5 信噪比15 dB时损伤单元参数收敛曲线

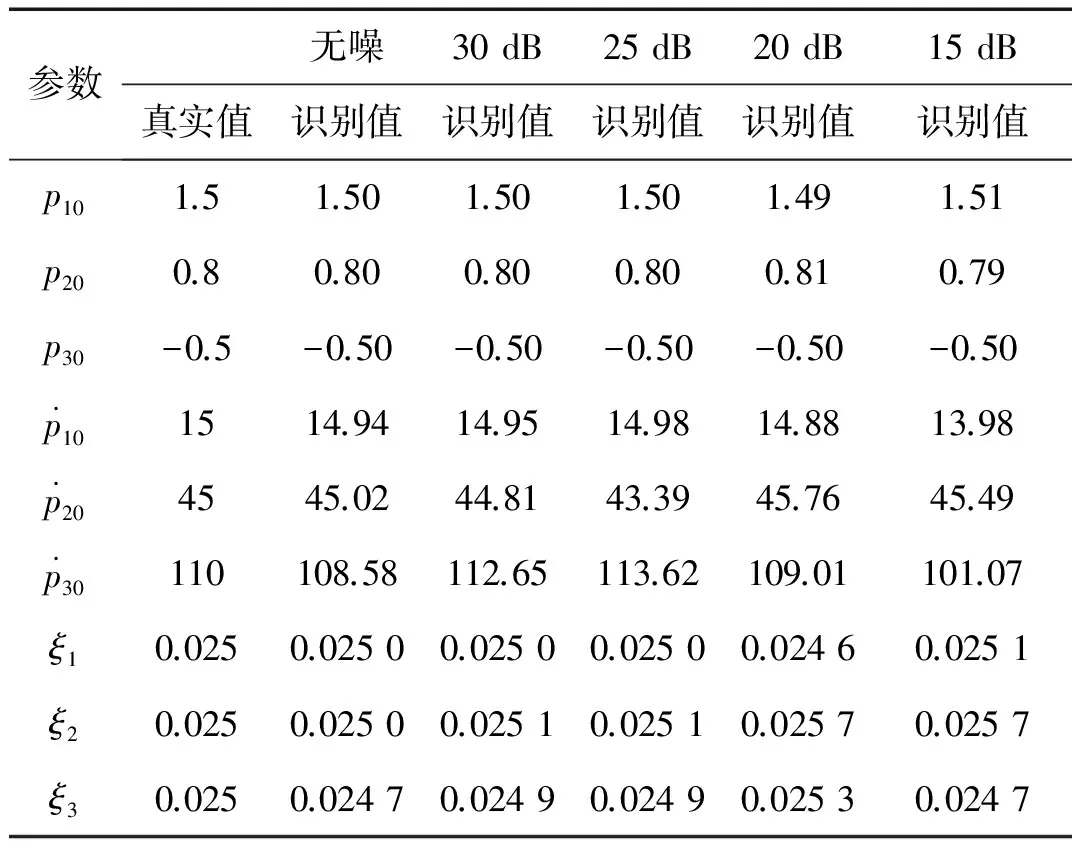
参数无噪30dB25dB20dB15dB真实值识别值识别值识别值识别值识别值p101．51．501．501．501．491．51p200．80．800．800．800．810．79p30-0．5-0．50-0．50-0．50-0．50-0．5p101514．9414．9514．9814．8813．9p204545．0244．8143．3945．7645．4p30110108．58112．65113．62109．01101．07ξ10．0250．02500．02500．02500．02460．0251ξ20．0250．02500．02510．02510．02570．0257ξ30．0250．02470．02490．02490．02530．0247

2.2多处损伤结果识别

设第2、5、8号单元的损伤参数分别为0.4、0.3、0.2，其它单元无损伤。从图7结果可以看出，对于结构多处损伤工况，FEKF方法依然能准确识别损伤的位置与程度。所设置的3处损伤单元弹性模量识别结果的最大相对误差为4.43%，并且随着噪声级别增大，损伤识别结果始终保持很好的精度，体现出算法良好的鲁棒性。从图8及表2给出的结果，可以看出与单一损伤工况的结果类似，即多损工况下测点信号也能跟踪准确，损伤参数也能较快收敛到真值，状态变量的所有元素均能正确识别。

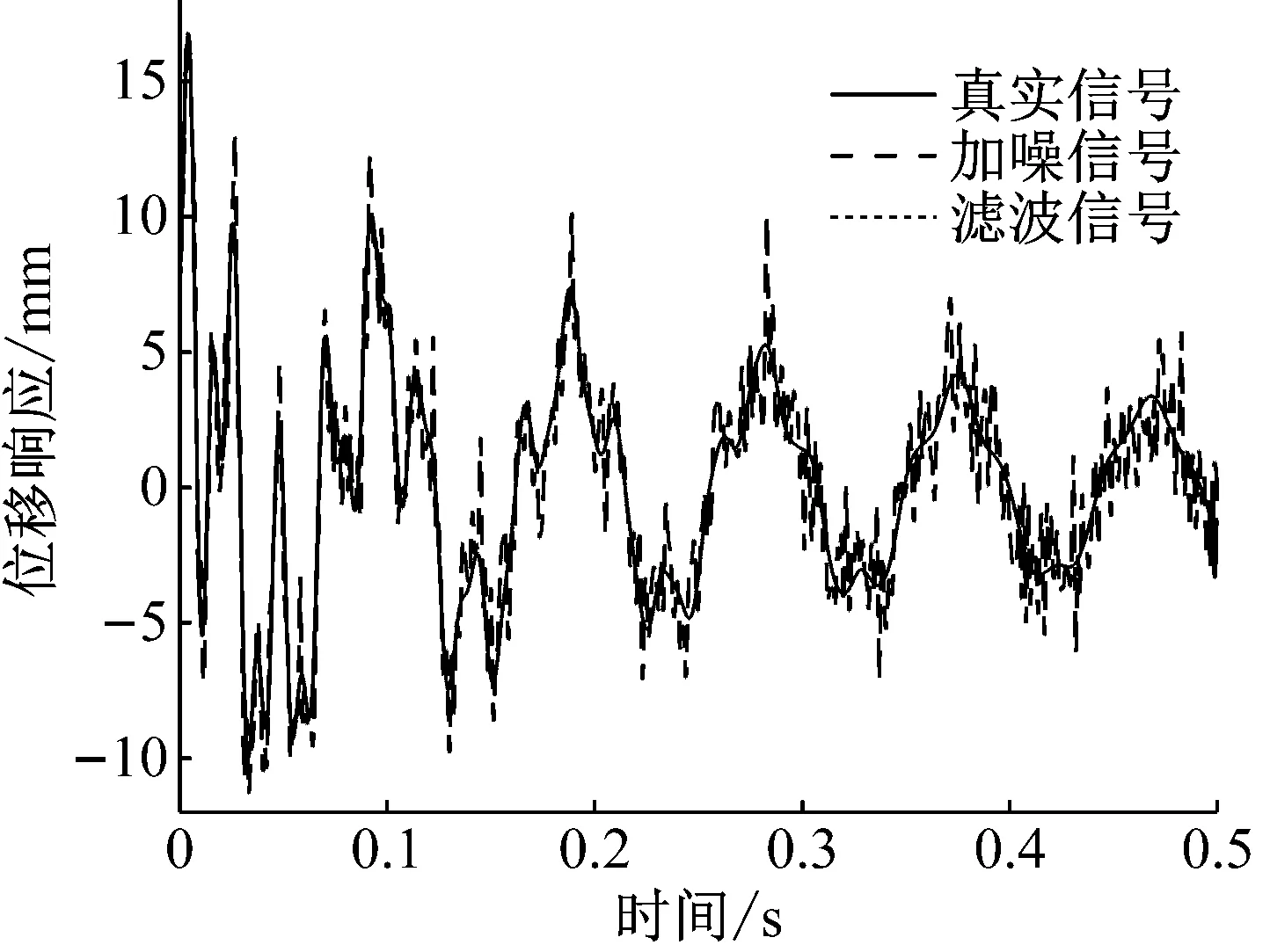
(a)

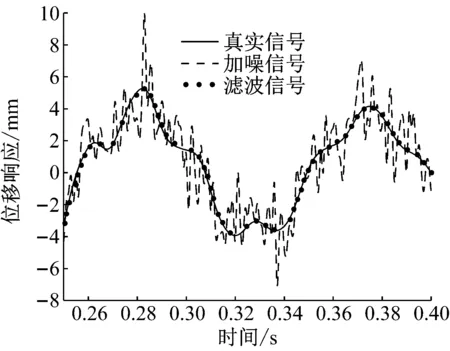
(b)

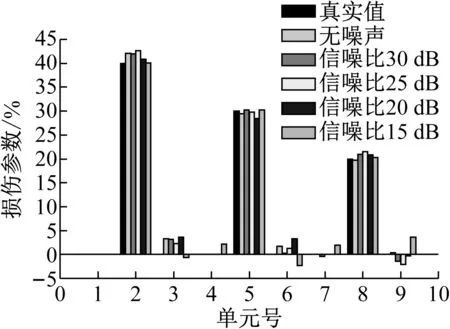
图7 不同噪声水平下结构多处损伤的识别结果

利用表1、表2结果，进一步分析不同噪声级别的影响，可以发现状态向量(4)中各元素识别结果的精度与其对结构响应的贡献密切相关。与损伤参数、模态坐标初始值相比，模态坐标时间导数的初始值对动力响应的贡献会由于阻尼的作用迅速衰减；因此，随着噪声级别的提高，模态坐标时间导数的识别结果会首先劣化；如果噪声级别继续增大，损伤参数、模态坐标初始值的识别误差也会不断增加。总体上，算法在抑制噪声干扰方面具有良好的性能。

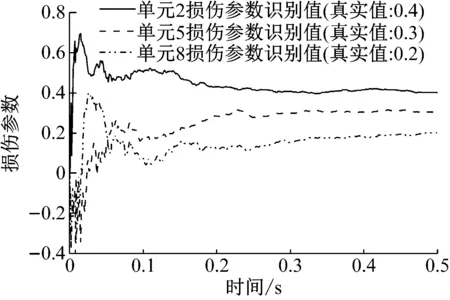
图8 信噪比15 dB时损伤单元参数收敛曲线

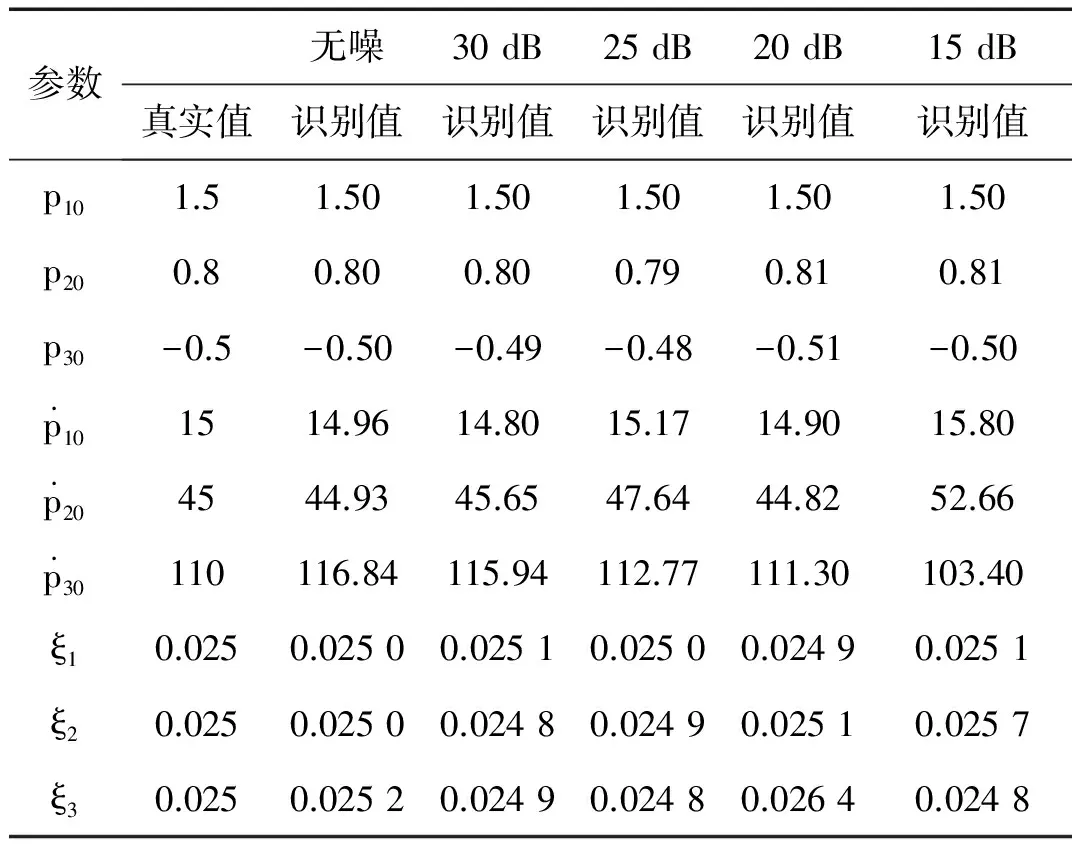
参数无噪30dB25dB20dB15dB真实值识别值识别值识别值识别值识别值p101．51．501．501．501．501．50p200．80．800．800．790．810．81p30-0．5-0．50-0．49-0．48-0．51-0．5p101514．9614．8015．1714．9015．8p204544．9345．6547．6444．8252．6p30110116．84115．94112．77111．30103．40ξ10．0250．02500．02510．02500．02490．0251ξ20．0250．02500．02480．02490．02510．0257ξ30．0250．02520．02490．02480．02640．0248

2.3传感器发生故障的结构损伤识别结果

上述计算结果表明，联邦扩展卡尔曼滤波算法能够准确识别结构的损伤位置与程度，且具有良好的鲁棒性和收敛性。为进一步验证本文方法的故障检测与隔离能力，采用2.2节简支梁结构多损伤工况(信噪比为20 dB)进行分析。受篇幅限制，本文仅考虑突变故障。假设测点5处的传感器发生突变故障(即故障信号与真实信号有一个突变的差值)，导致测点5位移信号从0.05 s开始出现一个大小为0.01 m的突变故障，如图9所示。此时，如果不对故障信号进行检测和排除，图10所示结果表明，损伤识别结果会因测点5的突变故障信号干扰而出现明显的劣化，从而导致损伤误判。

利用联邦扩展卡尔曼滤波方法检测故障信号时，由于每个子系统使用3个测点信息，维数为3，误警率设为0.5%，查χ2分布表可得门限值TD=12.838。根据图2所示的流程，采用残差χ2检验法进行检验：

(1) 由图11(a)所示结果可知，第一个子滤波器的故障检测函数值远大于门限值，表明第一个子系统中存在故障信号；而在图11(b)中第二个子滤波器的故障检测函数值均小于门限值，表明信号正常；第三个子滤波器的现象与第二个子滤波器类似，未单独列出。由此，可判定故障信号来自于第一个子系统，且第二、三子系统中的传感器工作正常，这与算例中的设定是一致的。

(2) 在对各子系统是否存在故障传感器进行判断后，可交换各子系统中的传感器，并根据子系统故障检测函数图的变化，进一步确认故障传感器编号。即将第一个子系统(含故障传感器)的测点2、5、8依次与第二个子系统的测点3进行交换。再利用分别重组的信号重新检验，计算结果显示，当交换测点5与测点3时，第二个子系统出现故障信号，而第一个子系统信号正常，故认为测点5处的传感器为故障传感器。

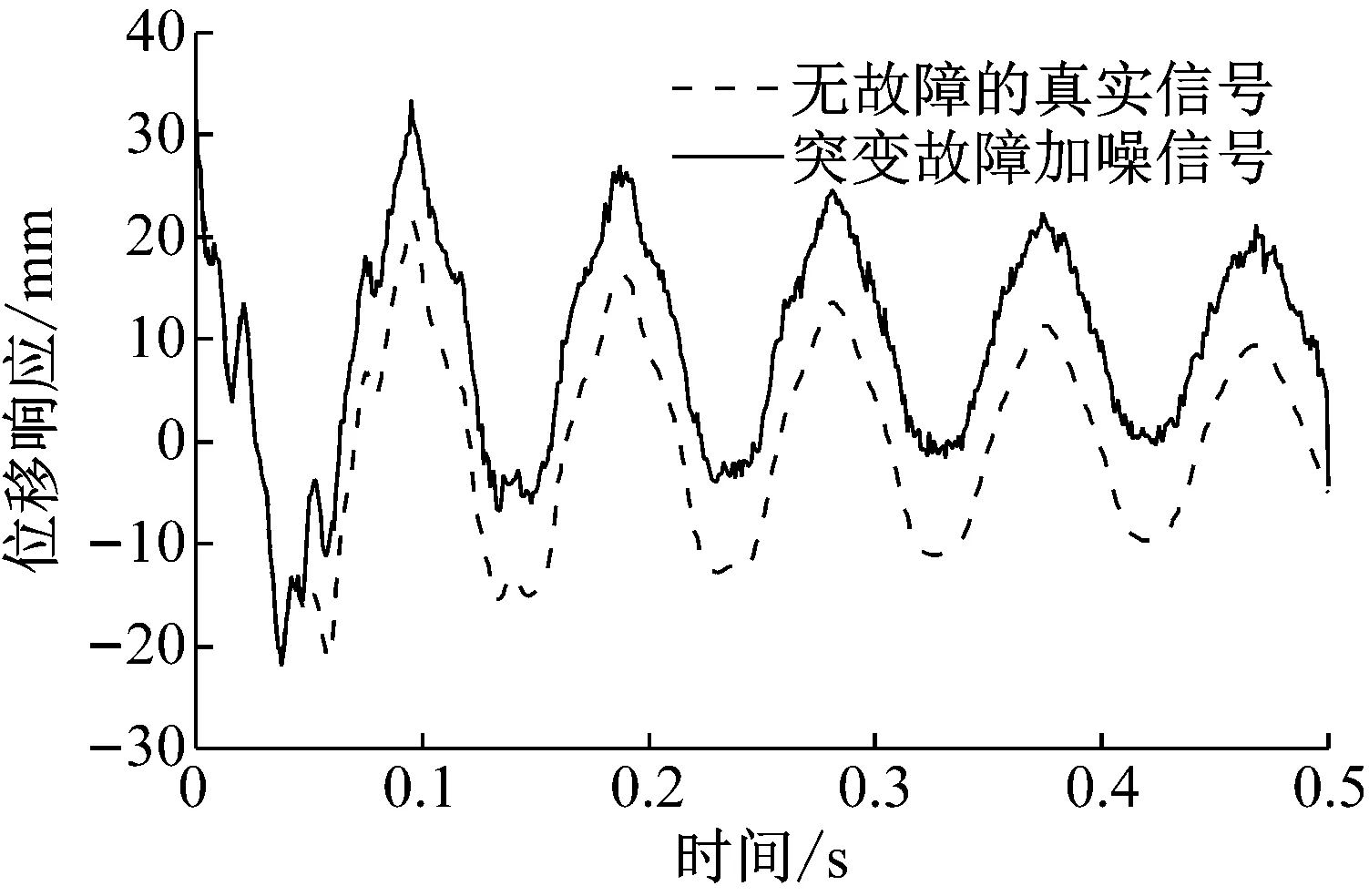
图9 测点5的故障信号(20 dB)

图10 含故障信号的联邦扩展卡尔曼滤波识别结果

在完成故障信号诊断后，即可通过对故障信号的隔离，有效保证损伤识别结果的正确性。图12为剔除故障信号后的联邦扩展卡尔曼滤波损伤识别结果。对比图10和图12可知，联邦扩展卡尔曼滤波方法能结合残差检验法实现对故障传感器信号的检测，通过故障信号隔离以及观测信号的冗余性，保证了结构损伤的正确性与稳定性，有效避免了故障信号导致的损伤误判。

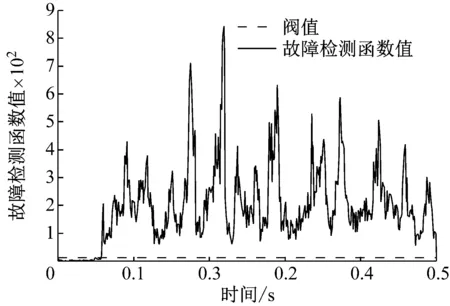
(a) 第一个子滤波器

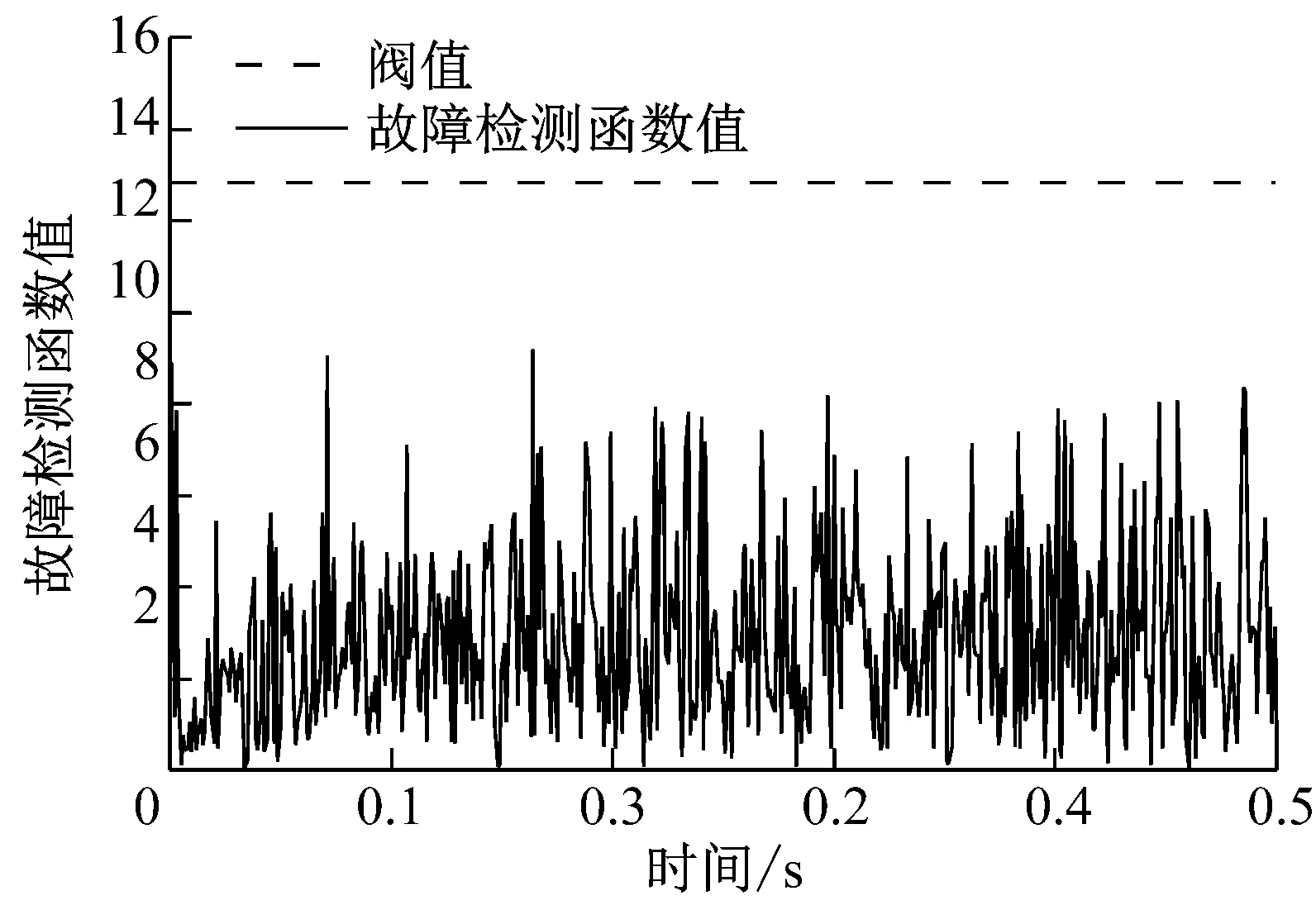
(b) 第二个子滤波器

图12 排除传感器故障后的FEKF损伤识别结果

3 悬臂梁实验分析

实验悬臂梁采用长75 cm，厚0.4 cm，宽4.0 cm的矩形截面钢梁，材料的弹性模量及密度分别为167.64 GPa、7149.2 kg/m3。相应的单元划分、加速度传感器布置和测点分配情况如图13(a)所示。

结构损伤通过在悬臂梁5号单元开孔(Ф=2 cm)模拟。在悬臂梁有限元模型中调整5号损伤单元的弹性模量折减量，使得有限元模型与实际结构固有频率尽量一致，从而可确定实验悬臂梁在5号单元的损伤参数为0.2。

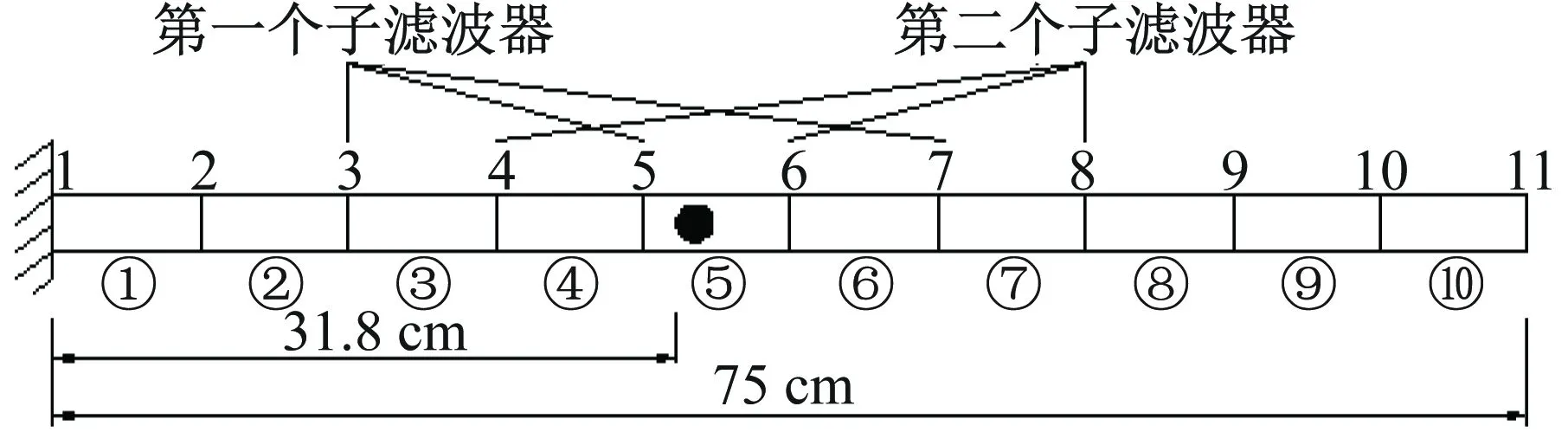
(a) 悬臂梁有限元模型与各子系统测点信号分配

(b) 实验悬臂梁

结构各测点的自由振动信号由力锤激励后测得，采样频率为1 000 Hz。为模拟传感器故障，人为在测点5处振动传感器的测量信号中加入了0.002 m的突变(从0.1 s开始)。

利用本文提出的FEKF算法进行损伤识别。当存在传感器故障时，图14清晰地指示出故障传感器所在的子滤波器，进一步通过传感器交换检测确定故障传感器并进行信号隔离后，本文方法的损伤识别结果如图15所示。为进行对比，图中也列出了无故障传感器时的损伤识别结果。由图示结果可见，无论是否存在故障传感器，本文提出的联邦扩展卡尔曼滤波算法均能通过自主的故障诊断与信号处理，有效识别损伤，具有良好的识别精度与鲁棒性。

(a) 第一个子滤波器

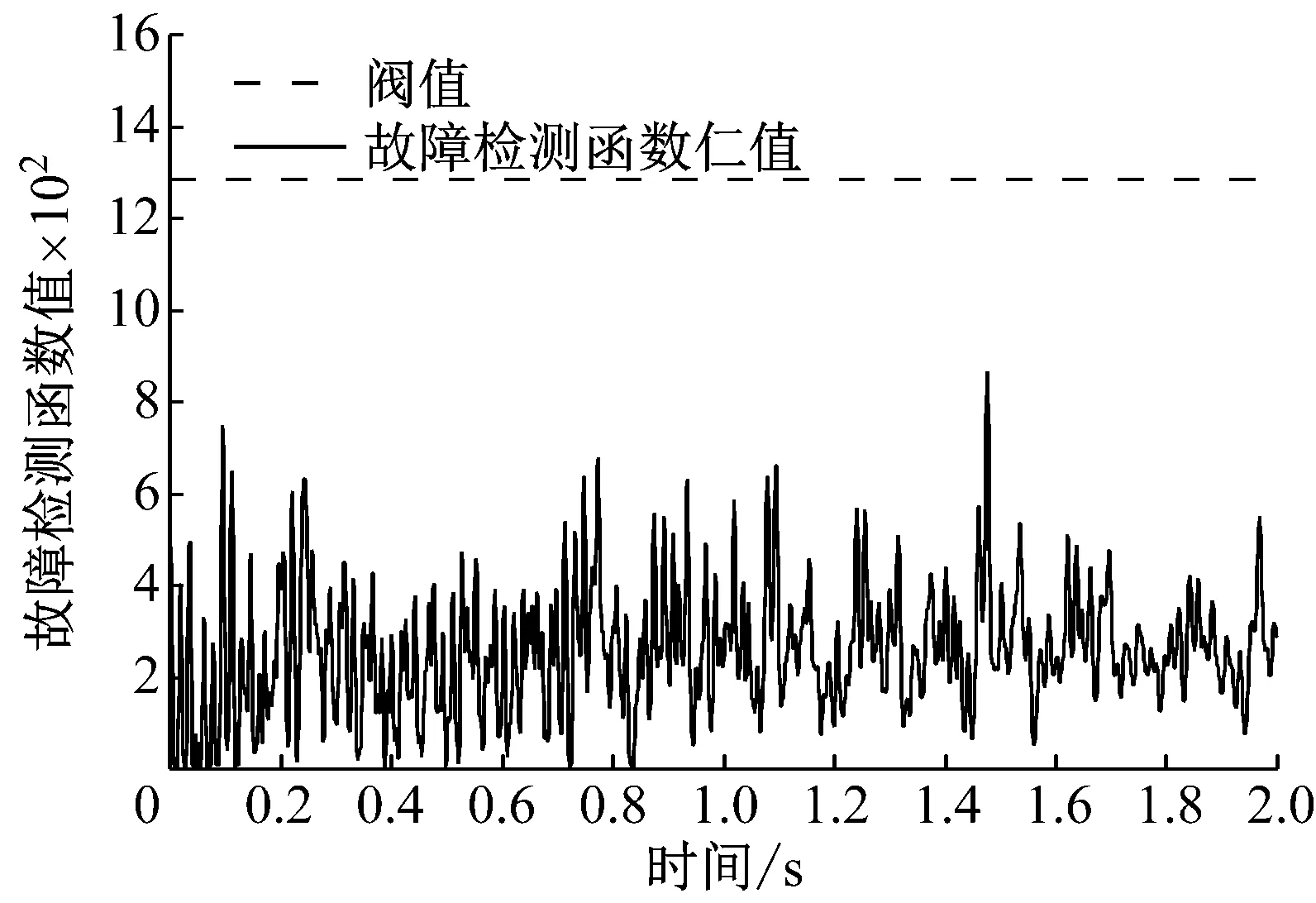
(b) 第二个子滤波器

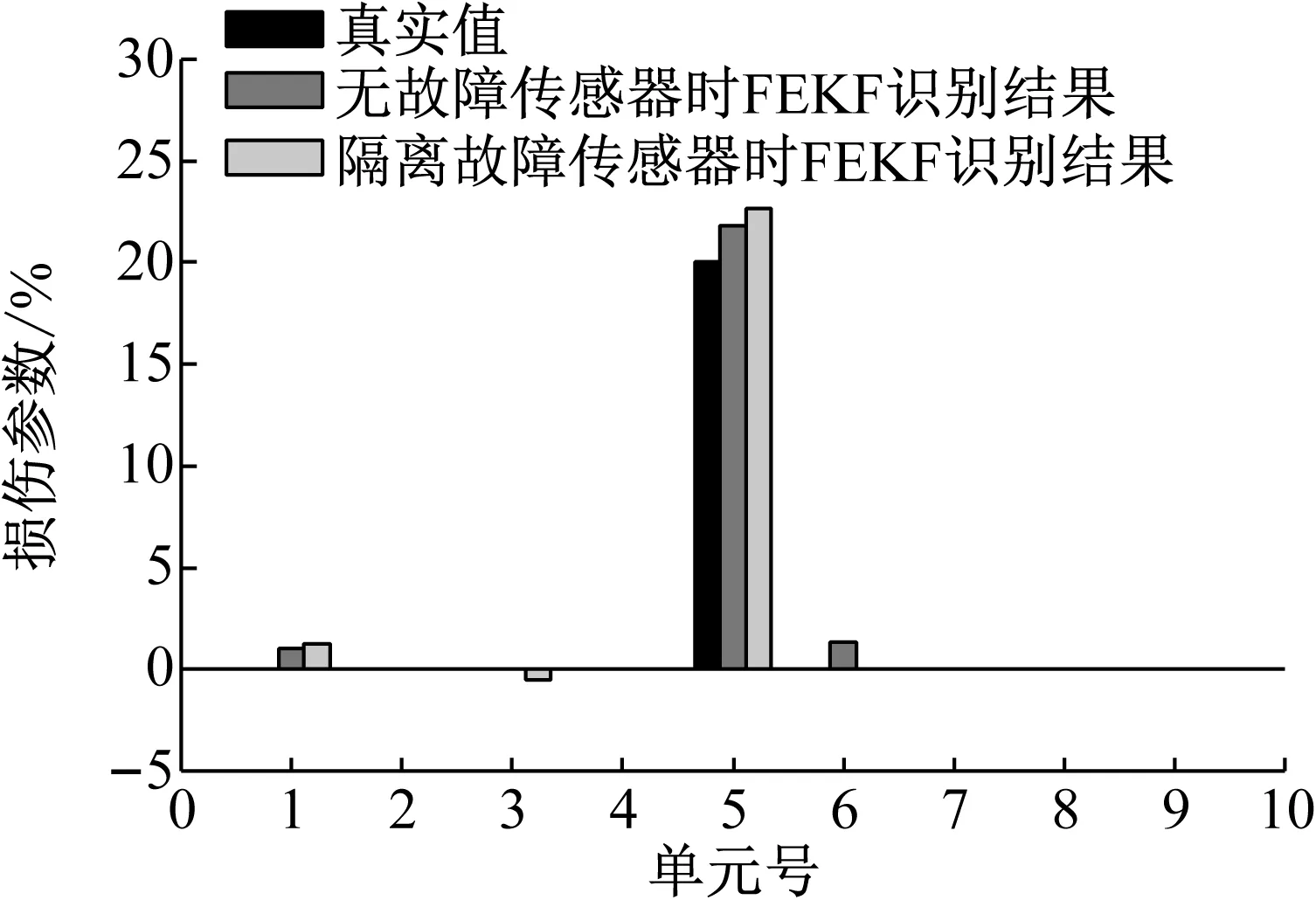
图15 悬臂梁损伤识别结果

4 结 论

本文提出了一种基于联邦扩展卡尔曼滤波的结构损伤识别方法，能利用结构自由振动响应准确识别结构的损伤位置与程度。根据梁式结构的数值模拟结果及实验分析可以得到以下结论：

(1) 在不同的损伤工况下，联邦扩展卡尔曼滤波方法均能准确地识别出结构的损伤位置和损伤程度，且具有很好的鲁棒性。识别精度受噪声影响较小，即使信噪比增大到15 dB，也能保证较高的识别精度。

(2) 当结构损伤和传感器故障同时存在时，联邦扩展卡尔曼滤波算法能结合残差χ2检验法准确识别出故障信号来源，并通过对故障信号的自动剔除，有效保证损伤识别结果的正确性与稳定性。

[1] 雷鹰, 江永强. 输入输出信息有限观测下的结构损伤诊断[J]. 振动、测试与诊断, 2012, 32(5): 736-740.

LEI Ying, JIANG Yongqiang. Structural damage detection technique with limited input and output measurement signals [J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(5): 736-740.

[2] CALABRESE A, SERINO G, STRANO S, et al. An extended Kalman Filter procedure for damage detection of base-isolated structures [P]. 2014 IEEE Workshop on Environmental Energy and Structural Monitoring Systems (EESMS), Naples, Italy. IEEE, USA, 2014.

[3] YANG J N, HUANG H. Sequential non-linear least-square estimation for damage identification of structures with unknown inputs and unknown outputs[J]. International Journal of Non-linear Mechanics, 2007, 42(5): 789-801.

[4] 樊素英, 李忠献. 基于广义卡尔曼滤波的桥梁结构物理参数识别[J]. 计算力学学报, 2007, 24(4): 472-476.

FAN Suying, LI Zhongxian. Identification on physical parameters of bridge structures based on extended Kalman filter[J]. Chinese Journal of Computational Mechanics, 2007, 24(4): 472-476.

[5] 赵博宇, 丁勇, 吴斌. 基于扩展卡尔曼估计算法的地震模拟振动台模型识别 [J]. 振动与冲击, 2014, 33(12): 145-150.

ZHAO Boyu，DING Yong，WU Bin. Identification of shaking table model for seismic simulation based on an extended Kalman estimator[J]. Journal of Vibration and Shock, 2014, 33(12): 145-150.

[6] 谢献忠, 易伟建. 结构物理参数时域识别的子结构方法研究[J]. 工程力学, 2005, 22(5): 94-98.

XIE Xianzhong, YI Weijian. A substructure method for parameter estimation in time domain[J]. Engineering Mechanics, 2005, 22(5): 94-98.

[7] 穆腾飞, 周丽. 输入未知条件下基于自适应广义卡尔曼滤波的结构损伤识别[J]. 振动工程学报, 2014, 27(6): 827-834.

MU Tengfei, ZHOU Li. Structural damage identification using adaptive extended Kalman filter with unknown inputs[J]. Journal of Vibration Engineering, 2014, 27(6): 827-834.

[8] 周东华, 胡艳艳. 动态系统的故障诊断技术[J]. 自动化学报, 2009, 35(6):748-758.

ZHOU Donghua, HU Yanyan. Fault diagnosis techniques for dynamic systems[J]. Acta Automatica Sinica, 2009, 35(6):748-758.

[9] CARLSON N A, BERARDUCCI M P. Federated kalman filter simulation result[J]. Journal of the Institute of Navigation, 1994, 41(3): 297-321.

[10] 卞鸿巍, 李安, 覃方君. 现代信息融合技术在组合导航中的应用[M]. 北京: 国防工业出版社, 2010.

[11] 戴霖. 基于扩展卡尔曼滤波的结构损伤识别方法[D]. 南昌： 南昌大学, 2014.

[12] WEBER B, PAULTRE P, PROULX J. Consistent regularization of nonlinear model updating for damage identification[J]. Mechanical Systems and Signal Processing, 2009, 23(6): 1965-1985.

Structuraldamageidentificationbasedonthefederalextendedkalmanfilter

ZHANGChun,WANGLudan,SONGGuquan,XUChanghong,LIAOQun

(School of Civil Engineering and Architecture, Nanchang University, Nanchang 330031, China)

The coexistence of structure damages and sensor faults will deteriorate identified results evidently, so an algorithm for the identification of structure damages based on the Federated Extended Kalman Filter method (FEKF) was proposed by using free vibration signals. The presented method can identify the location and extent of damages accurately, and shows good robustness when the sensors work normally. Combined with the residual chi-square test, the FEKF also can eliminate the effects of fault sensors by the automatic detection and removal of the fault sensor signals. Numerical simulations and experiments show that the FEKF can ensure the accuracy and stability of the damage identification results and detect fault signals effectively.

federal extended Kalman filter; damage identification; sensor fault; residual chi-square test; decentralized filtering

TU311

A

10.13465/j.cnki.jvs.2017.21.027

国家自然科学基金(51268045;51469016);教育部高等学校博士点基金(20123601120011);水沙科学与水利水电工程国家重点实验室开放研究基金(sklhse-2014-C-03);广东省水利科技创新基金(2014-08)

2015-12-23 修改稿收到日期：2016-07-09

张 纯 男，博士，教 授，1976年10月

宋固全 男，博士，教 授，1964年2月