水下加筋圆柱壳声辐射特性分析的改进精细传递矩阵法

庞福振， 吴 闯， 王献忠， 姚熊亮

(1. 哈尔滨工程大学 船舶工程学院，哈尔滨 150001； 2. 海军装备研究院，北京 100161；3. 上海交通大学 机械系统与振动国家重点实验室，上海 200240)

水下加筋圆柱壳声辐射特性分析的改进精细传递矩阵法

庞福振1，2， 吴 闯3， 王献忠1， 姚熊亮1

(1. 哈尔滨工程大学 船舶工程学院，哈尔滨 150001； 2. 海军装备研究院，北京 100161；3. 上海交通大学 机械系统与振动国家重点实验室，上海 200240)

基于Flügge壳体振动理论，将改进精细传递矩阵法应用于水下加筋柱壳声辐射问题的求解；通过应用加法定理和增量存储，改进非齐次项求解方法，构造了加筋圆柱壳的辐射噪声改进精细传递矩阵法。分析了边界条件、结构损耗因子、流体介质以及壳体厚度对加筋圆柱结构声辐射的影响。研究表明，当边界条件从自由、简支到刚固，结构对外辐射声压逐渐降低；随着结构损耗因子的增大，结构对外辐射声压大体上逐渐降低。

非齐次项； 精细积分传递矩阵； 加筋圆柱壳； 振动； 声辐射

在实际工程中，特别是在现代国防军事领域，加筋圆柱壳是众多武器装备的基本简化模型，如：鱼雷、导弹、潜艇等。因此对于加筋圆柱壳的声振耦合机理分析，一直以来是国内外学者的研究热点。在数值方面，FEM、BEM方法、SEA方法等方法得到了广泛应用[1]。数值方法理论上来说能够处理任意复杂的结构，但其求解精度受限于计算频段，建模周期长，而且数值方法难以进行机理分析，这些均制约了有限元技术的发展。而传统的解析方法只能给出简单结构的解析解。因此半解析半数值法逐渐成为进行加筋圆柱壳声辐射分析的一种有效方法。其中，传递矩阵法由于其对求解链状结构动力问题的巨大优势，而受到国内外学者青睐。

Tottenham等[2]首先给出了一种求解圆柱壳结构自由振动的传递函数分析方法。后来Irie等[3]进行进一步推广应用，形成了较为完善的传递矩阵方法，并将其成功应用到轴向具有离散弹簧支承性壳体结构的自由振动问题上，这些研究均是围绕结构的自由振动特性进行展开研究的，并没有涉及到壳体结构振动响应和水下声辐射的问题。蔡显新[4]以旋转壳结构为计算模型，借鉴了Irie等的思想，将旋转壳的状态向量沿周向以级数形式展开，推导了旋转壳的一阶振动微分方程，给出了一种求解旋转壳自由振动的半解析解，然而该方法精度有限，要求离散的分段较细。曹雷等运用Riccati传递矩阵法分析了水下有限长环肋圆柱壳的声辐射性能，但是在计算一阶非齐次矩阵微分方程的非齐次项时，采用了分段插值理论对非齐次项进行多项式逼近，难免会出现数值不准确，精度损失的问题。

为此，针对以上的不足，提出一种精细积分传递矩阵法。该方法主要用来解决结构振动响应和水下声辐射的问题，对于文献[5]，在计算一阶非齐次矩阵微分方程的非齐次项时，采用分段插值理论对非齐次项多项式逼近的方法所带来数值不准确，精度损失的问题，本文采用了一种精度更高的处理方法，即谭述君等[6]提出的非齐次项精细积分法。该方法将柱壳微段划分为精细积分步，基于积分步内的Taylor级数展开和加法定理，循环处理得到柱壳微段内非齐次项的高精度结果，数值计算时精度更高更准确。

1 理论推导

1.1 圆柱壳的场传递矩阵

本文研究的模型为浸没在无限流场介质中的有限长加筋圆柱壳，其中假设圆柱壳两端为无限大刚性障板，模型如图1所示。

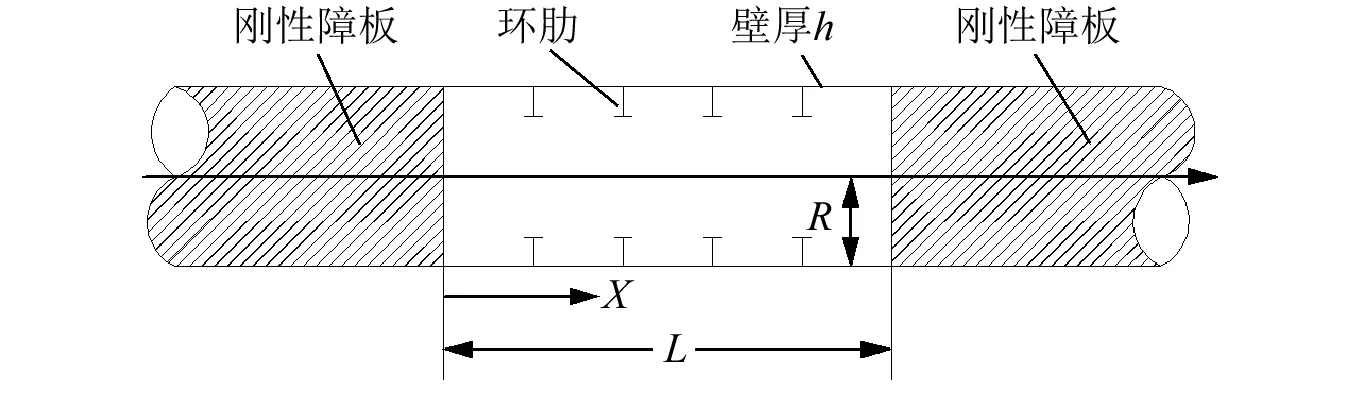
图1 加筋圆柱壳模型示意图Fig.1 Model of stiffened cylindrical shell

壳体变形通常采用基于直线假设的薄壳理论进行描述，为了得到精准的数值，本章采用相对比较精确的Flügge壳体理论[7]，柱壳的微元进行受力分析，得到力的平衡方程。由于本文是基于动力学理论建立的方程，很多项中都包含时间项，为了方便书写和推导，在下文的书写中将略去动响应的时间项e-iωt， 圆柱壳坐标系(γ,φ,x)以及位移正方向，如图2所示。

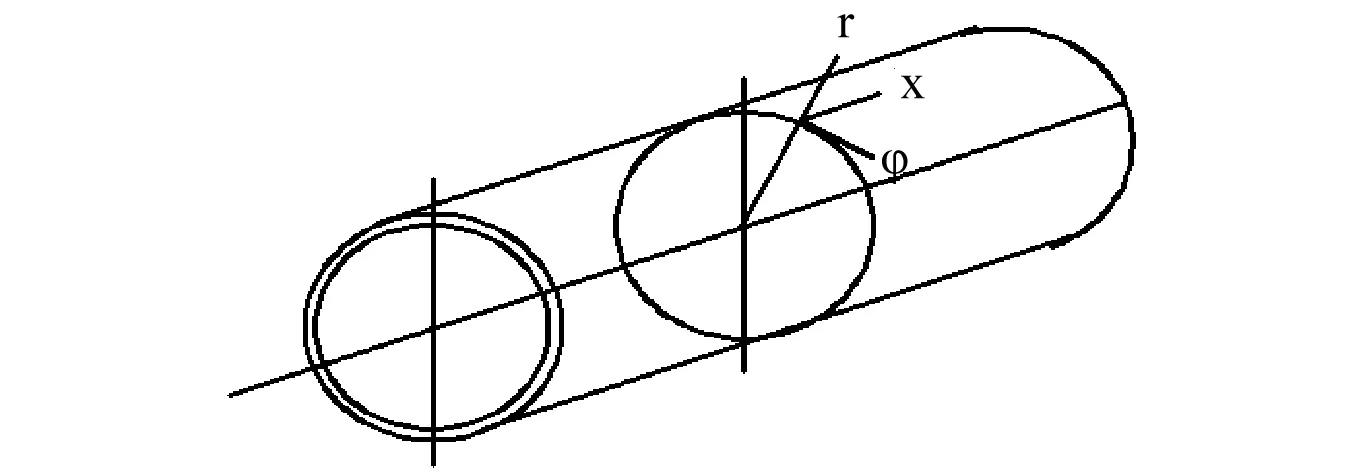
图2 圆柱壳坐标系Fig.2 Cylindrical shell coordinates system

根据Flügge壳体理论，壳体力平衡方程为

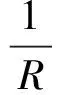
(1)

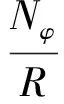
(2)

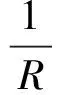
(3)

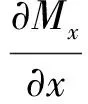
(4)

通过消除8个未知量，保留8个未知量，将各量无量纲化并沿周向展成三角函数形式，经过化简得到一阶矩阵微分方程

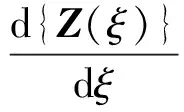
(5)

1.2 环肋的点传递矩阵

由于环肋的作用，圆柱壳的状态向量在环肋处发生改变，利用环肋与壳体连接处的连续条件和环肋的运动控制方程(面内的拉伸和弯曲振动，面外的弯曲和扭转振动)很容易得到环肋的点传递矩阵Rk。圆柱壳上某一环肋位置处ξk处，由于环肋的存在，环肋左端、右端的壳体中两个面内力和两个面外力发生变化，状态向量满足式(6)

(6)

式中，Rk为8×8的点传递矩阵，矩阵中各非零元素为Rii=1,i=1,2,…,8。

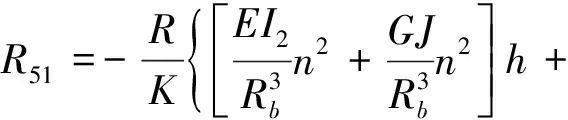
(7)

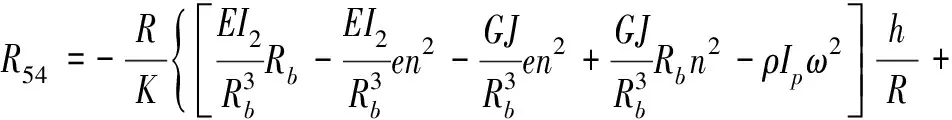
(8)

(9)

(10)

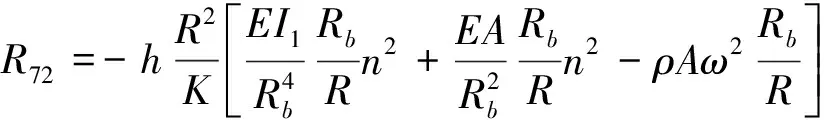
(11)

(12)

(13)

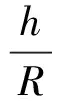
(14)

式中：Rb、I1、I2、IP、J分别为环肋的中和轴半径、对纵向对称轴的惯性矩、对径向对称轴的惯性矩、极惯性矩以及扭转常数；A,ρ,G分别为环肋截面积、密度、剪切模量；E为复合弹性模量；E=E0(1+iη)，E0为弹性模量；η为损耗因子。Rb=R+e；e为偏心距，内肋取负号，外肋取正号。

1.3 非齐次项动力响应的处理问题

对于线性非齐次微分方程式(5)，其一般解为

(15)

式中：r(τ)={F(ξ)}-{p(ξ)}右端第二项为非齐次项引起的状态响应；对上式各项的求解是解决声辐射问题的第一步，也是非常重要的一步。eUΔξ的求解可参考文献[8]的指数矩阵精细积分法。因此，只要解出非齐次项就可以得到状态向量Z(ξ)， 采用精细积方法处理非齐次项。

外流场用Helmholtz方程表示为

(16)

声压满足无穷远处边界条件和端面边界条件为

(17)

(18)

Helmholtz方程可采用分离变量的办法，考虑式(17)、式(18)等边界条件，则周围流体域的辐射声压可表示为

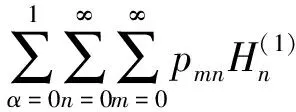
(19)

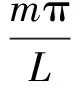
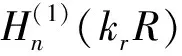
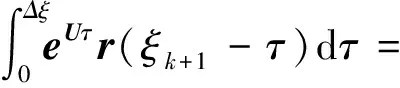
(20)

式中，e为已知项。

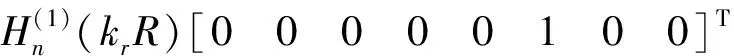
令

α=ikml

(21)

pp=ecos(kmlξk+1)

(22)

qq=esin(kmlξk+1)

(23)

则式(20)可改写为

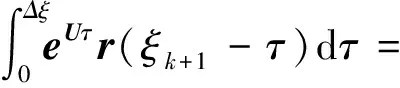
(24)

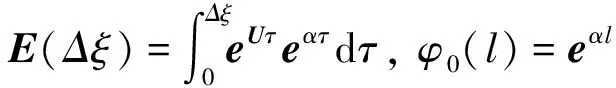
由加法定理可得

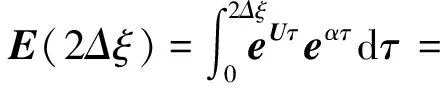
(25)

同理可得

Φ0(2Δξ)=(Φ0(Δξ))2

(26)

φ0(2Δξ)=(φ0(Δξ))2

(27)

当基本区段Δξ划分为精细区段τ(τ=Δξ/2M)时，M建议取20。E(τ)、Φ0(τ)、φ0(τ)可采用Taylor级数展开有限项进行近似

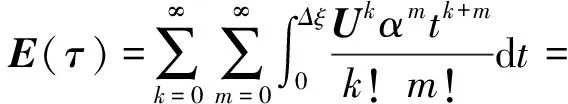
(28)

(29)

(30)

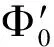
(31)

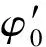
(32)

根据式(25)可得

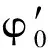
(33)

令E1为E(τ)的实部

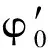
(34)

令E2为E(τ)的虚部

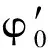
(35)

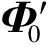
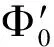
(36)

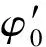
(37)

(38)

(39)

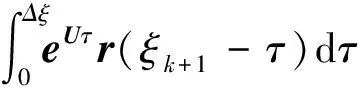
(40)

至此，已利用精细区段的加法定理求出非齐次项的精细结果。同时可将声压作用下的式(15)写成矩阵的形式

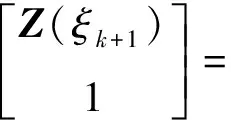
(41)

集中力对圆柱壳的作用与环肋类似，仅仅改变了集中力处得状态向量，故集中力左右两端满足式(42)

(42)

式中：Fk=RK-1[0 0 0 0 0fn0 0]T；IFk为集中力的点传递矩阵。

1.4 加筋圆柱壳声辐射的求解

1.4.1 集中力作用下的状态向量

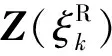
(43)

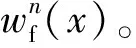
1.4.2 声压作用下的状态向量

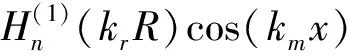
(44)

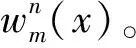
1.4.3 声辐射的求解

根据线性叠加原理，对应于任意阶周向波数n下的径向位移满足

(45)

但是pmn是未知的，故必先求解pmn才能得到wn(x)。

根据连续性条件，在流体与结构的接触面上，流体径向速度必须等于结构的径向速度

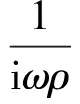
(46)

由于结构界面处上任意一点均满足连续条件，因而可在结构长度方向进行取M个点，其中M既要大于波数m，又要满足M=2πλ-1。取M个点代入式(46)中，并将式(19)、式(45)代入式(46)中，则可转化为求解各波数对应的声压系数的方程

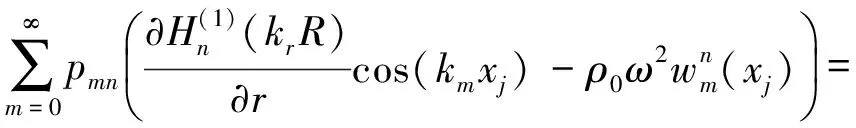
(47)

可通过Moore-Penrose广义求逆法求解。具体过程为pmn

令

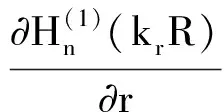
(48)

(49)

显然上式中只有一个未知的列向量{pm1}n，所以可以求解。

[U]n{p}n={Q}n

(50)

将[U]进行奇异值分解，可得

[U]=[A][D][V]T

(51)

对矩阵[U]进行Moore-Penrose求逆，可得

[U]-1=[V][D]-1[A]T

(52)

将其代入式(24)，可得

(53)

将求得的系数矩阵{p}代入式(19)，可得到流场中的辐射声压。由水下辐射声压可求解对应的辐射声压级：Lp=20 lg(p/p0)，参考基准声压值为1 μPa。圆柱壳上任意一点的径向位移为

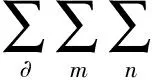
(50)

结构表面径向均方振速为

(51)

速度级为

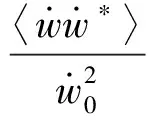
速度级的基准为

2 PITMM的验证与数值计算

2.1 验证模型简介

采用文献[9-10]和文献[5]中的数据对本文方法的准确性进行验证。对比结果见表1、表2。

文献[9]中参数为:材料E0=2.06×1011Pa; 泊松比μ=0.3; 密度ρ=7 800 kg/m3; 损耗因子取η=0.01； 密度ρ0=1 000 kg/m3; 声波传播速度取c0=1 500 m/s； 柱壳几何参数长L=0.6 m; 半径R=0.2 m; 厚度h=0.003 m; 柱壳的内肋为0.002 m×0.030 m; 环肋数量9根。径向激励力作用在壳体(L/2,0,R)处，幅值为1 N。 测量点为(L/2,θ,2 m)。

文献[10]中参数为:材料、流体介质参数同文献[9]。柱壳几何参数长L=0.6 m; 半径R=0.175 m; 厚度h=0.002 m; 柱壳的外肋0.002 m×0.025 m; 环肋数量5根。 径向激励力作用在壳体(L/2,0,R)处， 幅值为1 N。测量点(L/2,θ,1.175 m)， 如图3所示。

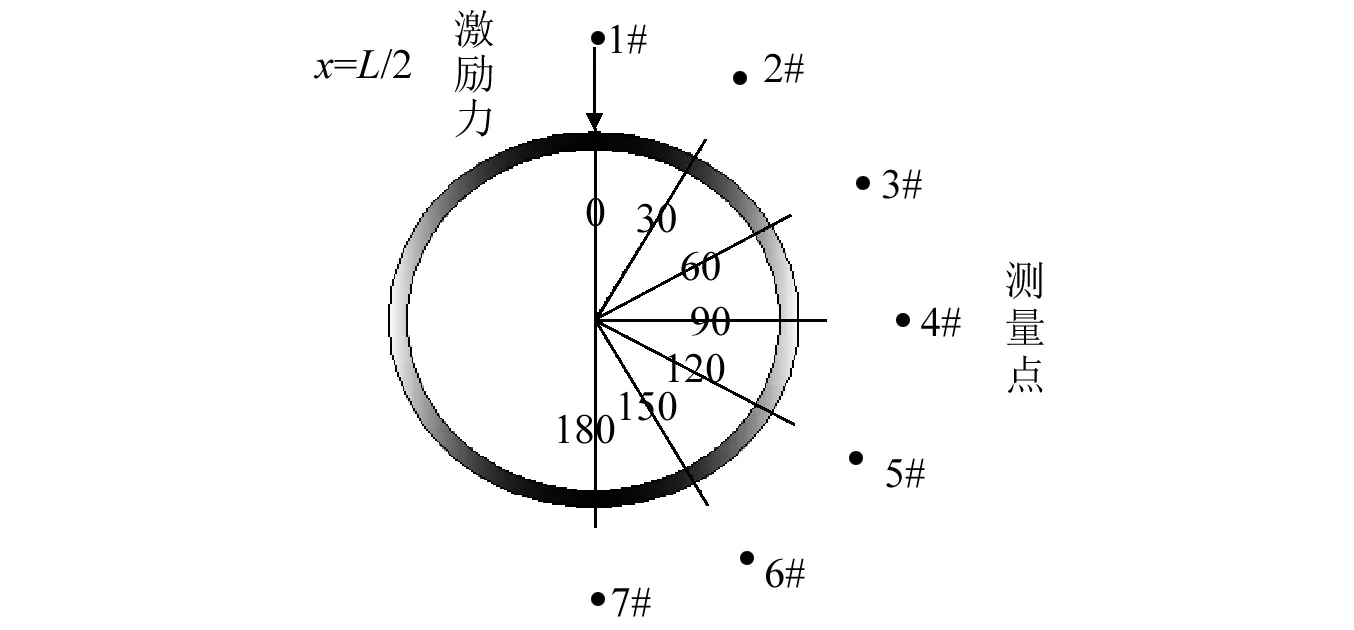
图3 验证模型示意图Fig.3 Model schematic diagram

2.2 计算结果的对比

(1) 算例1与公开文献数据对比。

(2) 算例2与公开文献数据对比。

文献[9]采用能量法,用Hamilton原理和Green函数方法研究环肋柱壳的声辐射特性；文献[10]基于Flügge壳体理论，仅考虑径向激振力，计及壳体受环肋的反力和反力矩作用，分析加筋柱壳的声辐射特性。通过表1、表2中试验值与计算值对比分析可知，本文方法较文献[5]、文献[9]方法精度要高，与文献[10]方法精度相当，除精度高外，本文方法最大特点是易于编程，计算效率高。

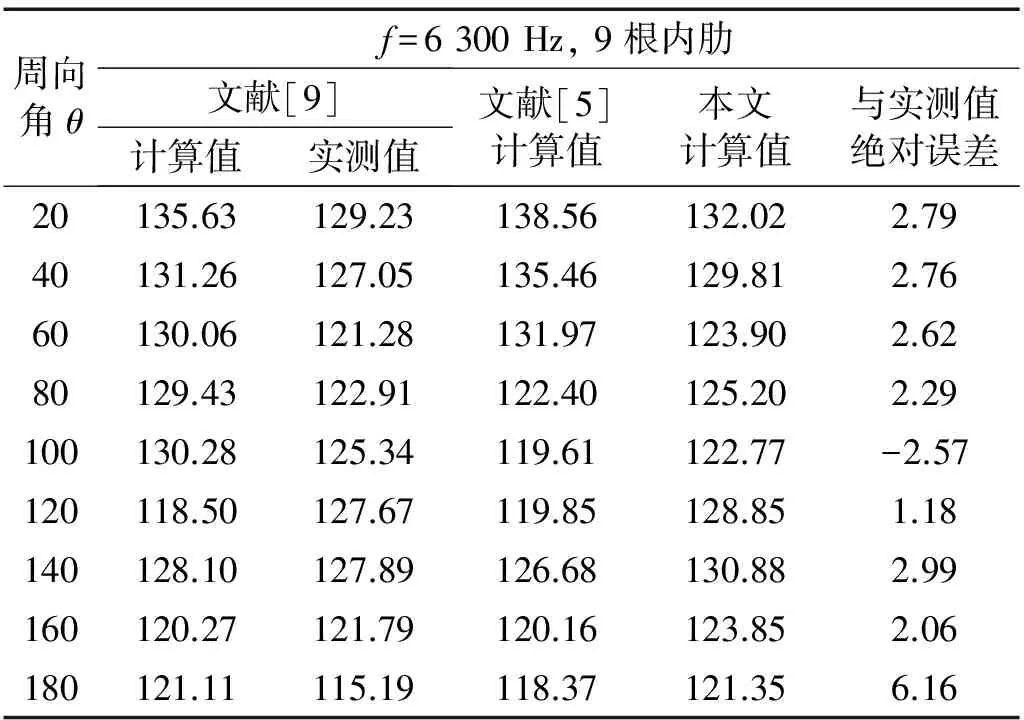
表1 简支加筋柱辐射声压级对比

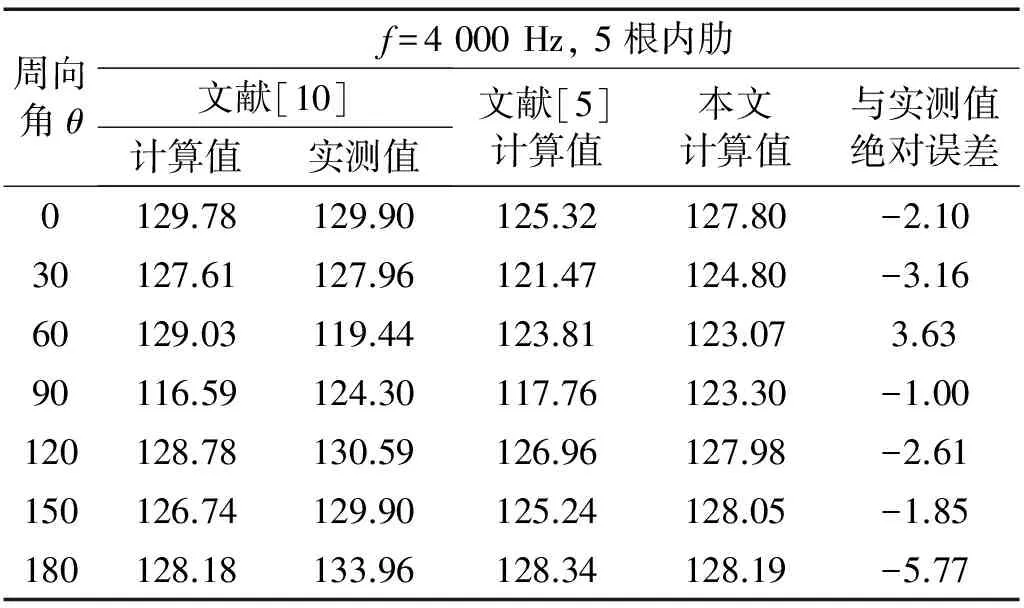
表2 简支加筋柱壳辐射声压级对比

3 加筋柱壳结构振动噪声特性研究

采用文献[10]的模型参数，基于非齐次项精细积分传递矩阵法分析加筋柱壳的一些参数对声辐射的影响。除“3.1”节算例外，其余算例中模型边界条件均为两端简支，模型自振频率计算值如表3所示。表3中，m为纵向半波数，n为周向波数。

3.1 边界条件对加筋柱壳辐射噪声的影响

加筋圆柱壳模型两端边界分别是两端自由(F-F)、两端简支(S-S)、两端刚固(C-C)。声压测量点为(L/2,θ,1.175 m)，即柱壳长度中点处周向一系列点。模型计算频率点为f=4 000 Hz，对比结果见图4。

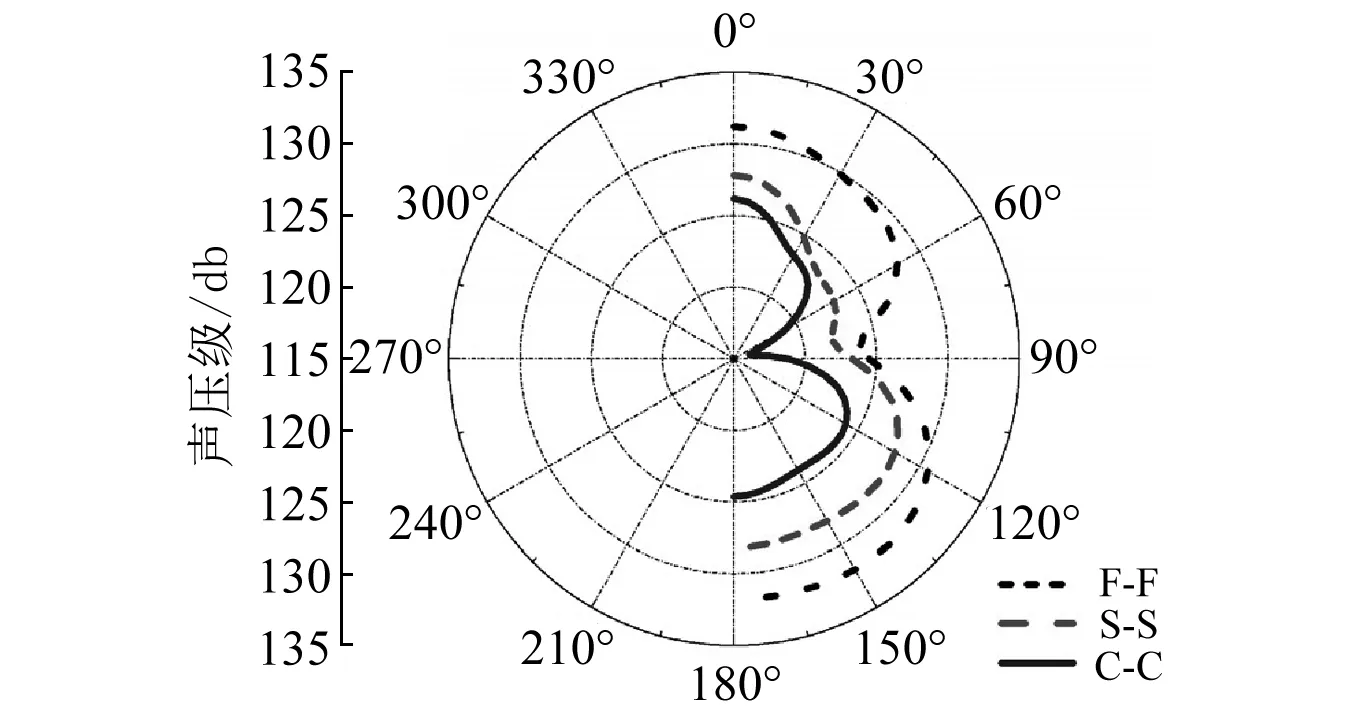
图4 各测点不同边界辐射声压级图线Fig.4 Circumferential cylindrical shell SPL

图4比较了两端不同边界条件对水下加筋柱壳辐射声压级的影响。从图4可知，两端边界条件从自由、简支、到刚固，随着固定的加强，结构对外辐射声压逐渐降低，这是因为两端固定越强结构产生振动越困难，辐射声压也就越小。

3.2 结构损耗因子对加筋柱壳辐射声压级的影响

加筋圆柱壳模型的结构损耗因子分别为η=0.01；η=0.05；η=0.1。声压测量点为(L/2,θ,1.175 m)，即柱壳长度中点处周向一系列点。模型计算频率点为f=4 000 Hz。对比结果见图5。

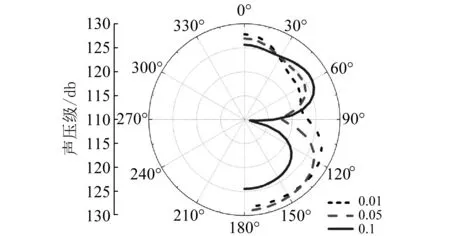
图5 各测点不同阻尼辐射声压级图线Fig.5 Circumferential cylindrical shell SPL

图5比较了不同结构损耗因子对水下加筋柱壳辐射声压级的影响。由图5可知，当损耗因子较小时(η=0.01和η=0.05)，其对加筋柱壳水下辐射声压影响不明显，而当损耗因子较大时(η=0.1)，其对加筋柱壳水下辐射声压影响显著。从声压分布来看，在靠近激励力处(θ=0°)，损耗因子对结构辐射声压影响小；在远离激励力处(θ=180°)，损耗因子对结构辐射声压影响大。

3.3 流体介质对加筋柱壳辐射声压级的影响

水的质量密度为1 000 kg/m3；声在水中的传播速度1 500 m/s；空气的质量密度为1.293 kg/m3；声在空气中传播速度为340 m/s。声压测量点为(L/2,θ,1.175 m)，即柱壳长度中点处周向一系列点。模型计算频率点为f=4 000 Hz。对比结果见图6。

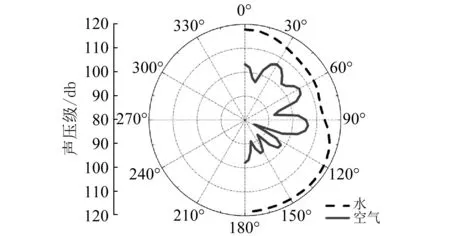
图6 各测点不同介质辐射声压级图线Fig.6 Circumferential cylindrical shell SPL

图6比较了不同流体介质对加筋柱壳辐射声压级的影响，由图6可知，结构在流体介质阻抗大的水中比在体介质阻抗小的空气中对外辐射声压明显要大，因为水的阻抗相对空气要大，声波造成水介质的压强变化量大于空气，故出现此现象。

3.4壳体厚度对加筋柱壳径向均方振速级和辐射声压级的影响

加筋圆柱壳模型的壳体厚度分别为h=0.002 m；h=0.01 m；h=0.02 m。结构表面径向均方振速测量点(L/2,0,R)，流场中声压测量点(L/2,0,1.175 m)，模型计算频域0～1 000 Hz。对比结果见图7、图8。

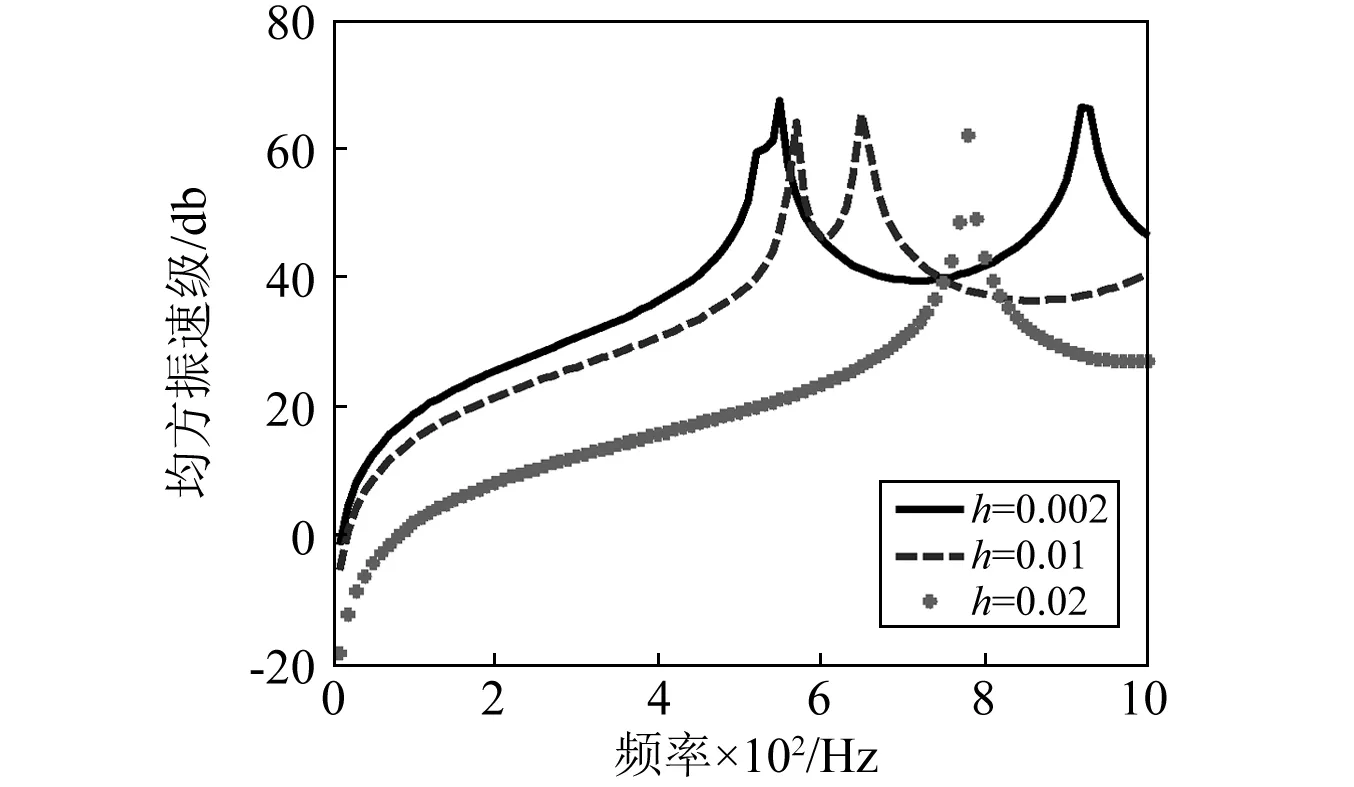
图7 不同壳体厚度加筋柱壳径向均方振速级的对比Fig.7 Lv(db) comparison of stiffened cylindrical shell with different thickness

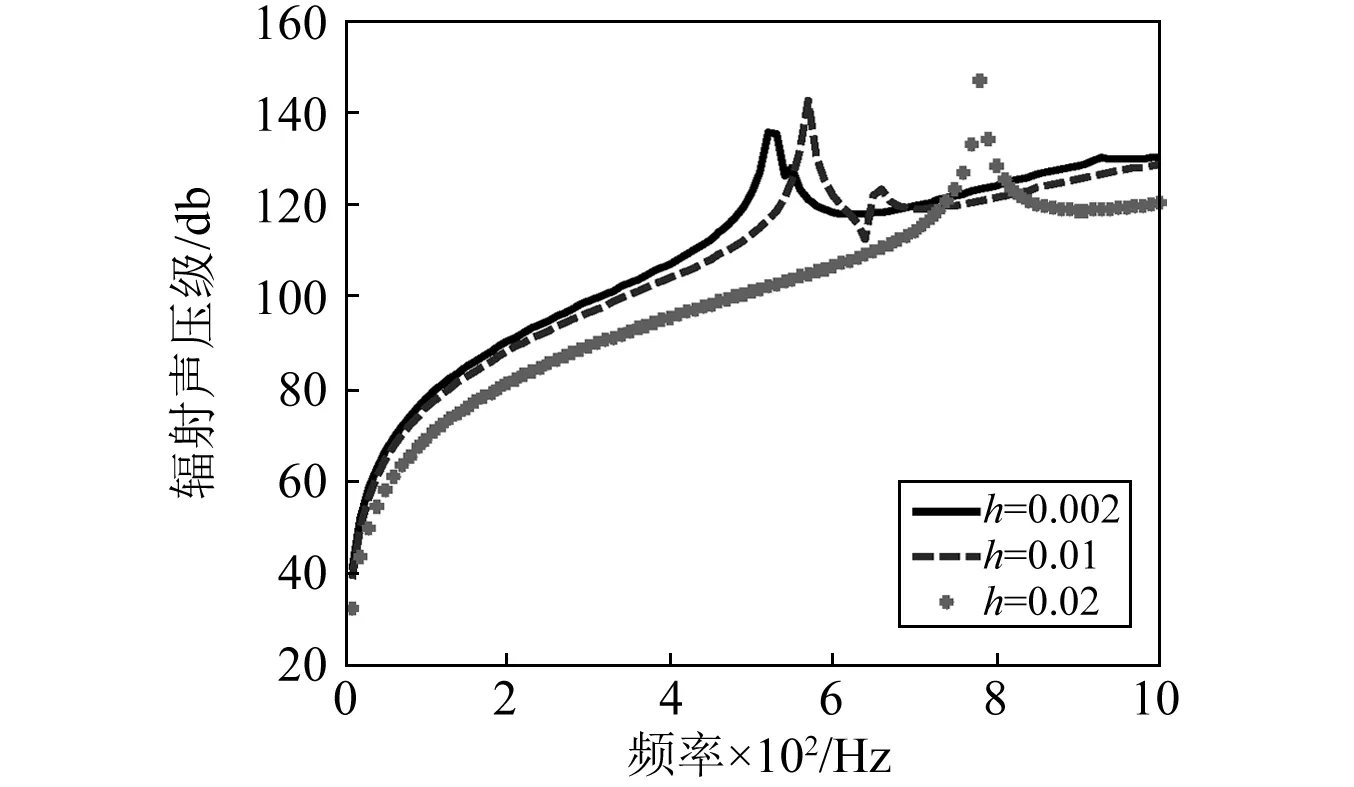
图8 不同壳体厚度加筋柱壳辐射声压级的对比Fig.8 SPL(db) comparison of stiffened cylindrical shell with different thickness

图7、图8比较了不同壳体厚度对水下加筋柱壳径向均方振速级和辐射声压级的影响。从图7可知，随着壳体厚度的增加径向均方振速级的峰值点向后推移，峰值大小基本无变化；在非峰点区，随着壳体厚度的增加，加筋柱壳径向均方振速逐渐减小。从图8可知，随着壳体厚度的增加辐射声压级的峰值点也向后推移；在非峰点区，基本满足随着壳体厚度的增加，加筋柱壳辐射声压级逐渐减小的规律。对于峰值点向后推移，是因为随着壳体厚度的增加，结构刚度增加，其自振频率也随之增加。

4 结 论

针对传统传递矩阵法以及精细传递矩阵法在处理非齐次项的不足，通过将非齐次方程Duhamel项精细积分法引入精细传递矩阵法，构造了求解水下加筋柱壳声辐射问题的改进精细传递矩阵法，该方法采用积分步内Taylor级数展开和加法定理，具有计算精度高、易于编程的优点。通过将本文方法计算结果与公开文献、有限元等计算结果进行比较，以验证本文方法的有效性。在此基础上，分析了加筋柱壳边界条件、结构损耗因子、流体介质及壳体厚度等参数的改变对其水下声辐射特性的影响规律。其中，流体介质的改变对加筋柱壳水下声辐射影响最大，结构在阻抗大的介质中声辐射明显大于阻抗小的介质；边界固定越强，加筋柱壳向外辐射能力越低，辐射声压越小；损耗因子越大，吸收结构振动的能量越多，造成加筋柱壳向外辐射声压越小；壳体厚度对柱壳辐射声压的影响，基本满足随着壳体厚度增加辐射声压逐渐减小的规律。

[ 1 ] 瞿叶高, 华宏星, 孟光，等.基于区域分解的圆锥壳-圆柱壳-圆锥壳组合结构自由振动[J].振动与冲击，2012, 31(22): 1-7.

QU Yegao, HUA Hongxing, MENG Guang, et al. A domain decomposition method for free vibration analysis of joined conical-cylindrical-conical shell [J]. Journal of Vibration and Shock, 2012, 31(22): 1-7.

[ 2 ] TOTTENHAM H, SHIMIZU K. Analysis of the free vibration of cantilever cylindrical thin elastic shells by the matrix progression method [J]. International Journal of Mechanical Sciences, 1972, 14(5): 293-310.

[ 3 ] IRIE T, YAMADA G, MURAMOTO Y. Free vibration of joined conical-cylindrical shells [J]. Journal of Sound and Vibration, 1994, 95(1): 31-39.

[ 4 ] 蔡显新.计算旋转薄壳自由振动的传递矩阵法[J].航空学报,1992,13(1): 64-70.

CAI Xianxin. A TMM the free vibration of shellls of revolution [J]. Acta Aeronautica et Estronautica Sinica, 1992, 13(1): 64-70.

[ 5 ] 曹雷,马运义，黄玉盈，等.基于raccati传递矩阵法分析水下有限长环肋圆柱壳的声辐射性能[J].振动与冲击,2009, 28(9): 149-154.

CAO Lei, MA Yunyi, HUANG Yuying, et al. Analysis of acoustic radiation of ring-stiffened cylindrical shell with finite length in underwater based on riccati transfer matrix method [J]. Journal of Vibration and Shock, 2009, 28(9): 149-154.

[ 6 ] 谭述君, 钟万勰.非齐次动力方程duhamel项的精细积分[J].力学学报,2007, 39(3): 374-381.

TAN Shujun, ZHONG Wanxie. Precise integration method for duhamel terms arising from non-homogenous dynamic systems [J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(3): 374-381.

[ 7 ] 陈美霞, 骆东平, 杨叔子.壳间连接形式对双层壳声辐射性能的影响[J].振动与冲击,2005, 24(5): 77-80.

CHEN Meixia, LUO Dongping, YANG Shuzi. Effect of connection type between inner and outer shells on characteristics of sound radiation from finite double cylindrical shell [J]. Journal of Vibration and Shock, 2005, 24(5): 77-80.

[ 8 ] 钟万勰.结构动力方程的精细时程积分法[J].大连理工大学学报,1994, 34(2): 131-136.

ZHONG Wanxie. On precise time-integration method for structural dynamics [J]. Journal of Dalian University of Technology, 1994, 34(2): 131-136.

[ 9 ] 陈美霞, 骆东平,曹钢，等.环肋柱壳振动和声辐射试验分析[J].华中科技大学(自然科学版),2003,31(4): 102-104.

CHEN Meixia, LUO Dongping, CAO Gang, et al. Analysis of vibration and sound radiation from ring-stiffened cylindrical shell [J]. Journal of Huazhong University (Science and Technology), 2003, 31(4): 102-104.

[10] 谢官模, 骆东平.环肋柱壳在流场中声辐射性能分析[J].中国造船,1995,131(4): 37-45.

XIE Guanmo, LUO Dongping. Acoustic radiation analysis of ring-stiffened cylindrical shells in fluids[J]. Ship Building of China, 1995, 131(4): 37-45.

附录A

Animprovedprecisetransfermatrixmethodfortheanalysisofacousticradiationofring-stiffenedcylindricalshells

PANG Fuzhen1,2, WU Chuang3, WANG Xianzhong1, YAO Xiongliang1

(1. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China; 2. Naval Academy of Armament, Beijing 100161, China; 3. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 200240, China)

Based on the Flügge shell theory, an improved precise transfer matrix method (IPTMM) was applied to the solution of acoustic radiation for stiffened cylindrical shells. According to the techniques of addition theorem and increment storage, calculation of inhomogeneous was improved. Then, the improved precise transfer matrix method was obtained. The effects of different end boundary condition, structural damping, fluid medium and shell thickness were presented. The results show that when the boundary conditions from freedom supported and simply supported change to rigidly fixed, external radiation acoustic pressure of structure gradually reduces. With the increasing of structural damping, external radiation acoustic pressure of structure gradually reduces.

non-homogeneous item; precise integration transfer matrix; ring-stiffened cylindrical shell; vibration; acoustic radiation

国家自然科学基金项目(51209052)；黑龙江省青年科学基金资助项目(QC2011C013)；上海交通大学海洋工程国家重点实验室基金(1307)；国防预研项目(4010403010103)；中央高校基本科研业务费资助项目(HEUCF40117)；中国博士后基金(2014M552661)

2016-05-17 修改稿收到日期： 2016-09-09

庞福振 男，博士，副教授，1980年生

吴闯 男，博士生，1990年生

U661.44

A

10.13465/j.cnki.jvs.2017.22.021