基于改进HHT和马氏距离的齿轮故障诊断

周小龙， 刘薇娜， 姜振海； 马风雷

(1. 长春理工大学 机电工程学院， 长春 130022； 2. 长春工业大学 机电工程学院， 长春 130012)

基于改进HHT和马氏距离的齿轮故障诊断

周小龙1， 刘薇娜1， 姜振海2； 马风雷2

(1. 长春理工大学 机电工程学院， 长春 130022； 2. 长春工业大学 机电工程学院， 长春 130012)

针对齿轮振动信号非线性和非平稳的特点，提出一种基于改进希尔伯特-黄变换与马氏距离相结合的故障诊断方法。利用自适应白噪声的完备经验模态分解将齿轮振动信号分解成一系列固有模态函数，并采用敏感固有模态函数判别算法判断出对故障信息敏感的模态函数；通过对敏感固有模态分量的局部希尔伯特瞬时能量谱的分析，得出信号能量随时间变化的精确表达；以不同故障信号局部希尔伯特瞬时能量谱的最大峰值作为特征向量，采用马氏距离对齿轮故障进行状态识别。试验结果表明，该方法可有效识提取齿轮故障特征，实现不同故障状态识别。

齿轮；自适应白噪声完备经验模态分解；瞬时能量谱；马氏距离；故障诊断

齿轮是机械设备中的常用部件，而齿轮传动也是机械设备中常见的传动方式。通常，齿轮故障是导致机械设备失效的主要原因，因此，对齿轮进行故障诊断具有重要意义[1]。

当齿轮发生故障时，其振动信号往往是非线性、非平稳的时变信号，对于该类信号时频分析是有效的方法[2]。以经验模态分解(Empirical Mode Decomposition，EMD)为核心的希尔伯特-黄变换(Hilbert-Huang Transform，HHT)方法是近年来由Huang等[3]提出的一种处理非线性、非平稳信号的有效方法。然而在EMD分解过程中易产生模态混叠现象，这将影响EMD分解效果。为解决该问题，Wu等[4]提出了平均总体经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)方法，并被广泛应用于旋转机械的故障诊断中。李辉等[5]提出一种基于EEMD和Teager-Huang变换的齿轮箱故障诊断方法；张超等[6]采用EEMD和支持向量机相结合的方法对齿轮故障进行了有效诊断；吴小涛等[7]针对轴承振动信号的特点，提出了基于峭度准则EEMD和改进形态滤波方法的轴承故障诊断方法。虽然基于EEMD的HHT方法在机械故障诊断中取得了一定成果，但该方法仍然存在不足，并限制该方法在故障诊断领域的发展。其主要表现为：①EEMD分解后的固有模态函数(Intrinsic Mode Function，IMF)内仍有一定幅值的噪声残留，运算过程中选择加入白噪声的幅值和分解次数将直接影响着分解结果，如果参数选择不合理，将会降低分解效率，并使分解结果中会产生较多虚假IMF[8-9]。②EEMD分解出的IMF中，只有部分IMF能够反映故障特征，而其它的为干扰成分，如果干扰成分不剔除，将会影响HHT的故障诊断精度。

针对上述问题，提出一种基于自适应白噪声的完备经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN)局部Hilbert瞬时能量谱和马氏距离相结合的故障诊断方法。首先，利用CEEMDAN将非平稳的齿轮振动信号分解成一系列IMF，并采用敏感IMF判别算法判断出对故障信息敏感的IMF；其次，根据HHT方法的基本原理构建出敏感IMF分量的局部Hilbert瞬时能量谱，用于提取故障特征；最后，利用马氏距离对齿轮故障状态进行识别。试验结果表明：该方法可有效识别齿轮故障状态。

1 改进的HHT

1.1 CEEMDAN

相较于EEMD方法，CEEMDAN在分解过程中，采用对加入高斯白噪声进行EMD分解的方法代替EEMD分解过程中每次加入的高斯白噪声，可实现自适应加噪[10]，并能在较少平均次数下，实现重构误差几乎为零[11]。因此，CEEMDAN不仅能够克服EMD的模态混叠问题，同时能够提高分解效率，减少虚假IMF的产生。

步骤1与EEMD方法相同，在待分解信号x(t)中加入不同幅值的高斯白噪声ωi(t)，并进行I次分解。由EEMD对信号x(t)+ε0ωi(t)分解出的第1个IMF分量即为CEEMDAN的第1个模态分量。

步骤2在第一阶段(k=1)，计算第1个残余信号

(1)

步骤3对信号r1(t)+ε1E1(ωi(t)) (i=1,2,…,I)进行i次分解，直到得到第1个EMD模态分量为止，并计算第2个模态分量

(2)

步骤4对其余每个阶段(k=2,…,K)(i=1, 2,…,I)计算第k个残余信号

(3)

步骤5分解x(t)+εkEk(ωi(t))(i=1,2,…,I)～第1个EMD模态分量，并定义第k+1个模态分量为

(4)

步骤6执行步骤4，并将k+1。当残余信号的极值点个数不超过2个的时候分解结束。

分解结束时，设所有模态分量的数量为K，则最终的残差信号为

(5)

因此，原信号经CEEMDAN分解后可表示为

(6)

由CEEMDAN分解过程可知，其分解过程相对于EEMD更加完整，能够对待分解进行精确重构。在每一个模态分解阶段，根据系数εk可实现信噪比的自主选择。

为验证CEEMDAN的有效性，仿真一个由正弦波和冲击成分组成的信号。分别使用EEMD和CEEMDAN对仿真信号进行分解，分解过程中加入的白噪声标准差为0.2，分解次数500次，分解结果如图1和图2所示。由图1和图2可知，EEMD和CEEMDAN都将正弦信号和冲击信号分解出来，但由于参数选择问题，EEMD分解结果中出现了较多虚假IMF分量。而CEEMDAN有效减少了虚假IMF分量的产生，提高了分解准确性。

(a)仿真信号 (b)IMF1 (c)IMF2

(d)IMF3 (e)IMF4 (f)IMF5图1 EEMD分解结果Fig.1 EEMD decomposition results

(a)仿真信号 (b)IMF1 (c)IMF2 (d) IMF3图2 CEEMDAN分解结果Fig.2 CEEMDAN decomposition results

图3为EEMD和CEEMDAN两种分解方法的重构误差。由图3可知，CEEMDAN的重构误差小于10-15，而EEMD由于受到参数选择的影响，出现较大重构误差。因此，EEMD在一定程度上影响了信号分解的完整性，若想减小重构误差，需要提高分解次数，但这将导致计算规模的增加并降低计算速率。

(a)EEMD重构误差 (b) CEEMDAN重构误差图3 不同分解方法的重构误差Fig.3 Reconstruction error of different decomposition methods

1.2 敏感IMF判别算法

信号经CEEMDAN分解最终得到一系列IMF，虽然CEEMDAN能够有效减少虚假IMF分量的产生，但对于机械故障诊断而言，虚假IMF会影响故障诊断的准确性，同时，真实IMF中也只有部分IMF是包含故障特征或对故障特征敏感的。因此，在对IMF进行Hilbert变换前，需判别各IMF分量与所诊断故障的相关程度，保证故障特征提取的精度与诊断的有效性。在此采用一种基于信号相关性的敏感IMF判断法[12]。具体算法如下:

(1)计算故障信号x(t)的各IMF分量c1(t),…，cn(t)与原信号x(t)的相关系数αi；

(2)计算故障信号x(t)的各IMF分量c1(t),…，cn(t)与正常状态信号y(t)的相关系数βi；

(3)由两个相关系数计算得到各IMF分量包含故障信息的敏感相关系数γi，记作

γi=|αi-βi| (i=1,2,…,n)

(7)

(4)计算各IMF的故障敏感系数

(8)

(9)

(6)判断出敏感系数差值最大值所对应的序号k，那么排序后的前k个IMF即为故障敏感的IMF。

对于该方法，其主要原理是：与故障信号x(t)相关系数越大的IMF分量，所包含信号x(t)的故障信息越多；计算与正常状态信号y(t)的相关系数βi，可知每个IMF分量中与故障信息无关的正常信息。敏感IMF判别方法将各IMF与故障信号的相关性同正常信号的相关性相结合，配合敏感系数，能突显出故障信息，削弱正常信息的影响。

对于旋转机械系统而言，当系统构件出现故障时，会产生瞬态冲击。图1中的仿真信号可以看成一故障信号，经CEEMDAN分解后，IMF1为故障特征成分，而IMF2为虚假分量，IMF3为正常状态信息。采用敏感IMF判别算法计算各相关系数和敏感系数，结果如图4所示。

图4 仿真信号的敏感IMF判别结果Fig.4 The sensitive correlation coefficient results of simulation signal

由图4可知，故障特征成分IMF1被准确判别出来，而虚假成分IMF2和含有正常状态信息成分的IMF3被剔除，表明该算法的准确性。

1.3 局部Hilbert瞬时能量谱

对CEEMDAD分解后的各敏感IMF分量进行Hilbert变换

(10)

构造解析信号

(11)

进一步可求出瞬时频率

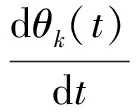
(12)

将上述敏感IMF的瞬时频率和瞬时幅值组合，可得信号的局部Hilbert谱

(13)

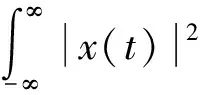
(14)

由此可以定义

(15)

式(15)为局部Hilbert瞬时能量谱(简称：局部瞬时能量谱)，它反映了信号能量随时间分布的情况。

常用的齿轮故障诊断方法一般基于振动能量的变化，但由于齿轮故障多为发生在各别齿上，所引起的振动能量变化在整个齿轮振动中所占比例较小，因此对于这种变化检测比较困难。当齿轮存在局部故障时，故障齿轮会产生较大的动载荷，并会影响到相邻齿，当故障程度增加时，动载荷增加，并会使振动能量发生较大变化。由敏感IMF求得的局部瞬时能量谱是对故障能量随时间变化的精确表示，可有效提取相关故障信息。

由之前分析可知，仿真信号的IMF1是敏感IMF，图5为其局部瞬时能量谱。在发生故障时，信号中的动载荷增加、振动加强，使相关时间段内信号的振动能量出现较大变化，结合时域信号特征，在振动开始和结束的阶段冲击最强。在图5中这些现象得到准确反映，显示出局部瞬时能量谱在故障特征提取方面的有效性。

图5 仿真信号的局部瞬时能量谱Fig.5 The local instantaneous energy spectrum of simulation signal

2 试验研究

为验证所提方法在故障特征提取方面的有效性，在齿轮试验台上进行了齿轮具有断齿、磨损和点蚀等三种故障的试验，其中断齿和点蚀故障发生在从动齿轮，磨损故障发生在驱动齿轮。试验所用的齿轮试验台型号为PQZZ-II型，图6为试验台装置图。

在齿轮故障模拟时，使用铁锤将齿轮故障实验台的从动齿轮的一个齿敲掉，折断线位于分度圆附近，用于模拟断齿故障；对另一从动齿轮的一个齿面进行点焊，并采用油石磨蚀使焊接残留的焊渣剥落，在其齿面上形成坑点，点蚀面积率为2%，用来模拟中等程度的点蚀故障；为模拟齿轮磨损故障，设置驱动齿轮的磨损为单齿齿面严重磨损，齿面磨损原因为人为磨锉，磨损程度为齿厚的15%。

图6 齿轮试验台Fig.6 Gear tester

试验过程中，电动机转频为50 Hz，对旋转机械而言，轴承座是设备易产生劣化现象的易损点，为保证所测数据的准确性，同时为全面监测齿轮箱的振动状态，加速度传感器安装在齿轮箱轴承座上。数据采集卡采用ADA16-8/2(LPCI)型高速多功能采集卡，设置采样频率为5 120 Hz，采样时间为1 s，采样精度为16 bt。平行轴齿轮箱中各齿轮均为标准直齿轮，其主要参数如表1所示。

表1 平行轴齿轮箱参数

试验采集到的各种状态条件下齿轮加速度信号如图7所示。从图7可知，在信号采集过程中，背景噪声较强，而由于没有消噪室，使信号的信噪比降低，这将影响改进HHT分析的准确性，同时增加故障检测难度。为此，采用快速独立分量分析(Fast Independent Component Analysis，FastICA)法对时域信号进行降噪处理，降噪后信号如图8所示。

(a)齿轮正常状态信号 (b)齿轮断齿故障信号 (c)齿轮磨损故障信号 (d)齿轮点蚀故障信号图7 齿轮振动信号Fig.7 Gear vibration signals

(a)齿轮正常状态降噪信号 (b)齿轮断齿降噪信号 (c)齿轮磨损降噪信号 (d)齿轮点蚀降噪信号图8 降噪后齿轮振动信号Fig.8 Noise reduction gear vibration signals

从图8可知，环境噪声等因素对于信号的干扰已得到明显改善。大部分的无用高频分量被滤去，降噪信号的波形更加突显出原信号的信息。各种齿轮故障信号在时域中均表现为脉冲冲击，同高斯幅值调制信号相类似。虽然不同故障的时域信号存在差异，但是以此为依据不能准确区分故障类型。采用基于CEEMDAN和敏感IMF的改进HHT方法对降噪后齿轮故障信号进行分析，3类故障信号经CEEMDAN分解后，断齿信号得到6个IMF分量，齿轮磨损和点蚀信号分别得到5个IMF分量。根据敏感IMF判别算法，计算各故障类型IMF分量的相关系数(αn，βn)和敏感系数(λn),如图9所示，通过敏感IMF判别算法，选择断齿信号的IMF1、磨损信号的IMF1和点蚀信号的IMF1 ～ IMF3为敏感IMF分量。各故障信号中其它IMF分量中所包含的是正常信号与故障信号的共同信息，所以将它们剔除。

(a)齿轮断齿信号的敏感IMF判别结果 (b)齿轮磨损信号的敏感IMF判别结果 (c)齿轮点蚀信号的敏感IMF判别结果图9 故障信号的敏感IMF判别结果Fig.9 The sensitive correlation coefficient results of fault signals

对齿轮各状态下的敏感IMF分量进行Hilbert变换，相应的局部瞬时能量谱,如图10所示。从图10可知，相较于齿轮正常啮合信号，各故障信号的局部瞬时能量谱具有明显的冲击特征，由于齿轮存在故障，这将导致齿轮在啮合过程中产生瞬态冲击的较大能量，不同故障类型所产生的瞬态冲击能量的大小也不相同。对各状态下信号的局部瞬时能量谱分析可知，当齿轮正常啮合时，局部瞬时能量谱有4个主要峰值，峰值均值为55.75，其中最大峰值为70；齿轮断齿状态下有4个主要峰值，其平均值为568.25，其中最大峰值为762； 齿轮磨损状态下有3个主要峰值，其平均值为2 430.47，其中最大峰值为3 752；齿轮点蚀状态下有4个主要峰值，其平均值为1 024.21，其中最大峰值为1 315。由上述分析可知，对于齿轮各种状态信号而言，瞬时能量谱峰值的最大值和均值存在明显差别，可将其作为故障特征进行诊断研究。

(a)齿轮正常信号局部 (b)齿轮断齿信号局部 (c)齿轮磨损信号局部 (d)齿轮点蚀信号局部 瞬时能量谱 瞬时能量谱 瞬时能量谱 瞬时能量谱图10 齿轮不同状态的局部瞬时能量谱Fig.10 Local instantaneous energy spectrum of different gear conditions

3 马氏距离的故障诊断分类

马氏距离是多元数理统计理论中常用的判别方法之一，用于表示数据的协方差距离。该方法的计算是建立在总体样本的基础上，排除了变量之间相关性的干扰，是一种衡量两个未知样本集相似程度的有效方法[13]。由于算法简单，并适用于小样本问题的处理，因此，被广泛应用于故障诊断[14]领域。

根据上节分析，选择不同状态下齿轮瞬时能量谱的最大值作为训练样本S进行马氏距离分析，具体步骤如下：

步骤1在齿轮故障综合诊断实验台上分别获取四种工况各30组数据；

步骤2为消除背景噪声对于故障诊断准确性的影响，采用FastICA降噪；

步骤3对降噪后各个样本信号进行改进HHT分析，得到瞬时能量谱；

步骤4以瞬时能量谱的最大值作为训练样本S；

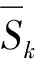
步骤6对待测齿轮故障信号x(t)按步骤2和步骤3求出其待测特征值Sx;

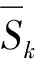
(16)

式中,k=1,2,3,4；分别代表齿轮正常、磨损、断齿和点蚀四种工作状态。

步骤8比较d1、d2、d3和d4的大小，并将最小判别距离所对应的状态作为待测信号的故障类型。

基于局部瞬时能量谱和马氏距离的齿轮故障诊断法流程图，如图11所示。

图11 齿轮故障诊断方法流程Fig.11 The technology process of gear fault diagnosis method

试验表明：通过小样本即可实现对齿轮故障的识别，对于未知样本的分类速度和识别准确率都较高，40组数据中出现了2组误判，总体识别正确率为95%。而误判数据的产生可能是由于测量过程中的测量误差和各种干扰因素的影响。部分识别结果如表2所示。表2部分识别结果

表2 部分识别结果

按上述方法，分别对制动力矩的输出电流在0.1 A和0.2 A工况条件下的60组数据进行识别，识别结果与实际故障类型基本一致，其中正常状态全部识别正确，磨损和断齿故障各有1组识别错误，齿轮点蚀有2组识别错误，总体诊断正确率为93.33%，进一步表明该方法的有效性。

4 结 论

(1)利用CEEMDAN分析信号，不但能够克服EMD分解过程中出现的模态混叠现象，同时可以解决EEMD分解效率低的问题。

(2)通过敏感IMF算法可以有效剔除与故障信息无关的IMF，增加故障特征提取的准确性。

(3)Hilbert瞬时能量谱能够准确反映出齿轮故障振动信号的能量随时间的分布情况，利用Hilbert瞬时能量谱可以较好的提取出齿轮故障信号的特征。

(4)基于改进HHT瞬时能量谱和马氏距离的故障诊断方法可以有效识别齿轮的故障状态，满足齿轮故障诊断要求，同时，实际应用时应尽量排除各种干扰因素，保证数据样本的数量。

[ 1 ] 于德介，程军圣，杨宇. Hilbert-Huang 变换在齿轮故障诊断中的应用[J]. 机械工程学报， 2005，41(6)： 102-107.

YU Dejie，CHENG Junsheng，YANG Yu. Application of Hilbert-Huang transform method to gear fault diagnosis[J]. Chinese Journal of Mechanical Engineering, 2005，41(6)： 102-107.

[ 2 ] 程军圣，杨宇，于德介. 局部均值分解方法及其在齿轮故障诊断中的应用[J]. 振动工程学报，2009，22(1)： 76-84.

CHENG Junsheng，YANG Yu，YU Dejie. The local mean decomposition method and its application to gear fault diagnosis[J]. Journal of Vibration Engineering, 2009，22(1)： 76-84.

[ 3 ] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceeding of the Royal Society of London-Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.

[ 4 ] WU Z, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.

[ 5 ] 李辉，郑海起，唐力伟. 基于EEMD 和THT 的齿轮故障诊断方法[J]. 振动、测试与诊断，2011，31(4)： 496-500.

LI Hui，ZHENG Haiqi，TANG Liwei. Gear fault diagnosis method based on EEMD and THT [J]. Journal of Vibration，Measurement amp; Diagnosis, 2011，31(4)： 496-500.

[ 6 ] 张超，陈建军，郭迅. 基于EEMD能量熵和支持向量机的齿轮故障诊断方法[J]. 中南大学学报(自然科学版)，2012，43(3)： 932-939.

ZHANG Chao，CHEN Jianjun，GUO Xun. Gear fault diagnosis method based on ensemble empirical mode decomposition energy entropy and support vector machine[J]. Journal of Central South University (Science and Technology), 2012，43(3)： 932-939.

[ 7 ] 吴小涛，杨锰，袁晓辉，等. 基于峭度准则EEMD及改进形态滤波方法的轴承故障诊断[J]. 振动与冲击，2015，34(2)： 38-44.

WU Xiaotao, YANG Meng, YUAN Xiaohui, et al. Bearing fault diagnosis using EEMD and improved morphological filtering method based on kurtosis criterion [J]. Journal of Vibration and Shock, 2015，34(2)： 38-44.

[ 8 ] TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise [C] // IEEE International Conference on Speech and Signal Processing. Prague: ICASSP, 2011: 4144-4147.

[ 9 ] COLOMINAS M A, SCHLOTTHAUER G, TORRES M E. Improved complete ensemble EMD: a suitable tool for biomedical signal processing [J]. Biomedical Signal Processing amp; Control, 2014, 14(1): 19-29.

[10] 韩庆阳，孙强，王晓东，等. CEEMDAN去噪在拉曼光谱中的应用研究[J]. 激光与光电子学进展，2015，52(11)： 267-274.

HAN Qingyang，SUN Qiang，WANG Xiaodong，et al. Application of CEEMDAN in Raman spectroscopy denoising[J]. Laser amp; Optoelectronics Progress, 2015，52(11)： 268-274.

[11] 李军，李青. 基于CEEMDAN-排列熵和泄漏积分ESN的中期电力负荷预测研究[J]. 电机与控制学报，2015，19(8)： 70-80.

LI Jun，LI Qing. Medium term electricity load forecasting based on CEEMDAN-permutation entropy and ESN with leaky integrator neurons[J]. Electric Machines and Control, 2015，19(8)： 70-80.

[12] 雷亚国. 基于Hilbert-Huang变换的机械故障诊断[J]. 机械工程学报，2011，47(5)： 71-77.

LEI Yaguo. Machinery fault diagnosis based on improved Hilbert-Huang transform[J]. Journal of Mechanical Engineering, 2011，47(5)： 71-77.

[13] 刘昱，张俊红，毕凤荣，等. 基于LMD边际谱的柴油机气门故障诊断[J]. 内燃机学报，2014，35(6)： 96-100.

LIU Yu，ZHANG Junhong，BI Fengrong，et al. Diesel engine valve fault diagnosis based on LMD marginal spectrum[J]. Chinese Internal Combustion Engine Engineering, 2014，35(6)： 96-100.

[14] 骆志高，李旭东，赵俊丽，等. 利用马氏距离判别法准确实现对裂纹的识别[J]. 振动与冲击，2013，32(21)：186-188.

LUO Zhigao, LI Xudong, ZHAO Junli, et al. Crack identification with mahalanobis distance discrimination method [J]. Journal of Vibration and Shock, 2013，32(21)：186-188.

GearfaultdiagnosisbasedonimprovedHHTandMahalanobisdistance

ZHOU Xiaolong1， LIU Weina1， JIANG Zhenhai2， MA Fenglei2

(1. College of Mechanical and Electric Engineering, Changchun University of Science and Technology, Changchun 130022, China; 2.School of Mechatronic Engineering, Changchun University of Technology, Changchun 130012, China)

In view of nonlinear and non-stationary characteristics of gear vibration signals, a fault diagnosis method based on improved Hilbert-Huang transform and Mahalanobis distance was proposed. The gear vibration signals were decomposed by complete ensemble empirical mode decomposition with adaptive noise, the intrinsic mode functions were obtained and sensitive intrinsic mode functions were selected by the sensitivity evaluation method. Then, the local Hilbert instantaneous energy spectrum of the sensitive intrinsic mode components was analyzed, and the fault information can be extracted from the distribution of the energy of the gear vibration signal with the change of time. Finally, the maximum peak value of the local Hilbert instantaneous energy spectrum was treated as the fault features and the Mahalanobis distance method was used for judging the gear fault. Experimental results show that the method can effectively extract gear fault features and apply for different fault identification.

gear; complete ensemble empirical mode decomposition with adaptive noise; instantaneous energy spectrum; Mahalanobis distance; fault diagnosis

国家自然科学基金资助项目(51075041)；吉林省教育厅科技发展项目(2014124)

2016-05-11 修改稿收到日期： 2016-09-20

周小龙 男，博士生，1987年生

刘薇娜 女，博士，教授，1956年生

TH17

A

10.13465/j.cnki.jvs.2017.22.034