应用动态数学技术丰富学生数学活动经验*

☆ 张 薇 杨秀燕 唐剑岚

（广西师范大学数学与统计学院，广西桂林 541004）

应用动态数学技术丰富学生数学活动经验*

☆ 张 薇 杨秀燕 唐剑岚

（广西师范大学数学与统计学院，广西桂林 541004）

互联网+动态数学技术已经成为改善传统数学教学、提效学生数学学习的利器。恰当使用动态数学技术可以丰富学生数学活动经验、丰富直观感知、强化动手操作、助力猜想验证、促进本质理解和改善学习方式。

动态数学技术；数学活动经验

《普通高中数学课程标准(实验)》(以下简称《标准》)提倡注重信息技术与数学课程的整合[1]。互联网+动态数学技术已经成为改善传统数学教学、提效学生数学学习的利器。动态数学技术是指应用诸如Hawgent皓骏、玲珑画板、图形计算器等动态数学软件改善数学教学的技术。恰当使用动态数学技术可以丰富学生数学活动经验：丰富直观感知、强化动手操作、助力猜想验证、促进本质理解和改善学习方式。

一、丰富直观感知

直观感知是学习和理解数学的基本途径。研究表明，如果仅仅运用语言、板书、课本上的文字等言语化表征，教师是难以传达三维或以上数学对象的。即便运用图形、图表等静态表征加以阐释，学生也可能难以理解[2]。动态数学技术能将抽象言语化表征、静态图形表征动态视觉化，直观可见地呈现数学学习对象的微观结构与过程，揭示动态变化中蕴含不变的数学关系，不仅丰富学生的直观感知和想象，也可以促进学生对数学对象的理解。

譬如：让学生直观感知椭圆、双曲线、抛物线等圆锥曲线的形成，在现实教学中是一个难点。但如果应用动态数学软件设计积件（如图1），并动态演示圆锥曲线的形成过程，不仅能丰富学生的直观感知，也有助于理解圆锥曲线的定义。

图1 应用动态数学软件设计的积件

二、强化动手操作

动手实践是学生学习数学的重要方式之一[1]。然而在现实课堂中，“教师操作为主，学生有参与没体验”的低效甚至无效的动手实践现象仍时有发生。如果以学生操作为主，也许能有效提高学生动手实践的实效性。

譬如：“探究函数 Y=Asin(ωx+φ)的图象与性质”这堂课，理解参数变化对函数图象变化的影响是教学难点。传统教学只能赋有限个数值给A、ω、φ画出图象，这样既耗时又失一般性。如果借助动态数学软件设计积件（如图2），首先让学生动手操作，通过拖动变量点亲自感受单个参数A、w、j分别影响着函数Y=sinx图象的伸缩、平移变换；接着，引导学生进一步探究由Y=sinx的图象得到Y=sin(x+φ)的图象，再得到的图象，最后得到的图象，函数图象经历怎样的变化过程；最后，改变变换的顺序，进一步明晰各参数对函数图象变换的影响。这样设计不仅渗透数形结合的思想，同时让学生在动脑的同时动手“做”数学，主动建构知识，感悟学习成就，从而达到“授人以鱼的同时授人以渔与欲”的目标[3]。

图2 函数Y=Asin(ωx+φ)的图象变换

三、助力猜想验证

猜想验证是学习和研究数学的重要活动，是学生由感性经验上升至理性经验的一个重要过程。动态数学技术为学生进行猜想验证提供了可操作的实验环境。学生在依据已有的具体事实、感性经验的基础上提出猜想或假设后，可借助Hawgent皓骏等动态数学技术，不仅能提升验证猜想的效力，而且有助于在“想中做”、“做中思”的过程中进一步内化知识。

譬如：在“探究底数a对指数函数y=ax(a＞0且|a|≠1)图象变化的影响”的教学中，传统教学一般让学生动手绘制底数a取特定值时的指数函数图象，再引导学生运用数形结合的思想，直接总结归纳变化规律。这样教学较难破解“底数a是影响图象变化的根源”这个教学难点。如果利用动态数学软件设计积件（如图3），利用参数a动态演示指数函数的图象变化，实现数、符号、图象多元表征联系，不仅能助力验证猜想，而且可促进学生理解指数函数的性质。

图3 指数函数的图像变化

四、促进本质理解

研究表明，良好的视觉化表征具有很强的启发性[2]。动态数学技术能通过数字、符号、图形或图表多元表征数学对象，直观凸显数学对象的多元联系，帮助学生建立表征间的联系和转译，促进对数学本质的理解。

譬如：在导数的几何意义教学时，借助动态数学软件设计积件（如图4）。首先，利用几何直观启发学生发现平均变化率在图形中表示割线AB的斜率；接着，拖动变量尺使点A沿函数图象逼近点B，引导学生结合几何和代数知识，发现此时割线AB无限趋近于点B处的切线，从而得出导数的几何意义。这样设计，让学生从数值逼近，几何直观感受，解析式抽象多种方式理解，有利于学生数形结合感知割线逼近切线的变化过程，消除对极限的神秘感，加强知识间的联系，促进学生深入理解导数的几何意义。

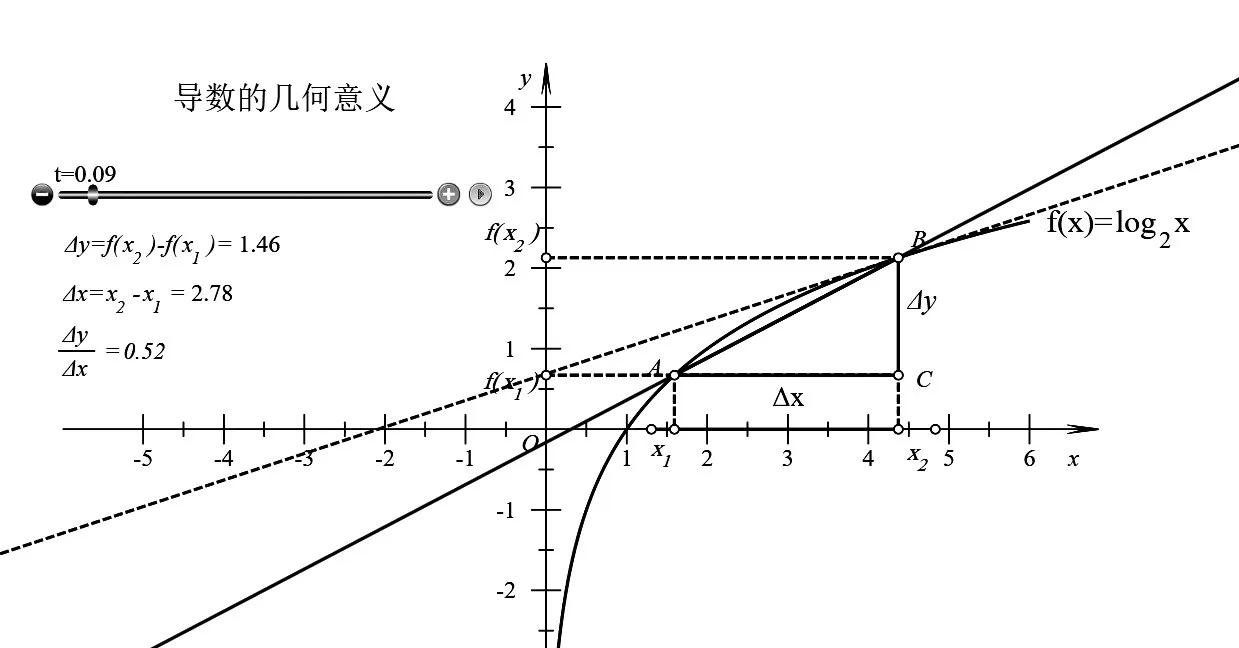
图4 导数的几何意义

五、改善学习方式

动态数学技术给数学学习赋予了新的内涵和生命力，为学生提供更多自主探索、动手实践、合作交流、阅读自学的机会，从而在潜移默化中改善学生的学习方式。其主要体现在以下两个方面。

化被动接受为主动探究，亲历知识发生、发展的过程。动态数学软件为学生建构了研究性学习的新模式，让学生亲历实验探究的过程。在课堂上，学生不再只是旁观者或听众，而是课堂的主动参与者。由于亲自动手实践，学生更容易对实验结果、产生结果的原因等产生强烈的好奇心，从而激发学生主动探求新知的欲望，实现知识的主动建构。同时让学生经历设计实验、操作实验、分析实验结果的过程，更有助于培养学生发现问题、分析问题、解决问题的能力。

为学生提供个性化学习工具，优化学习过程。例如：与图形有关的动点问题是涉及函数、几何、运算等的综合题型，是高中学生解题过程中常见的拦路虎。部分学生因无法想象图形运动的变化规律，从而产生畏难心理。动态数学软件中的图形计算器不只是教师演示的工具，也是学生个性化的学习工具[4]。学生可用于答疑解惑，检验正误，有利于提高学生的自我效能感，改善数学学习信念[5]；再如，玲珑画板的3D功能为学生探究立体几何提供更广阔的探究空间，有助于培养学生数学抽象、空间想象的数学核心素养等。

[1]中华人民共和国教育部制订.普通高中数学课程标准（实验）[M].北京：人民教育出版社,2003,9.

[2]唐剑岚.数学多元表征学习及教学[M].南京：南京师范大学出版社,2009.

[3]唐剑岚,周元.“授人以鱼”的同时“授人以渔与欲”—以《等差数列的前n项和》公式推导片段为例[J].数学通报,2016,(09)：41-46.

[4]王长沛.图形计算器：不可替代的“数学工具”[J].中小学信息技术教育,2007,(03)：111-120.

[5]唐剑岚,蒋蜜蜜,肖宝莹.数学认识信念：影响数学学习过程的重要变量[J].课程·教材·教法,2014,(06).

本文为以下项目成果：广西普通高中学科基地建设项目;2017年广西研究生教育创新计划项目（XYCSZ2017073）的部分成果。

[编辑：刘睿]

G434

A

1671-7503（2017）21-0055-03