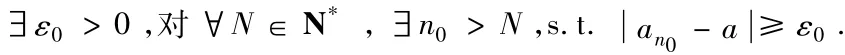数列极限的否命题教学设计

李 辉 安黔江(铜仁学院大数据学院数学与统计系 贵州 铜仁 554300)

1 数列极限的正面命题如下:

笔者在教学时发现学生对否命题理解不充分，改为其否命题时不熟练．众所周知，对极限语言体系的理解会决定学生的学习水平。对于将正命题改为否命题如果化为以下几个步骤，则使学生理解容易，而且过渡自然。

2 改为否命题的几个启发性问题及其关键步骤．

对ε＞0，满足性质P，叫做概念A．(其中性质P表示:-N∈N*，s．t．当 n ＞ N 时，有＜ ε;性质 P1表示:s．t．当 n ＞ N时，有＜ε;概念A表示:数列 { an}的极限是a．)

问:如果不叫概念A，应该如何表述?应该这样表述:

-ε0＞0，不满足性质P，则不叫概念A．

问:什么叫不满足性质P?(每当如此发问时，给予学生片刻思考时间)

不存在N，满足性质P1．

问:什么叫不存在N，满足性质P1?

就是对N而言，在大于N之后的所有n，有些n能满足性质P1，但还有些n不能满足性质P．

问:什么叫做有些n能满足性质P1，但还有些n不能满足性质P?

就是-n0＞ N，s．t．ε0

总结起来就是: