基于ALIF-HT的汽轮发电机组转子故障诊断
2017-11-28唐贵基
唐贵基, 庞 彬
(华北电力大学 能源动力与机械工程学院, 河北保定 071003)
基于ALIF-HT的汽轮发电机组转子故障诊断
唐贵基, 庞 彬
(华北电力大学 能源动力与机械工程学院, 河北保定 071003)
针对汽轮发电机组转子故障振动信号为多分量非平稳信号,将一种新的信号分解方法——自适应局部迭代滤波(ALIF)用于转子故障振动信号分解,并与希尔伯特变换(HT)相结合,提出了基于ALIF-HT的汽轮发电机组转子故障诊断方法:首先对转子原始振动信号进行ALIF得到若干信号分量,再应用HT求取每个分量的瞬时频率,获取原信号全部信号分量的完整时频表示,最后根据转子故障振动信号的时频特征判别转子的故障类型.通过仿真信号分析验证ALIF对多分量信号的分解能力,并利用转子油膜失稳故障分析验证该方法的工程实用性.结果表明:ALIF方法能够有效克服经验模态分解(EMD)存在的模态混叠问题,使得ALIF-HT方法相对于希尔伯特黄变换(HHT)方法具有更高的时频分析精度.
汽轮发电机组; 转子; 故障诊断; 自适应局部迭代滤波; 希尔伯特变换
转子作为汽轮发电机组的重要部件,对整个发电系统的安全运行具有重要影响.转子故障不仅会造成机组异响和振动过大,甚至会引发大的安全事故.因此,对汽轮发电机组转子故障进行诊断具有重大意义[1].
汽轮发电机组转子产生油膜涡动、油膜振荡、碰摩及不平衡等故障时,其振动信号通常为转频、转频谐波与现场噪声复合而成的多分量非平稳信号[2].由于时频分析可同时表达振动信号的时域和频域信息,因而在转子故障诊断中得到广泛应用[3].常用的时频分析方法有短时傅里叶变换[4]、小波变换[5]、魏格纳分布[6]及希尔伯特黄变换(HHT)[7]等.但上述时频分析方法均存在一定缺陷,如短时傅里叶变换时频窗固定,小波变换基函数选取缺乏自适应性,魏格纳分布虽然可保证较高的时频分辨率,但很难克服交叉项.HHT通过经验模态分解(EMD)方法对原信号进行分解,再利用希尔伯特变换(HT)提取各个分量的瞬时频率,具有良好的自适应性,被广泛应用于时频故障特征提取.但EMD方法提取信号分量的过程需要拟合包络线,容易出现过包络、欠包络和模态混叠问题[8-9].
借鉴HHT思路,众多学者对信号自适应分解方法展开了研究.本征时间尺度分解[10]、集合经验模态分解[11]、局部均值分解[12]和局部特征尺度分解[13]等方法被应用于转子故障诊断,这些方法在一定程度上解决了EMD存在的模态混叠问题,但信号提取过程中均用到了极值点拟合,会对分析精度产生很大影响.为此,Lin 等[14]提出了迭代滤波的信号分解方法,利用滤波函数代替EMD中值曲线的求解过程.为实现滤波函数的自适应选取,Cicone等[15]提出了自适应局部迭代滤波(ALIF)的信号分解方法,大大提高了信号分解精度.笔者将ALIF方法结合HT提出了基于ALIF-HT的汽轮发电机组转子故障诊断方法,通过仿真信号和转子故障诊断实例验证了该方法的有效性.
1 ALIF基本原理
自适应局部迭代滤波分解是在迭代滤波信号分解方法基础上提出的,二者不同之处在于ALIF方法Fokker-Planck方程实现了滤波函数的自适应选取,因此有必要先对迭代滤波的基本原理加以介绍.
1.1迭代滤波
与EMD方法相近,迭代滤波也是通过迭代筛选的方法来求取每个本征模态函数(IMF)分量的,该方法通过对原信号滤波构造滑动算子,代替EMD方法的中值曲线求解过程.迭代滤波主要包括内循环和外循环2个过程.
1.1.1 内循环过程
内循环过程的主要目的是构造滑动算子,然后迭代筛选每个IMF分量.对于连续时间信号x(t),滑动算子Γ(x(t))由x(t)与滤波函数w(t)卷积获得:
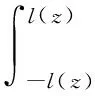
(1)
式中:w(t)为滤波区间为l(z)的固定低通滤波函数;t为时间;τ为时间延迟.
l(z)可通过下式计算获得:
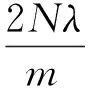
(2)
式中:N为信号的长度;m为待分解信号的极值点数目;λ∈[1,2],为可调参数,原信号信噪比越高,设置的λ值越大.
原信号与滑动算子相减可得到波动算子:
k(x(t))=x(t)-Γ(x(t))
(3)
若波动算子k(x(t))满足IMF条件,则k(x(t))可作为一个IMF分量被提取出来.但通常初次求得的波动算子k(x(t))不能满足IMF条件,需要对每次获得的波动算子进行迭代筛选,具体步骤如下.
(1) 利用式(2)计算待分解信号的滤波区间l(z).
(2) 根据式(1)计算滑动算子.
(3) 利用式(3)求解波动算子,为阐述清楚IMF分量的筛选过程,给出每次筛选的波动算子的计算表达式:
kn(x(t))=xn(t)-Γn(x(t))=xn+1(t)
(4)
式中:kn(x(t))为第n次筛选后的波动算子,且x1(t)=x(t).
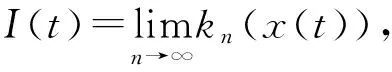

(5)
式中:ki,n为第i次筛选得到的波动算子.
当θ小于指定阈值时,筛选停止,提取的IMF分量记为I(t).
1.1.2 外循环过程
外循环用来终止内循环的IMF分量提取过程,内循环完成IMF分量提取后的余量信号记为r(t):
r(t)=x(t)-I(t)
(6)
当r(t)呈现明显的趋势特征时,整个迭代滤波过程结束.否则,将r(t)作为新的待分解信号执行内循环.
1.2基于Fokker-Planck方程的自适应局部迭代滤波
为实现迭代滤波过程中滤波函数的自适应选取,Cicone等根据不同滤波区间Fokker-Planck 方程的基础系构造具有自适应特点的滤波函数.Fokker-Planck方程的具体形式为:
Pt=-α(h(x)p)x+β(g2(x)p)xx,αgt;0,βgt;0
(7)
式中:h(x)和g(x)为2个光滑的可微函数,且在[a,b](其中alt;0lt;b)上满足g(a)=g(b)=0,∀x∈(a,b),g(x)gt;0;h(a) lt;0lt;h(b).
方程中(g2(x)p)xx项会产生扩散效果,并使方程的解p(x)从区间[a,b]中心向两端移动.(h(x)p)x项驱使p(x)从区间[a,b]两端向中心聚拢.当二者平衡时有:
-α(h(x)p)x+β(g2(x)p)xx=0
(8)
此时,方程的解p(x)且满足条件:∀x∈(a,b),p(x)gt;0且∀x∉(a,b),p(x)=0.
Fokker-Planck方程解p(x)即为构造的滤波函数w(t),w(t)随着[a,b]的改变求解出不同的表达式,由此实现ALIF对滤波函数的自适应求解.
2 ALIF-HT时频分析原理
ALIF-HT利用ALIF将原信号分解为一系列瞬时频率具有物理意义的IMF分量,再利用HT求解每个IMF分量的瞬时频率,可得到各个分量的时频表示,称为ALIF-HT时频分析.连续时间信号x(t)的HT定义为:
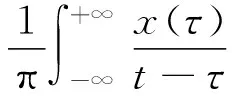
(9)
利用式(10)构造解析信号z(t):
z(t)=x(t)+jH(x(t))=a(t)ejφ(t)
(10)
于是得到幅值函数a(t)与相位函数φ(t):
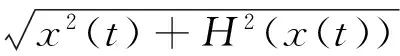
(11)

(12)
对相位函数求导得到瞬时频率ω(t):
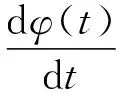
(13)
3 仿真分析
转子运行过程中经常会产生噪声与异常干扰问题,使得常规信号分解方法的分析效果受到严重影响.为此,通过设计2组仿真信号x1(t)和x2(t),分别验证噪声和异常干扰2种条件下ALIF对多分量非平稳信号的分解效果.2组仿真信号的表达式分别为:
x1(t)=x11(t)+x12(t)+x13(t)
(14)
x2(t)=x21(t)+x22(t)
(15)

仿真信号x1(t)由调幅调频信号x11(t)、调频信号x12(t)和随机噪声x13(t) 3个分量叠加而成.仿真信号x2(t)由正弦信号x21(t)和间断信号x22(t)叠加而成,其中x22(t)可以模拟高频异常干扰.x1(t)、x2(t)及其各自组成分量信号的时域波形如图1所示.分别对x1(t)和x2(t)进行自适应局部迭代滤波,分解产生的分量如图2所示.由图2可知,ALIF分别实现了噪声和异常干扰2种条件下对x1(t)、x2(t)各组成分量的分解,具有良好的分析精度.
为体现ALIF自适应分解方法的优越性,与EMD方法进行对比分析,图3(a)和图3(b)分别为EMD方法对x1(t)和x2(t)的分解结果.由图2和图3可知,EMD分解的分量出现了模态混叠现象和虚假分量;ALIF则有效抑制了模态混叠现象的发生,具有更高的分析精度.
4 转子油膜失稳故障分析
为进一步说明所述方法的工程实用性,在图4所示的Bently RK4转子实验台上模拟了油膜涡动和油膜振荡2种油膜失稳故障.该实验台由转速调节装置、前置适配器和轴承油泵系统构成.实验数据采集设备为美国Iotech公司生产的ZonicBook/618E,采样频率fs=1 280 Hz.
首先模拟2 800 r/min转速下转子的油膜涡动故障.油膜涡动是转子在油膜力作用下同时绕自身轴线和轴承中心线回转的一种运动形式.发生此类故障时,振动信号不仅包含转频成分,而且会产生涡动频率,由于涡动频率与转频二分频相近,油膜涡动通常又称为半频涡动.任选数据长度为2 048个点的油膜涡动故障振动信号(以下简称油膜涡动信号)进行分析,其时域波形如图5所示.该时域波形与正弦信号类似,仅从时域波形不能判断转子的故障类型.对油膜涡动信号进行ALIF分析,分解结果如图6(a)所示,利用HT方法进一步求解2个IMF分量的瞬时频率,得到图6(b)所示的ALIF-HT时频图.图6(b)中的2个瞬时频率分别为23 Hz和46.65 Hz,二者分别与涡动频率和转子转频对应,ALIF-HT时频图体现出显著的油膜涡动故障时频特征.



(a) x1(t)及其组成分量信号的时域波形
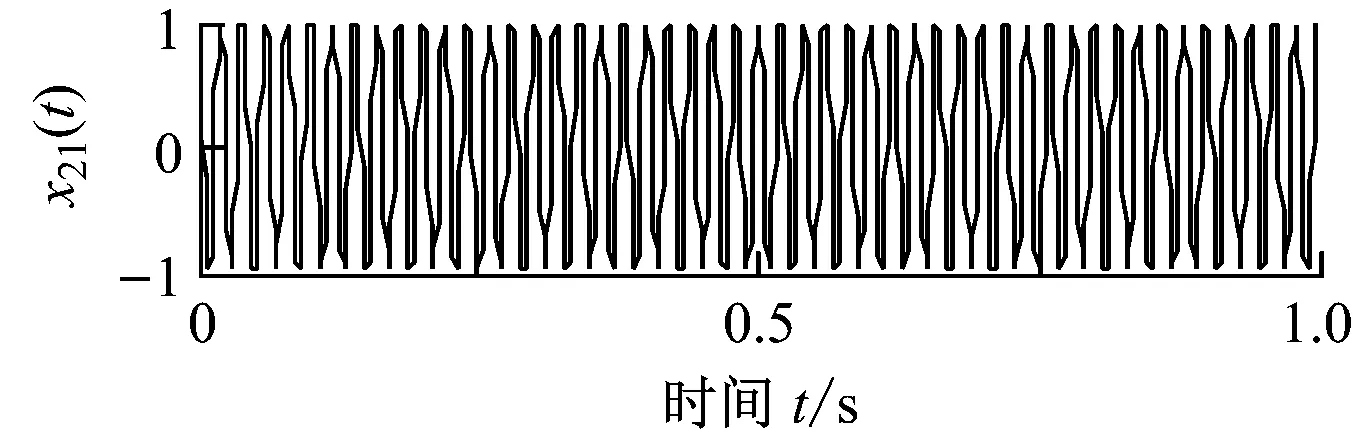
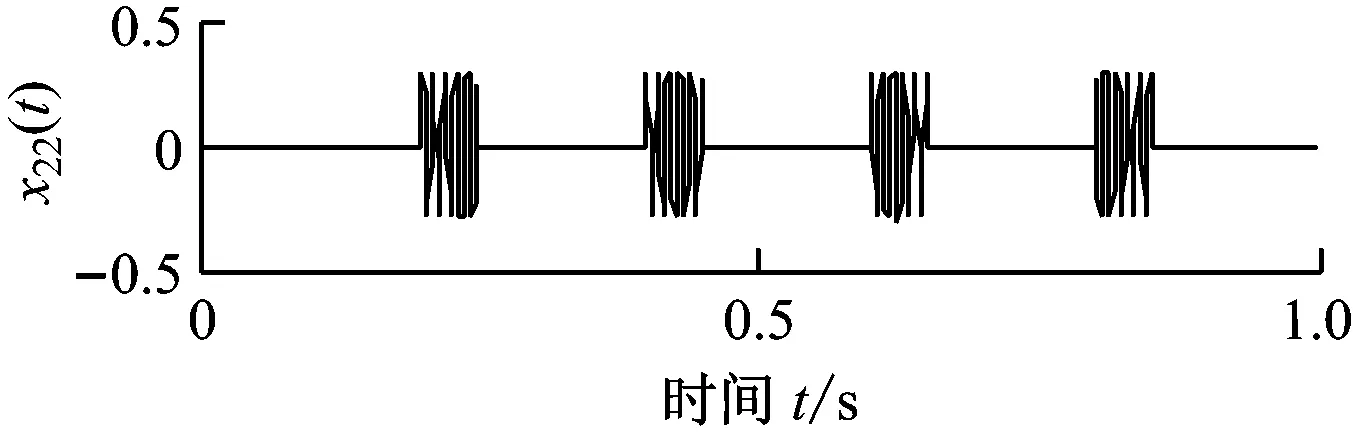
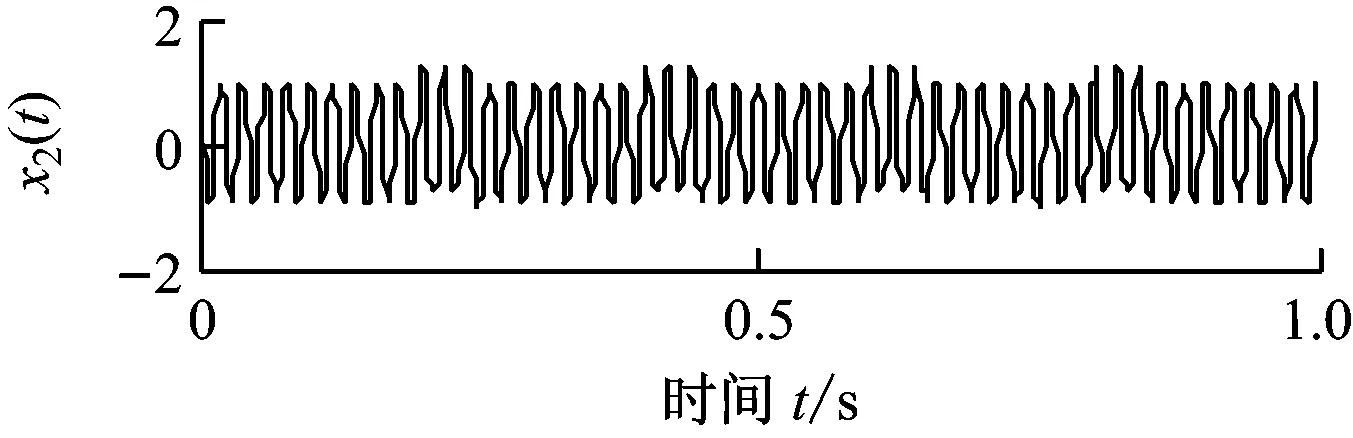
(b) x2(t)及其组成分量信号的时域波形图1 仿真信号及其组成分量信号的时域波形Fig.1 Time waveform of simulated signals and their components
图7(a)给出了油膜涡动信号的EMD分解结果.EMD分解产生的IMF2、IMF32个分量与油膜涡动信号的特征分量相近,但二者皆存在一定程度的模态混叠和波形畸变现象,求解EMD分解产生的各个IMF分量,得到HHT的分析结果,如图7(b)所示,涡动频率与转频之间存在交叉混叠现象.

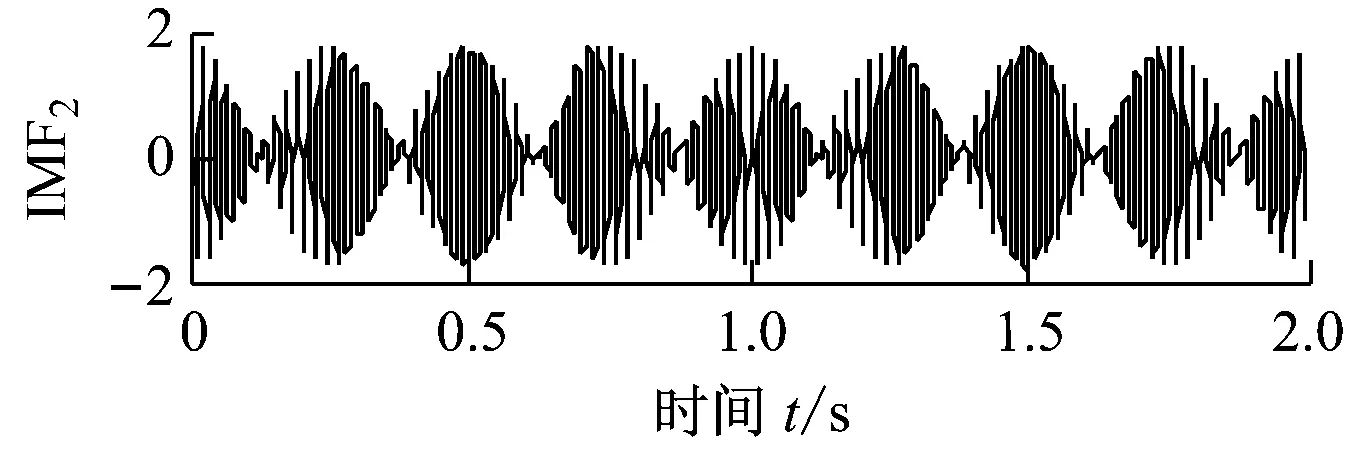
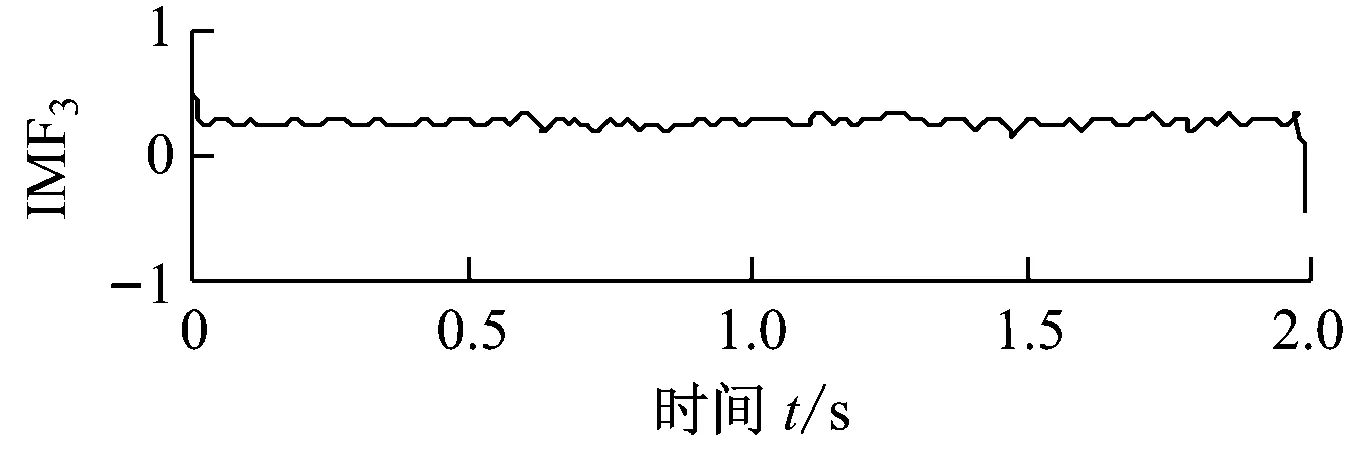
(a) x1(t)的ALIF分解结果

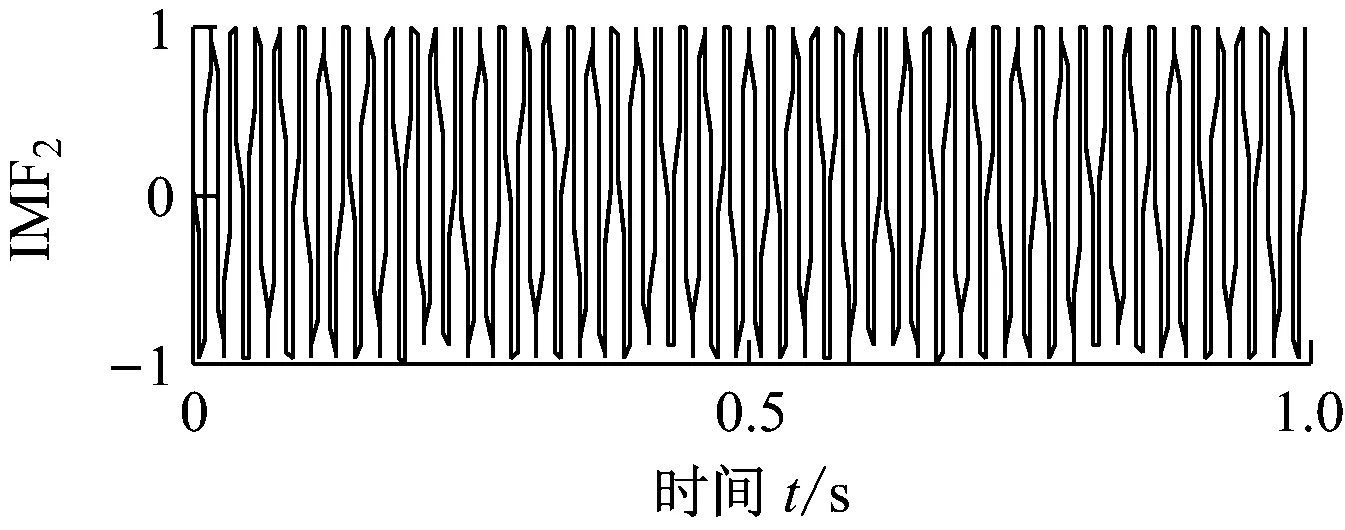
(b) x2(t)的ALIF分解结果图2 仿真信号的ALIF分解结果Fig.2 ALIF decomposition results of simulated signals
将转速升至4 500 r/min,转速达到实验台转子一阶临界转速2倍以上时,涡动频率接近转子的第一阶固有频率,油膜涡动演变为油膜振荡,本实验台的油膜振荡频率在31 Hz附近.图8给出了油膜振荡信号的时域波形,同样对油膜振荡信号进行ALIF分解,结果如图9(a)所示.图9(b)为本文方法获得的ALIF-HT时频图.图9(b)中2个频率分量的中心频率分别为30.6 Hz和75 Hz.ALIF-HT精确提取出了油膜振荡信号的时频特征.图10给出了油膜振荡信号的HHT分析结果.由图10可知,由于EMD分解分量存在模态混叠现象和无意义分量,使得HHT时频图的时频成分杂乱无章,不能提取出清晰的故障时频特征.

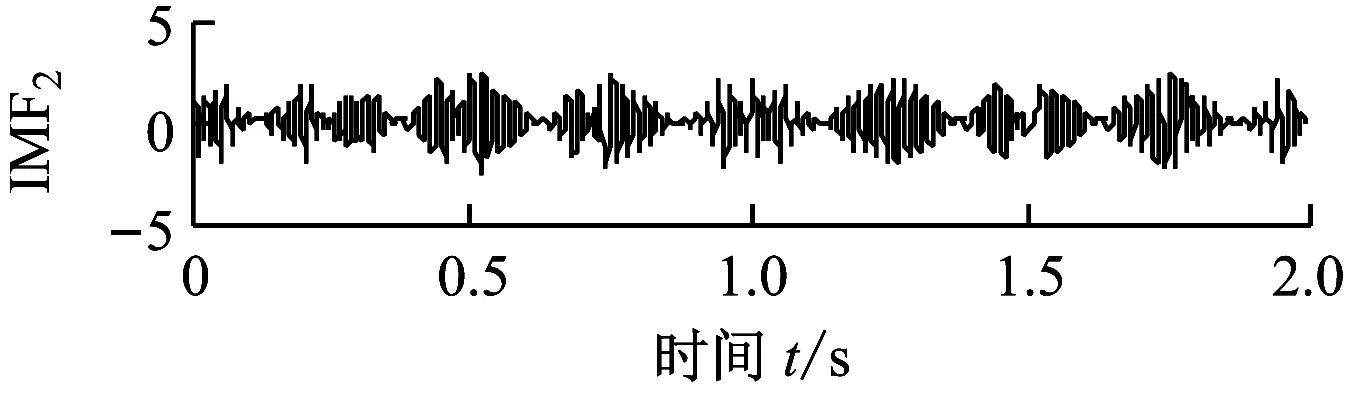
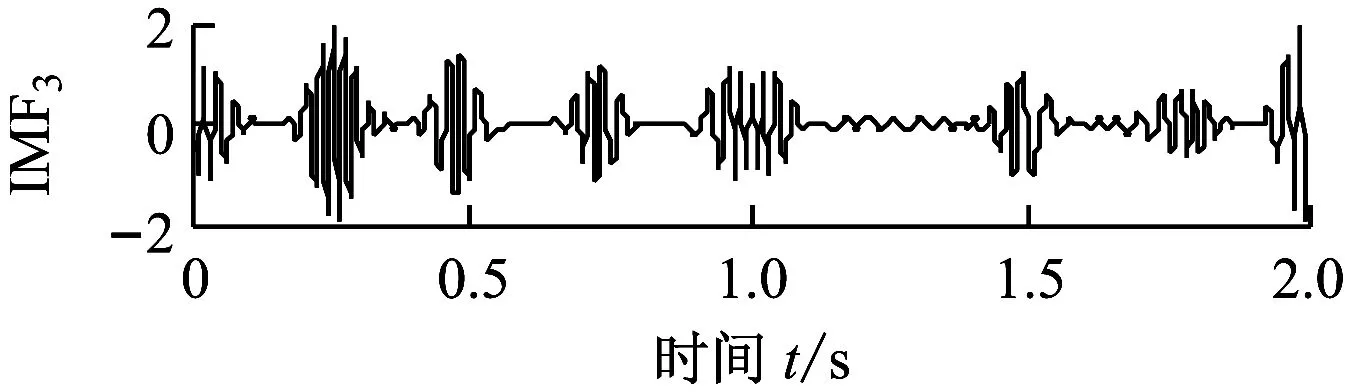
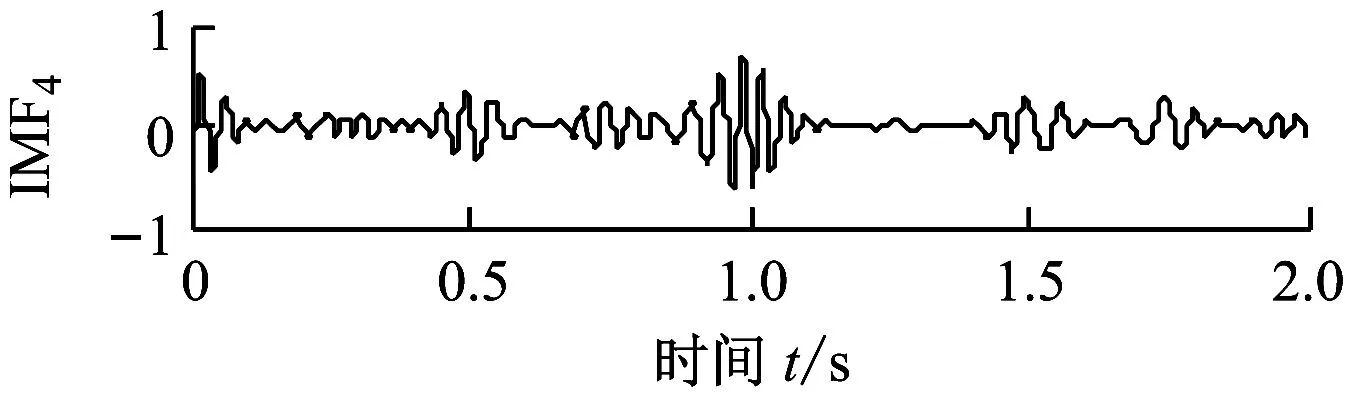
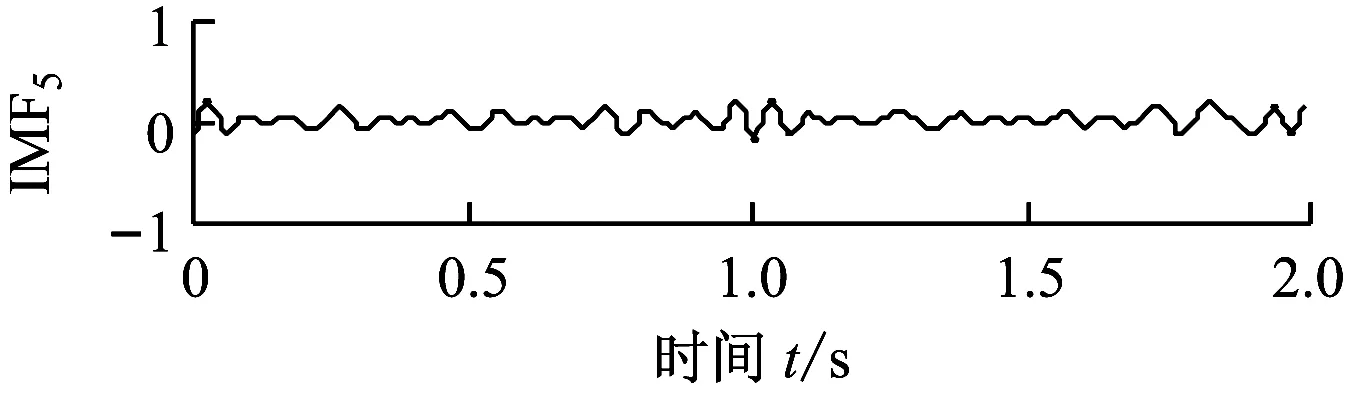

(a) x1(t)的EMD分解结果
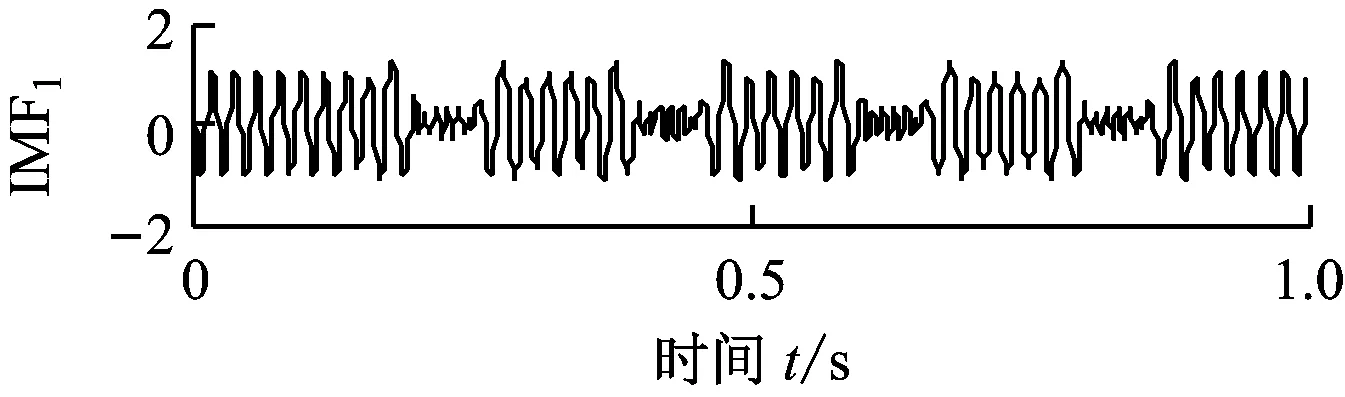

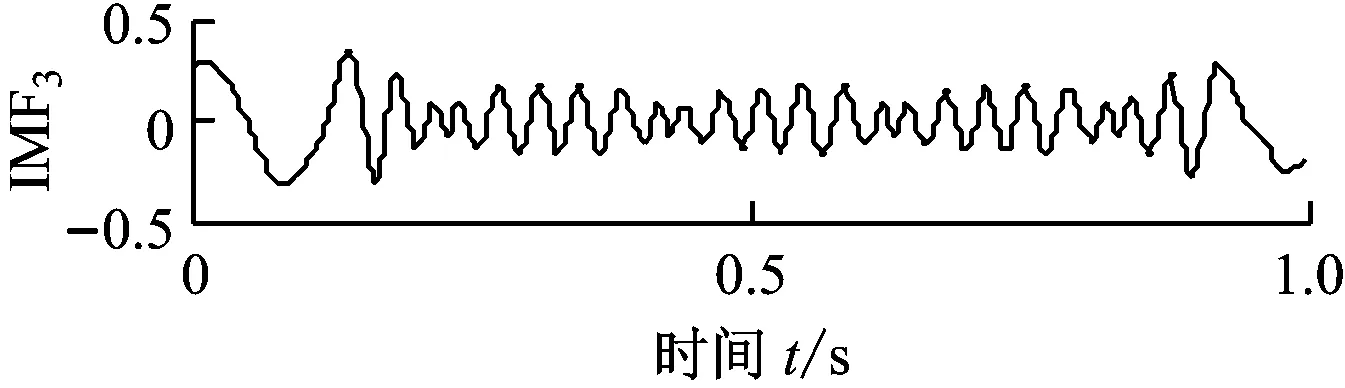
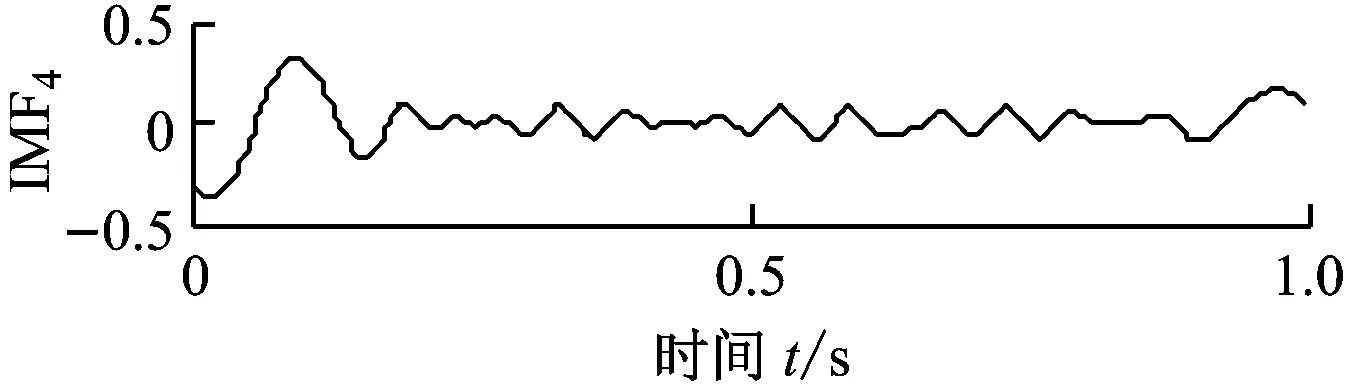
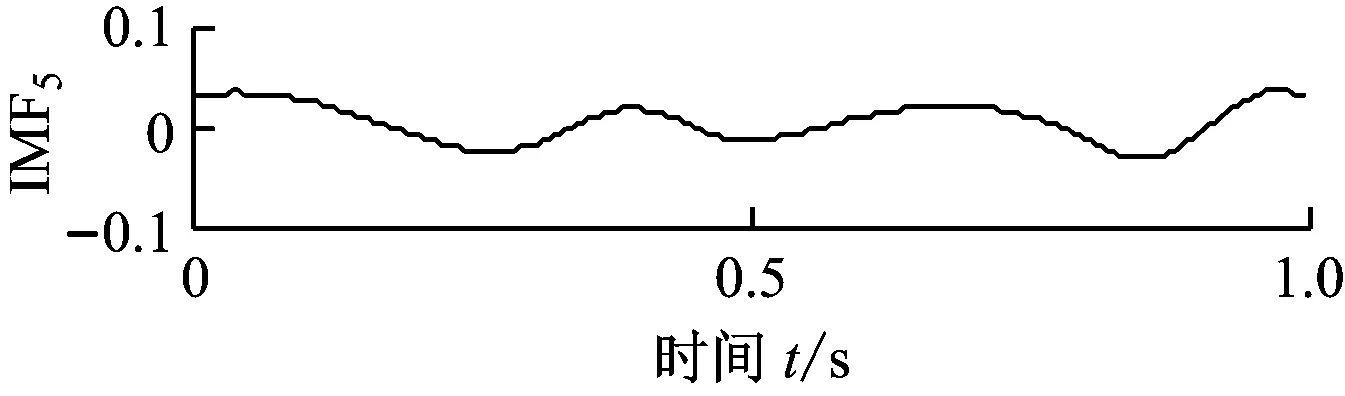

(b) x2(t)的EMD分解结果
图3 仿真信号的EMD分解结果
Fig.3 EMD decomposition results of simulated signals

图4 Bently RK4转子实验台Fig.4 Bently RK4 platform

图5 油膜涡动信号Fig.5 Oil whirl signal
5 结 论
结合自适应局部迭代滤波和希尔伯特变换,提出了基于ALIF-HT的汽轮发电机组转子故障诊断方法.ALIF通过Fokker-Planck方程实现了滤波函数的自适应选取,可有效提取出多分量非平稳信号的组成分量,避免了EMD存在的模态混叠问题.转子油膜失稳故障诊断实例表明,ALIF-HT方法能够成功地提取转子故障振动信号各谐波频率的时频信息,分析效果优于HHT方法,为转子故障诊断提供了一种新途径.

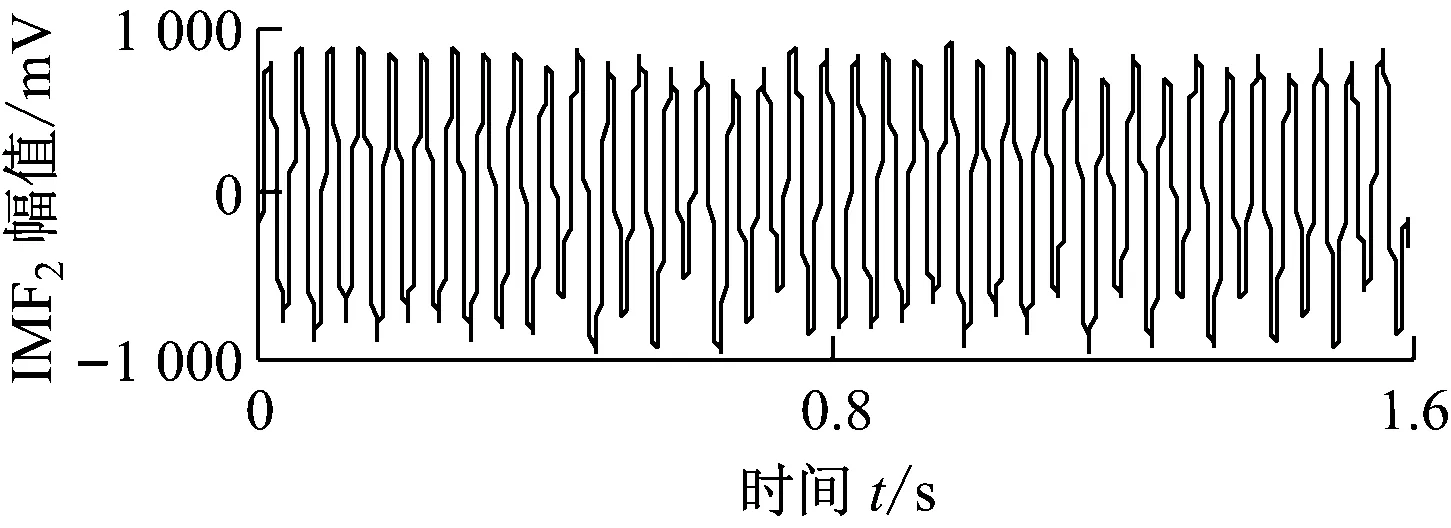
(a) 油膜涡动信号的ALIF分解结果
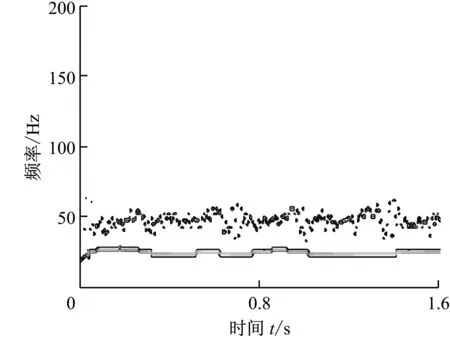
(b) 油膜涡动信号的ALIF-HT时频图图6 油膜涡动信号的ALIF-HT分析结果Fig.6 ALIF-HT analysis results of oil whirl signal






(a) 油膜涡动信号的EMD分解结果

(b) 油膜涡动信号的HHT时频图图7 油膜涡动信号的HHT分析结果Fig.7 HHT analysis results of oil whirl signal
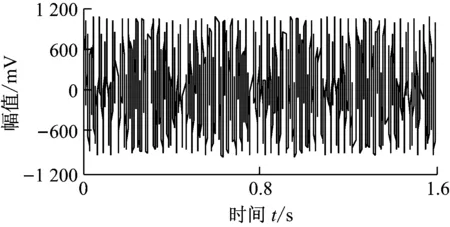
图8 油膜振荡信号Fig.8 Oil whip signal
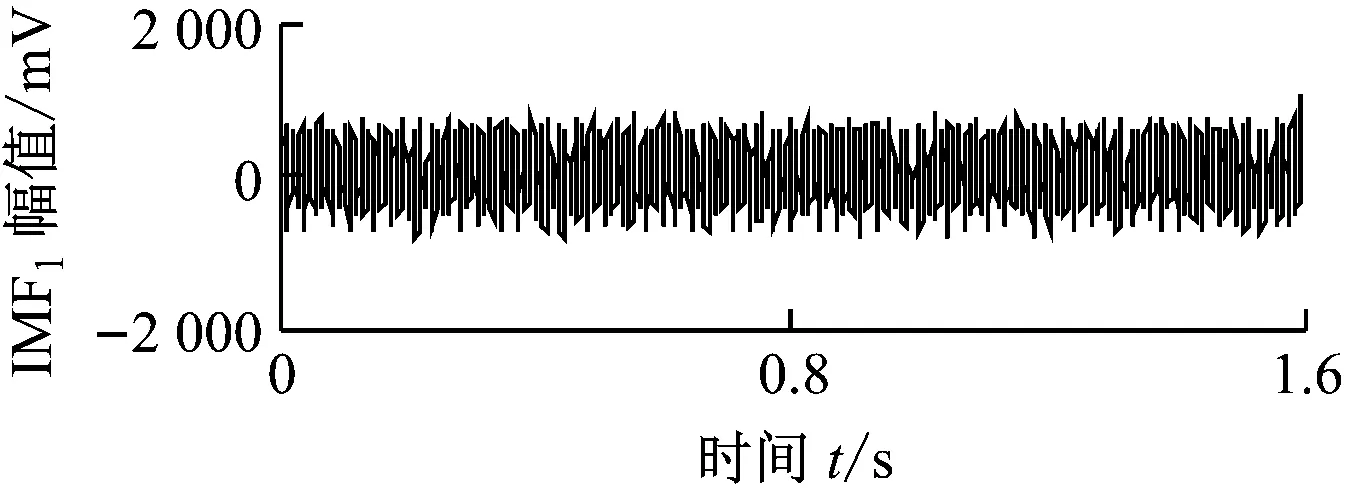
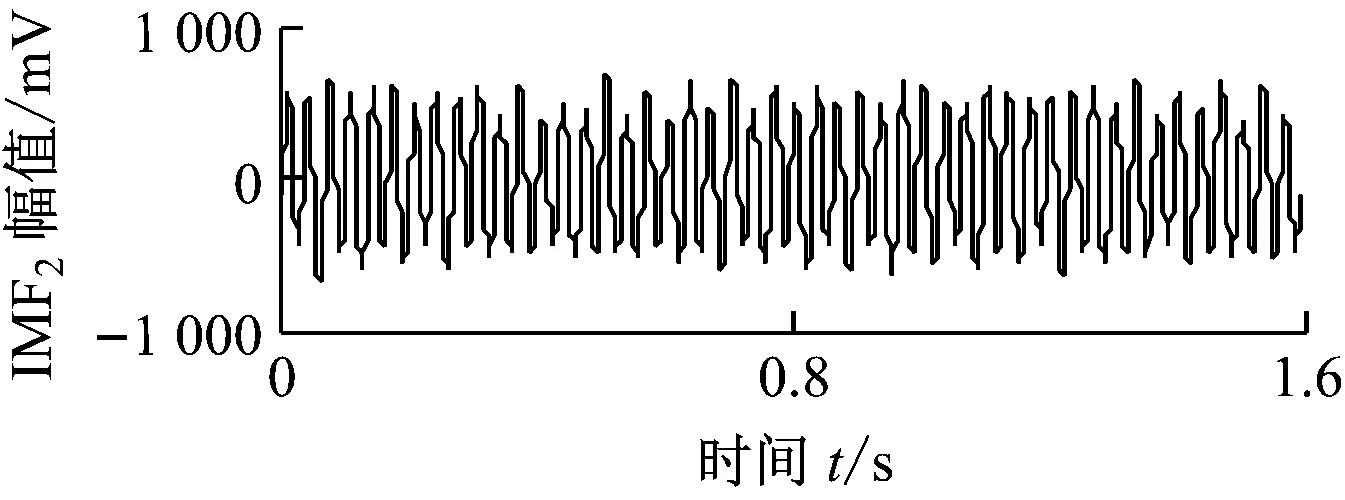
(a) 油膜振荡信号的ALIF分解结果
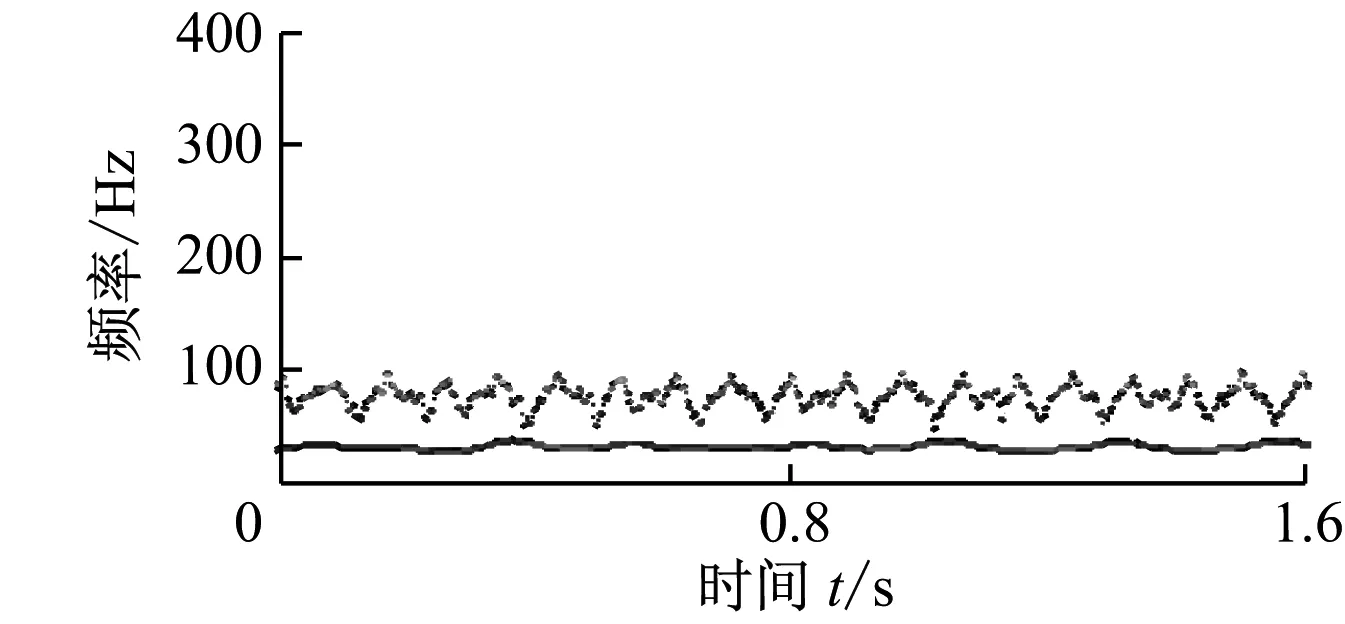
(b) 油膜振荡信号ALIF-HT时频图图9 油膜振荡信号的ALIF-HT分析结果Fig.9 ALIF-HT analysis results of oil whip signal

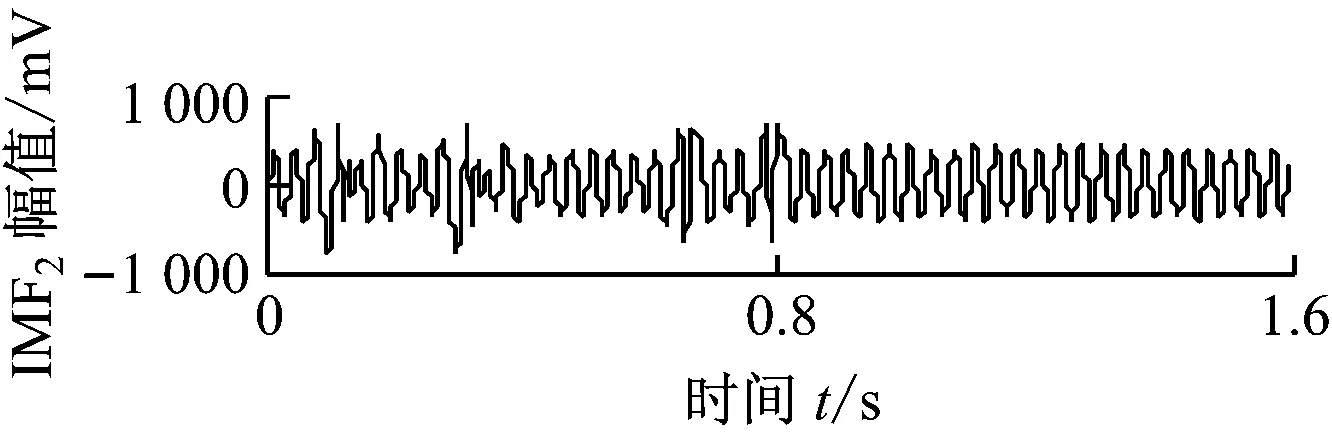
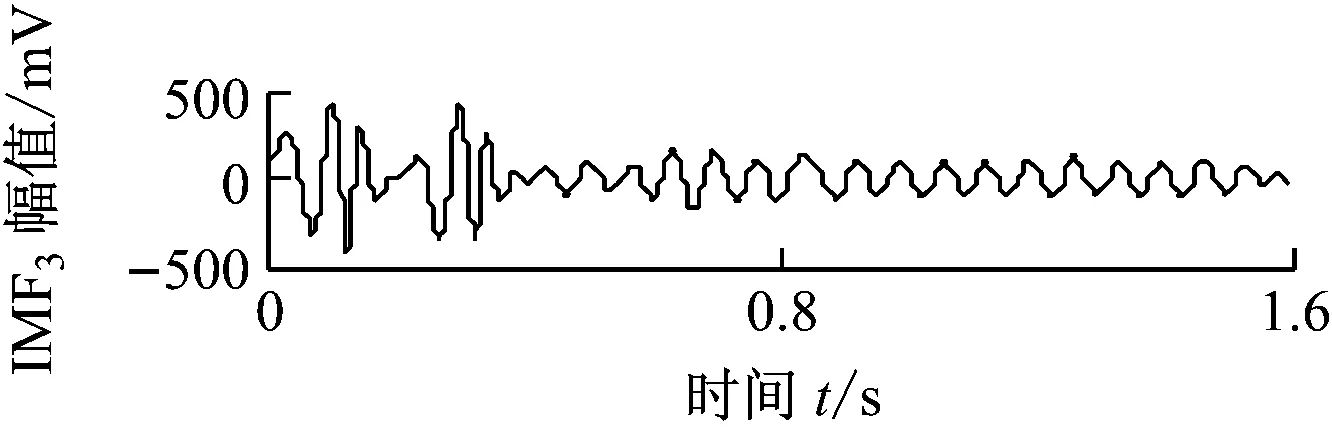


(a) 油膜振荡信号的EMD分解结果
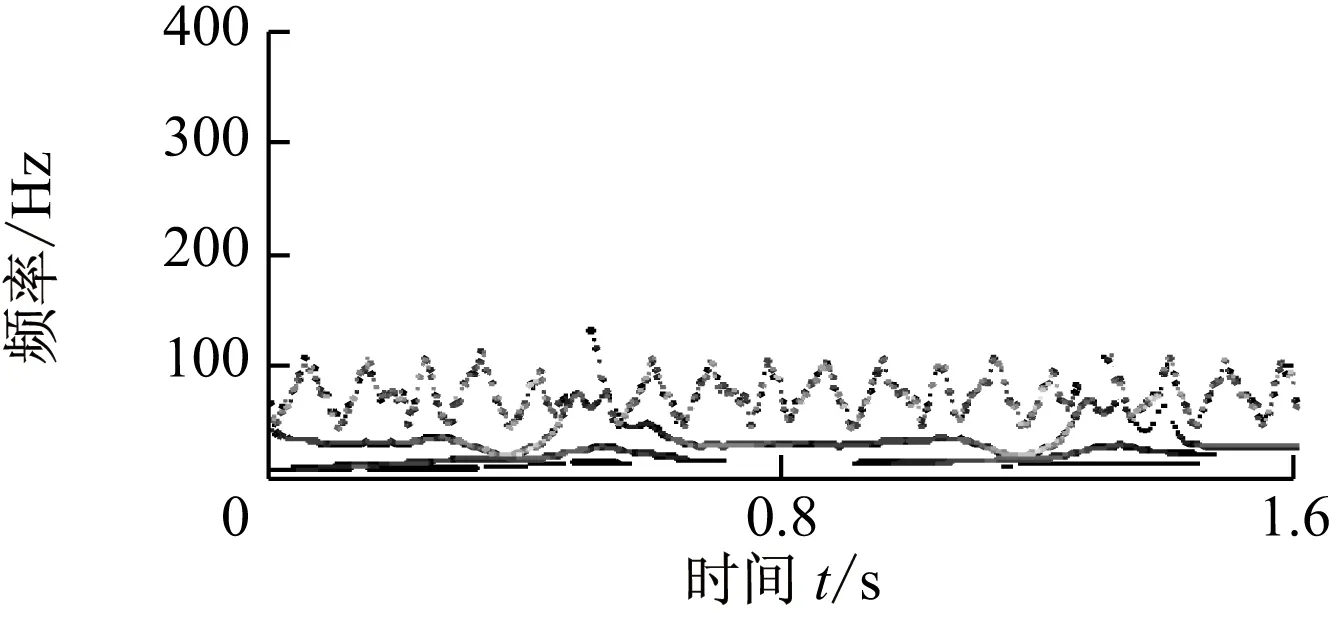
(b) 油膜振荡信号的HHT时频图图10 油膜振荡信号的HHT分析结果Fig.10 HHT analysis results of oil whip signal
[1] HU A J, HOU L L, XIANG L. Dynamic simulation and experimental study of an asymmetric double-disk rotor-bearing system with rub-impact and oil-film instability[J].NonlinearDynamics, 2016, 84(2): 641-659.
[2] 唐贵基, 向玲, 朱永利. 基于HHT的旋转机械油膜涡动和油膜振荡故障特征分析[J].中国电机工程学报, 2008, 28(2): 77-81.
TANG Guiji, XIANG Ling, ZHU Yongli. Analysis of oil whirl and oil whip based on Hilbert-Huang transform for rotor system[J].ProceedingsoftheCSEE, 2008, 28(2): 77-81.
[3] CHANDRA N H, SEKHAR A S. Fault detection in rotor bearing systems using time frequency techniques[J].MechanicalSystemandSignalProcessing, 2016, 72-73: 105-133.
[4] BALAZS P, BAYER D, JAILLET F, et al. The pole behavior of the phase derivative of the short time Fourier transform[J].AppliedandComputationalHarmonicAnalysis, 2016, 40(3): 610-621.
[5] YAN R Q, GAO R X, CHEN X F. Wavelets for fault diagnosis of rotary machines: a review with applications[J].SignalProcessing, 2014, 96: 1-15.
[6] 潘虹. 基于LMD和Wigner-Ville分布的水力机组振动信号分析[J].排灌机械工程学报, 2014, 32(3): 220-224.
PAN Hong. Analysis on vibration signal of hydropower unit based on local mean decomposition and Wigner-Ville decomposition[J].JournalofDrainageandIrrigationMachineryEngineering, 2014, 32(3): 220-224.
[7] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].ProceedingsoftheRoyalSocietyAMathematical,PhysicalandEngineeringSciences, 1998, 454: 903-995.
[8] 唐贵基, 庞彬. 基于改进希尔伯特振动分解的机械故障诊断方法研究[J].振动与冲击, 2015, 34(3): 167-171.
TANG Guiji, PANG Bin. Research for a mechanical fault diagnosis method based on improved Hilbert vibration decomposition[J].JournalofVibrationandShock, 2015, 34(3): 167-171.
[9] 武英杰, 刘长良, 范德功. 基于自适应高频谐波LMD法的风电机组故障诊断[J].动力工程学报, 2014, 34(12): 952-958.
WU Yingjie, LIU Changliang, FAN Degong. Wind turbine fault diagnosis based on adaptive high frequency harmonics LMD[J].JournalofChineseSocietyofPowerEngineering, 2014, 34(12): 952-958.
[10] 杨宇, 王欢欢, 程军圣. 基于ITD改进算法和关联维数的转子故障诊断方法[J].振动与冲击, 2012, 31(23): 67-70.
YANG Yu, WANG Huanhuan, CHENG Junsheng. A rotor fault diagnosis method based on ITD improved algorithm and correlation dimension[J].JournalofVibrationandShock, 2012, 31(23): 67-70.
[11] LEI Y G, HE Z J, ZI Y Y. Application of EEMD method to rotor fault diagnosis of rotating machinery[J].MechanicalSystemandSignalProcessing, 2009, 23(4): 1327-1338.
[12] 任大千, 杨世锡, 吴昭同, 等. LMD时频分析方法的端点效应在旋转机械故障诊断中的影响[J].中国机械工程, 2012, 23(8): 951-956.
REN Daqian, YANG Shixi, WU Zhaotong, et al. Research on end effect of LMD based time-frequency analysis in rotating machinery fault diagnosis[J].ChinaMechanicalEngineering, 2012, 23(8): 951-956.
[13] 郑近德, 程军圣, 聂永红, 等. 完备总体平均局部特征尺度分解及其在转子故障诊断中的应用[J].振动工程学报, 2014, 27(4): 637-646.
ZHENG Jinde, CHENG Junsheng, NIE Yonghong, et al. Complete ensemble local characteristic-scale decomposition and its application to rotor fault diagnosis[J].JournalofVibrationEngineering, 2014, 27(4): 637-646.
[14] LIN L, WANG Y, ZHOU H M. Iterative filtering as an alternative algorithm for empirical mode decomposition[J].AdvancesinAdaptiveAnalysis, 2009, 1(4): 543-560.
[15] CICONE A, LIU J F, ZHOU H M. Adaptive local iterative filtering for signal decomposition and instantaneous frequency analysis[J].AppliedandComputationalHarmonicAnalysis, 2016, 41(2): 384-411.
FaultDiagnosisofaTurbo-GeneratorRotorBasedonALIF-HT
TANGGuiji,PANGBin
(School of Energy, Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, Hebei Province, China)
Aiming at the problems that the vibration signals of turbo-generator rotor are of the multi-component and non-stationary kind, a new fault diagnosis method was proposed based on ALIF-HT by combining the novel signal decomposition method—adaptive local iterative filtering (ALIF) with the Hilbert transform (HT). The specific way is to decompose the original vibration signals of turbo-generator rotor into several signal components by ALIF, then to compute the instantaneous frequency of every component by HT to get the complete time-frequency representation of all signal components, and finally to identify the fault types according to the time-frequency characteristics. The ability of ALIF in decomposing multi-component signals was demonstrated through analysis on simulated signals and the engineering practicability of the method was verified via fault analysis of rotor oil film instability. Results show that the ALIF overcomes the mode-mixing problem existing in EMD and the ALIF-HT method has higher time-frequency accuracy than the HHT method.
turbo-generator; rotor; fault diagnosis; adaptive local iterative filtering; Hilbert transform
2016-12-06
国家自然科学基金资助项目(51307058);河北省自然科学基金资助项目(E2014502052);中央高校基本科研业务费专项基金资助项目(2017XS134)
唐贵基(1962-),男,山东黄县人,教授,博士,研究方向为机械状态监测与故障诊断.电话(Tel.):0312-7525028;
E-mail: tangguij@126.com.
1674-7607(2017)11-0883-07
TK288
A
470.30
