喷动流化床传热特性的CFD-DEM模拟
2017-11-28卜昌盛王昕晔张居兵朴桂林
卜昌盛, 王昕晔, 张居兵, 朴桂林
(南京师范大学 能源与机械工程学院, 江苏省能源系统过程转化与减排技术工程实验室, 南京 210042)
喷动流化床传热特性的CFD-DEM模拟
卜昌盛, 王昕晔, 张居兵, 朴桂林
(南京师范大学 能源与机械工程学院, 江苏省能源系统过程转化与减排技术工程实验室, 南京 210042)
基于颗粒-颗粒、颗粒-流体间的传热机制建立了颗粒尺度下的传热模型,并将其与计算流体力学-离散颗粒模型(CFD-DEM)耦合,建立了CFD-DEM传热模型,在传热计算中采用真实的颗粒接触刚度修正了颗粒-颗粒间的传热。采用典型喷动流化床内的颗粒传热实验数据验证了 CFD-DEM传热模型的准确性,并利用该模型分析了喷动流化床内的传热特性。结果表明:喷动流化床内颗粒的传热系数受其运动状态的影响,颗粒在环隙区域外循环的传热系数比内循环传热系数大;喷动流化床内平均传热系数呈对称分布,流化区域内的平均传热系数大于非流化区域,床体底部两侧及气体入口处的平均传热系数最大,床层中央区域的平均传热系数较小.
喷动流化床; 传热特性; 传热模型; CFD-DEM
流化床具有很高的传热和传质速率,被广泛应用于石油化工、能源、食品及药品加工等领域. 在这些领域的流化床工艺过程中,气固及固固间的传热特性对流化床内颗粒的物理化学过程至关重要. 深入揭示流化床内气固两相的传热规律和机理对流化床的设计、运行和控制具有重要意义.
近二十年来,针对稠密气固两相流的计算流体力学(CFD)数值模拟发展迅速,主要包括基于欧拉-欧拉框架的双流体模型(TFM)、基于欧拉-拉格朗日框架的离散颗粒模型(DEM)及直接模拟(DNS)[1]. 在研究稠密气固流动方面CFD已逐渐成熟,将气固传热机制与CFD耦合,研究和揭示气固体系内的传热特性,已成为当前的研究热点之一. DNS要求流体网格尺寸小于颗粒尺寸,从而直接求解流体的流动和传热控制方程[2],但该方法计算量巨大,且模拟的颗粒数量极少. TFM将颗粒相假设为类似于流体的连续相. Chang等[3]将颗粒相传热与TFM耦合,成功建立了流化床的气固流动和传热模型,但该方法难以在颗粒尺度上对气固传热特性进行细致描述.
Zhou等[4-8]将传热模型与CFD-DEM模型耦合建立了CFD-DEM传热模型,研究了颗粒尺度下的气固流动和传热特性. Li等[9]将颗粒-颗粒、颗粒-壁面、颗粒-流体传热模型与CFD-DEM模型耦合,研究了气力输送条件下输送管道不同位置处的壁面温度变化。Shimizu[10]将气固传热模型的计算结果与相应的解析解进行对比验证,并将该模型与CFD-DEM模型耦合,研究了流化床内颗粒与热气流间的传热规律。Hobbs[11]基于CFD-DEM传热模型,模拟了沥青颗粒在滚筒式干燥机中的传热过程.Zhou等[12]建立了颗粒尺度下的气固、固固传热模型,并将其与CFD-DEM模型耦合,研究了固定床及鼓泡流化床条件下的有效传热系数和单颗粒的传热特性,定量分析了流体-颗粒间传热、颗粒-颗粒间传热以及辐射传热在颗粒传热过程中的作用机制.Zhao等[13]采用CFD-DEM传热模型考查了流化床埋管周围的气固流动及传热特性,发现埋管周围的传热系数呈椭圆形分布,即埋管左右两侧的传热系数大于埋管上下两侧的传热系数. 上述研究进一步揭示了颗粒尺度下流化床内气固流动及传热的作用机制,同时为CFD-DEM传热模型与颗粒尺度化学反应模型的耦合提供了便利条件.
然而,上述研究中描述颗粒-颗粒间传热过程的模型相对简单,如未考虑颗粒周围气膜及颗粒粗糙表面传热、未考虑颗粒-颗粒间传热。但已有研究[14-15]显示,颗粒周围的气膜层及颗粒粗糙表面对颗粒间传热的影响不可忽略,尤其是在固定床条件下。此外,为选取合理的计算时间步长,在CFD-DEM模型中颗粒接触刚度的取值远小于真实值,从而扩大了颗粒碰撞变形量的预测值,产生较大的传热计算误差. 为此,笔者将颗粒-颗粒间传热和颗粒-流体间传热机制与CFD-DEM模型耦合,修正了模型中因颗粒接触刚度取值偏小而引起的传热计算误差,建立了改进的CFD-DEM传热模型.
将PTV(Particle Tracking Velocimetry)与红外热成像法相结合,可同时获得可视化流化床内颗粒的运动和温度等实验数据,已成为验证CFD-DEM传热模型的有效手段[16]. 笔者以Tsuji等[17]在尖晶石二维喷动流化床实验台上的传热实验数据为依据,验证了所建立的CFD-DEM传热模型的准确性,并基于该模型详细分析了喷动流化床内单颗粒的传热特性以及不同区域的传热特性.
1 CFD-DEM传热模型
在CFD-DEM模型中,气相用Navier-Stokes方程描述,采用DEM方法跟踪体系内的每个颗粒. 针对每个颗粒,考虑周围颗粒与其接触力、颗粒自身的重力以及气体对颗粒的曳力和压力梯度力. 气固两相间的作用力采用双向耦合,相间作用力满足牛顿第三定律. Liu等[18]已采用鼓泡流化床、埋管流化床和循环流化床的实验数据验证了冷态CFD-DEM模型预测气固流动特性的准确性. 在此基础上,笔者将冷态CFD-DEM模型与相间传热机制耦合(主要包括颗粒-颗粒直接导热、颗粒-流体-颗粒导热以及颗粒-气体对流传热),建立了CFD-DEM传热模型.
1.1颗粒相控制方程
DEM最早由Cundall等[19]提出,采用牛顿定律描述颗粒的运动、单颗粒的平动及转动,方程如下:
式中:mi为颗粒i的质量,kg;Vi为颗粒i的体积,m3;Fg、Fij,n、Fij,t和Fd分别为颗粒所受的重力、法向力、切向力以及颗粒与流体间作用力,N;pg为颗粒所在位置的压力梯度,Pa;vi和wi为颗粒i的线性速度矢量和角速度矢量;Ii为转动惯量,kg/m2;rj为颗粒j直径,m;K为颗粒接触刚度,N/m;η为颗粒碰撞切向恢复系数;θij,n和θij,t为颗粒间法向和切向变形量,m;nij和tij分别为颗粒i和颗粒j间法向单位向量和切向单位向量;N为单个流体网格内的颗粒数目;u为流体的速度矢量,m/s;μ为滑移摩擦因数;φf为流体体积分数,%;β为曳力系数.
1.2气相控制方程
气相控制方程主要包括连续性方程、动量方程及能量方程:
(6)
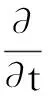
(7)
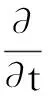
(8)
式中:ρf为流体密度,kg/m3;pf为流体压力,Pa;Vcell为单个流体网格的体积,m3;τf为剪切应力,N/m2;g为重力加速度,m/s2;Tf为流体温度,K;cpf为流体比热容,J/(kg·K);λf为流体热导率,W/(m·K);Qf,i为颗粒-流体间的传热量,W;Qf,wall为流体-壁面间的传热量,W.
1.3传热模型
单颗粒的能量控制方程为:
(9)
式中:Ti为颗粒i的温度,K;cpi为颗粒i的比热容,J/(kg·K-1);n为同时与颗粒i有热交换的颗粒数目;Qij,cond为颗粒-颗粒间的导热传热量,W;Qiwall,cond为颗粒-壁面间的导热传热量,W;Qi,conv为颗粒-流体间的对流传热量,W.
1.3.1 颗粒-颗粒间导热传热模型


图1 颗粒-颗粒直接接触导热示意图Fig.1 Particle-particle direct contact heat transfer

图2 颗粒-流体-颗粒导热示意图Fig.2 Particle-fluid-particle heat transfer
由图2可知,颗粒-流体-颗粒间的总传热热阻为:
Rt,pfp=Rsi+Rsg+Rsi
(10)
当颗粒-颗粒直接接触时,颗粒表面气膜受碰撞颗粒挤压后形成气隙,存在于颗粒接触面之间,如图1中的放大区域所示,此时Rsc、Rsg和Rsgg并联,颗粒-颗粒间的总传热热阻为:

(11)

表1 颗粒-颗粒传热中不同传热热阻的模型

传热模型中Rsi、Rsg和Rsgg的大小均与颗粒中心距Lij密切相关,而Lij的大小则由接触颗粒间的法向变形量θij,n直接决定. 直接接触颗粒-颗粒间的总传热热阻Rt,pp与θij,n的关系如图3所示,当θij,n从0增加到2.0×10-5mm时(CFD-DEM模型监测显示,接触颗粒间的θij,n在0~2.0×10-5mm内),Rt,pp急剧减小,因而获取准确的θij,n值对计算颗粒间的传热极为重要.
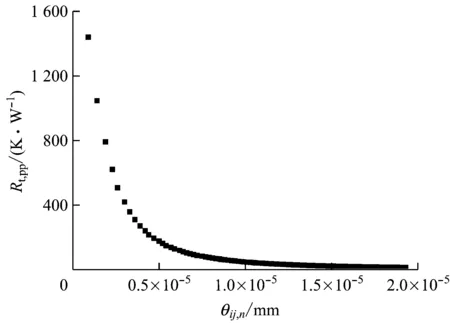
图3 颗粒-颗粒间总传热热阻与颗粒间法向变形量的关系
Fig.3 Total heat transfer resistance in particles vs. vertical deformation
DEM依据“软球模型”计算颗粒间的法向变形量θij,n,计算方程[19]如下:

(12)
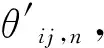
至此,颗粒-颗粒间的导热传热量为:
(16)
式中:Tj为颗粒j的温度,K.
颗粒-壁面间的传热采用类似的方法求解.
1.3.2 颗粒-流体间对流传热模型
颗粒雷诺数为:
Rei=ρfdiεi|uf-ui|/μf
(17)
式中:di为颗粒i的直径,m;εi为颗粒i所处网格的空隙率;uf为颗粒周围流体速度,m/s;ui为颗粒i的速度,m/s;μf为流体的动力黏度,Pa·s.
流化床内气固流动剧烈,Rei在空间、时间上发生大幅变化. 根据颗粒雷诺数的大小,颗粒-流体间的对流传热量采用下式计算:
Qi,conv=hi,convAi(Tf,i-Ti)
(18)
Nui=hi,convdi/λf
(19)
(20)
式中:Nu为努塞尔数;Pr为普朗特数;Ai为颗粒i的表面积,m2;Tf,i为颗粒i所处网格内流体的温度,K;hi,conv为颗粒i所处网格内颗粒与流体间的传热系数,W/(m2·K).
1.4边界条件和初始条件
初始条件:喷动流化床体壁面初始温度,T|wall,t=0=Two;颗粒初始温度,T|particle,t=0=Tpo,其中Two和Tpo分别为壁面和颗粒初始温度.
1.5颗粒传热系数的计算
颗粒传热系数是衡量气固传热特性的重要参数之一. 颗粒传热系数包括颗粒-流体间对流传热系数、颗粒-颗粒间导热传热系数和颗粒-壁面间导热传热系数. 传热系数(HTC)的计算方法见表2,其中hi,wall为颗粒i与碰撞壁面的导热传热系数,Twall为壁面温度.

表2 传热系数的计算方程
2 模型的数值求解
采用C语言编写三维DEM运动及传热程序,通过用户自定义接口编译进Fluent求解器,建立CFD-DEM数值传热模拟平台. 每个时间步长下,在计算流体流动前,DEM程序提供颗粒的速度、温度和位置等信息用于计算颗粒-颗粒间的传热量、流体网格内空隙率、颗粒与流体间相互作用力及热量交换等. 气固两相流场及温度场每隔0.025 s保存一次.
3 模型验证及结果分析
3.1模型验证
Tsuji等[17]采用PTV及红外热成像法对喷动流化床内颗粒的运动行为和温度变化进行了实验研究. 在实验中,喷动流化床床体的下半部为尖晶石,上半部为玻璃。初始温度为423 K的铝颗粒从一定高度自由下落,堆积于床体内,温度为292 K的空气从床体底部中央狭缝喷嘴进入,狭缝喷嘴尺寸为21 mm×11 mm,铝颗粒的最小临界流化风速为1.09 m/s,实验设定流化风速为1.5 m/s. 采用表3所示的实验数据[17]对所建立的CFD-DEM传热模型进行验证.
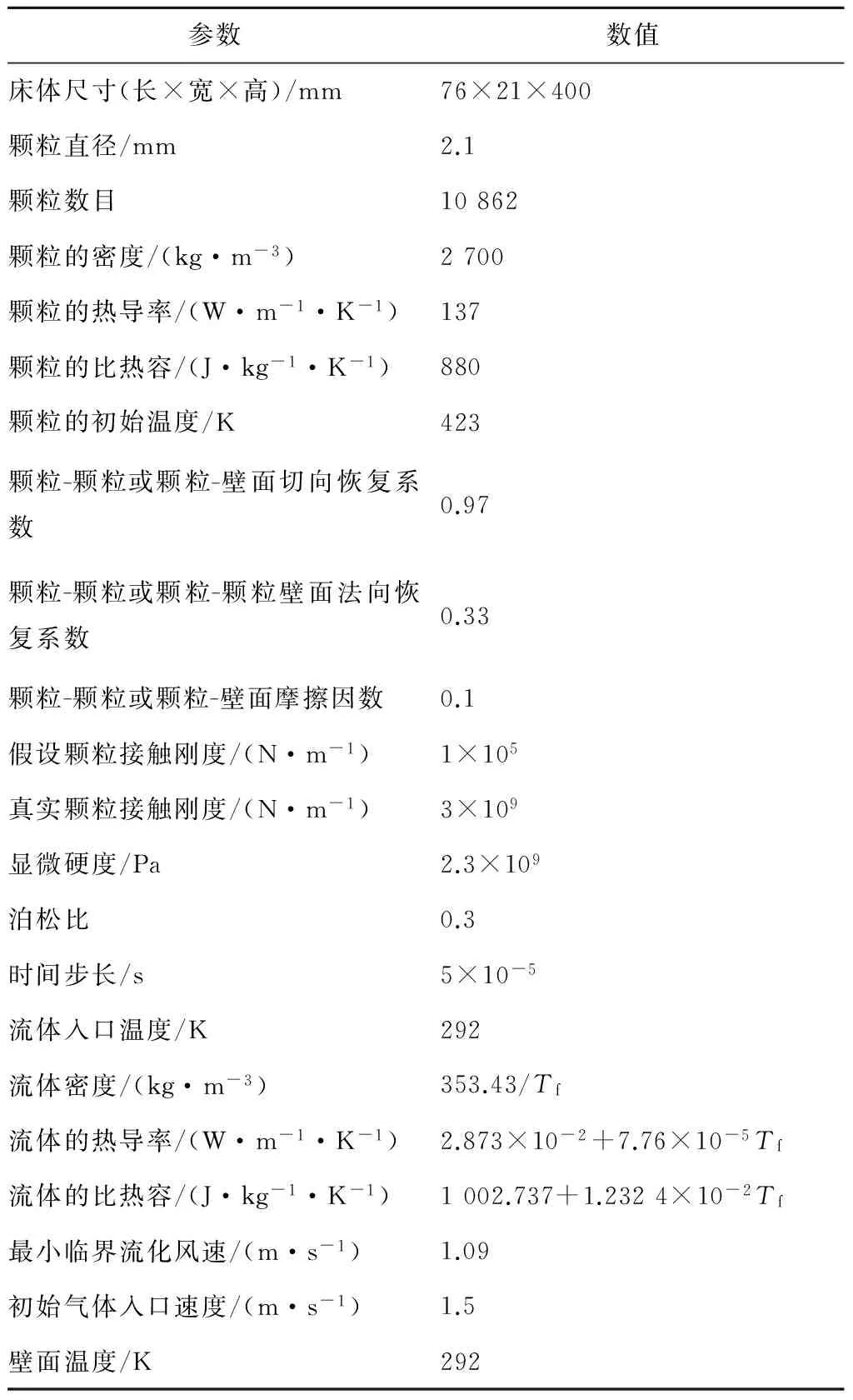
表3 数值计算选用的参数
根据CFD-DEM传热模型计算出颗粒温度,进而绘制出颗粒相的温度图,并与实验结果进行对比. 0.05~7.05 s内颗粒相温度随时间的变化如图4所示,图4(a)为实验结果,图4(b)为采用假设颗粒接触刚度计算所得的模拟结果,图4(c)为采用真实颗粒接触刚度计算所得的模拟结果. 由图4可以看出,在实验中,热颗粒加入喷动流化床后与周围环境进行传热,导致贴近壁面处的颗粒温度降低. 在模拟中,设置颗粒的初始温度为423 K. 对比图4(a)与图4(b)可知,图4(b)中颗粒温度降低的速度明显比实验中快,在7.05 s尤为显著. 这是因为模型在计算传热过程中选用的颗粒接触刚度远小于真实颗粒接触刚度,过大地预测了颗粒-颗粒间及颗粒-壁面间的碰撞法向变形量,大幅提高了颗粒-颗粒间及颗粒-壁面间的传热量,导致模型预测结果与实验结果存在较大差异. 当采用真实颗粒接触刚度修正颗粒间的碰撞传热量后,模拟结果与实验结果基本吻合,过量预测传热量的问题得到了有效解决.






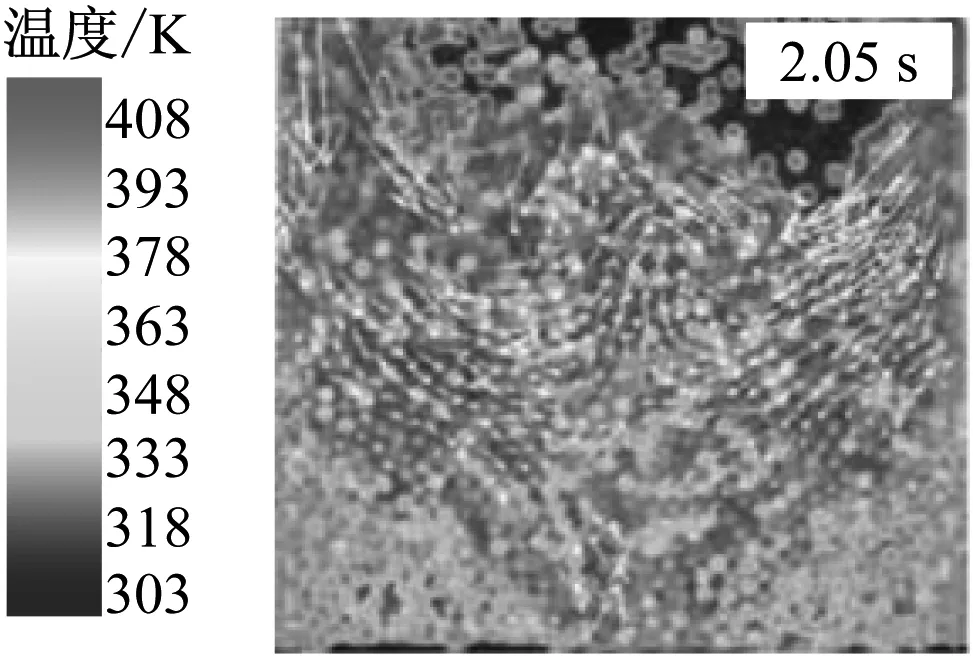





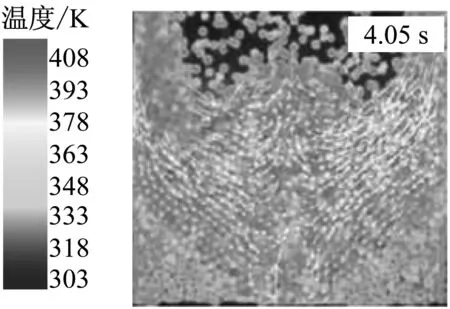









(a) 实验结果

(b) 假设颗粒接触刚度的模拟结果

(c) 真实颗粒接触刚度的模拟结果
图4 实验和模拟得到的不同时刻喷动流化床内颗粒的位置与温度
Fig.4 Experimental/simulated position and temperature of particles in a spouted fluidized bed at different moments
3.2颗粒的传热特性
3.2.1 单颗粒的传热特性
选取初始位置在床层中央的单颗粒作为研究对象,考察其位置、温度及传热系数随时间的变化规律.图5(a)给出了采用PTV测量所得不同初始位置颗粒的运动轨迹(其中数字代表不同的颗粒),图5(b)~图5(d)给出了模拟获得的0~7.05 s内每隔0.025 s颗粒的位置(即运动轨迹,其中X和Y为颗粒坐标位置)、温度及传热系数随时间的变化. 由图5(b)可以明显观察到颗粒参与了环隙区域的外循环(0~3.5 s)和内循环(3.5~7.05 s),与PTV的测量结果一致,表明CFD-DEM传热模型可准确预测喷动流化床内的气固流动. 在图5(c)中t1和t2时间段内,处于喷动流化床外循环下部的颗粒温度基本不变,但图5(d)显示的颗粒瞬时传热系数并不为零,主要原因在于该时间段内颗粒与周围环境的温差较小,传热量较小. 与此相应,图5(c)中部分时刻的颗粒温度迅速下降,且持续时间较长,此段时间内颗粒由床层底部经气流携带向上运动,气固间的相对速度大,对流传热较强,热量由热颗粒向冷空气快速传递. 由图5(d)可以看出, 0~3.5 s内颗粒的瞬时传热系数较3.5 s后大,表明喷动流化床内的颗粒在环隙区域的外循环传热系数比内循环传热系数大,因为参与环隙区域外循环的颗粒-颗粒、颗粒-流体的相对速度比内循环大,故而传热增强.
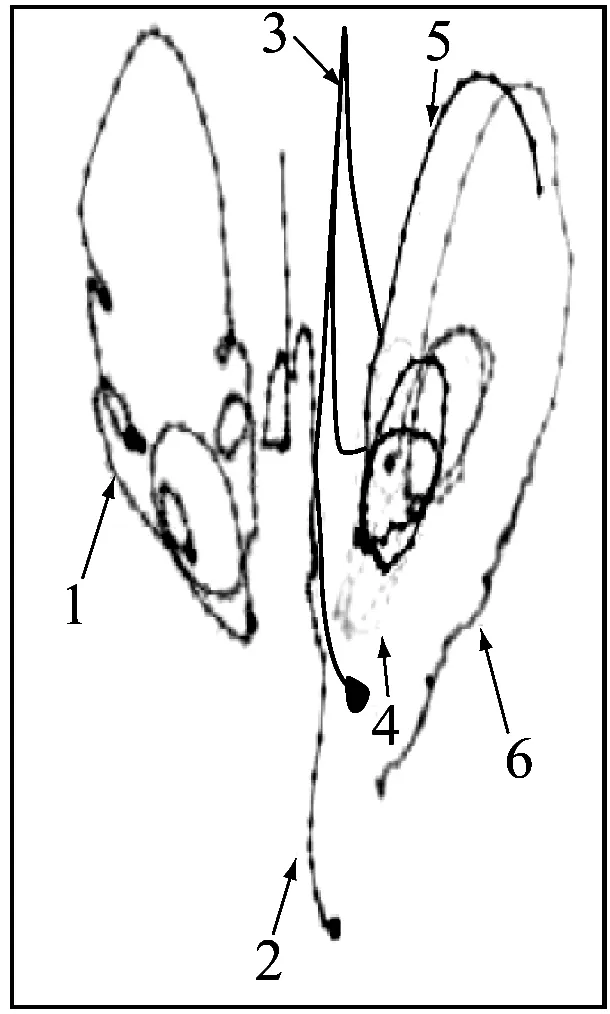
(a) 实验得到的颗粒运动轨迹

(b) 模拟得到的颗粒运动轨迹

(c) 温度随时间的变化

(d) 传热系数随时间的变化
图5 颗粒的运动轨迹以及颗粒温度和传热系数随时间的变化
Fig.5 Experimental/simulated trajectory of particles and variation of temperature and heat transfer coefficient with time
3.2.2 传热系数在喷动流化床内的分布特性
如图6所示,根据颗粒的运动状态可将喷动流化床内的流动区域分为流化区域和非流化区域,与非流化区域相比,流化区域内颗粒的运动更活跃,而且其温度更高.
选取2~7 s内气固流动及传热处于较稳定的状态,进一步分析喷动流化床内的传热特性. 喷动流化床内颗粒相在2~7 s时的平均传热系数见图7. 喷动流化床内左右两侧的平均传热系数呈对称分布,床体底部两侧非流化区域及喷动流化床气体入口处的平均传热系数较大,因此流化区域的平均传热系数显著小于非流化区域,这也解释了流化区域颗粒温度高于非流化区域的原因. 尽管非流化区域内的气流速度较低,但颗粒同时与喷动流化床侧面和前后面的壁面接触,导热接触面积较大,平均传热系数约为180 W/(m2·K);气体入口处的气固相对速度大,气固间的对流传热显著,平均传热系数约为150 W/(m2·K). 此外,床体上还存在平均传热系数相对较小的3个部分区域,分别位于喷动流化床中部的两侧及上部的中间区域,这3个区域内大部分颗粒同时向下或向上运动,颗粒-颗粒间及颗粒-流体间的相对速度较小,热导率较小,以对流传热为主.

图6 3.2 s时喷动流化床内的流动结构Fig.6 Flow structure in the spouted fluidized bed at 3.2 s

图7 2~7 s时喷动流化床内的平均传热系数分布
Fig.7 Average heat transfer coefficient in the spouted fluidized bed during 2-7 s
4 结 论
(1) 在传热模型耦合CFD-DEM模型中,采用真实颗粒接触刚度对颗粒碰撞传热过程进行了修正,计算所得的颗粒温度与实验结果吻合较好,所建模型为研究颗粒尺度下的气固流动及传热特性提供了参考。
(2) 喷动流化床内单颗粒的传热系数受其运动状态的影响,颗粒在环隙区域外循环的传热系数比内循环传热系数大;对喷动流化床整体而言,流化区域内的平均传热系数大于非流化区域,床体底部两侧及气体入口处的平均传热系数最大,床层中央区域的平均传热系数较小.
[1] DAN C, WACHS A. Direct numerical simulation of particulate flow with heat transfer[J].InternationalJournalofHeatandFluidFlow, 2010, 31(6): 1050-1057.
[2] YU Z S, SHAO X M, WACHS A. A fictitious domain method for particulate flows with heat transfer[J].JournalofComputationalPhysics, 2006, 217(2): 424-452.
[3] CHANG J, YANG S Q, ZHANG K. A particle-to-particle heat transfer model for dense gas-solid fluidized bed of binary mixture[J].ChemicalEngineeringResearchandDesign, 2011, 89(7): 894-903.
[4] ZHOU Z Y, YU A B, ZULLI P. A new computational method for studying heat transfer in fluid bed reactors[J].PowderTechnology, 2010, 197: 102-110.
[5] 武锦涛, 陈纪忠, 阳永荣. 移动床中颗粒接触传热的数学模型[J].化工学报, 2006, 57(4): 719-725.
WU Jintao,CHEN Jizhong,YANG Yongrong. Model of contact heat transfer in granular moving bed[J].CIESCJournal, 2006, 57(4): 719-725.
[6] 刘安源, 刘石. 流化床内颗粒碰撞传热的理论研究[J].中国电机工程学报, 2003, 23(3): 161-165.
LIU Anyuan, LIU Shi. Theoretical study on impact heat transfer between particles in fluidized bed[J].ProceedingsoftheCSEE, 2003, 23(3): 161-165.
[7] WAHYUDI H, CHU K W, YU A B. 3D particle-scale modeling of gas-solids flow and heat transfer in fluidized beds with an immersed tube[J].InternationalJournalofHeatandMassTransfer, 2016, 97: 521-537.
[8] HOU Q F, ZHOU Z Y, YU A B. Computational study of heat transfer in a bubbling fluidized bed with a horizontal tube[J].AIChEJournal, 2012, 58(5): 1422-1434.
[9] LI J, MASON D J. A computational investigation of transient heat transfer in pneumatic transport of granular particles[J].PowderTechnology, 2000, 112: 273-282.
[10] SHIMIZU Y.Three-dimensional simulation using fixed coarse-grid thermal-fluid scheme and conduction heat transfer scheme in distinct element method[J].PowderTechnology, 2006, 165(3): 140-152.
[11] HOBBS A. Simulation of an aggregate dryer using coupled CFD and DEM methods[J].InternationalJournalofComputationalFluidDynamics, 2009, 23(2): 199-207.
[12] ZHOU Z Y, YU A B, ZULLI P. Particle scale study of heat transfer in packed and bubbling fluidized beds[J].AIChEJournal, 2009, 55(4): 868-884.
[13] ZHAO Y Z, JIANG M Q, LIU Y L, et al. Particle-scale simulation of the flow and heat transfer behaviors in fluidized bed with immersed tube[J].AIChEJournal, 2009, 55(12): 3109-3124.
[14] TSORY T, BEN-JACOB N, BROSH T, et al. Thermal DEM-CFD modeling and simulation of heat transfer through packed bed[J].PowderTechnology, 2013, 244: 52-60.
[15] BU C S, LIU D L, CHEN X P, et al. Modeling and coupling particle scale heat transfer with DEM through heat transfer mechanisms[J].NumericalHeatTransfer,PartA:Applications, 2013, 64(1): 56-71.
[16] PATIL A V, PETERS E A J F, KUIPERS J A M. Comparison of CFD-DEM heat transfer simulations with infrared/visual measurements[J].ChemicalEngineeringJournal, 2015, 277: 388-401.
[17] TSUJI T, MIYAUCHI T, OH S, et al. Simultaneous measurement of particle motion and temperature in two-dimensional fluidized bed with heat transfer[J].KONAPowderandParticleJournal, 2010, 28: 167-179.
[18] LIU D Y, BU C S, CHEN X P. Development and test of CFD-DEM model for complex geometry: a coupling algorithm for Fluent and DEM[J].Computersamp;ChemicalEngineering, 2013, 58: 260-268.
[19] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J].Geotechnique, 1979, 29(1): 47-65.
[20] RONG D G, HORIO M. DEM simulation of char combustion in a fluidized bed[C]//SecondInternationalConferenceonCFDintheMineralsandProcessIndustriesCSIRO. Melbourne, Australia: [s.n.], 1999: 65-70.
CFD-DEMSimulationonHeatTransferCharacteristicsofaSpoutedFluidizedBed
BUChangsheng,WANGXinye,ZHANGJubing,PIAOGuilin
(Engineering Laboratory for Energy System Process Conversion amp; Emission Control Technology of Jiangsu Province, School of Energy and Mechanical Engineering, Nanjing Normal University, Nanjing 210042, China)
A CFD-DEM heat transfer model was established by coupling the model set up based on the mechanism of both particle-particle and particle-fluid-particle heat transfer with the computation fluid dynamics-discrete particle model (CFD-DEM), which adopts actual contact stiffness to calculate the heat transfer. The CFD-DEM heat transfer model was verified with experimental data of a typical spouted fluidized bed, and the model was then used to further study the heat transfer characteristics of the bed. Results indicate that the heat transfer coefficient of particles is greatly influenced by their flow status, and it is higher in interior cycle than in exterior cycle. The heat transfer coefficient is symmetrically distributed in the spouted fluidized bed, which is higher in fluidized region than in un-fluidized region. The highest heat transfer coefficient appears in both sides of the bed bottom and at the gas entrance, whereas, relatively low heat transfer coefficient exists in the middle region.
spouted fluidized bed; heat transfer characteristics; heat transfer model; CFD-DEM
2017-03-23
2017-04-17
国家自然科学基金青年基金资助项目(51606104);安徽省科技重大专项计划资助项目(15czz02045);江苏省高校自然科学研究面上资助项目(16KJB470010)
卜昌盛(1987-),男,江苏淮安人,讲师,博士,研究方向为气固流动模拟. 电话(Tel.):025-85481124;E-mail: csbu@njnu.edu.cn.
1674-7607(2017)11-0903-09
TK124
A
470.10
