水蒸气核化及单体生长过程的分子动力学研究

冯靖伊， 张燕平， 高 伟

(华中科技大学 能源与动力工程学院， 武汉 430074)

水蒸气核化及单体生长过程的分子动力学研究

冯靖伊， 张燕平， 高 伟

(华中科技大学 能源与动力工程学院， 武汉 430074)

通过分子技术模拟水蒸气凝结过程，采用非平衡分子动力学(NEMD)方法模拟并分析了凝结相变中核化及单体生长过程.计算相变过程中的凝结速率，并研究了核化和单体生长初期液态水的直径与凝结速率之间的关系，同时分析了模拟压力对凝结速率的影响.结果表明：在相同过冷度下，凝结速率随压力的降低而减慢；在核化及单体生长过程中，相同的压力和温度条件下，凝结相变的传热传质效果随着液体直径的增长而改善.

水蒸气； 分子动力学； 凝结速率； 液体尺寸； 传热传质

作为一种高效的传热方式，凝结换热一直是众多学者的重要研究方向.其中水蒸气的凝结换热更是被广泛应用于制冷[1]制热、发电和航空航天等工程生产实践中.几十年来无数学者对凝结换热进行了实验和理论研究[2-4]，但由于凝结相变本质的复杂性，目前对其机理研究尚不全面.

近年来，随着计算机性能的不断进步，分子模拟技术在传热传质方面的研究也迅速发展[5].Ikeshoji等[6]提出了适用于周期性边界条件的非平衡分子动力学算法来计算氩的导热系数，并通过该方法模拟氩蒸气的凝结相变过程，发现分子间能量和动能的传递分别在液相和气相的热量传递中起主要作用.Krasnochtchekov等[7]采用分子动力学方法模拟了气态纳米金属粒子的凝结相变过程，并在此基础上分析了表面偏析对金属粒子结构的影响.Nagayama等[8]用分子动力学(MD)方法模拟了直链烷烃分子(如丁烷、辛烷等)在气液界面上的凝结/蒸发行为，分析了相变的影响因素，并总结出凝结/蒸发系数的预测方法.Wang等[9]提出了修正过渡态理论，并采用分子动力学方法依据修正的过渡态理论模拟不同温度下氩蒸气的凝结系数.Desbiens等[10]研究了水蒸气在硅沸石材料中凝结吸附和液态水在疏水纳米孔洞中的不均匀流动过程.传热发生时传热物质形态和尺寸[11]的不同会导致换热效果差异较大，Diao等[12]通过构造冷源、热源以形成温度梯度，模拟分析对碳纳米管传热系数产生影响的因素，发现纳米管封口的存在会大大降低传热性能.而水蒸气凝结相变发生时传热物质形态也会影响相变效果，如膜状凝结的换热效率远低于珠状凝结，在珠状凝结实验数据[13]中也显示，水蒸气凝结时液体微团的尺寸对凝结效果也有影响，但是该宏观实验结果在微观方面并没有得到充分的模拟证实.

近年来针对凝结相变初期(核化及单体生长)的模拟也有一些研究，Mokshin等[14]通过使用粗粒度水分子模型模拟稳态均匀蒸气凝结的成核和单体生长过程.Diemand等[15]模拟了大规模的氩蒸气均匀成核现象,在证明模拟结果与实验值一致的基础上提出了新的基于自由能函数的经验成核模型.Zipoli等[16]提出了一种用于模拟水蒸气凝结核化的粗粒度模型，将粗粒度技术的适用范围扩展到成核现象,通过对比发现该模型在得到准确结果的前提下能够减少计算量.McGrath等[17]采用不同分子间相互作用势来模拟氩的核化过程，发现作用势之间临界核形成的自由能差异不能仅根据势的宏观性质差异来解释，并对经典成核理论的不准确进行了解释.

虽然已有研究者对凝结核化和单体生长过程进行了研究，但这些研究还不够充分，且对不同压力下凝结相变影响因素的分析也不够全面.笔者采用非平衡分子动力学(NEMD)方法，研究汽水换热过程中水蒸气在凝结过程中的核化及单体生长，模拟不同压力下水蒸气的凝结相变过程和传热传质现象，并研究了核化和单体生长过程中影响凝结换热效果的相关因素(如液滴尺寸)，为提高凝结换热效果提供参考.

1 模拟体系建立

采用分子模拟技术模拟汽水混合换热过程中水蒸气的凝结换热过程.模拟对象水分子选用CHARMM力场下的TIP3P[18]非刚体模型，水分子模型间的相互作用如下：

(1)

Uangle=Kangle(θ-θ0)2

(2)

Ubond=Kbond(r-r0)2

(3)

式(1)描述的是水分子间的作用势能，其中右侧第一项为长程静电作用项，第二项为短程L-J静电作用项.

整个体系初始状态为充满水分子的长方体模型，XYZ3个方向均采用周期性边界条件.整个模拟流程图见图1.

图1 模拟流程图Fig.1 Simulation flow chart

模拟过程分为2个阶段：第一阶段为预处理阶段，第二阶段为凝结相变阶段.第一阶段模型的初始状态为过热水蒸气.整个过程步长设为1 fs.为了节省计算时间采用势能截断方法对L-J势能进行处理，截断半径取1 nm.采用Ewald加和法(Ewald Sums)处理库仑力.分子初始速度按高斯分布取样,求解采用Verlet velocity算法.首先对模型进行能量最小化处理，使盒子中所有分子能量最小化；然后模拟退火处理，控制体系温度从470 K加热到520 K然后冷却至初始状态，处理总时间为200 ps.最后选用NVT系综模拟200 ps，过程中使用Nose-Hoover控温法将模拟温度控制为470 K，使模型体系达到稳态.在此基础上进行第二阶段的凝结相变模拟.

第二阶段采用非平衡态模拟方法.将模型中心置于点(0,0,0)处并按边长分为100等份，其中边长为L，每份长度为b，将立方体盒子的中心区域-6blt;xlt;6b，-6blt;ylt;6b部分设为冷源区域(符号C)，对该区域分子降温使水分子核化凝结.将x-1/2Lxgt;-15b，x+1/2Lxlt;15b，y-1/2Lygt;-15b，y+1/2Lylt;15b区域设为热源区域(符号H)，加热区域中的水分子，使该区域维持在过热蒸汽状态.中间区域(符号M)为传递热流区域并出现温度梯度，区域划分如图2所示.在非平衡过程中整个体系选用NVE系综，选用Langevin恒温器控制冷源温度在435 K,热源温度在475 K，模拟200万步共2.0 ns.

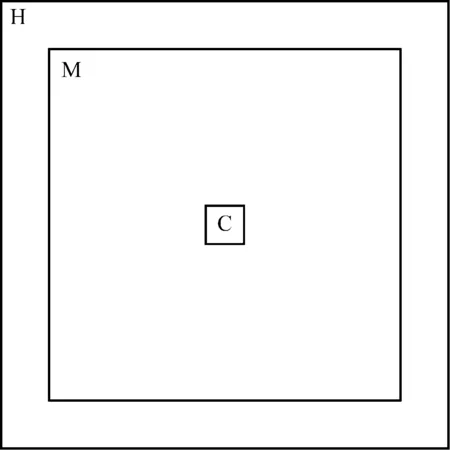
图2 冷源、热源及中间区域划分示意图Fig.2 Division of cold source, heat source and middle region

2 结果与讨论

2.1压力对凝结相变的影响

在0.4 ns的平衡态模拟后开始模拟凝结相变，图3给出了初始压力为1.7 MPa的模拟体系发生凝结相变的过程.非平衡态模拟进行到1.1 ns时，水分子相互聚集形成密度约为920 kg/m3的液滴，由成核阶段进入单体生长阶段，1.45 ns后液化速度减慢,分子数基本达到稳定.整个模拟过程中液相部分的形状有轻微变化，难以维持标准的球形.这是由液态水体积较小，气液界面波动的存在对液体形状影响较为明显造成的.

(a) 0.40 ns

(b) 0.55 ns

(c) 0.70 ns

(d) 0.85 ns

(f) 1.30 ns

(g) 1.45 ns

(h) 1.90 ns图3 水蒸气凝结相变过程Fig.3 Water vapor condensation process

通过模拟2.2 MPa、1.7 MPa和1.0 MPa 3个不同初始压力下水蒸气的凝结过程，并对发生凝结的水分子数目和模型压力进行记录，结果如图4和图5所示.3个不同初始压力的模型包含相同的原子数目、冷源过冷度和冷热源温差.图4为3个模型从非平衡态模拟开始到结束发生凝结相变的液相原子数随时间的增长情况.图5为各模型在非平衡态的压力变化示意图.从图5可以看出，相同条件下，压力降低，水蒸气的凝结速率也随之减慢.

图6给出了初始压力1.7 MPa,模型从非平衡态模拟开始，液态水的直径及直径增长速率随时间的变化情况.从图6可以看出，在液化过程开始到液滴直径达到稳定的过程中，液态水的直径增长速率呈现先增大后减小的趋势.模拟过程中，随着水蒸气凝结空间内的压力降低，直径增长速率应呈现减小的趋势，而0～0.6 ns时液态水的直径增长趋势与该规律并不相符，表明模拟过程中其他因素影响了凝结相变的速率.根据模拟结果，推测该影响因素为液滴尺寸：在核化和单体生长初期，随着凝结液相部分直径的增长速率加快.

图4 液相原子数变化Fig.4 Number of atoms in liquid phase

图5 模型压力变化Fig.5 Variation of simulation pressure

图6 核化及单体生长过程中液体直径的变化Fig.6 Variation of droplet size during nucleation and monomeric growth

2.2凝结相变的传热分析

以长12 nm、宽12 nm、高6 nm，初始压力1.7 MPa的模型为例，记录从非平衡态模拟阶段开始到结束的整个过程中冷源和热源的吸热量、放热量和模型内分子的能量状态.一方面通过冷源、热源的热流量累积可得到凝结相变过程中的换热量；另一方面通过记录模型中分子的动能、势能的变化情况也可以衡量凝结相变过程中的换热量.从相变开始到结束整个过程中累积的换热量如图7所示.

由图7可知，在0.5～0.8 ns内平均压力为0.921 MPa，该段时间内液化了的水分子数为30，总换热量为3 422.553 kJ/mol.图8给出了系统中分子总能量的变化.从图8可以看出，同样在0.5～0.8 ns气液界面的总能量的变化量(即总换热量)为3 018.293 kJ/mol.2种记录热流方法的总换热量值相差不大，证明了热流记录结果的合理性和准确性.

图7 换热量变化图Fig.7 Changes of heat exchange

图8 系统总能量变化Fig.8 Variation of total molecular energy in the system

为进一步分析模拟过程中的凝结换热效果，需计算单位时间内单位换热面积液滴的传热传质情况.通过记录各个时刻水分子的位置就可以得到各时刻水分子的空间分布以及在平面上的密度分布情况，从而得出液态水的位置及直径,并求得换热面积.在0.5～0.8 ns内，发生凝结的水分子数为30，经过计算可知该统计时段气液界面上平均凝结14.755个水分子/(nm2·ns)，释放潜热130.95 kJ/mol.整个模型内部各位置的温度可通过计算原子的动能得到，具体公式如下：

Ek=dim/2NkT

(4)

式中：Ek为原子总动能，J；dim为模拟的维度，取为3；N为原子个数；k为玻尔兹曼常数，取1.38×10-23J/K；T为温度，K.

根据记录和分析所得热流量总和Q、换热面积A和换热温差(通过统计温度分布可得)等条件，可以计算模拟过程中的平均凝结传热系数，0.5～0.8 ns内传热系数约为107W/(m2·K)，可以推测出在核化和单体生长初期阶段凝结相变的传热性能很好.

2.3尺寸对凝结速率的影响

由第2.1节分析得出，在凝结相变的核化和单体生长初期，随着凝结液态水直径的增长凝结换热效果越好.针对该推测构造边长分别为12 nm、18 nm和24 nm，高为6 nm的3个长方体模型.这3个模型具有相同的初始压力和温度分布；冷源、热源及中间区域的分布比例一致，且初始状态的分子密度相同，经过平衡态和非平衡态模拟使模型中心发生凝结相变形成液态水.模拟过程中监测体系的压力发生变化，在模型液态分子数趋于稳定前的0.3 ns，3个模型平均压力约为0.575 MPa，统计这0.3 ns内液相部分的平均换热面积，记录该时段水分子凝结数，得出3个模型的不同尺寸液体微团的水分子凝结速率，结果见表1.

表1 凝结速率与液体尺寸的关系

由表1可知，液体凝结速率随液体直径增长而加快.表明微观条件下凝结相变的核化及单体生长阶段凝结换热效果与液体的尺寸有关，并且凝结相变传热传质效果随液态水直径的增长而增强.Mokshin等[14]通过模拟不同温度下稳态均匀蒸气凝结，发现核化和单体生长过程中的液体微团直径大小与时间呈指数关系，王爱丽[13]关于滴状凝结的实验也得出在温度和压力不变的情况下凝结相变初期的凝结速率有一个快速增长时期，与本文非平衡态模拟的结果一致.

为进一步验证结论的正确性，针对3个模型在不同压力(0.678 MPa、0.575 MPa和0.472 MPa)下相同时长内的水分子凝结数进行统计，并换算成凝结相变释放的潜热量(见图9).由图9可知，相同压力下随着液滴直径的增长凝结相变传热传质效果更优.

表1和图9从不同的角度验证了“在凝结相变的核化和单体生长初期阶段，随着凝结液态水直径的增长凝结换热效果更好” 的推测(在不同压力下)的合理性，这是目前宏观实验和模拟中还没得到过的结果.

图9 不同压力下凝结释放的潜热量与液滴直径的关系Fig.9 Latent heat of condensation vs. droplet size at different pressures

3 结 论

(1) 相同过冷度条件下，随着压力的升高凝结速率越来越快，表明提高压力可以促进凝结相变的发生.

(2) 在凝结相变的核化和单体生长初期阶段，凝结相变的传热系数约为107W/(m2·K) ，表明凝结的这段过程具有良好的传热传质性能.

(3) 在凝结相变的核化和单体生长初期，随着液滴直径的增长凝结速率和凝结相变传热传质效果更好，这也是目前宏观实验和模拟还未观察到的结果.

[2] 胡申华, 严俊杰, 王进仕. 非等温表面Marangoni凝结特性的研究[J].动力工程学报, 2012, 32(1): 27-30.

HU Shenhua, YAN Junjie, WANG Jinshi. Study of Marangoni condensation characteristics on non-isothermal surface[J].JournalofChineseSocietyofPowerEngineering,2012, 32(1): 27-30.

[3] DAVIES J F, MILES R E H, HADDRELL A E, et al. Influence of organic films on the evaporation and condensation of water in aerosol[J].ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica, 2013, 110(22): 8807-8812.

[4] MILJKOVIC N, WANG E N. Condensation heat transfer on superhydrophobic surfaces[J].MRSBulletin, 2013, 38(5): 397-406.

[5] ACEVEDO O, JORGENSEN W L. Quantum and molecular mechanical Monte Carlo techniques for modeling condensed-phase reactions[J].WileyInterdisciplinaryReviews:ComputationalMolecularScience, 2014, 4(5): 422-435.

[6] IKESHOJI T, HAFSKJOLD B. Non-equilibrium molecular dynamics calculation of heat conduction in liquid and through liquid-gas interface[J].MolecularPhysics, 1994, 81(2): 251-261.

[7] KRASNOCHTCHEKOV P, ALBE K, AVERBACK R S. Simulations of the inert gas condensation processes[J].ZeitschriftfürMetallkunde, 2003, 94(10): 1098-1105.

[8] NAGAYAMA G, TAKEMATSU M, MIZUGUCHI H, et al. Molecular dynamics study on condensation/evaporation coefficients of chain molecules at liquid-vapor interface[J].TheJournalofChemicalPhysics, 2015, 143(1): 014706.

[9] WANG Z J, MIN C, GUO Z Y. Modified transition state theory for evaporation and condensation[J].ChinesePhysicsLetters, 2002, 19(4): 537-539.

[10] DESBIENS N, BOUTIN A, DEMACHY I. Water condensation in hydrophobic silicalite-1 zeolite: a molecular simulation study[J].TheJournalofPhysicalChemistryB, 2005, 109(50): 24071-24076.

[11] QI B J, WEI J J, ZHANG L, et al. A fractal dropwise condensation heat transfer model including the effects of contact angle and drop size distribution[J].InternationalJournalofHeatandMassTransfer, 2015, 83: 259-272.

[12] DIAO J K, SRIVASTAVA D, MENON M. Molecular dynamics simulations of carbon nanotube/silicon interfacial thermal conductance[J].TheJournalofChemicalPhysics, 2008, 128(16): 164708.

[13] 王爱丽. 滴状冷凝液滴微观特征及传热机制[D]. 大连: 大连理工大学, 2010.

[14] MOKSHIN A V, GALIMZYANOV B N. Steady-state homogeneous nucleation and growth of water droplets: extended numerical treatment[J].TheJournalofPhysicalChemistryB, 2012, 116(39): 11959-11967.

[15] DIEMAND J, ANGÉLIL R, TANAKA K K, et al. Large scale molecular dynamics simulations of homogeneous nucleation[J].TheJournalofChemicalPhysics, 2013, 139(7): 074309.

[16] ZIPOLI F, LAINO T, STOLZ S, et al. Improved coarse-grained model for molecular-dynamics simulations of water nucleation[J].TheJournalofChemicalPhysics, 2013, 139(9): 094501.

[17] McGRATH M J, GHOGOMU J N, TSONA N T, et al. Vapor-liquid nucleation of argon: exploration of various intermolecular potentials[J].TheJournalofChemicalPhysics, 2010, 133(8): 084106.

[18] MARK P, NILSSON L. Structure and dynamics of the TIP3P, SPC, and SPC/E water models at 298 K[J].TheJournalofPhysicalChemistryA, 2001, 105(43): 9954-9960.

MolecularDynamicsInvestigationonNucleationandMonomericGrowthofWaterVapor

FENGJingyi,ZHANGYanping,GAOWei

(School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

The process of water vapor condensation was simulated by molecular techniques, while the nucleation and monomeric growth of water vapor in phase change period were simulated and analyzed using non-equilibrium molecular dynamics (NEMD) method. A calculation was conducted on the steam condensation rate in the process of phase change, with a study on the effects of droplet size on the condensation rate in the initial period of nucleation and monomeric growth, and with an analysis on the influence of simulation pressure on the condensation performance. Results show that in the case of same degree of supercooling, the condensation rate decreases with the reduction of pressure. During the process of nucleation and monomeric growth, both the heat and mass transfer effectiveness are relatively good at the same pressure and temperature, which increase with the rise of droplet sizes.

water vapor; molecular dynamics; condensation rate; droplet size; heat and mass transfer

2016-11-07

2017-01-05

国家重点基础研究发展计划(973计划)资助项目(2015CB251504)

冯靖伊(1991-)，女，吉林长春人，硕士研究生，研究方向为分子动力学.

张燕平(通信作者)，女，副教授，博士，电话(Tel.)：15927592300；E-mail：zyp2817@hust.edu.cn.

1674-7607(2017)11-0912-06

TK124

A

470.10