引导小生境回溯优化算法

王 鹏，陈得宝，邹 锋，李 峥

淮北师范大学 物理与电子信息学院，安徽 淮北 235000

引导小生境回溯优化算法

王 鹏，陈得宝，邹 锋，李 峥

淮北师范大学 物理与电子信息学院，安徽 淮北 235000

回溯搜索优化算法（BSA）是近年提出的一种新型优化算法，针对其收敛速度较慢、易陷于局部最优的缺点，提出了一种基于最优个体引导和小生境技术相结合的改进BSA算法。本方法首先在BSA的变异操作中引入向最优个体学习的策略，以提高算法的收敛速度；其次，设计一种新的小生境排挤技术，根据每个个体到其他个体距离的平均最小值确定小生境半径，排除部分相似性较高的个体；结合群体当前的最差信息，设计一种新的变异方法产生一定数量的新个体补充到新的种群中，维持群体数量的恒定并增强群体多样性。改进的BSA算法充分考虑了算法的收敛速度和群体的多样性，较大地提高了传统BSA算法的性能。对10个典型函数进行仿真测试，并与其他算法结果进行对比，实验结果表明，改进算法在收敛速度与精度方面具有较好的效果。

回溯搜索优化算法；引导机制；小生境技术；变异策略

1 引言

群智能优化算法因其能解决一些传统优化方法难以求解的问题，广泛应用于函数优化、工程设计、自动控制等领域。常用的群智能算法有差分进化算法（DE）[1]、粒子群算法（PSO）[2]、蚁群算法（ACO）[3]、人工蜂群算（ABC）[4]等。为提高智能优化算法的性能，近些年来，研究者提出了一些改进型优化算法，如自适应差分进化算法（SADE）[5]，理解学习粒子群算法（CLPSO）[6]，快速全局优化的蚁群算法[7]，优秀种群引导的人工蜂群算法（GABC）[8]等，都不同程度地提高了智能优化算法的性能。

回溯搜索优化算法（BSA）是近年来提出的一种新型进化算法[9]。算法群体更新控制参数少，算法实现简单，在一些优化问题中发挥了重要的作用。与其他优化算法相比，BSA算法不仅运用当前的信息，而且运用历史信息对群体进行更新，充分利用了进化过程中不同时期的信息。目前对BSA算法的研究主要集中在两个方面，一方面是通过改进群体的产生办法提高算法的性能，这方面的研究工作目前取得的成果较少；另一方面是拓展BSA算法的应用领域。如利用BSA算法进行表面波分析并将其应用于天线设计[10]；BSA与DE算法结合解决无限制最优问题[11]；BSA与多种限制处理方法相结合，用于解决限制性最优问题[12]；对抗回溯算法（OBSA）应用于优化超混沌系统参数优化问题[13]等。

尽管BSA已成功应用于很多领域，但至少存在两方面的不足。首先，在BSA算法新个体产生的过程中，仅依赖于随机交叉和变异产生新个体，个体进化缺乏学习能力，群体的优化方向缺乏较好个体的引导，算法的收敛速度较慢；其次，随着进化过程的不断进行，与很多的其他进化算法一样，群体多样性丢失，导致个体趋于齐次，其历史信息和当前信息将会不变，导致个体不能更新自己的位置，算法将陷入局部最优。因此，研究如何提高BSA算法收敛速度的同时提高种群的多样性，对提高算法的整体性能十分重要。基于这样的分析，本文从提高BSA算法的收敛速度和精度两方面入手，通过引入学习机制和小生境技术提高算法的整体性能。本文算法的主要贡献有两个方面。一是通过在产生新个体的全过程中引入向最优个体学习，克服了原始BSA算法映射矩阵Map的某些位为零时相应位不更新的弱点，从而通过学习提高算法的收敛速度；二是由于算法收敛速度的加快，导致群体多样性快速丢失，本文方法设计一种新的小生境排挤方法，结合当前的最差个体信息，通过变异产生部分新个体，以弥补多样性丢失可能带来的早熟收敛问题。仿真实验表明改进算法能够有效地提高优化性能，在收敛速度和精度两个方面对原始算法有较大的提高。

2BSA算法

BSA算法是一种基于种群迭代的进化算法。基本BSA算法包含五个步骤，分别为：初始化，选择Ⅰ，变异，交叉，选择Ⅱ。基本框架如图1所示。其五个步骤简介如下。

图1 基本BSA框架

2.1 种群初始化

随机初始化种群P和历史种群oldP，如式（1）、（2）所示：

式中，i=1,2,3,…,N,j=1,2,3,…,D，N 为种群的规模，D为变量维数；U(·)是随机均匀分布函数；lowj与upj分别为变量的下界和上界；P为进化种群，oldP为历史种群。

2.2 选择Ⅰ

在每次迭代开始前，BSA首先产生一个新的历史种群oldP，如式（3）所示，进而对其进行随机排序，如式（4）所示：

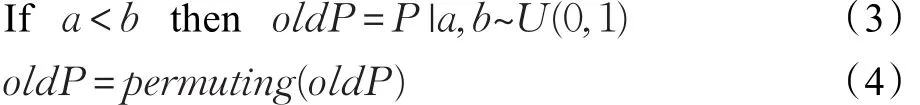
式中，a，b是服从（0，1）均匀分布的随机数，permuting(·)是随机排序函数。

2.3 变异

BSA算法采用变异策略如式（5）所示：

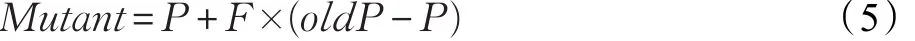
式中，F=3×randn，是变异尺度系数，能够控制个体变异的幅度，randn是标准正态分布随机数。

2.4 交叉

BSA的交叉过程分两步。首先定义一个大小为N×D的映射矩阵Map，其初始元素值均为零。然后用两种方式随机更新映射矩阵Map，如式（6）所示：

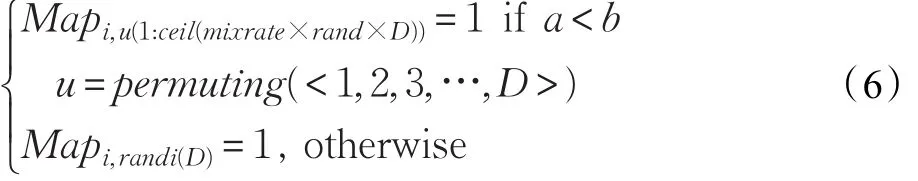
式中，mixrate是交叉率，本文中取值为1，ceil(·)为正方向取整函数，a和b均为均值为零方差为1的随机数，randi(·)是产生均匀分布随机整数函数，BSA根据生成的矩阵Map随机更新个体的某些位（具体操作如式（7）所示），并对新种群个体元素进行边界判断，若newP中的某位越界，则按照式（1）重新产生新位置。

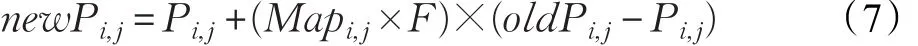
2.5 选择Ⅱ

根据个体适应度决定保留或更新个体，如式（8）所示：

式中，fitness(Pi)和 fitness(newPi)分别为个体 Pi更新前后的适应度值。

3 改进的BSA算法（GNBSA）

由式（7）可看出，新个体的产生由当代个体和历史个体确定，当群体多样性较差时，个体趋于齐次，导致个体不能更新，使算法陷入局部最优。此外，BSA算法中个体更新过程缺乏最优个体引导，算法缺乏学习能力。本文通过加入最优个体引导和小生境技术提高算法的整体性能。两个主要改进部分描述如下。

3.1 最优解引导机制

GNBSA算法在个体更新过程中引入当前代最优个体，为个体更新提供学习目标。由式（6）知，Map的初始值为0，假设被优化问题的维数为D，群体大小为N，则初始的映射矩阵如式（9）所示：

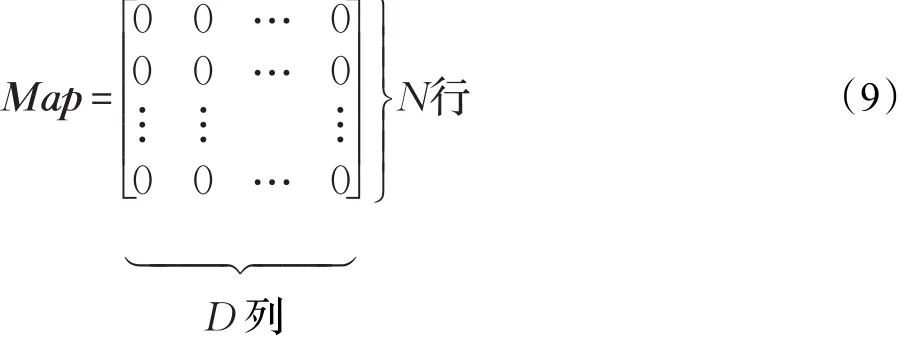
按照式（6）的方法，随机产生两个随机数a，b，若a＜b，对第i个个体，则u为一个元素维数标识打乱的1×D的向量，若 D=6 ，则 u=[2,3,5,4,6,1]，若 ceil（mixrate×rand×D）=3，则 Map 矩阵的第 i行2，3，5列元素为1，其他元素为0，如式（10）所示：

若a≥b，则在Map矩阵的第i行中任意选择一列为1，其他元素为0，例如任意选择到的列为3，则：新个体的产生方法如式（12）所示：

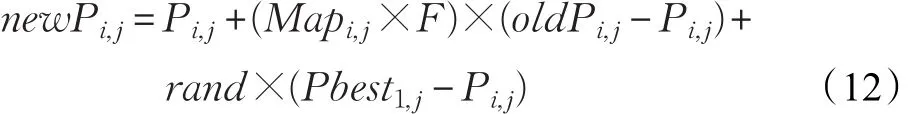
式中，Pbest为当前代全局最优个体的位置，rand是服从（0，1）均匀分布的随机数。由上述方法可知，对第i个个体，当Mapi,j=1时，第 j维变量的新值由个体的历史信息、当前信息及当前群体的最好位置确定。当Mapi,j=0时，新个体由最优个体引导产生。如式（13）所示：

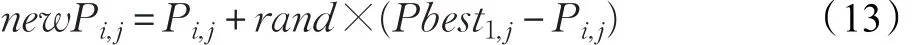
而传统的BSA方法中，当Mapi,j=0时，个体的该位将不发生变化。综上所述，在改进的BSA算法中，个体的每一维都向当前个体学习，不论映射矩阵相应位为0还是1，正是这样的操作，引导当前个体进行搜索，提高了算法的收敛速度。

3.2 排挤小生境技术

实践证明，算法收敛速度的加快有可能导致种群多样性丢失较快，从而加剧了局部收敛现象的产生。为均衡算法收敛速度和群体多样性，本文采用排挤小生境技术[14]改善种群多样性。为有效增加种群多样性，本文在分析小生境方法的基础上，设计了一种新的基于罚函数和结合最差个体信息的新个体产生排挤小生境方法。具体描述如下。

首先计算出种群中每个个体与其他个体间的欧氏距离d，如式（14）所示，然后计算出种群中每一个个体到其他任一个个体间欧式距离的最小值，得到一个最小值向量T，然后根据种群规模大小求其平均值得到小生境半径L，如式（15）所示。若d＜L，则比较两者的适应度，并对其中适应度较差的个体处以惩罚，使其适应度降低，如式（16）所示。

式（14）中，dkl是个体k与个体l之间的欧氏距离，j=1,2,3,…,D。式（16）中，fitness(Pk)是第k个个体的适应度，fitness(Pl)是第l个个体的适应度，Penalty为惩罚函数。

所有个体经过惩罚操作后，再按照适应度进行排序，适应度较差的m%×N个个体将被淘汰。为维持种群数量恒定，增加种群多样性，选取排在前面的m%×N个个体采用新的变异方式补充淘汰的个体，生成新的种群，m值的选取根据实际情况，采用经验方法确定。具体操作如下。

按照适应度值，求取当前种群中适应度最差的个体Pworst，按式（17）由排在前面的m%×N个个体和最差的个体变异产生新个体，并补充到新种群中。

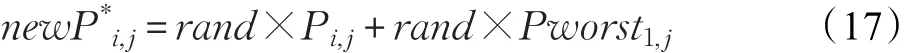
式中，i=1,2,3,…,m%×N,j=1,2,3,…,D，Pworst为当前种群最差个体的位置，newP*i,j为变异补充的个体。

通过这样的操作，在半径L之内只保留一个优秀个体，使得算法在保留较优解的同时，又维护了种群的多样性。

由于GNBSA算法的基本框架与BSA算法类似，所有个体同样经历选择Ⅰ，变异，交叉，选择Ⅱ，在GNBSA算法中，当种群经历选择Ⅱ的操作后，启动以上设计的小生境淘汰运算，各个体在自己的小生境半径内排除近似个体，并通过变异产生新个体，形成下一代种群。在算法流程中更加清晰地显示了小生境方法的作用位置。

3.3 改进算法流程

综合以上分析，GNBSA流程图如图2所示。

图2GNBSA算法流程图

4 仿真实验

4.1 实验参数设置

为验证GNBSA算法的有效性，选取10个典型函数优化问题对算法进行测试。同时利用BSA、PSOFDR[15]、PSOwFIPS[16]、JDE[17]四种算法对典型函数进行仿真实验，比较不同算法的性能。测试函数中，F1～F5是单峰函数，F6，F7为多峰函数，F8～F10为旋转函数。采用Matlab R2012b作为仿真软件，运行环境为Intel®Core™2 DuoE7400处理器，2 GB内存。测试函数如表1所示。各种算法的训练参数如下：种群规模为50，以函数值作为算法适应度，函数被评估次数（FES=5 000×D=150 000）作为算法的停止条件。在BSA和GNBSA中，交叉率 mixrate为 1，m=10。在 PSOFDR 中，wmin=0.4，wmax=0.9，φ1=1，φ2=1，φ3=2。 在 PSOwFIPS 中 ，w=0.729 8。在JDE中，F=0.5，CR=0.9。

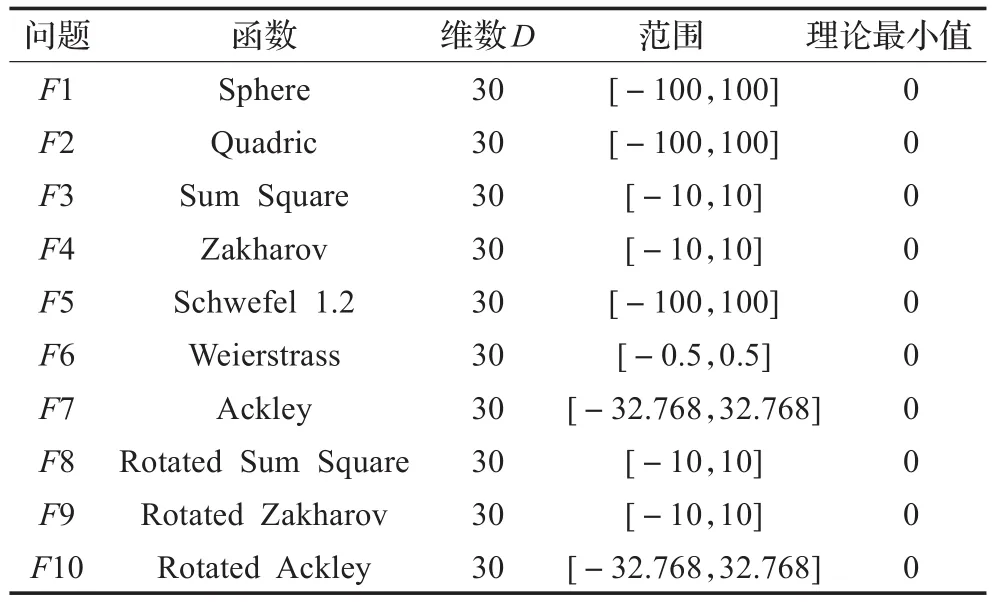
表1 测试函数

4.2 实验结果及分析

为公平比较，对同一函数，每种算法独立运行30次，对其统计特性进行比较。实验所得各种算法的平均值（mean）、方差（std）和最优值（best）如表2所示。从结果可以看出，与BSA相比，对所有测试函数，GNBSA算法的收敛精度和稳定性两方面均明显优于BSA，特别对于多峰函数F6 和F7 ，都能够找到理论最优解。对于单峰函数和旋转函数，平均收敛精度最少提高了6 个数量级，最多提高了116个数量级。与其他算法相比，GNBSA同样有着较好的性能，其收敛的平均解和方差均最小。

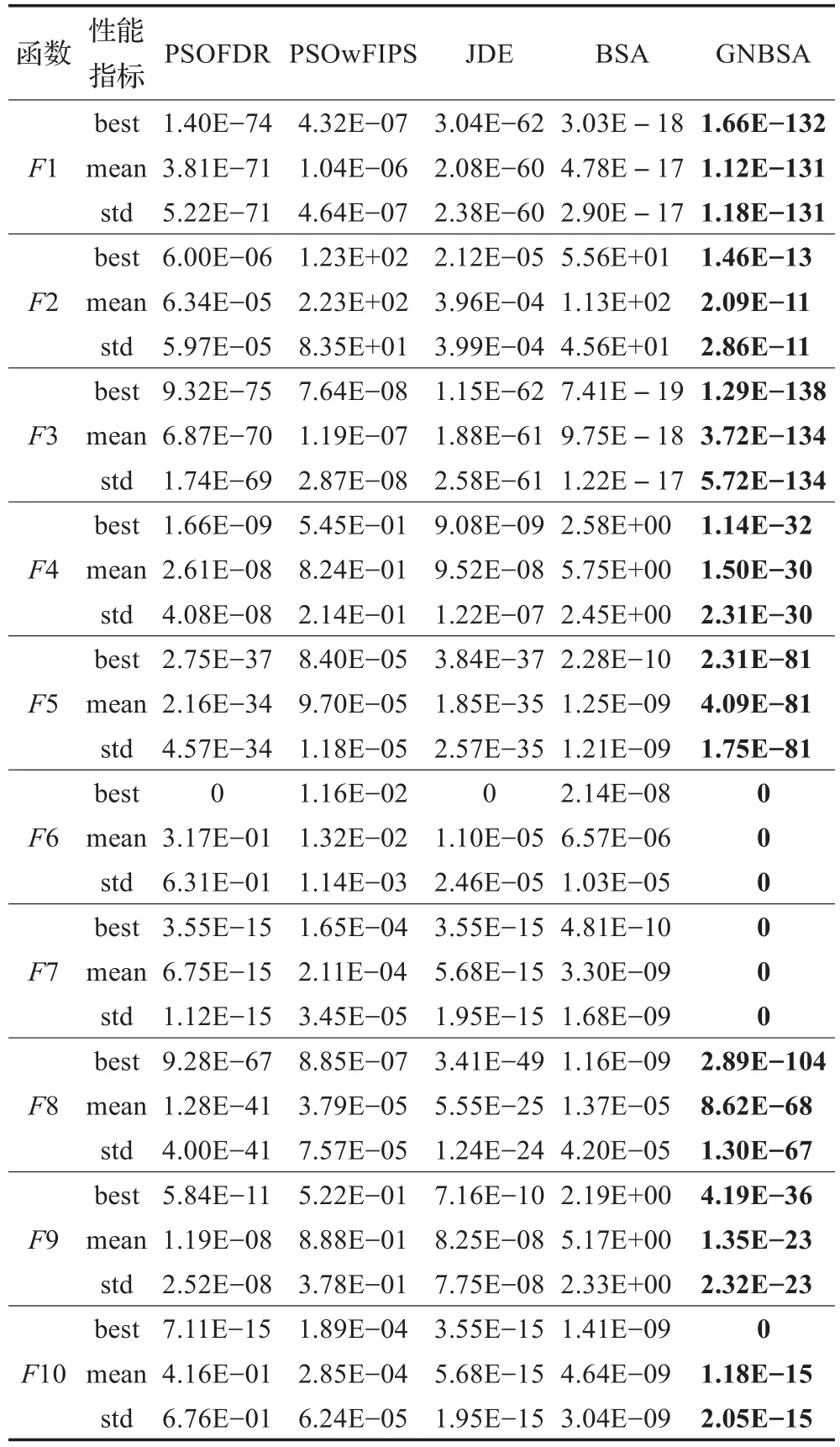
表2 5种算法对10个函数的测试结果

为显示改进算法的收敛速度，不同算法的在不同FEs 时的平均最优适应度变化如图3 所示。从图3 可看出，与其他算法相比，GNBSA 算法的收敛速度普遍较快。对函数F1 到F8 ，收敛速度明显快于其他四种算法。对函数F9 ，在初始阶段，GNBSA算法的收敛速度优势不明显，但在后期较快。对函数F10 ，GNBSA 算法的收敛速度与JDE 算法相当。图3 显示，GNBSA 算法相对于标准的BSA算法速度明显提高。

为进一步检测GNBSA算法的解与其他算法解的优劣，采用双边t-test 方法对结果进行检验，显著水平为0.05。GNBSA 算法对其他算法的t 值和p 值如表3 所示。表3 中，‘B’，‘W’，‘S’分别表示GNBSA算法性能优于、劣于、等于其他算法的数量。从表3 可看出，在显著水平为0.05 的情况下，GNBSA算法性能优于其他算法，解可以被接受。

在GNBSA算法中，小生境操作中，删除和补充个体的数量对算法性能具有一定的影响，删除太多，群体信息丢失太多，不利于算法对原有信息的利用，删除太少，群体多样性难以维持，为分析参数m 对算法性能的影响，本文选取三个函数(F1,F5,F8) 对其影响进行分析，结果如表4 所示。从表4 中可以看出，m 的取值对算法性能具有一定的影响，刚开始m 值的增大，优化性能得到一定的提升，当m 增加到一定值之后，再增加m 的值，群体信息丢失增加，算法性能反而下降，本文经验选择m 的值为10，对这几个函数效果较好。

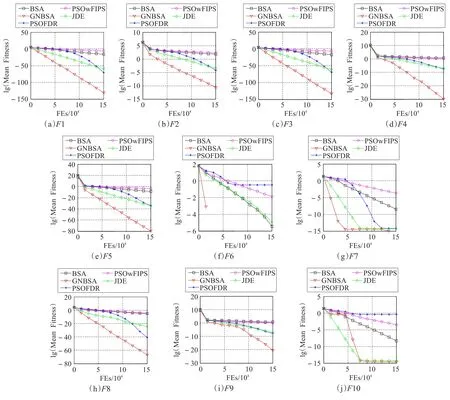
图3 10 个函数的平均最好适应度变化图

5 结束语

本文提出了一种基于引导和小生境技术的BSA改进算法（Gbest-guided and Niching Backtracking Search Optimization Algorithm）。相对于标准的BSA算法，GNBSA算法在个体的更新过程中加入了全局最优解的引导。引入排挤机制的小生境方法来维持种群多样性。通过对典型函数的优化测试验证了方法的有效性。从比较结果可看出，无论在收敛速度和收敛精度方面，改进算法具有较好的性能。

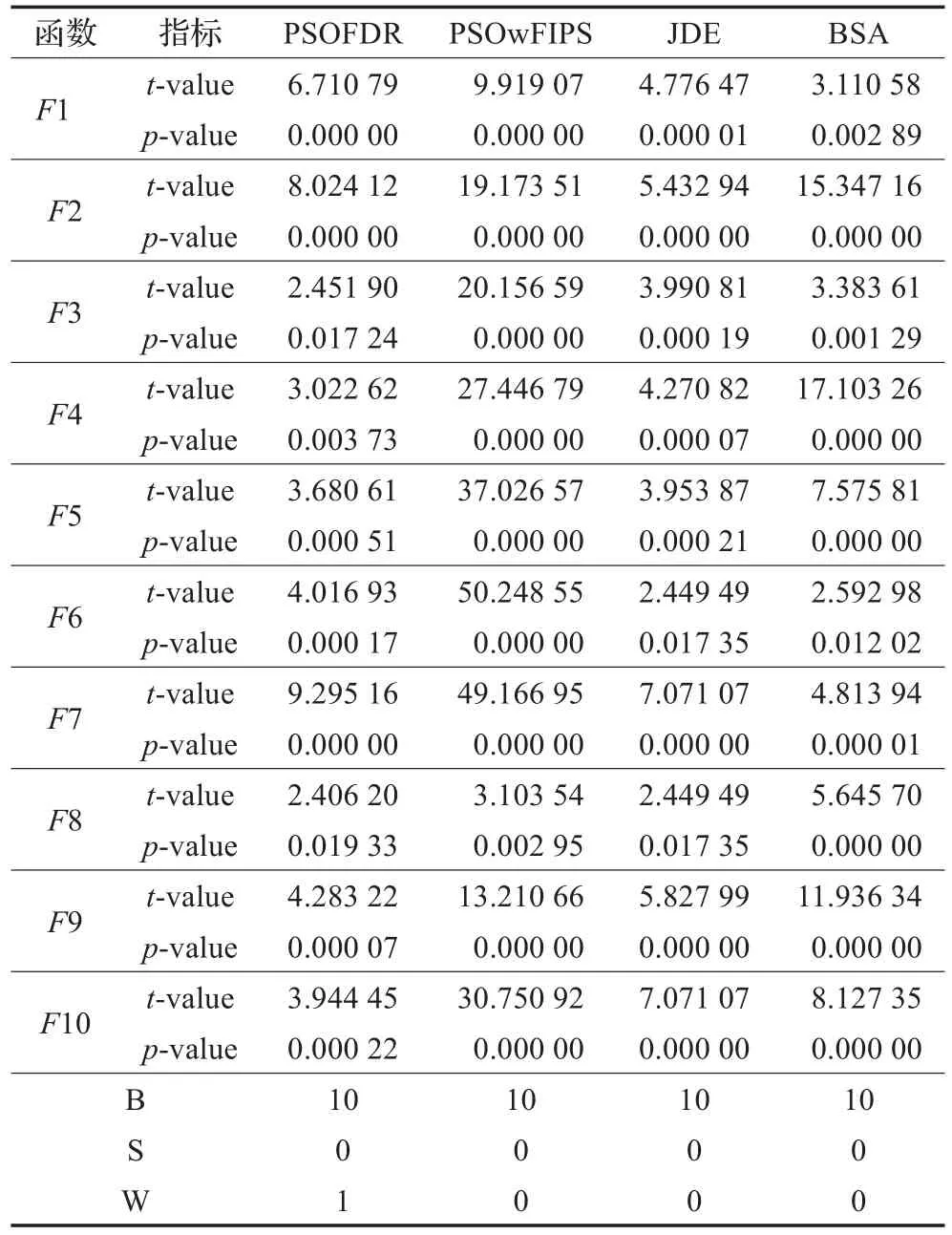
表3 GNBSA对其他4种算法的t-test结果

表4 不同m对GNBSA的测试结果

[1]Price K，Storn R M，Lampinen J A.Differential evolution：A practical approach to global optimization（natural computing series）[M].Secaucus，NJ，USA：Springer-Verlag New York Inc，2005.

[2]Kennedy J，Eberhart R.Particle swarm optimization[C]//IEEE InternationalConference on NeuralNetworks.IEEE，1995：1942-1948.

[3]Maniezzo V，Gambardella L M，Luigi F D.Ant colony optimization[J].Alphascript Publishing，2010，28（3）：1155-1173.

[4]Karaboga D，Basturk B.A powerful and efficient algorithm for numerical function optimization：Artificial bee colony（ABC） algorithm[J].Journal of Global Optimization，2007，39（3）：459-471.

[5]Qin A K，Suganthan P N.Self-adaptive differential evolution algorithm for numerical optimization[J].IEEE Congress on Evolutionary Computation，2005，2：1785-1791.

[6]Liang J J，Qin A K，Baskar S.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J].IEEE Transactions on Evolutionary Computation，2006，10（3）：281-295.

[7]段海滨，王道波.一种快速全局优化的改进蚁群算法及仿真[J].信息与控制，2004，33（2）：241-244.

[8]Zhu G，Kwong S.Gbest-guided artificial bee colony algorithm for numerical function optimization[J].Applied Mathematicsamp;Computation，2010，217（7）：3166-3173.

[9]Civicioglu P.Backtracking search optimization algorithm for numerical optimization problems[J].Applied Mathematicsamp;Computation，2013，219（15）：8121-8144.

[10]Song X，Zhang X，Zhao S，et al.Backtracking search algorithm for effective and efficient surface wave analysis[J].Journal of Applied Geophysics，2015，114：19-31.

[11]Wang L，Zhong Y，Yin Y，et al.A hybrid backtracking search optimization algorithm with differential evolution[J].Mathematical Problems in Engineering，2015，2015：1-16.

[12]Zhang C，Lin Q，Gao L，et al.Backtracking search algorithm with three constraint handling methods for constrained optimization problems[J].Expert Systems with Applications，2015，42（21）：112-116.

[13]Lin J.Oppositional backtracking search optimization algorithm for parameter identification of hyperchaotic systems[J].Nonlinear Dynamics，2015，80（1/2）：209-219.

[14]谢凯.排挤小生境遗传算法的研究与应用[D].安徽淮南：安徽理工大学，2005.

[15]Peram T，Veeramachaneni K，Mohan C K.Fitness-distanceratio based particle swarm optimization[C]//Proceedings of the 2003 IEEE Swarm Intelligence Symposium，2003（SIS’03）.IEEE，2003：174-181.

[16]Mendes R，Kennedy J，Neves J.The fully informed particle swarm：Simpler，maybe better[J].IEEE Transactions on Evolutionary Computation，2004，8（3）：204-210.

[17]Qin A K，Huang V L，Suganthan P N.Differential evolution algorithm with strategy adaptation for global numerical optimization[J].IEEE Transactions on Evolutionary Computation，2009，13（2）：398-417.

WANG Peng,CHEN Debao,ZOU Feng,LI Zheng

School of Physics and Electronic Information,Huaibei Normal University,Huaibei,Anhui 235000,China

Guidance and niching backtracking search optimization algorithm.Computer Engineering and Applications,2017,53（21）：126-131.

Backtracking Search optimization Algorithm（BSA）is a new optimization algorithm which is proposed in recent years.For the convergence speed of original BSA is slow and it is easily trapped in local optima,an improved BSA based on the combination of guidance with the best individual and niche technique is proposed to improve the global performance of it.In the method,the strategy with learning from the best individual is introduced in the mutation operator of original BSA to improve the convergence speed of it in the first.In the second,a niche repulsing technology is designed in the paper.The niching radius is determined according to the average minimal distance between every individual and the other individuals,and some parts individuals with high similarity are deleted,some new individuals are generated by a new mutation method which is designed with combining the worst information of current generation,and the new individuals are supplemented in the new population to maintain the constant number of population,the diversity of the population is increased by this operation.The convergence speed and the diversity of population is fully considered in the improved BSA,and the performance of the original BSA is largely improved.10 typical functions are used in the simulation experiments,and the results are compared with those of other algorithms.The results indicate that the improved algorithm has good performance in terms with the convergence speed and accuracy.

Backtracking Search optimization Algorithm（BSA）;guidance mechanism;niche technology;mutation strategy

A

TP301

10.3778/j.issn.1002-8331.1605-0277

国家自然科学基金（No.61572224，No.61304082）；安徽省高校自然科学研究重大项目（No.KJ2015ZD36）；安徽省高校自然科学研究重点项目（No.KJ2016A639）；安徽省国际科技合作计划项目（No.10080703003）；安徽省第七批”115”产业创新团队皖人才[2014]4号。

王鹏（1993—），男，硕士研究生，主要研究方向为智能优化计算；陈得宝（1975—），通讯作者，男，教授，博士，主要研究方向为智能计算、模式识别等，E-mail：chendb_88@163.com；邹锋（1978—），男，副教授，博士，主要研究方向为进化计算；李峥（1980—），男，副教授，主要研究方向为进化计算。

2016-05-19

2016-06-27

1002-8331（2017）21-0126-06

CNKI网络优先出版：2016-11-21,http://www.cnki.net/kcms/detail/11.2127.TP.20161121.1655.026.html