基于邻域粗糙集的实体分辨记录对划分

周 星，刁兴春，曹建军

1.解放军理工大学 指挥信息系统学院，南京 210007 2.南京电讯技术研究所，南京 210007

基于邻域粗糙集的实体分辨记录对划分

周 星1，刁兴春2，曹建军2

1.解放军理工大学 指挥信息系统学院，南京 210007 2.南京电讯技术研究所，南京 210007

现有的实体分辨方法在准确性和效率上各有所长，将易分辨和难分辨的记录对分开，为下一步分别应用不同分辨方法提供基础。对待划分的记录对，利用变精度邻域粗糙集分别计算相似记录对和不相似记录对的上下近似集，得到全体记录对的上下近似集及对应的边界，处于边界域的记录对即为难分辨的记录对，其余为易分辨的记录对。分析了变精度邻域粗糙集中的包含度阈值和距离阈值对于记录对划分的影响。利用实验比较难分辨、易分辨和原始记录对在利用相似度阈值分类和利用KNN分类时的准确性，说明了划分的有效性。

实体分辨；记录对划分；粗糙集

1 引言

实体分辨的主要任务是找出相同或不同数据源中描述同一客观实体的不同对象[1]，它通常包括三个步骤：索引、记录对比较和相似度向量分类。索引聚合可能重复的记录以提升分辨效率；记录对比较运用字段相似度函数计算记录对各个字段的相似度，生成字段相似度向量；相似度向量分类根据字段相似度向量将记录对分为匹配、不匹配和可能匹配[2]，其中可能匹配是指记录对可能为匹配，也可能为不匹配，通常需要专家参与以进一步确定。这类方法又称为基于属性的方法（Feature Based Similarly，FBS）。

Kalashnikov等为提高实体分辨的准确性，提出了一种基于关联关系的数据清洗（Relationship-based Data Cleaning，RelDC）方法，他利用无向图对数据库进行建模，得到实体关系图，再利用实体之间的关系进行分辨[3-4]。

曹建军等比较了FBS和RelDC方法，指出FBS方法效率较高，但是在某些记录对上的分辨准确性较低，RelDC准确性较高，但是由于需要构建实体关系图，复杂性较高，因此他指出需要构建一种选择方法，即为难分辨的记录对选择RelDC方法，为其余记录对选择FBS方法[5]，这种选择的前提是区分难分辨的记录对和易分辨的记录对。

文献[6]为发现难分辨的记录对，构建了一个多分类器，当对某个记录对，分类器的投票出现最大分歧，即判断该记录对为相似和不相似的分类器一样多时，该记录对为难分辨的记录对，它能提供最大的信息增益。该方法由于采用了多分类器，分辨出的记录对与具体算法有关，且计算复杂性较高。

文献[7]首先利用云模型[8]计算各记录相似度对应相似或不相似概念的置信度，根据置信度求出相似记录对和不相似记录对的记录相似度阈值，并认为大于相似记录对的记录相似度阈值，则为相似；小于不相似记录对的记录相似度阈值，则为不相似；二者之间的则既可能为相似也可能为不相似，对应记录对为难分辨的记录对。但是云模型假设了记录相似度呈近似正态分布，并且其仅通过记录相似度来判断记录对是否相似，仅能发现线性可分或不可分的情况，不能发现非线性可分或不可分的情况。

文献[9]假设记录相似度呈正态分布，并利用三倍方差选择难分辨的记录对，即记录相似度大于相似记录对的记录相似度的均值减去三倍方差，则认为相似，记录相似度小于不相似记录对的记录相似度的均值加上三倍方差，则认为不相似。这种方法的好处是实现简单，但是缺点不仅和文献[7]中的一样，而且记录相似度呈正态分布的假设还更为严格。

粗糙集中的边界域[10]表示根据已有知识，不能明确属于哪一类的样本，它不需要假设样本的分布，且所求出的难以分类的样本与学习算法无关，效率较高，因此本文选择粗糙集对记录对进行划分。

由于实体分辨中，字段相似度为[0，1]区间的连续值，因此本文采用文献[11]中提出的邻域粗糙集查找难分辨的记录对。

2 邻域粗糙集

粗糙集用一个四元组S=(U,A,V,f)表示一个信息系统，其中U是一个称为论域的非空有限对象集合，A是一个非空有限属性集合，V=∪a∈AVa，Va是属性a的值域，f:U×A→V是一个从论域U，属性集合A到值域V的信息函数。当A=C⋃D，C是条件属性集合，D是决策属性集合时，该信息系统称为决策信息系统[12]。

对于离散值，每一个非空子集B都决定了一个不可分辨关系，RB={(x,y)∈U×U|f(x,a)=f(y,a),∀a∈B}，其中U是论域，B是属性集合，x，y是论域上的对象，不可分辨关系是粗糙集理论的基础；对于连续值，利用邻域关系将不可分辨关系扩展为：RB={(x,y)∈U×U|Δa(x,y)≤δ,∀a∈B}，其中 B 是属性集合，Δ 是距离函数，δ是距离阈值。应用邻域关系的决策信息系统称为邻域决策信息系统。

给定邻域决策信息系统S=(U,C⋃D,V,f)，令X1,X2,…,XN为对应决策1到N的对象集合，δB(xi)={y∈U|Δa(x,y)≤δ,∀a∈B}为 xi在特征空间 B⊂C 上的邻域对象集合，D相对于属性集合B的下近似集和上近似集的定义如下[11]：

其中

该定义对于噪声比较敏感，因此，文献[13]提出了变精度粗糙集，它引入包含度对邻域粗糙集进行泛化。给定论域中的两个集合A、B，包含度的定义如下：

D相对于属性集合B的决策边界域定义为[9]：

其中A≠∅，||⋅为集合的基。

此时，X的上下近似的定义为：

其中，k称为包含度阈值，取值范围为0.5≤k≤1。

3 基于邻域粗糙集的记录对划分

本文利用变精度邻域粗糙集求解记录对的边界域，并认为处于边界域的记录对为边界记录对，对应难分辨的记录对；余下的记录对为正常记录对，对应易分辨的记录对。其算法流程如下：

输入 匹配记录对M和不匹配记录对U，包含度阈值k，距离阈值δ。

步骤1计算匹配记录对M和不匹配记录对U的字段相似度向量X1和X2。

步骤2根据公式（5）分别计算 X1和X2的上下近似集

步骤4根据公式（3）计算边界域，以及处于边界域的记录对BR，余下为正常域内的记录对NR。

输出 BR和NR。

算法过程即是首先分别求出相似记录对和不相似记录对的上下近似集，再得到全体记录对的上下近似集，最后根据定义，求出边界域。

变精度和邻域关系的引入将导致找出的边界域的记录对为难分辨的记录对的置信度下降。对于变精度粗糙集，包含度阈值k的影响较大，k越大，正常域里的记录对属于易分辨的记录对的置信度越高，但是将使得边界记录对占比 pr过大，其中

另一方面，邻域关系对置信度影响也较大。当距离阈值δ为0时，仅完全相同的记录对被判定为相似，因此所有记录对均为正常记录对，此时两个记录对同为相似或不相似的置信度最高，pr为0。距离阈值δ越小，置信度越大，但是也将导致 pr过大。

为说明包含度阈值k和距离阈值δ与边界记录对占比 pr的关系，以文献[14]中的amazon_gp数据集为例。使δ在0～0.5以0.02的步长进行变化，k在0.5～1以0.02的步长进行变化，计算相应的pr，得出如图1所示的关系。

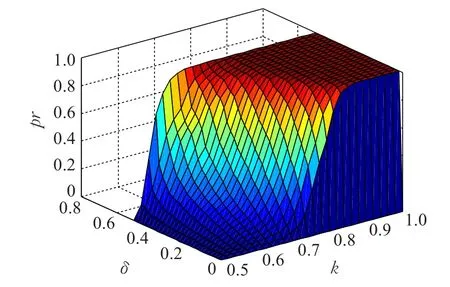
图1 边界记录对占比pr和包含度阈值k及距离阈值δ的关系

从图1可知，pr与k呈递增关系，且随着δ增加，pr相对k增长更快。然而，并不是所有的记录对都呈现严格递增关系，部分记录对存在波动。

综合来看，k趋于1，δ趋于0时，利用粗糙集查找出的边界记录对确为难分辨记录对的置信度最高。如果记录对中难分辨记录对过多，可以选择将δ设置为尽量小；如果为了使求出的边界记录对不要太多，可以将k设置较小。

4 实验

本文采用文献[14]中用到的dblp_acm、abt_buy和amazon_gp数据集。对数值型字段，利用sim(a,b)=计算相似度，对字符型字段，利用Jaccard相似度[15]计算相似度，将相似记录对的类标设为1，不相似记录对的类标设为-1，根据各数据中的 pr和k及δ的关系，选择合适的k和δ。

为比较记录对划分对实体分辨的影响，将记录对分为正常记录对、边界记录对和原始记录对，比较各组记录对在利用相似度阈值分类和利用KNN分类时的准确性，以说明记录对划分的有效性。利用相似度阈值分类，即认为相似度大于该阈值则为相似，小于该阈值则为不相似。利用KNN分类，即利用KNN算法将记录对分为相似和不相似两类。

实验环境为1台i7-4790 CPU，4 GB内存的PC，实验平台为MATLAB7.0。

4.1 记录对划分对记录相似度阈值的影响

为比较记录对划分对利用相似度阈值分类的影响，利用线性回归计算各字段的权重，将各字段相似度加权得到记录相似度。

利用MATLAB画出正常记录对、边界记录对和原始记录对中的相似记录对和不相似记录对的记录相似度的散点图，以直观、定性地表示记录对划分对用相似度阈值进行分类的影响。

测试记录对的参数及对应的pr如表1所示。

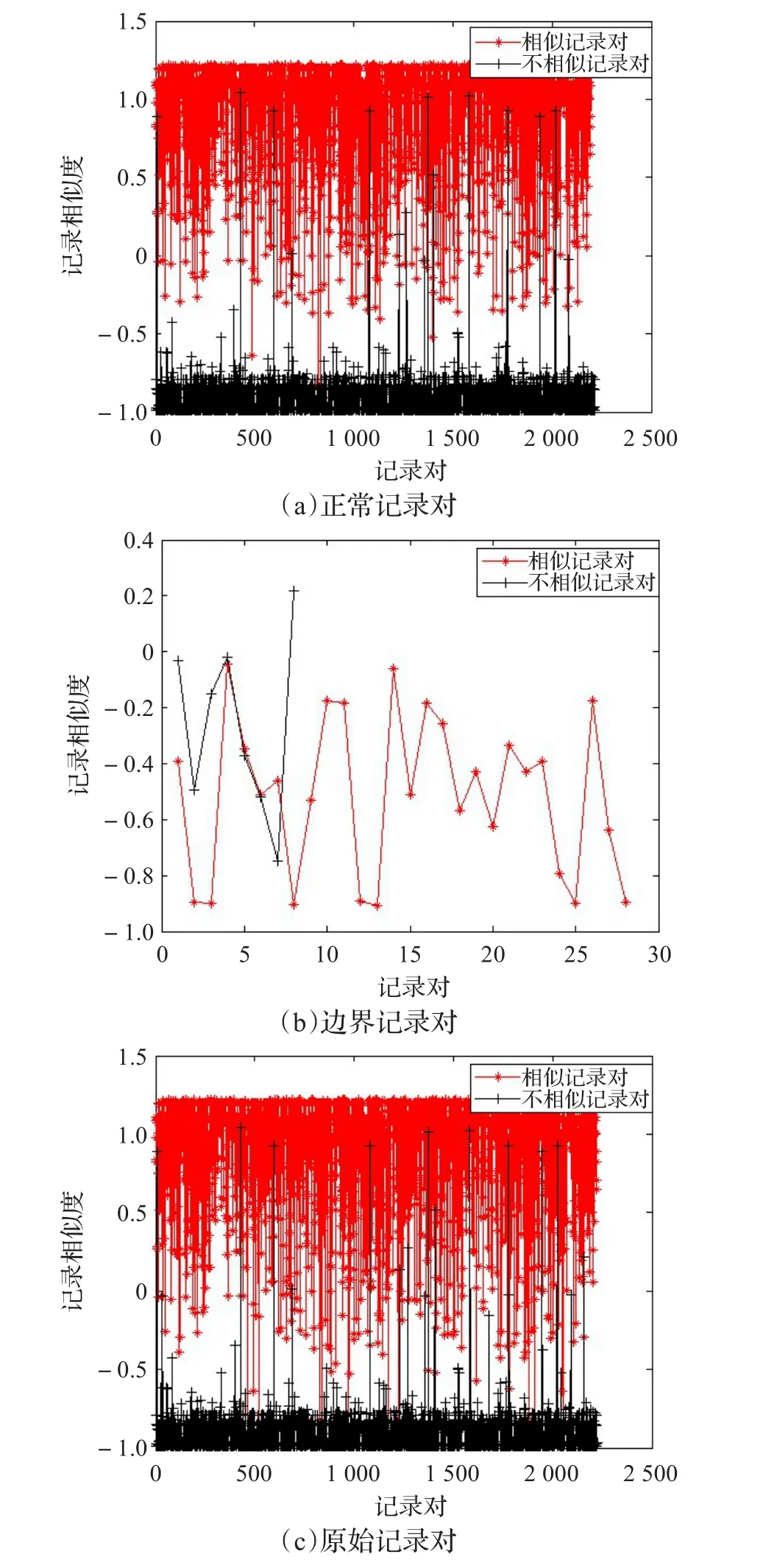
图2 dblp_acm的记录相似度比较

从图2～4可知，尽管由于变精度的存在，位于正常域的记录对，相似记录对和不相似记录对的记录相似度存在部分交叉，但是相比原始记录对，存在交叉的记录对已经大幅减少，更有利于用相似度阈值进行分类；而边界域的记录对存在交叉的变多，更难用相似度阈值进行分类。

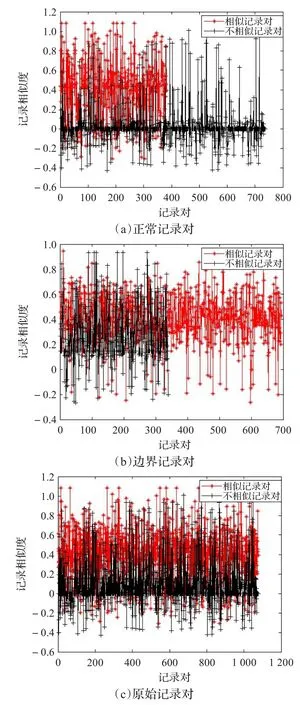
图3 abt_buy的记录相似度比较

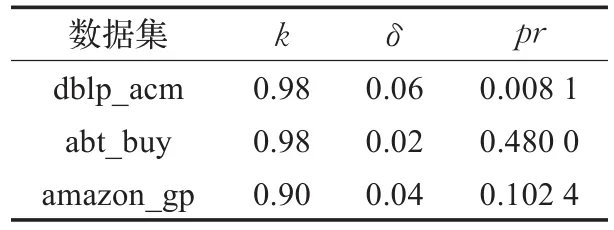
表1 测试记录对的参数及对应的pr

4.2 记录对划分对分类正确率的影响

对正常记录对、边界记录对和原始记录对，分别利用KNN分类器运行10轮5折交叉检验验证分类的准确性，取K 为5。

对各记录对，求出分类正确率的均值和标准差，并采用置信度为0.05的双边t检验，将正常记录对、边界记录对与原始记录对进行对比，若结果明显好（差），则用●（○）标记，最好的结果加粗表示，最后一行表示win/tie/loss统计结果。正确率比较如表2所示。

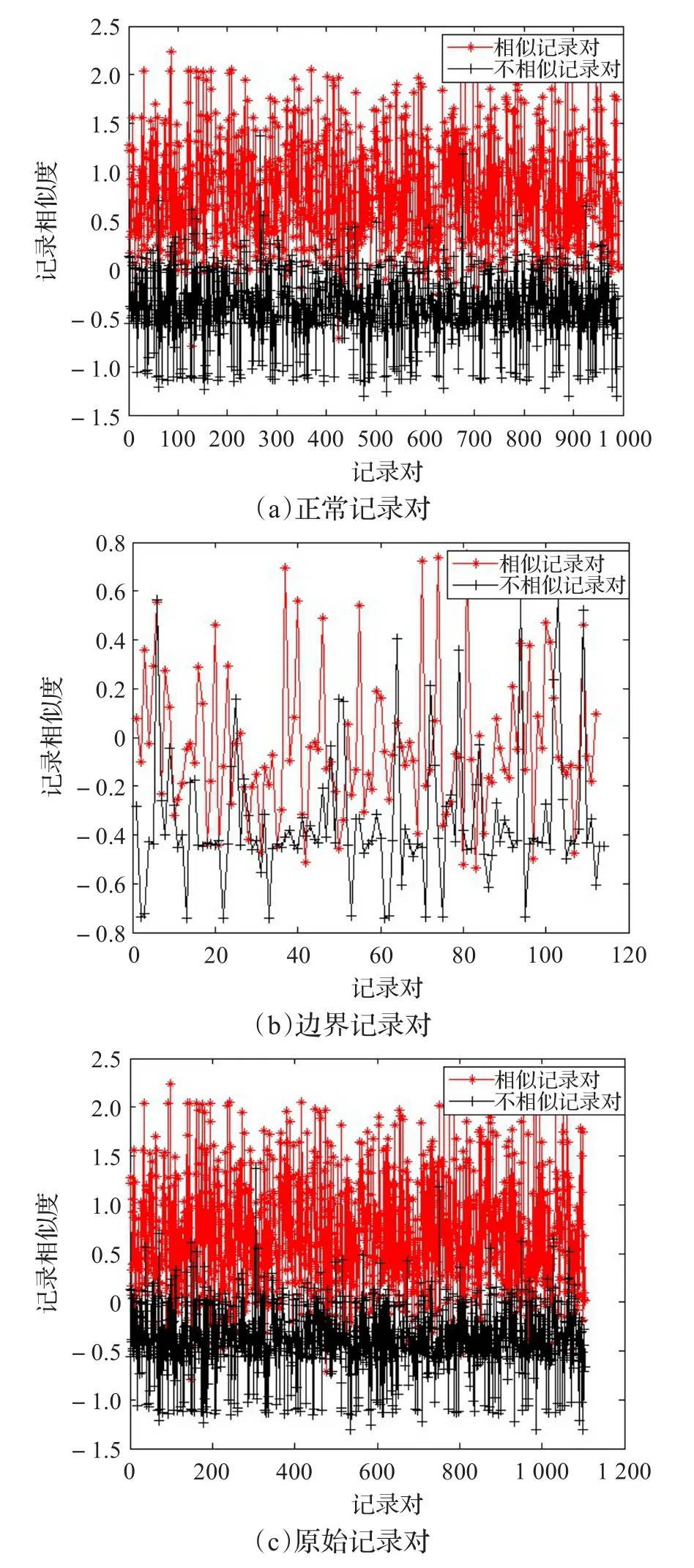
图4 amazon_gp的记录相似度比较

表2 分类正确率比较

从表2可知，正常记录对相比原始记录对，分类正确率得到了提高，而边界记录对相比原始记录对，分类正确率显著降低，进一步说明了记录对划分的有效性。

5 结论

本文利用变精度邻域粗糙集对实体分辨记录对进行划分，为对易分辨的记录对和难分辨的记录对分别应用不同的分辨方法提供基础。分析了变精度邻域粗糙集中的包含度阈值和距离阈值对于记录对划分后边界记录对占比的影响，为每个记录对选择合适的参数。比较各组记录对在利用相似度阈值分类和利用KNN分类时的准确性，说明方法的有效性。

[1]Elmagarmid A K，Ipeirotis P G，Verykios V S.Duplicate record detection：A survey[J].IEEE Transactions on Knowledge and Date Engineering，2007，19（1）：1-16.

[2]Christen P.A survey of indexing techniques for scalable record linkage and deduplication[J].IEEE Transactions on Knowledge and Date Engineering，2012，24（5）：1537-1555.

[3]Kalashnikov D V，Mehrotra S.Domain-independent data cleaning via analysis of entity-relationship graph[J].ACM Transactions on Database Systems，2006，31（2）：716-767.

[4]Kalashnikov D V，Nuray-Turan R，Mehrotra S.Adaptive connection strength models for relationship-based entity resolution[J].ACM Journal of Data and Information Quality，2012，4（2）.

[5]曹建军，刁兴春，汪挺，等.领域无关记录对清洗研究综述[J].计算机科学，2010，37（5）：26-29.

[6]Tejada S，Knoblock C A，Minton S.Learning domainindependent string transformation weights for high accuracy identification[C]//ACM SIGKDD，Edmonton，2002.

[7]Zhou Xing，Diao Xingchun，Cao Jianjun.A data cleaning switch technology based on cloud model[C]//International Conference on Information Quality，Xi’an，China，2014.

[8]李德毅，刘常昱，杜鹢，等.不确定性人工智能[J].软件学报，2004，15（11）：1583-1594.

[9]Zhou Xing，Diao Xingchun，Cao Jianjun.A high accurate multiple classifier system for entity resolution using resampling and ensemble selection[J].Mathematical Problems in Engineering，2015（2）：1-6.

[10]Pawlak Z.Rough sets[J].International Journal of Computer and Information Sciences，1982，11（5）：341-356.

[11]Hu Qinghua，Yu Daren，Liu Jinfu，et al.Neighborhood rough set based heterogeneous feature subset selection[J].Information Sciences，2008：3577-3594.

[12]Liang Jiye，Wang Feng，Dang Chuangyin，et al.A group incremental approach to feature selection applying rough set technique[J].IEEE Transactions on Knowledge and Data Engineering，2014，26（2）：294-308.

[13]Ziarko W.Variable precision rough sets model[J].Journal of Computer and System Sciences，1993，46（1）：39-59.

[14]Papadakis G，Koutrika G，Palpanas T，et al.Meta-blocking：Taking entity resolution to the next level[J].IEEE Transactions on Knowledge and Data Engineering，2014，26（8）：1946-1960.

[15]Xiao Chuan，Wang Wei，Lin Xuemin，et al.Efficient similarity joins for near-duplicate detection[J].ACM Transactions on Database Systems，2011，36（3）.

ZHOU Xing1,DIAO Xingchun2,CAO Jianjun2

1.School of Command Information System,PLA University of Science and Technology,Nanjing 210007,China 2.Nanjing Telecommunication Technology Institute,Nanjing 210007,China

Record pairs partition for entity resolution based on neighborhood rough set.Computer Engineering and Applications,2017,53（21）：72-76.

The present approaches of entity resolution vary in effectiveness and efficiency,normal record pairs and ambiguous record pairs are separated,so that different approaches can be applied to them.As to the record pairs to be partitioned,variable precision neighborhood rough set is used to compute the lower and upper approximation of similar record pairs and dissimilar record pairs respectively,to get the approximation sets and boundary region of all record pairs,and those record pairs in the boundary region are regarded as ambiguous,the rest are normal.How the thresholds of inclusion degree and distance in the variable precision neighborhood rough set affect the effectiveness of data partition is analyzed.Experiments are conducted to compare the accuracy of the normal,ambiguous and original record pairs while using similarity threshold and KNN to resolute,showing the effectiveness of partition.

entity resolution;record pair partition;rough set

A

TP311

10.3778/j.issn.1002-8331.1605-0266

国家自然科学基金（No.61070174）。

周星（1988—），男，博士生，主要研究方向为数据工程、数据质量，E-mail：zx0327@163.com；刁兴春（1964—），男，研究员，博士生导师，主要研究方向为数据工程；曹建军（1975—），男，博士，硕士生导师，主要研究方向为数据质量、进化算法。

2016-05-19

2016-07-19

1002-8331（2017）21-0072-05

CNKI网络优先出版：2016-11-21,http://www.cnki.net/kcms/detail/11.2127.TP.20161121.1655.024.html