属性值细化的矩阵增量约简算法

李 丹

成都东软学院 计算机科学与技术系，四川 青城山 611844

属性值细化的矩阵增量约简算法

李 丹

成都东软学院 计算机科学与技术系，四川 青城山 611844

现实生活中许多数据库都是动态变化的，为了获取新的知识，传统的方法需要重复计算，耗时巨大。为了克服这个缺陷，有效处理动态数据，许多学者提出了增量学习方法。针对决策表属性值动态变化，提出了基于属性值细化的矩阵增量约简算法，当一部分属性值被细化时，同非增量约简方法相比，增量方法能快速找到新的约简，最后通过UCI数据进行性能测试，实验仿真结果表明所提增量约简算法是有效的。

属性值细化；增量学习；属性约简；粗糙集；知识粒度

1 概述

在现实生活中，许多领域的数据如经济研究、社会调研和医药研究的数据都是动态变化的，使用传统获取知识的方法处理这些数据需要重复操作才能获得新知识，重复操作造成时间消耗巨大，故传统获取知识的方法处理动态数据效果不好。为了克服这些缺陷，有效处理动态数据，许多研究者提出了增量学习方法，该方法能够有效利用以前的知识，不需要对全部数据重新学习，这在一定程度上更能满足实际需要。属性约简也称为特征选择，它是数据处理的一种有效技术，已经被广泛应用到模式识别、数据挖掘、机器学习领域，研究者提出了很多属性约简的方法[1-3]，但是这些方法都是处理静态数据集的，对于动态变化的数据需要重复计算，造成时间和空间的浪费。

增量约简算法可以有效处理动态数据，科学研究者对动态约简方法已做了大量的工作。Zeng等在模糊决策信息系统中，研究了属性集添加或删除时，近似空间中知识粒度的变化规律，提出了属性集动态变化时动态特征提取方法[4]；王磊等从矩阵的视角探讨信息系统动态知识更新的有效方法和途径，提出了信息系统的属性值发生变化时变精度粗糙集模型中概念上、下近似集增量式更新的矩阵方法并构造出相应的算法[5]；Wang等根据三种信息熵概念，定义了信息熵增量机制，针对属性值动态变化情况，提出了一种有效特征选择方法[6]；刘洋等构造了差别矩阵的增量机制，在对象动态增加下，提出了一种基于差别矩阵的增量约简完备算法[7]；Luo等在集值有序决策系统中，构造了基于矩阵的上、下近似集计算方法，并提出了属性泛化时近似集的动态更新算法，利用UCI公共数据集测试了算法的性能[8]；Chen等在不完备信息系统中，定义了最小辨识属性集，并在属性值粗化细化时，分析了最小辨识属性集及规则的演化性质，提出了不协调决策系统中基于粗糙集的规则增量更新算法[9]。Jing等分析了属性增加时知识粒度的增量机制，提出了增量属性约简算法[10]；针对决策粗糙集模型，Luo等提出了矩阵计算近似集的增量算法[11]；Jing等分析了对象增加时知识粒度的增量机制，提出了基于知识粒度的增量约简方法[12]；Shu等针对不完备信息系统，提出了基于正区域的增量约简算法[13]；针对对象变化时，Liang等提出了基于信息熵的增量约简算法[14]。根据上面分析，基于属性值细化的矩阵增量式约简算法研究较少。

矩阵是一种非常强大的数学工具，它的特点是直观和简明，在工程和科学研究领域应用比较广泛。知识粒度在粗糙集中用来表示信息的不确定程度，许多研究者已经把它应用到启发式属性约简中，在现实生活中，许多数据库的数据都是动态变化的，静态约简算法在处理这些数据会消耗巨大的时间和空间，为了提高计算速度，本文提出了一种属性值细化的矩阵增量式约简算法，当决策表的某些属性发生细化时，给出了知识粒度的增量机制，使用UCI数据集对该算法进行了测试，实验结果表明所提的增量算法是有效的。

2 粗糙集的相关知识

定义1[15]假设一个信息系统S=(U,A=C⋃D,V,f)是四元组，U为论域，C为条件属性集且D为决策属性集，，其中Va为属性a的值，f:U×C⋃D→V 是信息函数，且a∈C⋃D，x∈U有 f(x,a)∈Va。

定义2[1]假设S=(U,A=C⋃D,V,f)是一个决策表，U 为论域且U/C={X1,X2,…,Xm}，条件属性C的知识粒度被定义为

3 知识粒度约简算法

3.1 知识粒度基本知识

定义3[5]假设S=(U,A=C⋃D,V,f)是一个决策表，且U/C={X1,X2,…,Xm}，RC是U 的一个等价关系，则关系矩阵的元素被定义为：

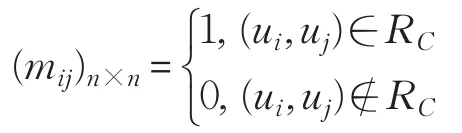
定义4[16]假设S=(U,A=C⋃D,V,f)是一个决策表，且U/C={X1,X2,…,Xm}，条件属性C的知识粒度被定义为是关系矩阵的平均值。

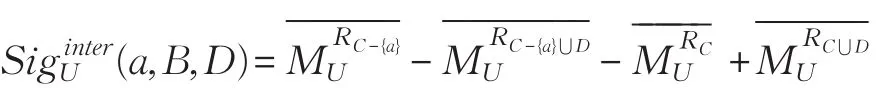
定义8[1]假设S=(U,A=C⋃D,V,f)是一个决策表，决策表S的核被定义为C,D)＞ 0}。

定义9[1]假设S=(U,A=C⋃D,V,f)是一个决策表，B⊆C，B为决策表S的属性约简当且仅当：

（1）GD(D|B)=GD(D|C)；

（2）对于∀a∈B，使得GD(D|B-{a})≠GD(D|C)。

3.2 基于知识粒度的启发式约简算法

根据上面定义的矩阵表示形式，构造了一种基于知识粒度的启发式约简算法1描述如下：

算法1基于矩阵的启发式约简算法

输入 决策表S=(U,A=C⋃D,V,f)；

输出 属性约简REDU。

步骤1根据定义8计算S的核CoreC(D)，REDU←CoreC(D)。

步骤2如果GDU(D|REDU)=GDU(D|C)，转跳到步骤5，否则转跳到步骤3。

步骤3P←REDU，当GDU(D|P)≠GDU(D|C)，计算属性a(a∈C-P)相对于属性P的重要性（符合定义7），依次循环选取重要性最大的属性a0=max(SigoutterU(a,P,D))添加到P中，即P←P⋃{a0}，直到GDU(D|P)=GDU(D|C)为止。

步骤4从后向前依次遍历P中的每一个属性a，计算知识粒度GDU(D|P-{a})，如果GDU(D|P-{a})=GDU(D|C)，则 P←P-{a}。

步骤5REDU←P，输出S属性约简REDU，算法结束。

4 基于属性值细化的矩阵增量式约简算法

4.1 知识粒度的增量机制

当信息系统的属性值发生细化时，用算法1计算新决策表的属性约简需要重复计算知识粒度，造成时间和空间消耗巨大。为了提高计算速度，在较短的时间内快速找到新决策表的属性约简，提出了一种基于属性值细化的矩阵增量式约简算法。

定义10[5]S=(U,A=C⋃D,V,f)是一个决策表，B⊆A,B≠∅,al∈B ，其中属性 al的值域为 Vl，若有 f(xk,al)=v，且v∉Vl，则称属性值 f(xi,al)=v细化为v。

记 IX-Y={i|ui∈X-Y}，IY={i|ui∈Y}，其中 IX-Y表示集合X-Y中元素下标组成的集合，IY表示集合Y中元素下标组成的集合。

定义11[5]S=(U,A=C⋃D,V,f)是一个决策表，是U 的关系矩阵。假设属性ai的属性值发生细化，U′表示新的论域，则细化后的关系矩阵的元素被定义为：

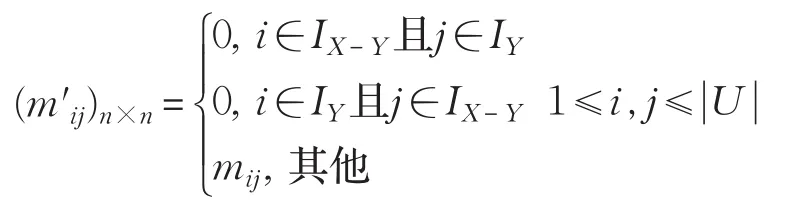
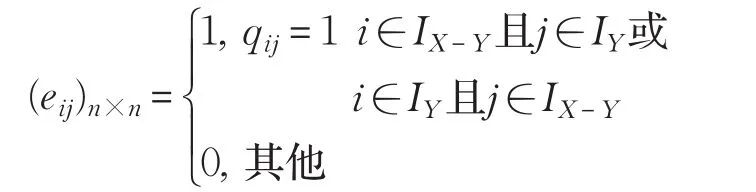
定理1S=(U,A=C⋃D,V,f)是一个决策表，GDU(C)是决策表条件属性C的知识粒度。假设属性ai的属性值发生细化，U′表示新的论域，增量关系矩阵为则决策表的知识粒度为：

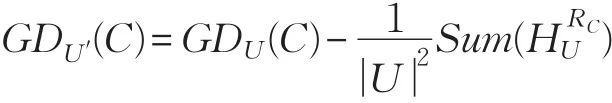
定理2S=(U,A=C⋃D,V,f)是一个决策表，GDU(C⋃D)是决策表条件和决策属性C⋃D的知识粒度。假设属性ai的属性值发生细化，U′表示新的论域，增量关系矩阵为则决策表的知识粒度为：

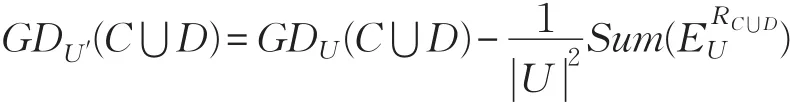
定理3S=(U,A=C⋃D,V,f)是一个决策表，GDU(D⋃C)是条件属性C关于决策属性D的相对知识粒度。假设属性ai的属性值发生细化，U′表示新的论域，增量关系矩阵为，则属性C关于D的相对知识粒度为：

4.2 属性值细化的矩阵增量约简算法

根据上面所提的知识粒度的增量机制，提出了一种基于属性值细化的矩阵增量式约简算法2，假设有一个动态决策表，当某些属性的值发生了细化，首先利用知识粒度增量机制计算变化后新决策表的知识粒度，然后在原来决策表约简的基础上，可以快速找到细化后决策表的约简，算法2描述如下：

算法2一种属性值细化的矩阵增量约简算法

输入 决策表S=(U,A=C⋃D,V,f)，属性P细化前的约简REDU，属性P的值发生了细化。

输出 属性P的值细化后的约简REDU′。

步骤1B←REDC，计算增量关系矩阵

步骤2计算属性P的值发生了细化后的知识粒度GDU′(D|B)，GDU′(D|C)（根据定理1～3）。

步骤 3 如果 GDU′(D|B)=GDU′(D|C)，转跳到步骤6，否则转跳到步骤4。

步骤4 当 GDU′(D|B)≠GDU′(D|C)，计算属性 a(a∈C-B)相对于属性B的重要性（符合定义7），依次循环选取重要性最大的属性添加到 B 中，即 B←B⋃{a0}，直到 GDU′(D|B)=GDU′(D|C)为止。

步骤5从后向前依次遍历B中的每个属性a，计算 知 识 粒 度 GDU′(D|B-{a}) ，如 果 GDU′(D|B-{a})=GDU′(D|C)，则 B ←B-{a}。

步骤6REDU′←B，输出属性 P细化后的约简REDU，算法结束。

下面对算法1（非增量算法）和算法2（增量算法）的时间复杂度进行分析，当决策表的某个属性被细化后，非增量约简算法的时间复杂度近似为O(|C||U|2)，而增量约简算法的时间复杂度近似为O(|C||X-Y||Y|)，因为|X-Y||Y|＜|U|2，所提的矩阵增量约简算法计算时间小于非增量约简算法所花费的时间。

5 实验分析

为了测试本文提出算法2的性能，把算法2的约简时间和算法1的约简时间作比较，并从UCI数据集选取Lung Cancer和 ticdata2000作为实验仿真数据集，数据集描述如表1，实验仿真的环境：CPU Pentium®Dual-Core E5800 3.20 GHz，内存：Samsung DDR3 SDRAM，4.0 GB Windows7操作系统，32 bit(JDK1.6.0_20)。

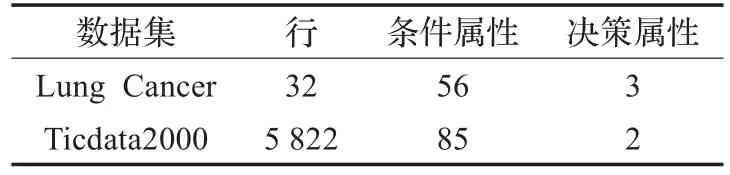
表1 数据集描述

在实验仿真过程中，把每个数据集均分成两部分，其中有一部分作为基本数据集，分别对另一部分数据集的10%、20%、30%、40%、50%数据的属性值进行细化，分别用增量约简算法和非增量约简算法运行每个数据集，实验结果如图1所示，纵轴表示算法的计算时间，横轴表示数据集对象属性值细化的百分数。

通过实验仿真结果可以得出，所提属性值细化的矩阵增量约简算法的计算时间远远小于非增量约简算法的计算时间，从而说明本文所提的属性值细化的矩阵增量约简方法是有效的。

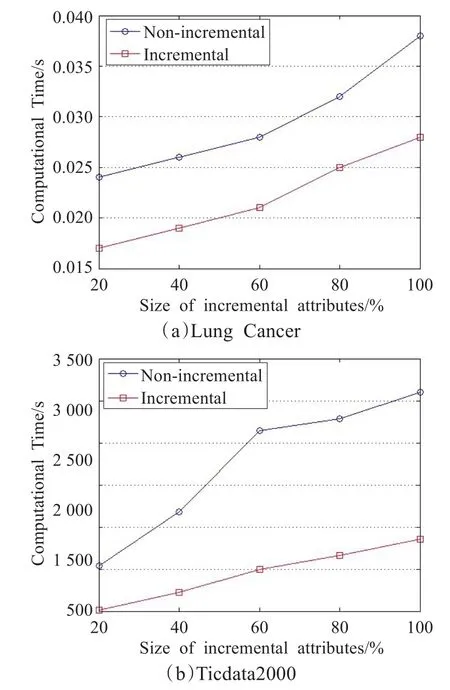
图1 插入多个属性集增量和非增量约简算法消耗时间的比较

6 结论

动态数据约简算法研究是人工智能领域中的一个研究热点，本文根据知识粒度的矩阵表示方法，提出了一种属性值细化的矩阵增量约简算法，当决策表的属性值发生细化时，首先通过增量机制来更新属性值细化后决策表的知识粒度，然后在原有约简的基础上，可以快速找到新的约简，通过与非增量约简算法的比较，实验结果表明增量属性约简的方法是可行的。下一步研究将考虑在云计算环境平台下如何实现并行增量的属性约简算法。

[1]苖夺谦，范世栋.知识粒度的计算及其应用[J].系统工程理论与实践，2002，22（1）：48-56.

[2]王国胤，于洪，杨大春.基于条件信息熵的决策表约简[J].计算机学报，2002，25（7）：760-765.

[3]梁吉业，曲开社，徐宗本.信息系统的属性约简[J].系统工程理论与实践，2001，21（12）：76-80.

[4]Zeng Anping，Li Tianrui，Liu Dun，et al.A fuzzy rough set approach for incremental feature selection on hybrid information systems[J].Fuzzy Sets and Systems，2014，258：39-60.

[5]王磊，洪志全，万旎.属性值变化时变精度粗糙集模型中近似集动态更新的矩阵方法研究[J].计算机应用研究，2013，30（7）：2011-2013.

[6]Wang Feng，Liang Jiye，Dang Chuangyin.Attribute reduction for dynamic data sets[J].Applied Soft Computing，2012，18：1-18.

[7]刘洋，冯博琴，周江卫.基于差别矩阵的增量式属性约简完备算法[J].西安交通大学学报，2007，41（2）：158-161.

[8]Luo Chuan，Li Tianrui，Chen Hongmei.Dynamic maintenance of approximations in set-valued ordered decision systems under the attribute generalization[J].Information Sciences，2014，257：210-228.

[9]Chen Hongmei，Li Tianrui，Luo Chuan，et al.A rough set-based method for updating decision rules on attribute values coarsening and refining[J].IEEE Transactions on Knowledge and Data Engineering，2014，26（12）：2886-2899.

[10]Jing Yunge，Li Tianrui，Huang Junfu，et al.An incremental attribute reduction approach based on knowledge granularity under the attribute generalization[J].International Journal of Approximate Reasoning，2016，76：80-95.

[11]Luo Chuan，Li Tianrui，Zhang Yi，et al.Matrix approach to decision-theoretic rough sets for evolving data[J].Knowledge-Based Systems，2016，99：123-134.

[12]Jing Yunge，Li T R，Luo C，et al.An incremental approach for attribute reduction based on knowledge granularity[J].Knowledge-Based Systems，2016，104（C）：24-38.

[13]Shu Wenhao，Shen Hong.Updating attribute reduct in incomplete decision systems with the variation of attribute set[J].International Journal of Approximate Reasoning，2014，55：867-884.

[14]Liang Jiye，Wang Feng，Dang Chuangyin，et al.A group incremental approach to feature selection applying rough set technique[J].IEEE Transactions on Knowledge and Data Engineering，2014，26（2）：1-31.

[15]刘清.Rough set及Rough理论[M].北京：科学出版社，2001：7-16.

[16]王磊，叶军.知识粒度计算的矩阵方法及其在属性约简中的应用[J].计算机工程与科学，2013，35（3）：98-102.

LI Dan

Department of Computer Science and Technology,Chengdu Neusoft University,Qingchengshan,Sichuan 611844,China

Matrix-based incremental reduction approach with attribute values refining.Computer Engineering and Applications,2017,53（21）：68-71.

In practices,many real data in databases may vary dynamically.One has to run a knowledge acquisition method repeatedly in order to acquire new knowledge.This is very time-consuming.To overcome this deficiency,incremental approaches have been presented to deal with dynamic data set.This paper proposes a matrix-based incremental reduction approach with attribute values refining.When a part of data in a given data set is replaced by some new data,compared with the non-incremental reduction approach,the developed incremental reduction approach can find a new reduct in a much shorter time.Finally,experiments on two data sets downloaded from UCI show that the developed algorithm is effective.

attribute values refining;incremental learning;attribute reduction;rough set;knowledge granularity

A

TP18

10.3778/j.issn.1002-8331.1605-0246

国家自然科学基金联合项目（No.U1230117）。

李丹（1973—），男，讲师，研究方向：粒计算，云计算，移动应用开发，E-mail：lidan@nsu.edu.cn。

2016-05-18

2016-06-28

1002-8331（2017）21-0068-04

CNKI网络优先出版：2016-11-21,http://www.cnki.net/kcms/detail/11.2127.TP.20161121.1652.020.html