基于拟蒙特卡洛的半不变量法概率潮流计算

栗然，范航，张凡，靳保源

(新能源电力系统国家重点实验室(华北电力大学)，河北省保定市 071003)

基于拟蒙特卡洛的半不变量法概率潮流计算

栗然，范航，张凡，靳保源

(新能源电力系统国家重点实验室(华北电力大学)，河北省保定市 071003)

随着风电并网容量的增加，概率潮流计算方法在计及风电出力不确定性的同时，还需考虑邻近风电场由于风速相关性导致的风电出力相关性问题。针对风电出力波动范围较大且存在相关性的特点，提出一种可考虑输入变量相关性的基于拟蒙特卡洛的半不变量法概率潮流计算方法。该方法利用基于Nataf变换的拟蒙特卡洛法产生具有相关性的风电出力样本，在各样本点处进行半不变量法概率潮流计算，基于各风电出力样本下的状态变量正态分布特性，依全概率公式整合所得正态分布得到最终的概率潮流结果。基于IEEE 30节点系统的算例分析表明，所提方法在较小采样规模下具有很高的计算精度，能够较精确地得到系统状态变量的概率分布。

概率潮流; 半不变量法; 拟蒙特卡洛; 风电并网

0 引 言

电力系统实际运行时存在大量不确定因素，如负荷的波动、发电机的停运、线路等元件的随机故障。此外，风力发电、光伏发电作为清洁型发电形式在我国得到大力发展，这种间歇性能源的大规模并网将增强电力系统的不确定性。确定性潮流计算只能得到系统确定工况下的潮流分布，不能全面反映系统运行状态。而概率潮流[1]作为可评估不确定因素对系统影响的有效工具，已得到广泛的研究。

目前，概率潮流计算主要分为3类[2]：模拟法[3]、近似法[4]和解析法[5]。模拟法基于蒙特卡洛抽样，计算过程直观，当样本容量足够大时，计算结果精度很高。但在提高精度的同时，蒙特卡洛模拟法计算规模往往很大，因此成为评估其他方法准确性的基准。近似法又分为点估计法、一次二阶距法和状态变换法。近似法在计算输出随机变量的期望和方差时较为有效，但很难得到准确的整体概率分布[2]。解析法以半不变量法为代表，半不变量法利用累计量进行卷积运算，再通过级数展开或最大熵原理得到输出随机变量的概率分布，计算效率很高，因此在对计算速度要求较高并且需要掌握输出随机变量准确概率分布时，半不变量法更为实用。

半不变量法通常采用线性化交流模型，负荷的波动以及风电出力的随机性会使节点注入功率远离基准值，使得线性化处理引起较大误差[6]。风电出力波动范围较大，大规模风电并网可能导致输出随机变量的三阶或四阶距也较大，使得采用A型Gram-Charlier级数或Edgeworth级数拟合的概率密度函数出现负值，导致方法失效[7]。针对线性化模型引起较大误差以及概率密度出现负值的问题，文献[7]提出采用分段线性化手段减小潮流方程线性化误差，并引入C型Gram-Charlier级数避免了所拟合的概率密度函数出现负值的情况。为了解决级数法得到负值概率密度以及存在截断误差的问题，文献[8]基于累积量框架采用最大熵模型求解概率潮流。文献[9]将风电出力离散化并对多个风电场出力进行组合，得到多个出力组合状态及相应的概率，基于全概率公式整合每个出力组合状态下的概率潮流结果得到最终的概率潮流。该方法不采用级数方法或最大熵模型拟合分布函数，而通过整合多个Gauss函数拟合分布，相当于在多个运行点线性化潮流方程，因此具有很高的精度，并且计算过程简单直观。

上述概率潮流计算方法最初都是假定输入随机变量之间是相互独立的[10]，而实际上同一地区的负荷可能同时增大或减少，邻近的多个风电场风速具有较强相关性[11]，因此有必要在原始方法的基础上加入能处理相关性的技术手段。概率潮流中常用处理随机变量相关性的方法有Cholesky分解[12]、Rosenblatt变换[13]、Nataf变换[14]和多项式正态变换[15]，但半不变量法一般只采用Choleky分解处理随机变量的相关性，主要由于其他方法属于非线性变换，在半不变量法中不适用。为处理非正态分布随机变量的相关性和提高计算速度，文献[16]提出采用Rackwitz-Fiessler变换将Nataf变换线性化，将改进的Nataf变换法应用于半不变量法，取得了较好的效果，但线性化过程较复杂且存在线性化误差。

为有效处理风电出力波动范围较大导致传统半不变量法失效的问题，本文借鉴文献[9]将风电出力不确定性与负荷不确定性分开进行处理的思想，针对其没有考虑输入变量相关性的不足，提出一种可考虑输入变量相关性的基于拟蒙特卡洛的半不变量法(cumulant method based on quasi Monte Carlo，CM-QMC)计算概率潮流。该方法采用基于Nataf变换的拟蒙特卡洛法(Nataf transformation based quasi Monte Carlo，NQMC)产生具有相关性的风电出力样本，采用基于Cholesky分解的半不变量法来计算各风电出力样本下的概率潮流，通过整合各样本下的概率分布得到最终的电力系统概率潮流结果。在含多个风电场的IEEE 30节点系统上进行仿真，结果表明对于仅考虑风电和负荷不确定的概率潮流，所提出的方法具有很高的精度，并且计算效率远高于蒙特卡洛模拟法。

1 风电出力样本生成

1.1 风电场概率模型

采用应用较广的双参数Weibull分布作为风电场风速概率模型，其概率密度函数为

(1)

式中：v为风速；k、c分别为Weibull分布的形状参数和尺度参数。

风电机组输出功率用下式近似描述：

(2)

式中：vin、vr和vout分别为风机的切入风速、额定风速及切出风速；Pr为风机额定输出功率；Pw为风机实际输出功率。

为简化计算，本文假设风电场装设的风电机组型号相同，风电场以恒定功率因数控制方式并网运行。

1.2 基于Nataf变换的拟蒙特卡洛法

文献[17]通过仿真实验指出，在相同采样规模下，拟蒙特卡洛法计算效率高于基于拉丁超立方抽样的蒙特卡洛法。因此，为提高采样效率，本文采用NQMC方法生成具有相关性的风电出力样本。

1.2.1Nataf变换

设X=[x1,x2,…,xm]是m维服从任意分布的随机向量，随机变量xi的累计分布函数为Fi(xi)。标准正态随机向量Y=[y1,y2,…,ym]可由下式得到：

yi=Φ-1[Fi(xi)]

(3)

式中Φ-1[·]为标准正态分布的逆累计分布函数。

设ρX=(ρXij)m×m、ρY=(ρYij)m×m分别为随机向量X和Y的线性相关系数矩阵，矩阵中各元素的关系满足下式：

(4)

式中：μi、σi、μj和σj分别为随机变量xi与xj的期望和标准差；φ2(yi,yj,ρYij)为yi和yj的联合概率密度函数。文献[18]提供了计算ρYij的半经验公式，本文采用这一方法。上述步骤完成了服从任意分布的随机向量到相关的标准正态随机向量的变换，若能够得到随机向量Y的样本，则通过变换X=F-1[Φ(Y)]可得到随机向量X的样本。下面介绍如何得到相关系数矩阵为ρY的标准正态分布样本。

设Z=[z1,z2,…,zm]为m维相互独立的标准正态分布随机向量。对ρY进行Cholesky分解得到下三角矩阵L，则有Y=LZ。可以看出，若要得到相关系数矩阵为ρY的标准正态分布样本，则需先得到相互独立的标准正态分布样本。首先对标准正态分布进行采样得到样本矩阵，再通过排序方法可得到相关系数矩阵趋于单位矩阵的标准正态分布样本矩阵。排序方法有多种，本文采用Cholesky分解法[19]进行排序。

1.2.2拟蒙特卡洛法

拟蒙特卡洛法利用低偏差序列进行采样，使得采样得到的样本能均匀地填充采样空间。常用的低偏差序列有Halton序列、Faure序列以及Sobol序列，本文采用Sobol序列，其生成的步骤简述如下。

(1)选取本原多项式pi(x)如下：

pi(x)=xsj+a1,jxsj-1+…+asj-1,jx+1，j=1,2,…,m

(5)

式中：m为Sobol序列的维数；a1,j,…asj-1, j∈{0,1}为第j维本原多项式的系数；sj为第j维本原多项式的幂。

(2)选取正整数序列初始值m1,j,m2,j,…,msj,j，需保证mk,j(1≤k≤sj)为奇数且小于2k。对于kgt;sj，有递归公式：

mk,j=2a1,jmk-1,j⊕22a2,jmk-2,j⊕…⊕

2sjmk-sj,j⊕mk-sj,j

(6)

式中⊕为按位异或算子。

(3)计算方向数vk,j：

vk,j=mk,j/2k

(7)

Sobol序列的第j维第i个采样值由下式计算：

xi,j=b1v1,j⊕b2v2,j⊕…⊕bkvk,j⊕…

(8)

式中bk是第i个采样值的二进制(…b2b1)2的右数第k位。

由上述步骤可看出，当本原多项式及正整数序列初始值确定，Sobol序列可根据式(6)至式(8)计算得到。文献[20]已给出多达1 111维的本原多项式及正整数序列初始值，本文加以利用得到Sobol序列。

1.2.3基于Nataf变换的拟蒙特卡洛法

1.2.1节提供了从相互独立的标准正态分布样本到服从任意分布的随机向量样本的变换方法，而1.2.2节提供了拟蒙特卡洛采样方法。文献[21]提出了能够处理相关性的拉丁超立方采样方法，以此为基础，本文提出计及相关性的拟蒙特卡洛方法，其流程如下：

(1)对m个标准正态分布进行n次拟蒙特卡洛采样，得到样本矩阵Wm×n，对Wm×n进行基于Cholesky分解法的排序，得到相关系数矩阵趋于单位矩阵的标准正态分布样本矩阵Zm×n。

(2)由随机向量X的分布和相关系数矩阵ρX得到随机向量Y的相关系数矩阵ρY，对其进行Cholesky分解得到下三角矩阵L。由Y=LZ得到相关系数矩阵为ρY的标准正态分布样本矩阵Ym×n，由Ym×n得到其顺序矩阵Ls。

(3)对随机向量X进行拟蒙特卡洛采样，按顺序矩阵排序得到最终的样本矩阵Sm×n。

2 半不变量法计算概率潮流

2.1 潮流方程线性化模型

将极坐标形式的交流潮流方程在基准运行点处进行泰勒展开，忽略2次及以上的高次项，可得到：

(9)

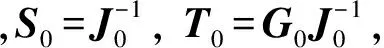
2.2 输入随机变量相关性处理

先假设节点注入功率变量相互独立，利用半不变量法的齐次和可加性可得：

(10)

当计及节点注入功率变量的相关性时，处理方法是将相关随机变量表示为不相关随机变量的线性组合。通常认为发电机注入功率变量之间相互独立，负荷注入功率变量具有相关性。设负荷注入功率向量协方差矩阵为Cw，可由相关系数矩阵及向量标准差计算得到。对Cw进行Cholesky分解得到下三角矩阵G，则有：

(11)

对式(10)进行修正可得：

(12)

求得ΔX、ΔZ的各阶半不变量，可通过级数展开或最大熵原理得到扰动部分的概率分布，将其右移X0、Z0，便得到节点状态向量及支路潮流向量的概率分布。

3 负荷正态分布时的概率潮流

3.1 正态分布特性

本文仅考虑风电及负荷的不确定性，且设负荷注入功率向量服从多维正态分布，当采用风电出力样本描述风电随机性时，系统不确定量仅为服从多维正态分布的负荷注入功率向量WL。当采用2.1节线性化模型后，根据正态变量线性变换不变性定理可知，各风电出力样本下的状态变量服从正态分布，因此仅需计算其期望和方差。

3.2 状态变量的概率分布计算

各风电出力样本下，负荷注入功率取期望值，则进行确定性潮流计算得到X0、Z0，其为节点状态向量X及支路潮流向量Z期望值的近似值[22]，且近似值的误差与方差有关。本文将X0、Z0作为各样本下X、Z的期望值，忽略了较小的误差。

以节点状态向量X为例，说明前2阶原点距和半不变量的关系。

(13)

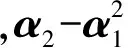
由上述方法可计算得到各风电出力样本下状态变量的期望与方差，根据其正态分布特性便可得到该状态变量的概率分布，其累计分布函数如式(14)。根据全概率公式，对各样本下状态变量的概率分布进行加权，由式(15)计算得到状态变量最终的累计分布函数和概率密度函数。

(14)

(15)

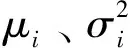
3.3 计算流程

本文所提方法流程如图1所示，主要由3部分组成：风电出力样本的产生、计及相关性的半不变量法概率潮流以及状态变量的概率分布计算。

图1 CM-QMC算法流程Fig.1 Flow chart of CM-QMC method

4 算例分析

4.1 算例说明

本文采用IEEE 30节点系统验证所提方法。将2个风电场接入节点10，每个风电场各包含20台1.5 MW风电机组，其切入风速、额定风速、切出风速分别为3.5、13、25 m/s。风电场风速Weibull分布的形状参数k=2.11，尺度参数c=9，两风电场风速之间的相关系数为0.9。风电场以恒定功率因数控制方式并网运行，且功率因数为0.98，从电网吸收部分无功功率。

各节点负荷期望值为测试系统负荷确定值，标准差为期望值的10%，负荷有功与无功功率不相关。将系统分为2个区域，节点1—15为区域1，节点16—30为区域2，区域内负荷的相关系数为0.9，区域间负荷的相关系数为0.5。

将本文方法与基于Nataf变换的简单随机采样(Nataf transformation based simple random sampling，NSRS)蒙特卡洛法、NQMC进行比较，以50 000次NSRS方法得到的概率潮流结果作为准确值。为了全面验证本文所提方法的有效性，引入相对误差、方差和的根均值[23](average root mean square，ARMS)2项指标。

(16)

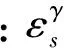
(17)

4.2 性能评估

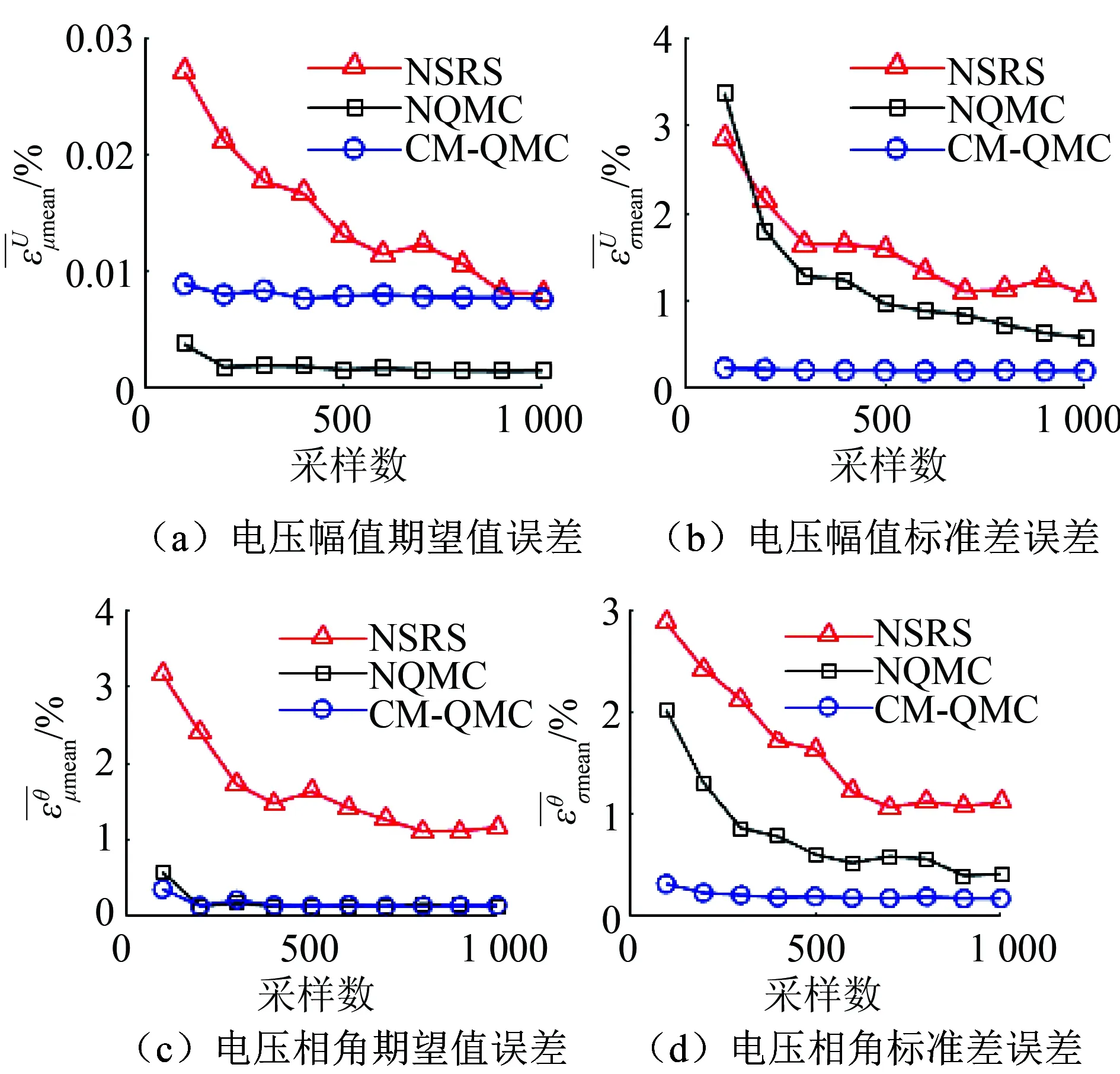
图2 电压幅值相位误差曲线Fig.2 Error curves of bus voltage magnitude and phase

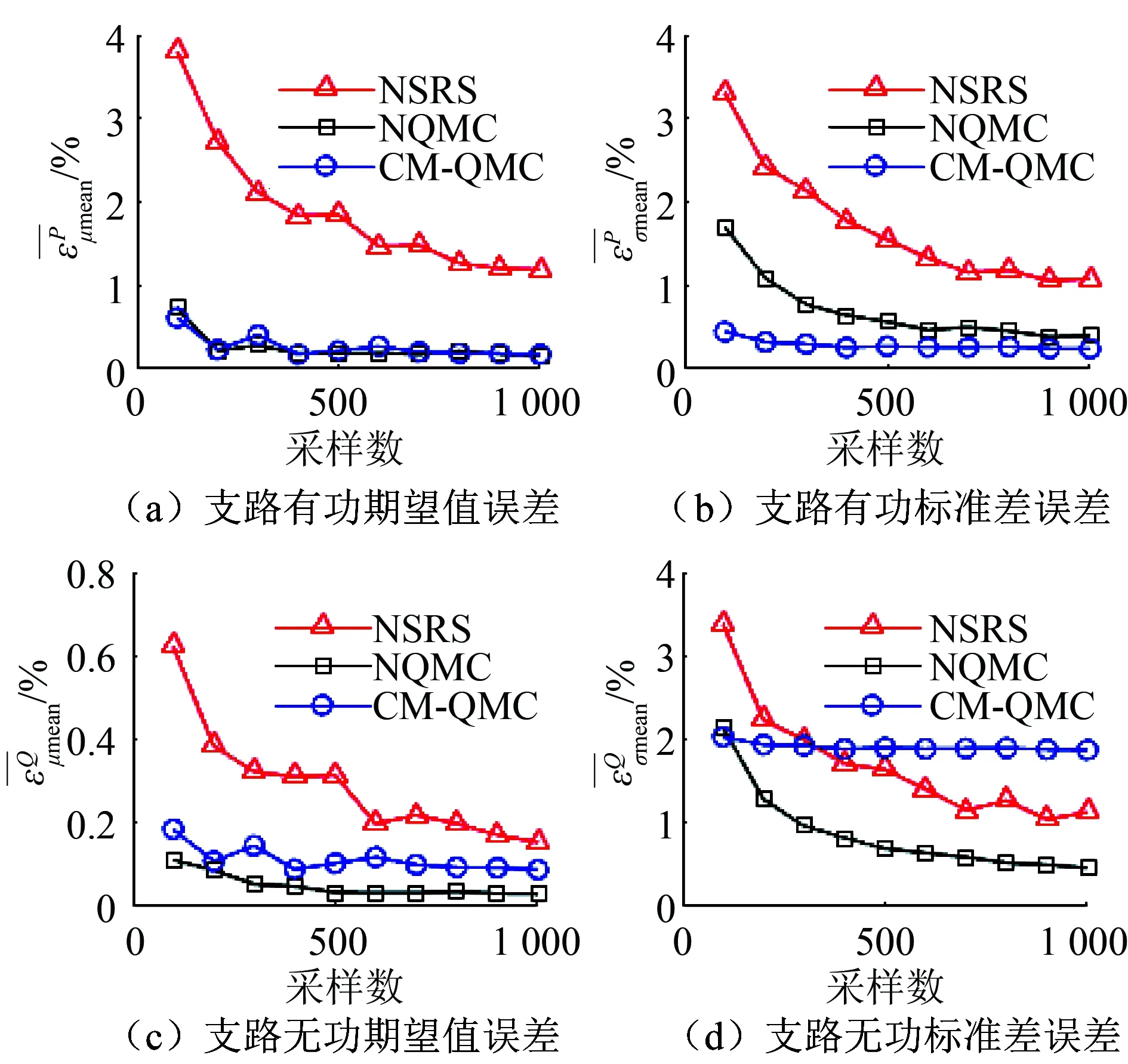
图3 支路潮流误差曲线Fig.3 Error curves of branch power flow

选取节点10(风电场接入节点)电压幅值为考察对象，100次采样的3种方法和50 000次采样的NSRS方法得到的概率密度函数如图5所示。从图中可知，采样规模为100次的CM-QMC得到的概率分布拟合精度高于其他2种方法，主要由于CM-QMC采用多个正态分布进行拟合，而NSRS和NQMC采用核密度估计等方法进行拟合。当采样规模小时，核密度估计等方法的误差较大。

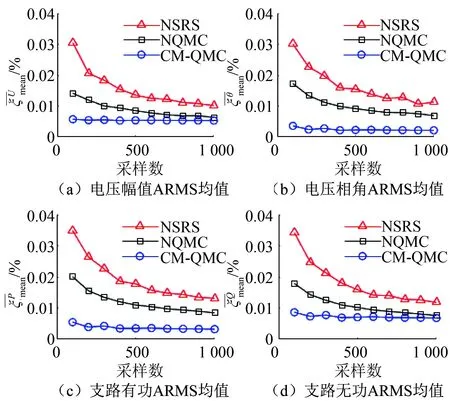
图4 输出变量ARMS均值Fig.4 Average ARMS of output variables

图5 节点10电压幅值概率密度函数Fig.5 Probability density function of bus10 voltage magnitude

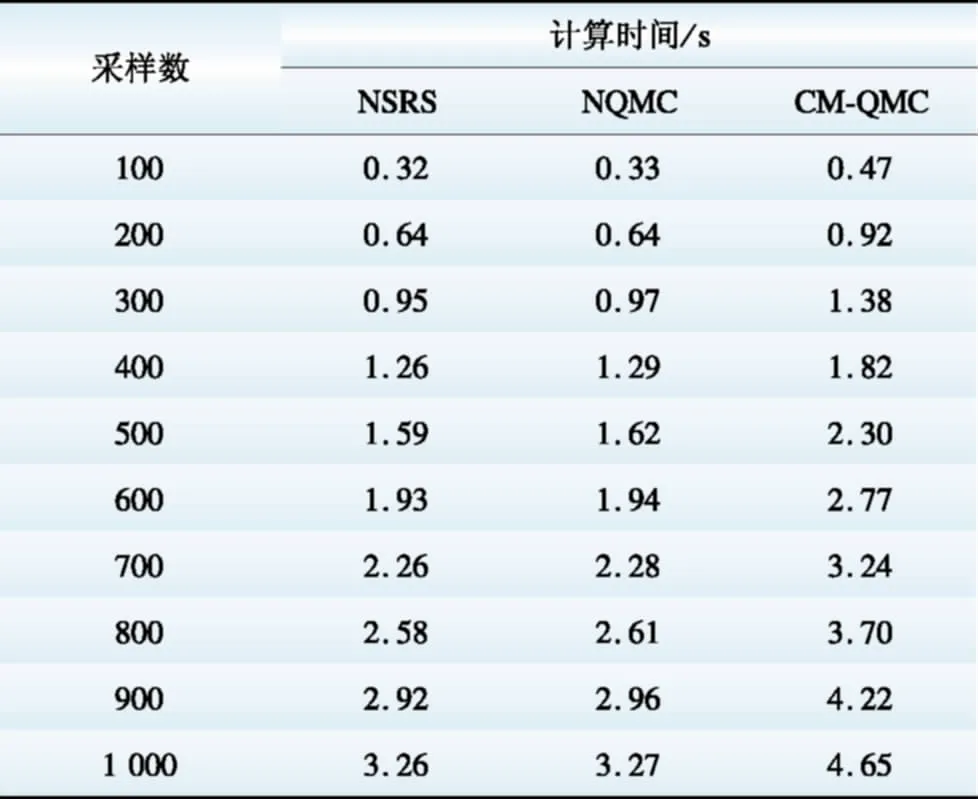
在CPU为Intel Core i5-6500 3.2G Hz、内存为 4 GB的计算机上，采用Matlab R2017a软件编程进行仿真计算。定义计算时间为随机变量样本的产生、确定性潮流计算(半不变量法概率潮流计算)，不进行计算结果的统计分析。不同采样规模下3种方法计算时间如表1所示。从表中可以看出，在相同采样规模下NSRS和NQMC计算时间相近，说明通过拟蒙特卡洛法产生样本消耗很少的时间。CM-QMC需要计算输出随机变量的2阶半不变量，因此消耗的时间高于另2种算法，但CM-QMC的优势在于算法收敛速度快、拟合曲线精度高，在达到相同的计算精度时，所需采样数较少，计算时间会更短。

表13种方法计算时间比较
Table1Computationaltimecomparisonofthreemethods

5 结 论

针对概率潮流算法中模拟法耗时过长、半不变量法线性化模型引起误差较大以及概率密度出现负值等不足，本文将拟蒙特卡洛法与半不变量法相结合，提出一种考虑输入变量相关性的CM-QMC算法。

与传统半不变量法相比，本文方法虽然需要进行多次半不变量计算，但只需计算2阶半不变量，通过整合多个正态分布得到状态变量的概率分布，避免了概率密度出现负值的情况。并且采用拟蒙特卡洛法产生风电出力样本，相当于在各样本点处线性化潮流方程，减小了线性化模型引起的误差。算例结果表明，本文方法在较小采样规模下即可得到状态变量精确的数字特征和概率分布，因此与模拟法通常需要较大采样规模相比，本文方法具有更高的计算效率。

[1] BORKOWSKA B．Probabilistic load flow [J]．IEEE Transactions on Power Apparatus and System，1974，93(3)：752-759．

[2] 刘宇，高山，杨胜春，等．电力系统概率潮流算法综述[J]．电力系统自动化，2014，(38)23：127-135．

LIU Yu，GAO Shan，YANG Shengchun，et al．Review on algorithms for probabilistic load flow in power system[J]．Automation of Electric Power Systems，2014，38(23)：127-135．

[3] 丁明，王京景，李生虎．基于扩展拉丁超立方采样的电力系统概率潮流计算[J]．中国电机工程学报，2013，33(4)：163-170．

DING Ming，WANG Jingjing，LI Shenghu．Probabilistic load flow evaluation with extended Latin hypercube sampling [J]．Proceedings of the CSEE，2013， 33(4)：163-170．

[4] 张立波，程浩忠，曾平良，等．基于Nataf逆变换的概率潮流三点估计法[J]．电工技术学报，2016，31(6)：187-194．

ZHANG Libo，CHENG Haohong，ZENG Pingliang，et al．A three-point estimate method for solving probabilistic load flow based on inverse Nataf transformation[J]．Transactions of China Electrotechnical Society，31(6)：187-194．

[5] 黄煜，徐青山，卞海红，等．基于拉丁超立方采样技术的半不变量法随机潮流计算[J]．电力自动化设备，2016，36(11)：112-119．

HUANG Yu，XU Qingshan，BIAN Haihong，et al．Cumulant method based on Latin hypercube sampling for calculating probabilistic load flow[J]．Electric Power Automation Equipment，2016，36(11)：112-119．

[6] 郭效军，蔡德福．不同级数展开的半不变量法概率潮流计算比较分析[J]．电力自动化设备，2013，33(12)：85-90．

GUO Xiaojun，CAI Defu．Comparison of probabilistic load flow calculation based on cumulant method among different series expansions[J]．Electric Power Automation Equipment，2013，33(12)：85-90．

[7] 朱星阳，刘文霞，张建华．考虑大规模风电并网的电力系统随机潮流[J]．中国电机工程学报，2013，33(7)：77-85．

ZHU Xinyang，LIU Wenxia，ZHANG Jianhua．Probabilistic load flow method considering large-scale wind power integration[J]．Proceedings of the CSEE，2013，33(7)：77-85．

[8] 隋冰彦，侯恺，贾宏杰，等．基于最大熵原理的含风电和电动汽车电力系统概率潮流[J]．电网技术，2016，40(12)：3696-3705．

SUI Bingyan，HOU Kai，JIA Hongjie，et al．Maximum entropy based probability load flow for power system with wind power and electric vehicles[J]．Power System Technology，2016，40(12)：3696-3705．

[9] 高元海，王淳．基于全概率公式的含风电配电系统概率潮流计算[J]．中国电机工程学报，2015，35(2)：327-334．

GAO Yuanhai，WANG Chun．Probabilistic load flow calculation of distribution system including wind farms based on total probability formula[J]．Proceedings of the CSEE，2015，35(2)：327-334．

[10] 杨欢，邹斌．含相关性随机变量的概率潮流三点估计法[J]．电力系统自动化，2012，36(15)：51-56．

YANG Huan，ZHOU Bin．A three-point estimate method for solving probabilistic power flow problems with correlated random variables[J]．Automation of Electric Power Systems，2012，36(15)：51-56．

[11] 石东源，蔡德福，陈金富，等．计及输入变量相关性的半不变量法概率潮流计算[J]．中国电机工程学报，2012，32(28)：104-113．

SHI Dongyuan，CAI Defu，CHEN Jinfu，et al．Probabilistic load flow calculation based on cumulant method considering correlation between input variables[J]．Proceedings of the CSEE，2012，32(28)：104-113．

[12] MORALES J M，BARINGO L，CONEJO A J，et al．Probabilistic power flow with correlated wind sources[J]．IET Generation，Transmission and Distribution，2010，4(5)：641-651．

[13] MOHAMMADI M，SHAYEGANI A，ADAMINEJAD H．A new approach of point estimate method for probabilistic load flow[J]．International Journal of Electrical Power amp; Energy Systems，2013，51(10)：54-60．

[14] 韩海腾，高山，吴晨，等．基于Nataf变换的电网不确定性多点估计法[J]．电力系统自动化，2015，39(7)：28-34．

HAN Haiteng，GAO Shan，WU Chen，et al．Uncertain power flow solved by multi-point estimate method based on Nataf transformation[J]．Automation of Electric Power Systems，2015，39(7)：28-34．

[15] 蔡德福，石东源，陈金富．基于多项式正态变换和拉丁超立方采样的概率潮流计算方法[J]．中国电机工程学报，2013，33(13)：92-100．

CAI Defu，SHI Dongyuan，CHEN Jinfu．Probabilistic load flow calculation method based on polynomial normal transformation and Latin hypercube sampling[J]．Proceedings of the CSEE，2013，33(13)：92-100．

[16] 赵来鑫，赵书强，胡永强．考虑光伏发电相关性的概率潮流计算[J]．华北电力大学学报，2017，44(2)：68-74．

ZHAO Laixin，ZHAO Shuqiang，HU Yongqiang．Probabilistic load flow calculation considering correlativity of photovoltaic generation[J]．Journal of North China Electric Power University，2017，44(2)：68-74．

[17] 方斯顿，程浩忠，徐国栋，等．基于Nataf变换含相关性的扩展准蒙特卡洛随机潮流方法[J]．电工技术学报，2017，32(2)：255-263．

FANG Sidun，CHENG Haozhong，XU Guodong，et al．A Nataf transformation based on extended quasi Monte Carlo simulation method for solving probabilistic load flow problems with correlated random variables [J]．Transactions of China Electrotechnical Society，2017，32(2)：255-263 ．

[18] LIU P L，DER K A．Multivariate distribution models with prescribed marginals and covariances[J]．Probabilistic Engineering Mechanics，1986，1(2)：105-112．

[19] YU H，CHUNG C Y，WONG K P，et al．Probabilistic load flow evaluation with hybrid Latin hypercube sampling and cholesky decomposition[J]．IEEE Transactions on Power Systems，2009，24(2)：661-667．

[20] JOE S，KUO F Y．Remark on algorithm 659：Implementing Sobol’s quasi random sequence generator[J]．ACM Transaction on Mathematical Software，2003，29(1)：49-57．

[21] 陈雁，文劲宇，程时杰．考虑输入变量相关性的概率潮流计算方法[J]．中国电机工程学报，2011，31(22)：80-87．

CHEN Yan，WEN Jinyu，CHENG Shijie．Probabilistic load flow analysis considering dependencies among input random variables[J]．Proceedings of the CSEE，2011，31(22)：80-87．

[22] 刘艳丽．随机潮流中正态变量线性变换不变性定理应用的研究[D]．天津：天津大学，2009．

LIU Yanli．Study on the application of the linear transformation invariance of normal variables in probabilistic load flow[D]．Tianjin：Tianjin University，2009．

[23] ZHANG P，LEE S T．Probabilistic load flow computation using the method of combined cumulants and Gram-Charlier expansion [J]．IEEE Transactions on Power Systems，2004，19(1)：676-682．

2017-06-22

栗然(1965)，女，博士，教授，主要研究方向为新能源与并网技术；

范航(1993)，男，硕士研究生，通讯作者，主要研究方向为电力系统分析、运行与控制；

张凡(1993)，男，硕士研究生，主要研究方向为电力系统分析、运行与控制；

靳保源(1992)，男，硕士研究生，主要研究方向为电力系统分析、运行与控制。

(编辑 张小飞)

QuasiMonteCarloBasedCumulantMethodforProbabilisticLoadFlowCalculation

LI Ran, FAN Hang, ZHANG Fan, JIN Baoyuan

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Baoding 071003, Hebei Province, China)

With the increasing penetration of wind sources, not only the uncertainty of wind power output, but also the correlation of wind power output due to wind speed correlations among adjacent wind farms should be considered in probabilistic load flow (PLF) methods. In allusion to the correlation and large fluctuation range of wind power output, this paper proposes a quasi Monte Carlo (QMC) based cumulant method of PLF considering the correlation between input variables. QMC based on Nataf transformation is used to generate wind power output samples with correlation, and the cumulant method is used to calculate PLF at each sample point. With the state variables satisfying the normal distribution at each sample point, the final probability distributions are obtained by integrating all normal distributions according to the total probability formula. The comparative tests in the IEEE 30-bus system demonstrate that the proposed method has high computational precision under the small sampling size, and can obtain the probability distribution of the system state variables accurately.

probabilistic load flow; cumulant method; quasi Monte Carlo; wind power integration

TM74

A

1000-7229(2017)11-0144-07

10.3969/j.issn.1000-7229.2017.11.019