基于改进二进制蝙蝠算法的独立型微网容量优化配置

盛四清，张晶晶，陈玉良

(新能源电力系统国家重点实验室(华北电力大学), 河北省保定市 071003)

基于改进二进制蝙蝠算法的独立型微网容量优化配置

盛四清，张晶晶，陈玉良

(新能源电力系统国家重点实验室(华北电力大学), 河北省保定市 071003)

该文围绕独立型风/光/柴/储微网的容量优化配置展开研究，以微网系统供电可靠性为约束条件，同时考虑微网经济性、环保性和可再生能源利用率3个指标，以加权后的年均综合费用最小为优化目标，构建微网容量优化配置的非线性整数规划模型。针对连续优化算法直接用于求解离散优化模型而导致的局部最优问题，该文提出一种改进的二进制蝙蝠算法(improved binary bat algorithm, IBBA)，将差分进化(differential evolution, DE)算法的变异、交叉、选择操作与二进制蝙蝠算法(binary bat algorithm, BBA)相结合，增强BBA的全局寻优能力。算例结果表明，IBBA求解得到的配置结果在精度和稳定性上均优于遗传算法(genetic algorithm, GA)、粒子群算法(particle swarm optimization, PSO)和DE算法。

独立型微网; 优化配置; 改进二进制蝙蝠算法(IBBA); 差分进化算法(DE)

0 引 言

独立型微网可将各类分布式电源、储能装置以及负荷有效整合在一起，具有供电灵活、可近距离输电等优点，已成为解决偏远地区(如孤岛、边防哨所等)供电问题的关键技术[1-2]。微网容量优化配置是设计微网的一个重要环节，指的是根据待规划地区风光等自然资源以及负荷特点，通过优化方法确定待规划微网中分布式电源和储能装置的容量，使得整个微网在保障供电可靠性的前提下，提高其经济性和环保性。科学合理的配置方案对于降低微网建设成本、保障供电可靠性、提升可再生能源消纳水平以及减少污染排放具有重要意义[3]。

微网优化配置问题是一个多目标、多约束、具有强非线性的复杂优化问题，传统的数学优化算法往往难以奏效，群体智能算法是解决该类问题最常用的方法。在过去的几年里，很多群体智能算法被应用于微网优化配置的研究[4-12]。文献[4]以综合成本费用最小为优化目标，利用遗传算法(genetic algorithm, GA)对独立风光柴储微网的系统容量进行优化；文献[5]提出一种自适应粒子群算法(particle swarm optimization, PSO)来求解海上油田微电网电源优化配置问题，将变异操作引入到粒子群算法中，以此来改善迭代后期全局搜索能力下降的问题；文献[6]将改进的细菌觅食算法应用于风/光/储混合微网的电源容量优化配置；文献[7]在对海岛微网进行优化配置时考虑海水淡化类可时移负荷的影响，并采用改进的自由搜索算法进行求解；文献[8]选取仿电磁学算法来对风/光/柴/储独立微电网进行优化配置，并采用自适应变异、自适应变步长以及搜索空间缩减等措施来改善算法的性能。

微网优化配置问题本质上是整数规划问题，然而除GA外，上述文献中提到的方法多为连续优化算法，大部分文献采用取整的方式将其直接应用于微网配置问题，这种处理方式往往会使算法陷入局部最优，从而得不到令人满意的配置方案。虽然GA可以通过二进制编码来求解离散优化问题，但是GA同样存在易早熟收敛等缺陷，因此，探索更适合解决微网优化配置问题的优化算法是当前需要解决的一大问题。

蝙蝠算法(bat algorithm, BA)是由剑桥大学的YANG X于2010年提出的一种模仿蝙蝠回声定位行为的群体智能算法，该算法具有全局搜索能力强、收敛速度快等优点，在多个非线性测试函数上的仿真结果表明：相比于GA和PSO，BA能得到更高精度的解且寻优效率更高[13]。然而，BA同样是一种连续性优化算法，需要将其转换成二进制BA才能更好地适用于微网优化配置问题。此外，基本的BA仍然存在早熟收敛、局部搜索能力差等问题，仍需对其加以改进，进一步提高其寻优性能。

本文以风/光/柴/储独立微网为配置对象，在保障微网供电可靠性前提下，同时考虑经济性、环保性以及可再生能源利用率3项指标，将3项指标统一转换为费用，以年均综合费用最小为优化目标，建立起微网容量配置的非线性整数优化模型。提出一种基于差分进化算法的改进二进制蝙蝠算法来求解上述优化模型，并将该算法与传统的智能算法进行对比，最后分析权重系数对配置结果的影响。

1 分布式电源模型

1.1 风力发电机

风力发电机(wind turbine, WT)利用清洁、可再生的风能资源进行发电，风机输出功率Pwt(t)主要受到风速的影响，其数学关系式[4]为：

(1)

(2)

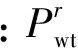
1.2 太阳能光伏电池

太阳能光伏电池(photovoltaic，PV)通过光伏组件、发电装置，将光能转化成电能，其发电量主要受环境温度和光照强度的影响。PV的输出功率Ppv可按式(3)计算得到[4]：

Ppv=PSTCGAC[1+k3(Tc-Tr)]/GSTC

(3)

式中：PSTC为标准测试条件下的最大测试功率；GAC为光照强度，kW/m2；k3为功率温度系数，取k3=-0.34%/K；Tr为参考温度，取Tr=25oC(计算时需要换算到K)；GSTC为标准测试条件下的光照强度，取GSTC=1 kW/m2；Tc为电池板工作温度。

Tc的计算式为

Tc=Tamt+30GAC/1 000

(4)

式中：Tamt为环境温度。

1.3 柴油发电机

柴油发电机(diesel，DIE)是一种小型、可控、以柴油为燃料的电源，其耗油量Foil与其输出功率相关[10]：

(5)

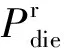
1.4 电池储能系统

蓄电池储能系统(battery energy storage system, BESS)由多组蓄电池组成。电池充放电状态(state of charge, SOC)是衡量蓄电池剩余电量的重要参数，SOC由前一时刻剩余电量和相邻时刻充放电功率决定[7]。

(6)

2 微网优化配置模型

2.1 目标函数

本文以风机台数nwt、光伏电池板个数npv、柴油发电机台数ndie和储能系统中蓄电池个数nbess作为优化变量，在保障系统供电可靠性的前提下，同时优化经济性、环保性以及可再生能源利用率3个优化指标，为统一量纲，将所有指标都转换为费用来处理，最终以年均综合费用最小为优化目标进行微网容量优化配置。下面分别对3项指标进行介绍，其中，可靠性指标将作为约束条件，在2.2节中进行介绍。为描述方便，在本文中将WT、PV、DIE和BESS分别依次定义为第1～4类分布式电源。

2.1.1经济成本指标

经济成本CE共包括4部分：年平均初始投资费用Cinitial、年平均设备运维费用Coperation、替换费用Cchange以及燃料费用Cfuel，可表示为

CE=Cinitial+Coperation+Cchange+Cfuel

(7)

(1)年平均初始投资费用。

(8)

(2) 年平均设备运维费用。

年平均设备运维费用与第1年的运维成本有关，其计算式为

(9)

(3) 替换费用。

年平均替换成本与各类分布式电源的使用寿命有关：

(10)

式中：y为系统的全寿命年限；Li为第i类分布式电源在系统的全寿命年限内的更换次数，由各电源的使用年限可求出各电源更换次数。

(4) 燃料费用。

(11)

式中：koil为柴油发电机燃料费用系数；Pdie(t)为柴油发电机的实际运行功率；T为年运行小时数。

2.1.2环保性指标

柴油机在运行过程中会排放出CO2,SO2,NOx等污染性气体，在本文中依次定义为第1～3类污染物，为方便比较，需将其转化为治污费用。治污费用CP与柴油发电机的输出功率有关，其计算式为

(12)

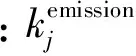
2.1.3可再生能源利用率指标

由于风光资源的随机性，系统在运行过程中会存在弃风、弃光等问题，即微网系统电源出力大于用电需求，导致能量浪费和可再生能源利用率下降。这里引入能量浪费惩罚费用CW来衡量系统可再生能源的利用率：

(13)

式中：kwaste为能量浪费惩罚系数；Pwaste(t)为t时刻功率盈余量。

综合上述3项指标，微网优化配置的目标函数为

minf(x)=w1CE+w2CP+w3CW

(14)

式中：x=[nwt,npv,ndie,nbess]为待优化变量；w1～w3为各目标的权重系数。

2.2 约束条件

2.2.1蓄电池电量和功率约束

蓄电池的寿命与其是否深度放电有关，过充或过放都会减少蓄电池的寿命。为延长蓄电池的使用寿命，需要对蓄电池的充、放电过程进行约束。当蓄电池荷电状态SSOCgt;0.9时，蓄电池停止充电；当SSOClt;0.1时，蓄电池停止放电，且1 h内充、放电电量不能超过额定容量的20%：

(15)

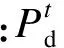
2.2.2功率缺额率约束

系统的可靠性表现为系统功率缺额的大小，过大的功率缺额会对生产和生活造成较大的影响，因此需要对系统的功率缺额进行约束，以保证整个微网系统的供电可靠性。本文将系统的最大缺电率设置为0.1%，即功率缺额量不能超过系统总负荷的0.1%，功率缺额率可按下式计算：

(16)

式中：Pi(t)为第i种分布式电源t时刻的输出功率；Pload(t)为t时刻的负荷；PLoad为微网系统的年总负荷。在模型求解时，可将功率缺额率转换成惩罚项来处理。

3 优化算法

3.1 运行控制策略

微网的运行控制策略决定了各类分布式电源出力的优先次序，其对最后的微网优化配置结果影响较大。本文采用的运行控制策略如图1所示。具体的控制流程总结如下详述。

(1) 当风机及光伏出力之和大于负荷时，由风机和光伏给负荷供电。若此时电池储能系统有可充电容量，则用剩余电量给储能系统充电。当电池储能系统无可充电容量，即不能继续储存剩余电量时，会将其直接丢弃，造成能量浪费。

(2) 当风机及光伏发电量之和小于负荷时，优先由蓄电池储能系统放电来提供功率，如果仍不能满足负荷需求，则启动柴油发电机给负荷供电。当风机、光伏、蓄电池和柴油机联合供电还不满足负荷需求时，微网就会出现功率缺额。

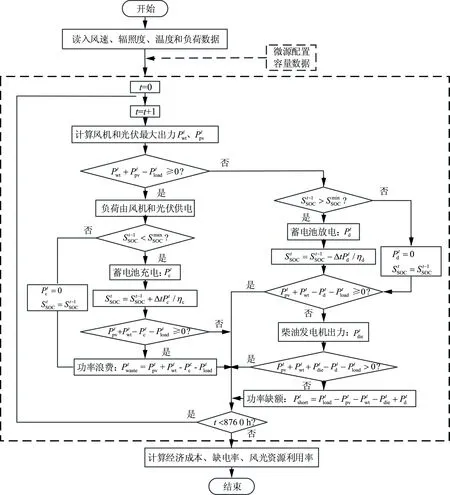
图1 系统运行控制策略流程图Fig.1 Flowchart of control strategy for system operation

3.2 二进制蝙蝠算法

标准BA算法适合用于求解连续性优化问题，而微网优化配置则是一个整数优化问题。若将BA直接用于求解该问题，容易陷入局部最优而得不到令人满意的配置方案。本文通过引入速度转换函数将标准BA转换成二进制BA(binary bat algorithm, BBA)来进行求解，减小算法陷入局部最优的概率。BBA的计算流程如下详述。

步骤3：按照式(17)、(18)更新脉冲频率和个体速度：

(17)

(18)

式中：fmin为最小频率；fmax为最大频率；β是0～1的随机数。

(19)

步骤5：按照下式更新个体m的位置：

(20)

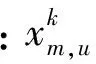
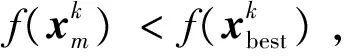
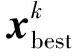
步骤8：重复步骤3～7，直至算法达到最大连续不下降次数或者达到最大迭代次数。

3.3 改进的二进制蝙蝠算法

基本的BBA主要依靠蝙蝠个体之间的信息交换来进行寻优，个体本身缺乏变异机制，一旦受到某个局部极值约束后自身很难摆脱，甚至出现进化停滞的现象。因此需要对基本BBA进行改进，进一步增强其全局寻优能力。

差分进化 (differential evolution, DE) 算法是一种高效的并行优化算法，其优化过程类似于遗传算法，在种群更新时都包含变异、交叉、选择等操作。不同的是，DE具有更加丰富的变异策略，且其变异方式更加有效地利用了种群的分布特性，变异效率更高[14]。因此将DE和BBA算法结合，能克服BA收敛精度不高、易陷入局部最优等缺点。

DE算法不同的变异方式对于算法的全局探索和局部平衡能力各有侧重，本文选取随机向量差分法(DE/rand/1)和最优解加随机向量差分法(DE/best/1)2种变异策略对BBA算法中步骤6得到的蝙蝠个体进行变异操作。值得注意的是，DE算法也是一种连续优化算法，因此本文对其进行相应处理，使其转换成二进制DE。具体操作过程如下详述。

3.3.1变异操作

(1)随机向量差分法(DE/rand/1)。

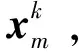
(21)

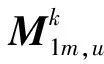
(2)最优解加随机向量差分法(DE/best/1)。

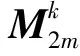
(22)

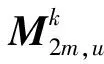
3.3.2交叉操作

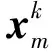
(23)

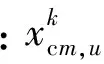
3.3.3选择操作

4 仿真算例

4.1 仿真数据

本文以某地区1年的气象数据和当地219个用户1年的实际用电数据为基础，采用本文提出的优化配置模型和求解算法进行微网容量优化配置。数据采样间隔为1 h，全年8 760 h的风速、辐照度、环境温度和负荷数据分别如图2所示。

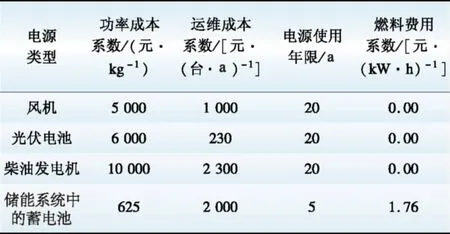
该地区全年总用电量为1 318 MW·h，日平均用电量约为3.6 MW·h。单台风机的额定功率选取为10 kW；单个光伏电池板的额定功率为1 kW；柴油发电机的额定功率为10 kW，其排放污染性气体的标准和治理费用见表1[7]；单个储能电池的额定容量为25 kW·h，额定功率为25 kW；蓄电池的初始剩余电量设为60%的额定电量，充电效率为0.8，放电效率为1。设定系统寿命周期为20年，电源的成本系数和使用年限见表2[10]。

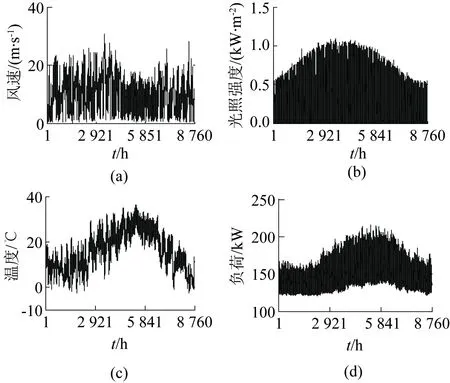
图2 风速、辐照度、温度及负荷曲线Fig.2 Curve of wind speed, irradiance, temperature and load

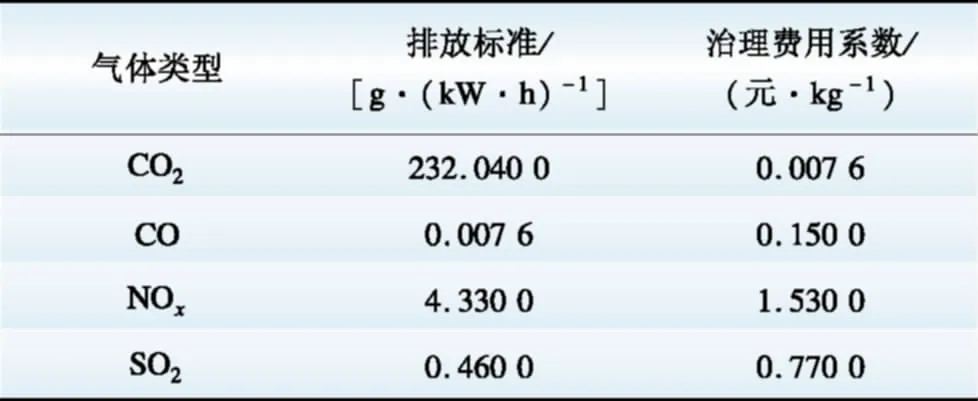
表2 设备参数Table 2 Equipment parameters

4.2 算法对比

为验证本文所提算法的有效性，将本文算法与GA、PSO和DE算法进行对比。4种算法的种群数目都设置成30，目标函数最大连续不下降次数取为20，最大迭代次数取为100，其余参数取值见表3。由于这4种算法都为随机搜索算法，为使对比结果更加可信，分别运行各算法30轮，每一轮都随机产生初始解，且保证4种算法在每轮中的初始解相同。此外，优化模型的权重设置为等权重，最终运行结果见表4,其中1轮的收敛曲线如图3所示。

表34种算法参数取值
Table3Parameterssettingfor4algorithms

表4 4种算法寻优结果对比Table 4 Comparison of optimization resultsamong 4 algorithms

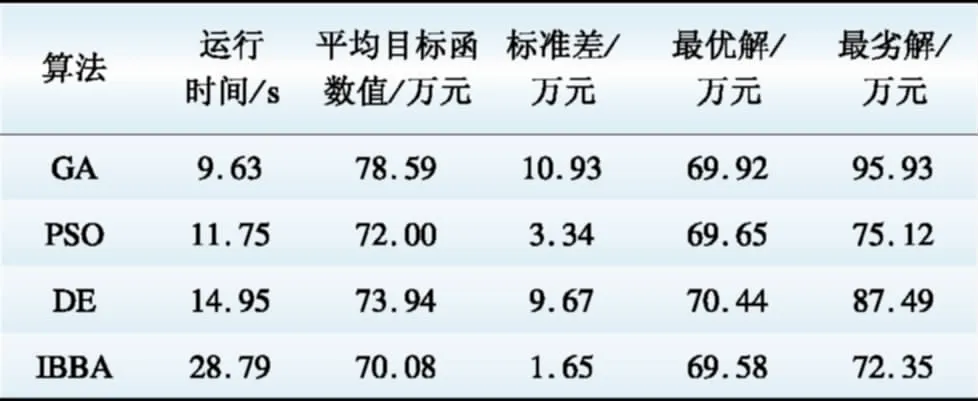
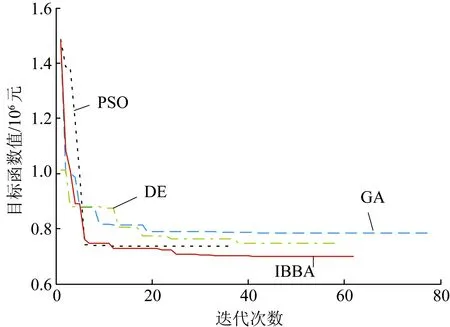
图3 4种算法收敛曲线对比Fig.3 Convergence curve for 4 algorithms

分析表3可知，在种群数和收敛准则相同的前提下，就求解精度而言，IBBA求得的最优解精度最高，平均值为70.08万元，最优值为69.74万元，最差值为72.35万元，PSO和DE次之，GA优化的结果最差。就结果的稳定性而言，IBBA的稳定性最好，其30次运行的标准差为1.65万元，PSO次之，DE更差，GA的稳定性最差。就运行速度而言，GA的运行速度最快，PSO次之，DE比PSO运行速度更慢，IBBA的运行速度最慢，这是因为IBBA在标准的BBA的基础上加入了DE算法，因此运行时间有所增加。考虑到微网优化配置并不是实时在线的，对于算法的运行速度要求并不高，因此综合上述3项指标来看，本文所提出的IBBA算法对微网容量配置问题的求解效果优于GA、PSO和DE这3种传统智能算法。

4.3 目标函数权重对配置结果的影响分析

目标函数权重系数表示决策者对于各个目标的重视程度，为了探究不同权重系数对优化配置的影响，本文分析不同权重系数下容量配置结果的差异。共设置4组权重，以等权重为对照基准，其余3组权重分别对3个目标函数有不同侧重。用IBBA求解，每组权重系数下算法运行30次，取目标函数最小的一次作为最终配置结果，结果见表5。

总体而言，不同的权重设置方案对最终的配置结果影响并不大，等权重设置得到的配置结果年均综合费用最少。与等权重设置相比，年均综合费用最大的配置方案比其大1.6%左右。年均综合费用由经济成本CE、治污费用CP以及能源未利用惩罚费用CW3部分构成。与等权重设置相比，当给CE赋较大权重时，风机光伏的配置容量有所上升，蓄电池配置容量下降，此时经济成本有所下降，但同时可再生能源利用率也有所下降；当给CP赋较大权重时，治污费用并没有出现较大改变，这是因为治污费用占综合费用的比例很小，大约只占0.4%；当给CW赋较大权重时，为提升可再生能源利用率，就需要减少风、光等不确定性电源的配置容量，同时为保证系统可靠性，作为后备电源的柴油机的容量就需要增加，由表5可知，风机光伏的配置容量明显下降，柴油机的配置容量上升，风、光资源利用率增加10%。

表5不同权重系数下的配置结果
Table5Configurationresultsfordifferentweightcoefficients

5 结 论

本文围绕微网容量优化配置问题展开研究，以微网供电可靠性为约束，建立了同时考虑经济性、环保性以及可再生能源利用率3项指标的优化模型，将3项指标转化为经济指标，进而将多目标优化问题转化为单目标问题进行求解，并提出一种改进的二进制蝙蝠算法进行求解，得到的结论如下。

(1)微网容量优化配置问题是一个整数规划问题，采用本文提出的改进二进制蝙蝠算法在求解精度和稳定性方面均优于遗传算法、粒子群算法和差分进化算法等传统优化算法。

(2)目标函数的权重系数会对配置结果产生一定的影响，等权重设置得到的配置方案能够较好地平衡各个目标函数之间的关系，得到的年均综合费用最优。

[1] 王成山，焦冰琦，郭力，等. 微电网规划设计方法综述[J]. 电力建设，2015,36(1):38-45.

WANG Chengshan, JIAO Bingqi, GUO Li, et al. Review of methods of planning and design of microgrids[J]. Electric Power Construction, 2015,36(1):38-45.

[2] 王守相，王慧，蔡声霞. 分布式发电优化配置研究综述[J]. 电力系统自动化，2009,33(18):110-115.

WANG Shouxiang, WANG Hui, CAI Shengxia. A review of optimization allocation of distributed generations embedded in power grid[J]. Automation of Electric Power Systems, 2009,33(18):110-115.

[3] 宋璇坤，韩柳，鞠黄培，等． 中国智能电网技术发展实践综述[J]．电力建设，2016，37(7):1-11．

SONG Xuankun， HAN Liu， JU Huangpei， et al． A review on development practice of smart grid technology in China[J]． Electric Power Construction，2016，37(7):1-11.

[4] 丁明，王波，赵波，等. 独立风光柴储微网系统容量优化配置[J]. 电网技术，2013,37(3):575-581.

DING Ming, WANG Bo, ZHAO Bo, et al. Configuration optimization of capacity of standalone PV-wind-diesel-battery hybrid microgrid[J]. Power System Technology, 2013,37(3):575-581.

[5] 卢锦玲，程晓悦，徐超，等．考虑低碳经济的独立运行微电网系统电源优化配置[J]．华北电力大学学报(自然科学版)，2014，41 (4):61-68．

LU Jinling, CHENG Xiaoyue, XU Chao, et al. Optimal sitting and sizing of distributed generation planning in a standalone micro-grid considering low-carbon economy[J]. Journal of North China Electric Power University(Natural Science Edition)，2014，41(4):61-68．

[6] 马溪原，吴耀文，方华亮，等. 采用改进细菌觅食算法的风/光/储混合微电网电源优化配置[J]. 中国电机工程学报，2011,31(25):17-25.

MA Xiyuan, WU Yaowen, FANG Hualiang， et al．Optimal sizing of hybrid solar-wind distributed generation in an islanded microgrid using improved bacterial foraging algorithm[J]． Proceedings of the CSEE,2011,31(25):17-25．

[7] 刘柏良. 多源微网典型应用的优化设计[D].南京：东南大学，2015.

LIU Bailiang．Design and optimization on microgrid with multi-source in multiple scenarios[D]. Nanjing: Southeast University, 2015．

[8] 谭颖，吕智林，李捷. 基于改进ELM的风/光/柴/储独立微网分布式电源多目标容量优化配置[J]. 电力系统保护与控制，2016,44(8):63-70.

TAN Ying, LUE Zhilin, LI Jie. Multi-objective optimal sizing method for distributed power of wind-solar-diesel-battery independent microgrid based on improved electromagnetism-like mechanism[J]. Power System Protection and Control, 2016, 44(8):63-70.

[9] YANG H，ZHOU W，LU L，et al．Optimal sizing method for stand-alone hybrid solar-wind system with LPSP technology by using genetic algorithm[J]．Solar Energy，2008，82(4)：354-367．

[10] 郭力，刘文建，焦冰琦，等.独立微网系统的多目标优化规划设计方法[J].中国电机工程学报，2014,34(4):524-536.

GUO Li, LIU Wenjian, JIAO Bingqi, et al. Multi-objective optimal planning design method for stand-alone microgrid system[J]. Proceedings of the CSEE, 2014,34(4):524-536.

[11] 牛东晓，马天男，黄雅莉，等.基于Godlike 算法的海岛型分布式电源规划模型[J]. 电力建设，2016,37(9):132-139.

NIU Dongxiao, MA Tiannan, HUANG Yali, et al. Sea-island distributed generation planning model based on godlike algorithm[J]. Electric Power Construction, 2016,37(9): 132-139.

[12] 黎嘉明，郑雪阳，艾小猛，等． 独立海岛微网分布式电源容量优化设计[J].电工技术学报，2016,31(10) : 176-184．

LI Jiaming， ZHENG Xueyang， AI Xiaomeng， et al. Optimal design of capacity of distributed generation in island standalone microgrid[J]. Transactions of China Electrotechnical Society, 2016,31(10):176-184．

[13] YANG X. A new metaheuristic bat-inspired algorithm[C]// 2010 Nature Inspired Cooperative Strategies for Optimization. Berlin: Springer,2010:65-74.

[14] 孔祥勇，高立群，欧阳海滨，等. 无参数变异的二进制差分进化算法[J]. 东北大学学报(自然科学版)，2014,35(4):484-488.

KONG Xiangyong, GAO Liqun, OUYANG Haibin, et al. Binary differential evolution algorithm based on parameter less mutation strategy[J]. Journal of Northeastern University(Natural Science), 2014,35(4):484-488.

2017-05-11

盛四清(1965) ，男，教授，主要研究方向为电力系统运行、 分析与控制；

张晶晶(1991)，女，通信作者，硕士研究生，主要研究方向为微电网规划与运行；

陈玉良(1993)，男，硕士研究生，主要研究方向为电力系统分析与控制。

(编辑 郭文瑞)

OptimalSizingforStand-AloneMicrogridBasedonImprovedBinaryBatAlgorithm

SHENG Siqing, ZHANG Jingjing, CHEN Yuliang

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Source (North China Electric Power University), Baoding 071003, Hebei Province, China)

This paper focuses on the optimal sizing for stand-alone wind-PV-diesel-battery microgrid. Using the reliability of power supply as the constraint condition and the minimum average annual cost after weighting as the objective function, this paper constructs a non-linear integer programming model for the optimal sizing of microgrid which takes economy, environmental protection and renewable energy utilization of microgrid into consideration. Aiming at the local optimal problem caused by directly applying continuous optimization algorithm into solving discrete optimization model, this paper proposes an improved binary bat algorithm (IBBA), which adopts mutation, crossover and selection operations from differential evolution (DE) to improve the global searching ability of standard BBA. The results of a case study indicate that IBBA shows better performance in terms of both the solution quality and stability compared with genetic algorithm (GA), particle swarm optimization (PSO) and DE algorithm.

stand-alone microgrid; optimal allocation; improved binary bat algorithm(IBBA); differential evolution(DE) algorithm

TM72

A

1000-7229(2017)11-0121-08

10.3969/j.issn.1000-7229.2017.11.016