考虑“风-光-荷-储”联合运行的配电网双层规划方法

刘源，杨军，杨丙权，朱旭，陈艳，王宣

(1.武汉大学电气工程学院，武汉市 430072；2. 国网湖北省电力公司武汉供电公司，武汉市 430013)

考虑“风-光-荷-储”联合运行的配电网双层规划方法

刘源1，杨军1，杨丙权2，朱旭1，陈艳2，王宣2

(1.武汉大学电气工程学院，武汉市 430072；2. 国网湖北省电力公司武汉供电公司，武汉市 430013)

分布式电源与储能系统在配电网中的应用是当前研究的热点。提出了一种风机、光伏电源、储能系统在配电网中的双层规划模型。上层模型以投资、运维费用为优化目标，同时考虑区域的购电费用及网损费用，完成风机和光伏电源的容量配置；下层模型提出了一种储能系统削峰填谷的运行策略，基于该策略完成储能系统的选址定容工作。针对以上模型，提出以下求解方法：基于遗传算法求解上层模型，并通过K均值聚类方法对比研究输入数据序列长度对规划结果的影响，通过帕累托分析研究了投资运维费用与购电费用及网损费用的关系；使用YALMIP工具箱完成储能系统运行策略的求解，进而完成储能系统的选址定容工作。最后，通过IEEE-33节点标准配电系统仿真验证了所提模型在风机和光伏电源以及储能系统规划方面的有效性，结果显示所提储能运行策略具有良好的削峰填谷效果。

风机(WT)；光伏电源(PV)；储能系统(ESS)；双层优化；遗传算法；K均值聚类

0 引 言

随着能源危机意识的增强，新能源发电技术的研究与应用得到越来越多的关注[1]。分布式电源由于其环境友好、能够改善能源上网结构等优势，被认为是未来配电网的重要组成部分[2]。分布式电源的接入为配电网侧提供了更多的可利用资源，但光伏、风机等分布式电源受气象因素影响严重，具有波动性和随机性等特点，大大制约了分布式电源上网规模与能源利用率[3-4]。而储能技术的发展，改变了电能即发即用、不能大规模存储的特点，在削峰填谷平抑功率波动、提高供电可靠性等方面发挥了重要作用[5-6]。传统的配电网规划方法主要涉及主站和网架的容量配置问题，分布式电源、储能系统的容量配置对电网规划提出了新的挑战。合理配置分布式电源及储能容量，对新形势下配电网规划具有重要意义。

目前，分布式电源与储能系统的研究在电力系统规划、能量管理和需求侧管理方面[7-11]均已取得了较为丰硕的成果。其中，在配电网系统规划方面：文献[12]提出一种考虑配电公司、分布式电源运营商和用户侧利益的三层规划模型，通过分析各层之间的关系，协调“源-网-荷”三方利益，最终完成电网的拓展规划；文献[13]在传统有源配电网规划模型的基础上，引入需求侧响应费用和电网运行可靠性约束，为含分布式电源的有源配电网规划提供了方法参考。由于分布式电源具有随机性和波动性，单纯的分布式电源接入将严重影响电网的安全稳定运行，同时分布式电源的大规模消纳也难以实现。针对这一问题，一些学者开展了储能系统与分布式电源的联合规划。文献[14]以适应分布式电源和负荷不确定性为基础，将规划问题拆分为运行层和投资层，完成了变电站、馈线、储能系统和无功补偿装置的投资决策。以上文献虽已注意到分布式电源与储能系统联合规划以适应分布式电源的随机性，但在规划阶段未提出考虑储能系统削峰填谷能力的储能配置方法。文献[15]上层以电池储能系统(battery energy storage system，BESS)综合经济效益最大化为规划目标，BESS的配置容量为变量；下层通过启发式方法制定出比较符合实际情况的BESS充放电策略，建立双层规划模型进行求解。文献[16]外层以电网成本最低为目标, 通过遗传算法优化储能配置, 并对遗传算法加以改进, 提高计算效率；内层以降低网损、提高削峰填谷收益为目标，利用序列二次规划算法同时计算多时段配电网最优潮流，实现储能充放电优化。以上文献虽在规划方法中注意到了储能系统的削峰填谷能力，但均根据分时电价制定储能系统的运行策略，在无峰谷电价区域所提规划方法则无法适用，且规划对象单一，缺乏风机、光伏等多类型分布式电源与储能系统的联合规划手段。

此外，当前含分布式电源的配电网规划问题的投资决策变量多属于整数变量的范畴，如DG安装台数，而潮流平衡的考虑则引入了节点电压、功角等连续变量，系统非线性、多变量的实质是一个复杂的非凸优化问题。如果在此基础上进一步考虑储能系统的安装容量及充放电功率，由于储能系统在剩余电量与充放电功率之间存在耦合关系，增加了问题的复杂性。此外，由于非凸优化问题数学工具的局限性，目前多类型分布式电源与储能系统的统一建模、统一求解方法尚未成熟完备，因此，近年来规划模型的求解集中于多阶段分层求解以及智能算法的使用[12,14,17]。已有分层策略单纯以配电网参与对象或规划阶段进行划分，比如以配电网运营商和分布式电源运营商进行划分，或者以投资层和运行层进行划分，这些分层方法未能综合考虑所有决策变量的特点及耦合关系。在涉及风机、光伏、储能系统的多类型分布式电源规划研究中，从这几个规划主体所含决策变量之间耦合关系出发的分层方法仍十分匮乏。根据数学模型相似性进行分层能够剔除耦合变量，避免层与层之间的反复迭代，简化求解过程。另一方面，使用智能算法优势在于求解思路清晰简单，避免了数值解析方法在非线性问题上复杂的松弛与线性变化处理，以及在数据量较大的情况下数值解析方法产生“维数灾”的问题。

基于以上已有研究工作的分析，本文基于模型中变量的相似性及耦合关系划分建立“风-光-荷-储”联合运行的配电网双层规划模型，在上层模型完成风机和光伏电源的定容工作，下层模型提出一种储能系统削峰填谷运行策略，并基于该策略完成储能系统选址定容的经济性计算；针对模型随着时间序列的延长，求解速度降低的问题，本文提出一种基于K均值聚类算法和遗传算法的混合求解策略，并与原始序列的求解结果进行对比分析，分析其在缩减模型求解时间方面的可行性。

1 “风-光”协调规划的上层优化模型

分布式风机(wind turbine，WT)和分布式光伏(photovoltaic，PV)出力具有波动性和不确定性，但是在时序特性上具有一定的互补性。一方面，利用分布式电源出力在时间维度上的互补特性，通过合理配置WT和PV容量，可以降低PV和WT的波动性，使其出力在每个时刻能够稳定地满足部分负荷功率。另一方面，在配置过程中，考虑分布式电源出力与负荷需求的协调互动特性，优化分布式电源容量，在满足负荷需求的同时，可以在负荷低谷期间减少“弃风”和“弃光”现象，提高能源利用率。

1.1 目标函数

上层优化模型在考虑分布式电源投资和运维费用的同时，加入了负荷侧从电网购电费用的目标因素。负荷购电费用的多少与WT-PV互补能力的强弱存在较强的耦合关系，如果WT-PV配置方案的互补特性好，与负荷的协调能力强，则WT-PV能较好地满足负荷需求及“风光”资源被尽可能地消纳，避免出现大规模的“弃风弃光”现象，负荷侧的购电费用相应会降低。目标函数可以表示为

minF=F1+F2

(1)

式中：F1表示分布式电源的投资、运维费用；F2表示规划区域配电网负荷从电网的购电费用和配电网线路的有功网损费用。F1与F2的单调特性后续会进行分析。

1.1.1分布式电源的投资、运维费用

根据市场上现有的分布式电源参数，PV的最小安装容量由光伏板的面积决定，容量可以连续变化，最小可至几十W，最大可至MW级；而WT的安装容量则是由装机台数和最小单机容量决定，安装容量与装机台数存在阶跃变化的特点。因此，在目标函数中，对PV容量和WT台数分别定义为连续变量EPV和离散变量NWT，F1表示为

(2)

(3)

(4)

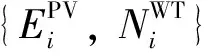
1.1.2规划区域负荷从电网的购电费用、配电网线路的有功网损费用

F2=O3+O4

(5)

(6)

(7)

(8)

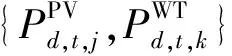
(9)

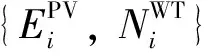
1.2 约束条件

PV和WT的接入应满足系统的潮流平衡以及网络安全约束。为满足规划区域对分布式电源渗透率的要求，本文模型设置了考虑渗透率大小的PV和WT容量约束。

(1)潮流平衡约束：

(10)

(2)节点电压约束：

Vmin,i≤Vi,t≤Vmax,i

(11)

式中：Vi,t为节点i在t时刻的电压；Vmin,i和Vmax,i为节点i电压下限和上限。

(3)线路容量约束：

0≤Iij,t≤Imax,ij

(12)

其中

Iij,t=|Yij|×[(Vi,t)2+(Vj,t)2-
2Vi,tVj,tcosθij,t]1/2

(13)

式中：Imax,ij为线路ij的热稳定极限；Vi,t、Vj,t分别为节点i、j在t时刻的电压；θij,t为t时刻节点i、j的功角差；Yij为系统的节点导纳矩阵元素。

(4)PV和WT容量约束。在实际装机过程中，为了保证配电网系统供电的可靠性，对接入的间歇性能源发电容量进行限制，描述如下：

(14)

(15)

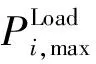
1.3 PV和WT的出力模型

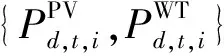
(1)PV出力模型。在上层优化模型中，光伏各个时刻出力的大小可由对应时刻的工作温度、光照条件以及厂家标定参数计算得出：

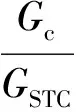
(16)

式中：EPV为厂家标定的地面光伏组件标准测试条件(STC)下的额定容量；GSTC=1 000 W/m2；TSTC=25 ℃；Gc为太阳能电池板实际工作时的太阳辐照度；Tc为太阳能电池板的实际工作温度；功率温度系数k=0.004 5[18]。

(2)WT出力模型。在上层优化模型中，风机各个时刻的出力大小可由以下分段函数进行计算：

(17)

式中：vc为切入风速；vr为额定风速；vco为切出风速；vt为WT实际工作时的风速；EWT为风机的额定功率。

2 基于储能削峰填谷运行策略的下层规划模型

接入风机和光伏的配电网，由于分布式电源出力的间歇性会加剧系统的功率波动。储能系统由于其充放一体，响应迅速的特点，具备很强的削峰填谷能力。在进行储能系统的选址定容之前，本文提出了一种满足储能系统削峰填谷能力的运行策略，基于该运行策略完成后续的选址定容工作。

2.1 考虑削峰填谷能力的储能系统运行策略

储能系统削峰填谷的能力体现在对负荷波动的补偿能力，目标函数中考虑使用储能系统所接入节点负荷大小的二阶中心距表示，目标函数如式(18)所示：

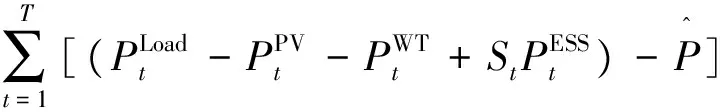
(18)

(19)

考虑储能系统自身的物理特性，约束条件应包括储能系统的充放电功率、容量和状态约束。

(1)储能系统的充放电功率约束：

(20)

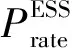
(2)储能系统的充放电容量约束：

(21)

式中：SOCmin和SOCmax分别为储能系统的最小荷电状态和最大荷电状态；EESS为储能系统的规划容量。

(3)储能系统的充放电状态约束：

∀St∈{-1,0,1}

(22)

该约束使用整数集表示储能系统放电、浮充、充电的3种状态。

图1 变量和EESS变化时可行域与最优解位置的变化情况Fig.1 Location of feasible region and optimal solution when

(23)

2.2 储能系统的定容

而对于不等式约束(21)的处理，无法采用以上方法寻找变量EESS的代替值。确定变量EESS的过程即储能的定容过程。基于以上储能系统削峰填谷运行策略，本文提出了一种储能容量的估算方法。如图2所示，储能系统的运行策略目的在于补偿功率波动，以24 h为储能系统的1个运行周期，储能系统的补偿目标是负荷功率尽可能小，接近于负荷平均功率。因此，按照此原则在图中划分了充电时段和放电时段，阴影包含的范围即需要储能系统补偿的容量。

图2 储能系统充放电时段划分Fig.2 Charging and discharging time division of ESS

该过程的数学表达式如下：

(24)

(25)

(26)

2.3 储能系统的选址

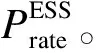
该模型的数学描述如下所示：

(27)

(28)

(1)储能系统的容量约束：

(29)

在节点k处安装储能系统的容量应满足等式(24)—(26)。

(2)储能系统的充放电功率约束：

(30)

储能的充放电功率应满足2.1节的运行策略，且储能的额定充放电功率应等于运行策略中产生的最大功率。

(3)储能系统的安装位置约束：

∀k∈{1,2,3,…N}

(31)

式中N为储能系统的备选安装节点号。

3 模型的求解策略

3.1 上层模型的求解

潮流平衡约束的引入使上层模型成为混合整数非凸优化问题，基于常规数值解析的数学规划方法难以实现模型约束的松弛或者线性变化，进而实现模型非凸到凸的变换。因此，凸优化方法难以在该问题上进行应用。而随机智能算法在求解优化问题上不存在对模型凸性的要求，对模型具有一定的泛性。本文采用遗传算法作为求解策略的外部框架，在计算种群的适应度中嵌套入牛顿-拉夫逊法完成潮流等式方程的计算，这样就避免了采用数值计算法非凸部分的求解，能够在有限时间内得到一个较好的解。值得注意的是，上层模型中同时存在连续和离散变量，而遗传算法对于离散和连续变量的操作算子不同，因此在应用遗传算法进行求解时，选择、重组、变异操作应按2个种群进行操作。算法求解的框架如图3所示。

图3 多种群进化的遗传算法计算流程图Fig.3 Flow chat of multi-population genetic algorithm

3.2 下层模型的求解

在第2节模型的描述部分已经介绍，对于区间约束左右端点存在变量的情况下难以确定问题的最优解。因此，下层模型的求解关键在于储能系统的容量估算和最大充放电功率的确定。基于本文的估算方法，利用YALMIP工具箱可以完成储能系统运行策略的求解，进一步确定储能系统的充放电功率配置。最后计算各个备选节点储能系统的配置成本和维护成本，以成本最优的节点作为储能系统的安装节点，从而完成选址工作。

本文整体的求解思路如图4所示。

4 算例仿真

4.1 算例介绍

本文算例采用IEEE-33节点标准配电系统[20]，系统的基准电压为12.66 kV，配电网区域的拓扑图如图5所示。区域的主变压器位于节点0处。该配电网区域内的历史负荷水平、辐照度、风速、温度等参数作为系统的输入数据，如图6所示。分布式风机电源采用Bergey Power的Excel-6型风机，单台风机的额定功率为5.5 kW，风机的切入风速、额定风速和切出风速分别为2.5、11和60 m/s。分布式光伏电源采用Solar Tech公司的SPM065P-F型，相关投资和运维费用如表1所示，各个节点接入风机和光伏电源的容量不超过节点年最大负荷功率值的30%。在等年值计算中，设备的投资年限为15年，贴现率为6%。储能系统采用钠硫电池，相关的计算参数如表2所示。储能系统安装的备选节点为1，5，17，21，24和32。

图4 双层规划模型的求解流程图Fig.4 Flow chat of bi-level planning model

图5 IEEE-33标准配电系统Fig.5 IEEE-33 standard distribution system

图6 功率、温度、风速、光照数据及春夏秋冬聚类曲线Fig.6 Power, temperature, wind speed, illuminationdata and clustering curves in spring, summer, autumn and winter

表1风机和光伏电源成本
Table1WTandPVcost

表2 钠硫电池储能系统参数Table 2 Parameters of sodium sulfur batteryenergy storage system

4.2 仿真结果

4.2.1上层模型的优化结果

在使用遗传算法计算时，每个个体都需要进行潮流计算以适应模型中潮流约束的要求，随着输入计算数据时间序列的延长，算法在迭代中计算潮流的次数也越来越多，大大降低了求解速度。但是，如果输入的计算数据序列过短，虽然求解速度快，但是输出的配置方案对规划年限内运行状况的适应性则较差，甚至在部分极端情况下，比如负荷的峰值产生电压偏移、线路容量越限或者在负荷低谷期间产生反送功率等。考虑到以上问题，在仿真计算时本文设置了2种仿真策略：场景一是基于仿真算例中全序列数据的遍历计算；场景二是采用K均值聚类方法，将算例中全序列数据按照春夏秋冬进行聚类，得到96点的数据序列，如图6浅色线所示。仿真计算的收敛特性如图7和图8所示。综合对比2种策略的计算结果和计算时长如表3所示，各个节点风机和光伏电源的容量配置结果如图9所示。

图7 基于全序列数据计算的遗传算法性能跟踪Fig.7 Performance tracking of genetic algorithmsbased on full sequence data

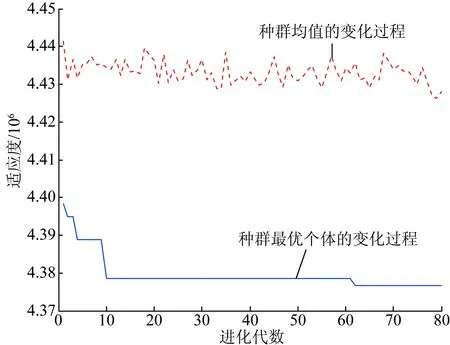
图8 基于K-means聚类的96点数据计算的遗传算法性能跟踪Fig.8 Genetic algorithm performance tracking of 96 pointdata calculation based on K-means clustering

图7和图8遗传算法的性能跟踪显示算法收敛特性良好，不同数据长度下均能完成最优解的搜索。如表3所示，全序列数据的计算时长远高于96点数据的计算时长，这是由于数据序列计算长度不同，数据序列越长，个体在遗传算法适应度计算中需要的潮流计算次数就越多，种群中寻优耗费的时间也就越长。

表3不同策略下配置费用优化结果对比
Table3Comparisonofoptimalresultsunderdifferentcomputingstrategies

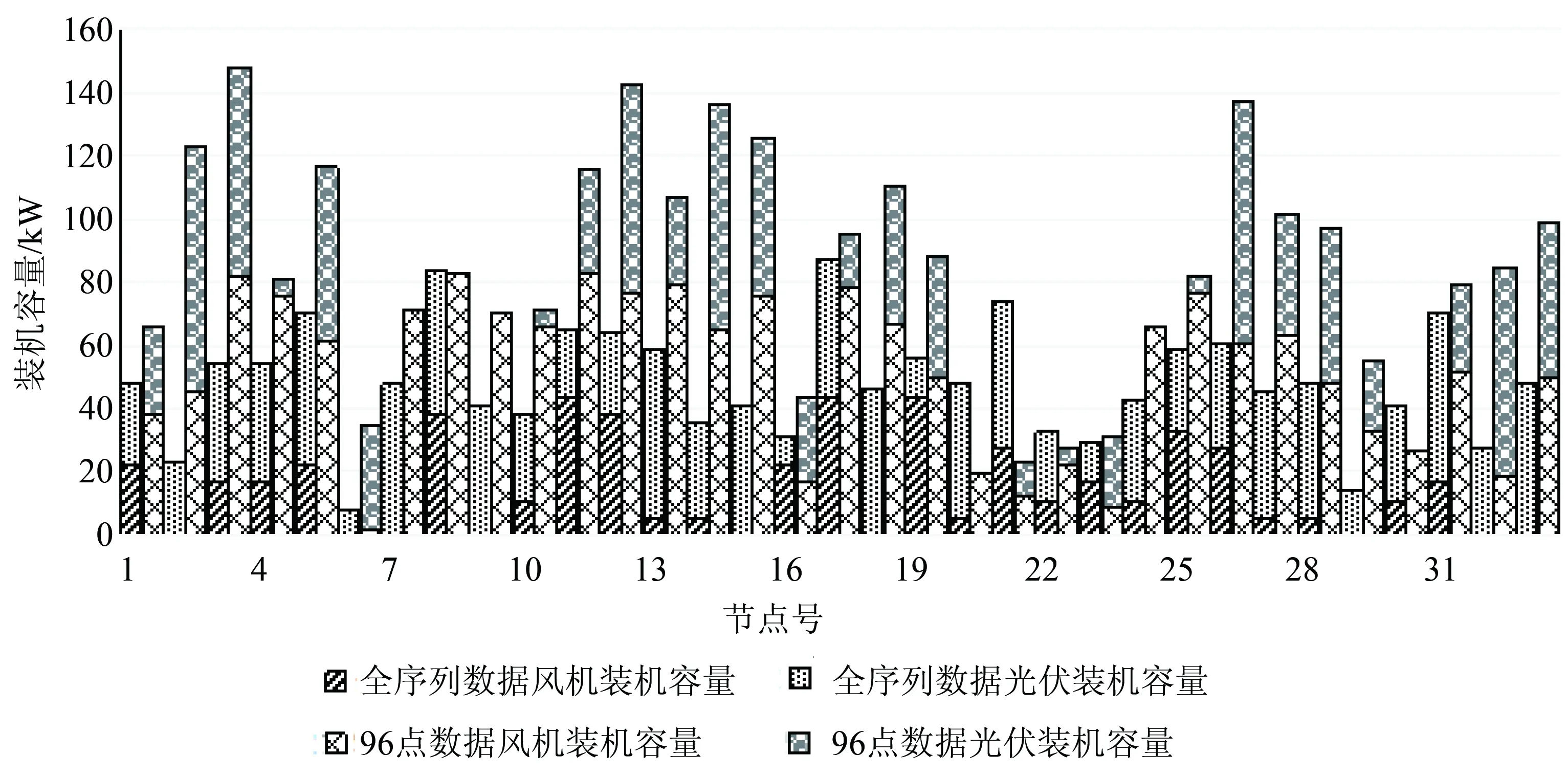
图9 不同计算策略下各个节点风机、光伏的配置容量对比Fig.9 Allocation capacity comparison of WT and PV ineach node under different computing strategies

观察表3中各项费用的计算结果，96点的配置结果均低于全年序列数据计算的配置结果，这是由聚类算法导致的。聚类后的数据相比于聚类前数据体量小，原始数据值要高于按春夏秋冬聚类后得到的数据值。因此，按照96点数据模拟原有全序列数据长度得到的结果要小，无法考虑系统运行的极端情况，但求解时间却得到了缩减。全序列数据的计算虽然耗时较长，但随着数据序列在时间维度的延长，所产生的优化方案适应性更好，尤其是区域购电费用及网损费用更接近于未来运行的实际情况。

上层优化模型帕累托解的分布特点如图10所示，纵坐标F1表示分布式电源的投资和运维费用，横坐标F2表示规划区域从电网的购电费用和配电网线路的有功网损费用。利用聚类后的96点数据进行模型的帕累托分析，令权重系数在0到1之间均匀变化，变化的步长为0.01。权重系数为1时，表示仅优化分布式电源的投资和运维费用，反之，权重系数为0表示仅优化配电网区域从电网的购电费用和线路的有功网损费用。观察上层模型帕累托解的分布特点，在权重系数发生变化时，解的位置逐渐向两坐标轴靠近。虽然投资费用与区域购电费用及网损费用具有统一量纲，可以进行线性加权。但是，在进行优化时如果仅进行简单的线性加权，则无法获得满足投资人员规划需求的折中解。投资及运维费用在数值上远高于区域购电及网损费用，数值大的目标函数在优化中会影响其他目标函数最优解的搜索。因此，在进行规划方案制定时，应注意不同目标函数之间的数量级关系，根据规划人员对优化目标的决策意向，选取合理的权重系数。

图10 上层优化模型帕累托解的分布特点Fig.10 Distribution characteristics of Pareto solution atupper level model

4.2.2下层模型的优化结果

对接入风机和光伏电源的配电网区域负荷再次进行聚类，获得基于全年数据的负荷典型特性曲线，如图11所示。基于该数据对每个节点储能容量和充放电功率进行配置。储能系统的容量裕度系数取1.5，根据等式(24)—(26)得到容量及充放电功率配置结果如表4所示。根据表2给出的钠硫电池参数，计算备选节点的储能系统配置成本，计算结果如表5所示。通过表5中数据可以观察到，容量配置成本在综合成本中所占比重较大。又由于下层模型中负荷特性对储能优化配置结果影响较大，算例区域较小，图11所示聚类后区域内各个节点的负荷特性变化趋势相近，因此储能系统在各个节点配置的综合成本相差较小。

图11 K-means聚类后节点1—33的全年典型负荷特性曲线Fig.11 Annual typical load characteristic curve ofnode 1—33 after K-means clustering

表5 储能系统综合配置成本Table 5 Comprehensive cost of ESS 美元/a

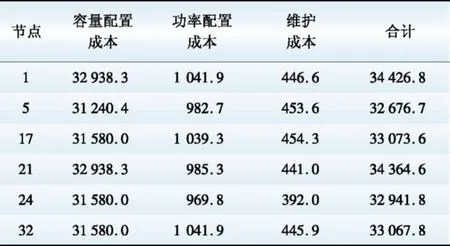
根据计算结果，各个备选节点储能系统配置成本的优选次序为5、24、32、17、21、1。以系统的末端节点17为例绘制配置储能系统前后，负荷功率的变化情况如图12所示。观察到在配置储能系统后负荷功率的波动性得到明显降低，基于削峰填谷的储能系统运行策略效果良好。

5 结 论

(1)所构建模型能完成配电网区域内风机、光伏电源和储能系统的配置工作，求解算法可输出收敛的规划方案，并通过帕累托分析调整目标函数的权重系数可取得满足不同规划人员需求的规划方案。

图12 接入储能系统前后节点17功率变化情况Fig.12 Power change of node 17 before andafter ESS connection

(2)研究了不同序列长度数据对模型规划结果的影响，数据序列越长，成本计算值则越接近实际运行情况，但相应规划方案的求解时间越长。

(3)研究了储能系统满足削峰填谷需求的运行策略，基于该策略提出了储能系统容量、充放电功率的配置方案，完成储能系统选址工作并以节点数据为例仿真验证了配置方案平抑波动的效果。

[1] ISLE D, VAZIRI M, ZARGHAMI M，et al. Review of concepts to increase distributed generation into the distribution network[C]//2014 Sixth Annual IEEE Green Technologies Conference.Corpus Christi, TX, USA:IEEE, 2014: 118-125.

[2] 邢海军,程浩忠,张沈习,等, 主动配电网规划研究综述[J]. 电网技术, 2015, 39(10): 2705-2711.

XING Haijun, CHENG Haozhong, ZHANG Shenxi, et al. Review of active distribution network planning[J]. Power System Technology, 2015, 39(10): 2705-2711.

[3] 王成山,王守相. 分布式发电供能系统若干问题研究[J]. 电力系统自动化, 2008, 32(20): 1-8.

WANG Chengshan, WANG Shouxiang. Study on some key problems related to distributedgeneration systems [J].Automation of Electric Power Systems, 2008, 32(20): 1-8.

[4] 马钊, 梁惠施, 苏剑. 主动配电系统规划和运行中的重要问题[J]. 电网技术, 2015, 39(6):1499-1503.

MA Zhao, LIANG Huishi, SU Jian, et al. Important issues in planning and operation of active distribution system[J]. Power System Technology, 2015, 39(6): 1499-1503.

[5] 宋艺航, 谭忠富, 李欢欢, 等. 促进风电消纳的发电侧、储能及需求侧联合优化模型[J]. 电网技术, 2014, 38(3): 610-615.

SONG Yihang, TAN Zhongfu, LI Huanhuan, et al. An optimization model combining generation side and energy storage system with demand side to promote accommodation of wind power[J]. Power System Technology, 2014, 38(3): 610-615.

[6] 修晓青,李建林,惠东. 用于电网削峰填谷的储能系统容量配置及经济性评估[J]. 电力建设, 2013, 34(2): 1-5.

XIU Xiaoqing, LI Jianlin, HUI Dong. Capacity configuration and econemic of energy storage system for grid peak load shifting[J]. Electric Power Construction, 2013, 34(2): 1-5.

[7] 曾鸣,杨雍琦,刘敦楠,等. 能源互联网“源-网-荷-储”协调优化运营模式及关键技术[J]. 电网技术, 2016, 40(1): 114-124.

ZENG Ming, YANG Yongqi, LIU Dunnan, et al. “Generation-grid-load-storage” coordinative optimal operation mode of energy internet and key technologies [J]. Power System Technology, 2016, 40(1): 114-124.

[8] 张涛,张福兴,张彦. 面向能源互联网的能量管理系统研究[J]. 电网技术, 2016, 40(1): 146-155.

ZHANG Tao, ZHANG Fuxing, ZHANG Yan. Study on energy management system of energy Internet [J]. Power System Technology, 2016, 40(1): 146-155.

[9] 杨敏霞,刘高维,房新雨,等. 计及电网状态的充放储一体化站运行模式探讨[J]. 电网技术, 2013, 37(5): 1202-1208.

YANG Minxia, LIU Gaowei, FANG Xinyu, et al. Discussion on operation mode of charging-discharging-storage integrated station considering power network statuses [J]. Power System Technology, 2013, 37(5): 1202-1208.

[10] MONTOYAO D, GRAJALES A, GARCES A, et al.Distribution systems operation considering energy storage devices and distributed generation [J]. IEEE Latin America Transactions, 2017, 15(3): 890-900.

[11] ING K G, JAMIANJ J, MOKHLIS H A, et al. Optimum distribution network operation considering distributed generation mode of operations and safety margin [J]. IET Renewable Power Generation, 2016, 10(8): 1049-1058

[12] 李逐云,雷霞,邱少引,等. 考虑“源-网-荷”三方利益的主动配电网协调规划[J]. 电网技术, 2017, 41(2): 378-387.

LI Zhuyun, LEI Xia, QIU Shaoyin, et al. Coordinated planning of active distribution network considering “source-grid-load” benefit[J]. Power System Technology, 2017, 41(2): 378-387.

[13] 欧阳邵杰,曾博,邱泽晶,等. 面向用户差异化需求的智能配电网综合资源优化规划和配置方法[J]. 电力建设, 2017, 38(2): 38-44.

OUYANG Shaojie, ZENG Bo, QIU Zejing, et al. Integrated resource optimizing planning and allocation method of intelligent distribution network for differentiated demands of users [J]. Electric Power Construction, 2017, 38(2):38-44.

[14] 高红均,刘俊勇,魏震波,等. 主动配电网分层鲁棒规划模型及其求解方法[J]. 中国电机工程学报, 2017, 37(5): 1389-1401.

GAO Hongjun, LIU Junyong, WEI Zhenbo, et al. A bi-level robust planning model of active distribution network and its solution method [J]. Proceedings of the CSEE, 2017, 37(5): 1389-1401.

[15] 李秀磊,耿光飞,季玉琦,等. 考虑实际运行的配电网电池储能系统的优化配置研究[J]. 电力系统保护与控制,2017,45(9):88-94.

LI Xiulei, GENG Guangfei, JI Yuqi, et al. Study on optimal allocation of battery energy storage in distribution network considering the actual operation [J]. Power System Protection and Control,2017,45(9):88-94.

[16] 王彦虹,邰能灵,嵇康. 含大规模风光电源的配电网储能电池选址定容优化方案[J]. 电力科学与技术学报,2017,32(2):23-30.

WANG Yanhong, TAI Nengling, JI Kang. Optimal battery storage allocation in distributed network with large-scale of wind and photovoltaic generation [J]. Journal of Electric Power Science and Technology,2017,32(2):23-30.

[17] 郭金明,李欣然,邓威,等. 基于2层规划的间歇性分布式电源及无功补偿综合优化配置[J]. 中国电机工程学报, 2013, 33(28): 25-33.

GUO Jinming, LI Xinran, DENG Wei, et al. Comprehensive optimal allocation of intermittent distributed generation and reactive power compensation based on bilevel planning[J].Proceedings of the CSEE, 2013, 33(28): 25-33.

[18] GAVANIDOUSE S, BAKIRTZISA G. Design of a stand alone system with renewable energy sources using trade off methods [J]. IEEE Transactions on Energy Conversion, 1992, 7(1): 42-48.

[19] 张节潭,程浩忠,胡泽春,等. 含风电场的电力系统随机生产模拟[J]. 中国电机工程学报,2009,10(28):34-39.

ZHANG Jietan, CHENG Haozhong, HU Zechun, et al. Power system probabilistic production simulation including wind farms [J]. Proceedings of the CSEE, 2009, 10(28): 34-39.

[20] BARANM E，WU F F. Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Transactions on Power Delivery, 1989, 4(2): 1401-1407.

2017-06-15

刘源(1993)，男，硕士研究生，主要研究方向为配电网规划技术、新能源接入；

杨军(1977)，男，教授，博士生导师，主要研究方向为电力系统运行与控制、电动汽车、新能源接入技术；

杨丙权(1965)，男，高级工程师，主要从事电力系统调度与运行方面的工作;

朱旭(1994)，男，硕士研究生，主要从事多能流系统规划方面的工作;

陈艳(1974)，女，高级工程师，主要从事电力系统规划评审方面的工作;

王宣(1988)，女，工程师，主要从事电力系统规划评审方面的工作。

(编辑 张小飞)

Bi-LevelPlanningMethodforDistributionNetworkwith‘WT-PV-Load-ESS’

LIU Yuan1, YANG Jun1, YANG Bingquan2, ZHU Xu1, CHEN Yan2, WANG Xuan2

(1. School of Electrical Engineering, Wuhan University, Wuhan 430072, China; 2. Wuhan Power Supply Company, State Grid Hubei Electric Power Company, Wuhan 430013, China)

The research on distribution generation and energy storage system in distribution network is a hot topic of current research. This paper proposes a bi-level planning model of ‘WT-PV-Load-ESS’ in distribution network. The upper model is optimized for the investment amp; maintenance cost, and the power purchase and power losses cost are also taken into account in the allocation of PV and WT. The lower model proposes a operation strategy of ESS for peak shaving, based on which the sizing amp; sitting work of ESS are completed. Aiming at the above model, the following solutions are proposed in this paper: the upper model is solved based on genetic algorithm; the influence of the length of the input data on the planning results is compared byK-means clustering method; Pareto analysis is used to study the relationship between the investment amp; maintenance cost and the power purchase amp; power loss cost; at last, based on the estimation of ESS’s capacity, the strategy of ESS is solved with YALMIP toolbox, then the sizing amp; sitting work of ESS are completed. Finally, the effectiveness of the proposed model in the planning of ‘WT-PV-Load-ESS’ system are verified through the simulation of IEEE-33 node standard distribution system. The results show that the proposed ESS operation strategy has good effect in peak shaving.

wind turbine (WT); photovoltaic (PV);energy storage system (ESS); bi-level optimization; genetic algorithm (GA);K-means clustering

国家自然科学基金项目(5127713); 国网湖北省电力公司科技项目(增量配电模式下城市电网规划技术研究)

Project supported by National Natural Science Foundation of China(5127713)

TM714

A

1000-7229(2017)11-0087-10

10.3969/j.issn.1000-7229.2017.11.012