考虑异质性的定频空调负荷聚合建模及功率跟踪策略

楼家辉，杨欢，王京，汤胜清，赵荣祥，郑太英

(浙江大学电气工程学院，杭州市 310027)

考虑异质性的定频空调负荷聚合建模及功率跟踪策略

楼家辉，杨欢，王京，汤胜清，赵荣祥，郑太英

(浙江大学电气工程学院，杭州市 310027)

为便于建立空调负荷聚合模型，目前研究往往假设空调个体参数一致，忽略了空调受控群内部参数差异较大的实际情况，亦未计及空调最小停运时间与整数设定温度的影响，因此该文考虑空调负荷的异质性，提出一种改进型聚合建模方法。该方法根据空调额定制冷量分组，并通过模糊C-均值聚类算法提高受控群电功率的模拟精度。引入最小停运时间以及设定温度的整数约束，使仿真结果更接近实际定频空调运行工况。同时，在实际运算中采用坐标格式存储稀疏矩阵，提高运算速度和模型的实用性。基于该改进型聚合模型，进一步提出一种功率跟踪策略，该策略计算各聚类群每一时刻的需求响应能力，通过求解0—1整数规划问题实现调控对象最优组合。仿真算例验证所提策略对目标功率跟踪的良好效果。

需求响应；定频空调；聚合模型；聚类；功率跟踪

0 引 言

近年来，我国坚持低碳发展理念，重视可再生能源的开发利用。以风电为例，截至2015年底，全国风电装机总量已达到128.3 GW，居世界首位[1]。由于风电、太阳能发电等可再生能源普遍具有间歇性、波动性的特点，引起电力潮流的不确定性，而增加备用容量、新建调峰机组等常规手段难以兼顾经济性要求，需要通过源-网-荷的有效互动，特别是负荷柔性调控来满足可再生能源的消纳要求[2-4]。

空调负荷占我国城市夏季用电峰荷的比重接近一半，且呈现出不断上升的趋势，所形成的短时负荷尖峰引起极大的电力供需矛盾，给电网的安全稳定运行带来隐患[4-5]。单纯采取增加电源投资应对电力尖峰的方法会造成资源配置效率的低下，不能满足经济性要求，近些年来通过基于激励的需求响应和基于电价的需求响应来缓解供需矛盾得到工业界和学术界越来越多的重视[6]。考虑到空调负荷及所在建筑物具有良好的储能储热特性，在满足人体舒适度要求下，可以通过优化启停设置，实现调控时间内空调所属建筑物环境中热能和电能的相互转换，不仅消除其自身对电网带来的短时负荷冲击，而且具备消纳可再生能源的潜力[4-6]。

城市环境中，无论是家庭用户还是工商业用户，其所拥有的空调数量都是庞大的，需要通过负荷聚合商对这类中小型负荷进行资源整合、统一调度与控制[6]。聚合商若以空调单体为控制对象，通过单体模型得到一段时间内空调群的总体特性，一方面会消耗较长的数值计算时间，另一方面控制逻辑过于复杂难以实现。因此，有必要对空调群建立聚合模型，以聚合体为调度控制对象参与系统运行[6-7]。关于定频空调聚合建模的方法包括经聚类的等效热力学参数模型[7]、蒙特卡洛模拟[8]、状态队列[9]和状态空间[10-12]等方法。文献[10]基于一阶空调单体模型，推导各状态单元的负荷密度流量，计算每一时刻的负荷密度分布，得到有限维的状态空间模型。文献[11]在文献[10]的基础之上，通过将单输入单输出模型扩展为三输入单输出模型，解决了模型中状态转移矩阵时变的问题。文献[12]考虑各空调所处环境等效比热容的差异，计算不同状态单元之间的转移概率。然而，上述基于状态空间的聚合建模方法适用于空调及其所处环境参数相同，或仅考虑单一参数存在差异的情形，无法准确反映实际空调群的多种参数差异性。

在面向需求响应应用的空调群温度设定点控制方法的研究中，文献[10-11]通过调节温度设定值变化速率使空调群电功率跟随参考功率曲线，满足可再生能源消纳要求，但在建模和控制过程中没有考虑最小停运时间的因素。当室内温度下降到临界温度，空调会短时停运，此时制冷系统高低压管冷媒压力未平衡，压缩机无法响应设定温度控制信号并正常启动[13]。在平衡高低压管压力差的最小停运时间内，空调压缩机始终处于关停状态，模型中并未反映这一情形，造成电功率模拟出现偏差。文献[14]改进了对空调群温度设定值整体调节的方法，提出了一种基于局部终端温度调节的控制策略，使用户的舒适度要求得到了满足。文献[15]基于状态队列模型，通过设定温度上下限的分离控制，克服了传统温度设定值改变后负荷短时间内剧烈变化的现象。但以上控制策略所依赖的精确、非离散值调节设定温度在目前的空调终端暂时难以实现。

针对目前研究中存在的上述问题，本文以定频空调群为研究对象，从以下几方面开展具体研究工作：

(1)考虑空调群的异质性，通过额定制冷量分组以及模糊C-均值聚类预处理，提高聚合模型对内部参数差异较大的空调群电功率的模拟精度。

(2)在基于状态空间的空调聚合模型中计及最小停运时间和设定温度整数调节的约束，使后续控制策略设计过程更加符合实际。同时考虑到状态转移矩阵呈现出的高度稀疏性，通过坐标格式(coordinate format，COO)存储，提高动态过程模拟的计算效率。

(3)基于改进的聚合模型，提出功率跟踪策略。通过计算各聚类群每一时刻的需求响应能力，求解0—1整数规划问题，进行调控对象最优组合，实现精确的功率跟踪。

1 定频空调单体模型

定频空调系统单体建模是空调群聚合建模的基础，涉及2方面的研究内容：空调所属建筑物环境的热力学建模和空调机组的运行状态建模。前者在于构建空调制冷量与室内温度之间的函数关系，后者是为了描述对应一定的室内温度，空调的电功率与制冷量情况。

1.1 热力学建模

对于空调所属建筑物环境的热力学建模，国内外文献常采用一阶等效热参数模型[6]：

(1)

式中：Ti为空调所处建筑物环境的室内温度；To为室外温度；R为房间等效热阻；C为房间等效热容；Q为空调制冷量。

1.2 运行状态建模

空调的运行状态模型由式(2)—(4)给出：

(2)

式中：s(t)为t时刻空调启停状态；Tset为空调的设定温度；δ表示空调状态切换临界温度与设定温度的差值。

(3)

式中Qr表示空调的额定制冷量。

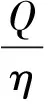
(4)

式中：P表示空调的电功率；η为能效比。

式(1)—(4)以设定温度为输入变量，电功率为输出变量，建立了定频空调的热电耦合模型，通过数值计算可以得到单个空调的动态响应情况。

2 空调群分组及聚类预处理

本文将考虑空调额定制冷量Qr、房间等效热阻R和房间等效热容C差异形成的异质性，以内部参数差异较大的受控群为研究对象，提出分组及聚类预处理的方法，使得同一聚类群中受控端的参数尽可能相似。

无论是家用还是工商业用定频空调，其额定制冷量遵循一定的规格，呈现出数值离散化特征。这使得根据额定制冷量大小将空调群分成有限组，组内空调额定制冷量相同成为了可能。在预处理阶段，先将具有相同额定制冷量的空调分为一组，共m组。

分组后，对于第p个(1≤p≤m)空调组，通过聚类降低组内个体响应速度(温升/温降速率)之间的差异。由式(1)可得，当空调所处区域室外温度相同时，位于同一状态单元(室内温度相近、启停状态一致)的空调其温升/温降速率与2项指标RC和Q/C有关。在实际应用中，负荷聚合商可通过参数辨识得到这2项特征指标[6]。

本文采用模糊C-均值聚类算法[16]，基于这2项指标对m个空调组分别进行聚类，每组形成q个聚类群，用各聚类中心分别代表m×q个聚类群群内个体的特征指标，具体步骤如下：

(5)

(2)设定每组聚类数q以及迭代停止阈值ε，在矩阵X′中随机抽取q个样本，将q个样本的值赋给初始聚类中心zl(l=1,2,…,q)，zl= [zl1,zl2]。

(6)

(7)

(5)更新各聚类中心zl。

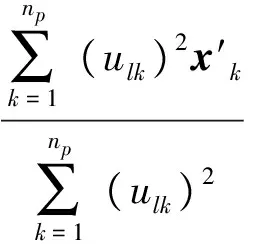
(8)

(6)计算此次迭代的目标函数F(t)。

(9)

图1为对负荷群进行分组聚类预处理的流程示意图。

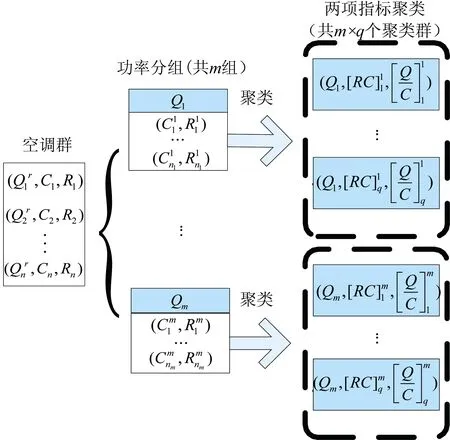
图1 空调群分组聚类示意图Fig.1 Grouping and clustering process of airconditioning group

3 聚合建模

3.1 改进聚合模型整体框架

文献[11]提出了三输入单输出的状态空间聚合模型，3种输入量包括设定温度变化率、设定温度较初始值改变量以及室外温度较初始值改变量，输出量为空调群总电功率。它将整个空间划分为若干个单元，根据各受控端初始启停状态及室内温度将其纳入相应的单元内，计算每一单元中空调总量与单元间距之比，定义为负荷密度，量纲为“个/℃”。建立状态转移矩阵用于反映各状态单元之间负荷密度流向关系，通过数值计算，模拟各单元内负荷密度的动态变化过程。功率-密度向量用于表示各单元内单位负荷密度所对应的电功率，从而间接得到总电功率随时间的变化过程。

上述模型包含设定温度变化率这一控制变量，仅适用于温度设定点变化缓慢的控制过程，需要施加于能接受精确、非离散温度设定值的空调设备，一般的家用、工商业空调难以达到。当温度设定值整数变化时，设定温度变化率近似无穷大，故原有数学模型无法适用。此外，原有模型中没有考虑空调压缩机最小停运时间，高估了能响应控制指令的受控群体数量。基于以上认识本文对模型进行改进，改进后聚合模型反映的空调负荷密度流如图2所示(密度流即各状态单元间空调负荷密度的转移关系)。

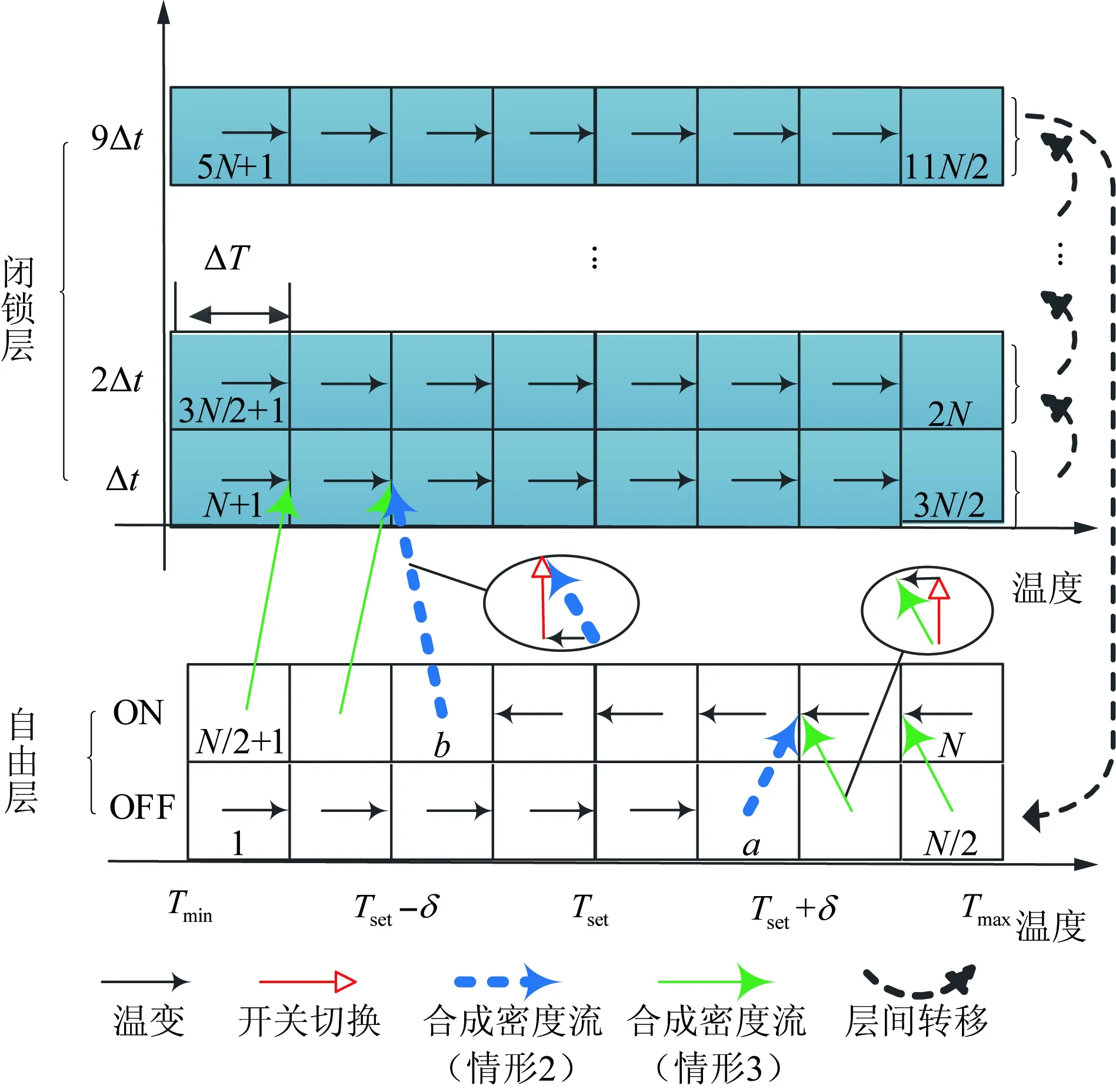
图2 单步长内空调负荷密度流(仿真步长Δt=20 s)Fig.2 Air conditioning load density current at eachtime step (simulation step is 20 s)

自由层包括ON/OFF 2种运行状态，以ΔT为温度间隔，划分成N个可响应控制指令的状态单元。根据各受控端初始时刻的启停状态及室内温度将其纳入相应的单元内，计算各单元负荷密度。自由层状态单元间负荷密度流存在3种情形：

(1)只存在温变引起的密度流，如图2中序号为1—a-1和b1—N的单元格。

(2)先发生温变，然后温度达到临界温度引起开关切换，在这2部分共同作用下构成合成密度流，如图2中序号为a和b的单元格。

(3)温度已超过临界温度，需先经过开关切换，然后在新的状态单元内发生温变，如图2中序号为a1—N/2和N/21—b-1的单元格。

闭锁层计及了空调最小停运时间的影响。当空调处于制冷工作状态，室内温度下降到临界温度Tset-δ时，压缩机会短时停止运行。此时高低压管压力差较大，需要经过至少3 min的停机时间来平衡压力差，使机组正常启动[17]。模型中仿真步长与后续负荷聚合商下发控制指令的时间间隔一致，为降低控制过程中的通信要求，参考文献[11]的设置，将仿真步长h取为20 s。对应3 min的最小停运时间，闭锁层应包含9层，各状态单元序号为N1—11N/2。对于这些闭锁层状态单元，每隔1个仿真步长负荷密度向上转移1层。在闭锁层期间受控端无法响应设定温度控制来切换开关状态，压缩机始终关停，但存在温变引起的密度流。

基于第2节分组聚类预处理结果，可对各聚类群分别建立聚合模型，相应的状态空间方程如式(10)所示。其中前一式计算各状态单元内负荷密度(单元内空调总量与单元间距之比)的变化率，因单元内空调总量的变化率可以表示为所有与之关联单元(存在密度流向关系)的温升/降速率与负荷密度乘积之和[10]，故写成此等形式。后一式基于各状态单元负荷密度与电功率的对应关系，求出总电功率。

(10)

式中：x=[x1,...,x5.5N]T是状态向量，表示每一状态单元内的负荷密度；y是输出变量，表示聚类群的总电功率；D和F是不随时间变化的状态转移矩阵，℃/h，无量纲；G是时变的状态转移修正矩阵，3个矩阵共同作用，用于反映不同情形下关联单元的温升/降速率；v表示t时刻设定温度Tset与初始设定温度Tset_base之差；w表示t时刻室外温度To与初始室外温度To_base之差；ΔT为各状态单元的温度间隔。

下文对自由层和闭锁层中负荷密度流如何在状态空间方程中体现，以及各矩阵中元素取值和结构进行说明。

3.2 自由层状态单元间负荷密度流

对于情形1中温变引起的负荷密度流，用αon和αoff分别表示温降和温升速率，结合式(1)可得

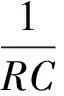
(11)

将To=To_base+w,Tset=Tset_base+v代入上式有

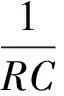
(12)

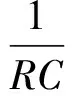
同理可得：

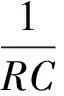
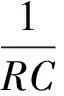
(13)

式中：αon_base表示初始温降速率；αoff_base表示初始温升速率；To_base表示初始室外温度；Tset_base表示初始设定温度。

式(10)中D=diag[D1,D2,...,D11]为一个5.5N× 5.5N阶矩阵，呈现出高度稀疏性。其中D1和D2均为0.5N× 0.5N阶矩阵。

(14)

(15)

式(10)中矩阵F=diag[F1,F2,...,F11]，同样为5.5N× 5.5N阶矩阵。矩阵F1和F2结构分别与矩阵D1和D2一致，内部元素取值上将αoff_base和αon_base用-1替代。

对于情形2中的合成密度流，在D、F矩阵基础上，通过与设定温度取值相关的矩阵G(Tset)来修正。对应图2，此时有4个状态单元的密度流向关系发生变化。

Ga+1,a=-αoff,Gb-1,b=αon,

Ga+N/2,a=αoff,Gb+N/2,b=-αon

(16)

其中前2式用于取消单元格a和a1，b和b-1之间的关联，避免单元格a、b中负荷密度分别流向单元格a1和b-1中。后2项建立新的关联，因开关切换使单元格a、b内负荷密度流向与其运行状态相异，温度区间相同的单元，即单元格aN/2、bN/2。

对于情形3中合成密度流的开关切换部分，在每一个仿真步长的开端，瞬时转移相应状态单元的负荷密度。其表达式为(例如对t-1时刻到t时刻进行动态模拟)：

(17)

式中i=a1,...,0.5N；j=0.5N1,...,b-1。

之后温变部分的处理同样基于矩阵D和F。

3.3 闭锁层状态单元间负荷密度流

考虑最小停运时间之后，增加了若干闭锁层，对于这些闭锁层状态单元，其温变规律与状态单元1～N/2相同，故状态转移矩阵D和F中相应元素设置为

Di=D1,Fi=F1

(18)

式中i= 3,…,11。

此外，在每个仿真步长的开端，对闭锁层和自由层中处于停机状态的状态单元进行层间负荷密度转移：

(19)

3.4 稀疏矩阵COO格式存储

通过聚合模型的改进，后续控制策略设计更加符合实际，但算法的复杂度也相应增加。预处理中的分组聚类基于设备和所处建筑物环境参数，可以离线完成，但对受控群的动态过程在线模拟需要借助各聚类群的聚合模型分别计算加总。同时，由于考虑了空调最小停运时间，增加了闭锁层，使得D、F等矩阵的维数增加，这些都会增加对空调群动态过程模拟的时长。

结合D、F矩阵的结构特点，采用存储稀疏矩阵常用的COO格式(如图3所示)，提高全过程模拟的计算效率。

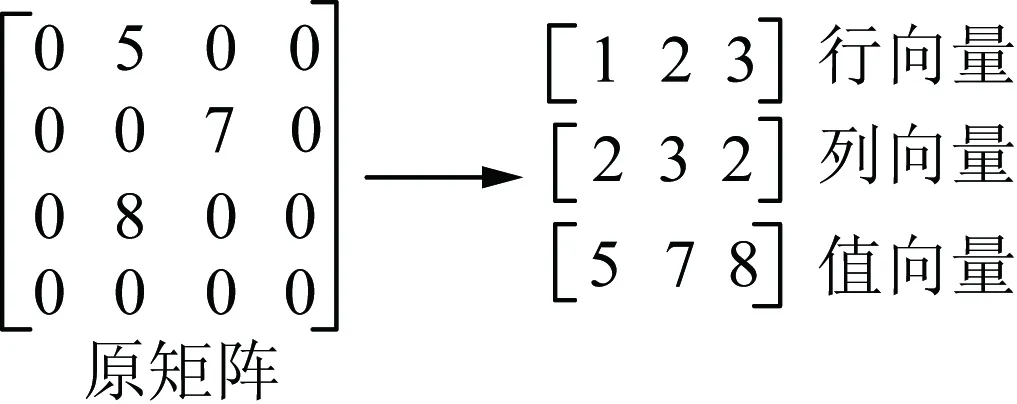
图3 COO存储格式Fig.3 COO storage format

3.5 基于改进聚合模型的负荷群动态过程仿真

将本文提出的经预处理的改进聚合模型与单体模型[6]和传统聚合模型[11]进行对比，检验其对负荷群动态特性模拟的精度。本文为了分析负荷异质性的情况，在参考文献[11]给出的受控端参数的基础上，对其中R、C的取值在原值(R=2 ℃/kW,C= 10 (kW·h)/℃)基础上给予50%的偏差，在取值范围内呈均匀分布。同时，各空调额定制冷量取13～18 kW之间的整数值，即13、14、15、16、17、18 kW，各类台数之比为1∶2∶2∶3∶1∶1。鉴于模型推导建立在单步长内密度流发生在相邻2个状态单元之间的基础之上[10]，为满足这一前提条件，对ΔT提出要求，需保证

αonh≤ΔT,αoffh≤ΔT

(20)

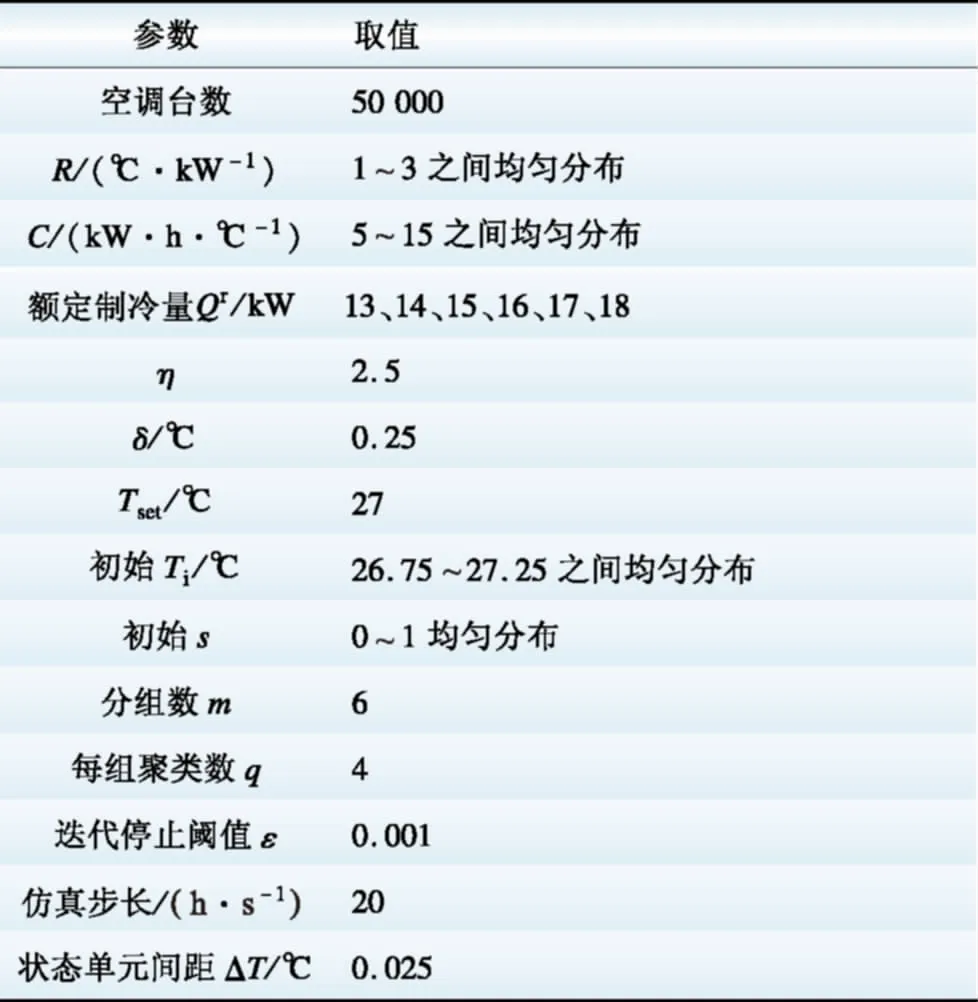
仿真所用参数如表1所示。

表1仿真所用参数值
Table1Simulationparameters

室外温度变化情况如图4所示[11]。

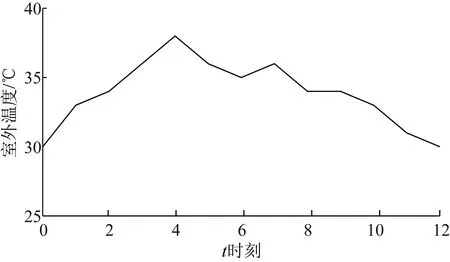
图4 室外温度变化Fig.4 Variation of outdoor temperature

采用配备3.60 GHz CPU、8 GB内存的计算机，在Matlab 2016a环境下模拟受控群电功率动态过程。其中单体模型仿真采用式(1)—(4)联立构成的方程组对各台空调分别计算，再加总得到空调群总体的电功率变化曲线。鉴于单体模型已较为成熟，对于描述家庭用户和小型工商业用户空调制冷环境具有较高的精度[6,15]，图5以单体模型模拟结果作为比较基准。为了验证改进聚合模型能计及最小停运时间的影响，在式(2)中加上对已关停时间的判断语句，在单体模型仿真过程中体现，将其作为图6的比较基准。采用不同模型时的模拟效果如图5、图6所示。

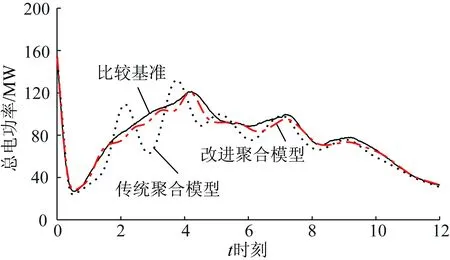
图5 不同方法模拟动态响应对比(设定温度不变) Fig.5 Comparison of dynamic responses amongdifferent methods (fixed setting temperature)

图6 不同方法模拟动态响应对比(设定温度整数调节) Fig.6 Comparison of dynamic responses amongdifferent methods (setting temperature adjustmentwith integer constraints)

图5给出了设定温度不变情况下空调群的动态响应。可以看到，传统聚合模型由于用受控群平均R、C、Qr作为模型参数，当内部参数差异较大时，对动态响应过程的模拟会有较大误差。改进聚合模型通过设置m×q个聚类群，聚类群内部设备参数与各聚类中心较为相近，提高了模拟精度。同时采用了COO格式存储后，全过程仿真时间从553 s降至36 s，提高了在线应用的时效性。

图6反映了本文提出的改进聚合模型在考虑设定温度整数调节，并计及最小停运时间之后，对空调群动态响应模拟的良好效果。设定温度初始值仍然设置为27 ℃，在第30 min调整为28 ℃，在第31 min调整为26 ℃，此后不发生变化。与传统聚合模型无法应用于此场景仿真相比(原因在3.1节中简述)，改进聚合模型在设定温度整数调节情况下仍能保证较高的模拟精度。同时，在第31 min设定温度下降后，在第30 min关停的一部分空调由于受最小停运时间限制并不会迅速开启，在第33 min之后才会陆续开启，基于改进聚合模型的仿真结果能表现出计及最小停运时间约束对功率变化过程的影响。

4 控制策略

考虑到可再生能源出力具有间歇性、波动性的特点，会给系统平衡带来较大挑战。单纯调度常规机组，容易受其爬坡速率约束，无法足额消纳可再生能源。能量管理中心可以根据当地刚性负荷电功率预测以及新能源超短期出力预测，以常规机组和负荷聚合商的总调度成本最小化为目标，进行日内不平衡功率最优分配，将负荷聚合商的参考功率曲线下发。负荷聚合商以此为跟踪目标，调度负荷侧资源，改变空调群设定温度进行响应，达到跟踪消纳可再生能源的目的[11,18]。

定义负荷压缩/提升能力为聚类群设定温度提升/降低1 ℃引起的负荷密度转移，所间接改变的电功率(已达到设定温度上下限则响应能力记为0)。

(21)

其中，c,d,e,f由式(22)给出。

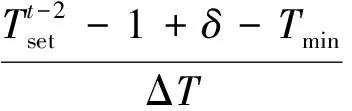
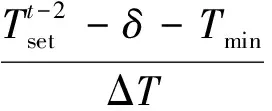
(22)

本文主要探讨负荷聚合商如何对给定跟踪目标进行跟踪，相应的控制策略如图7所示。

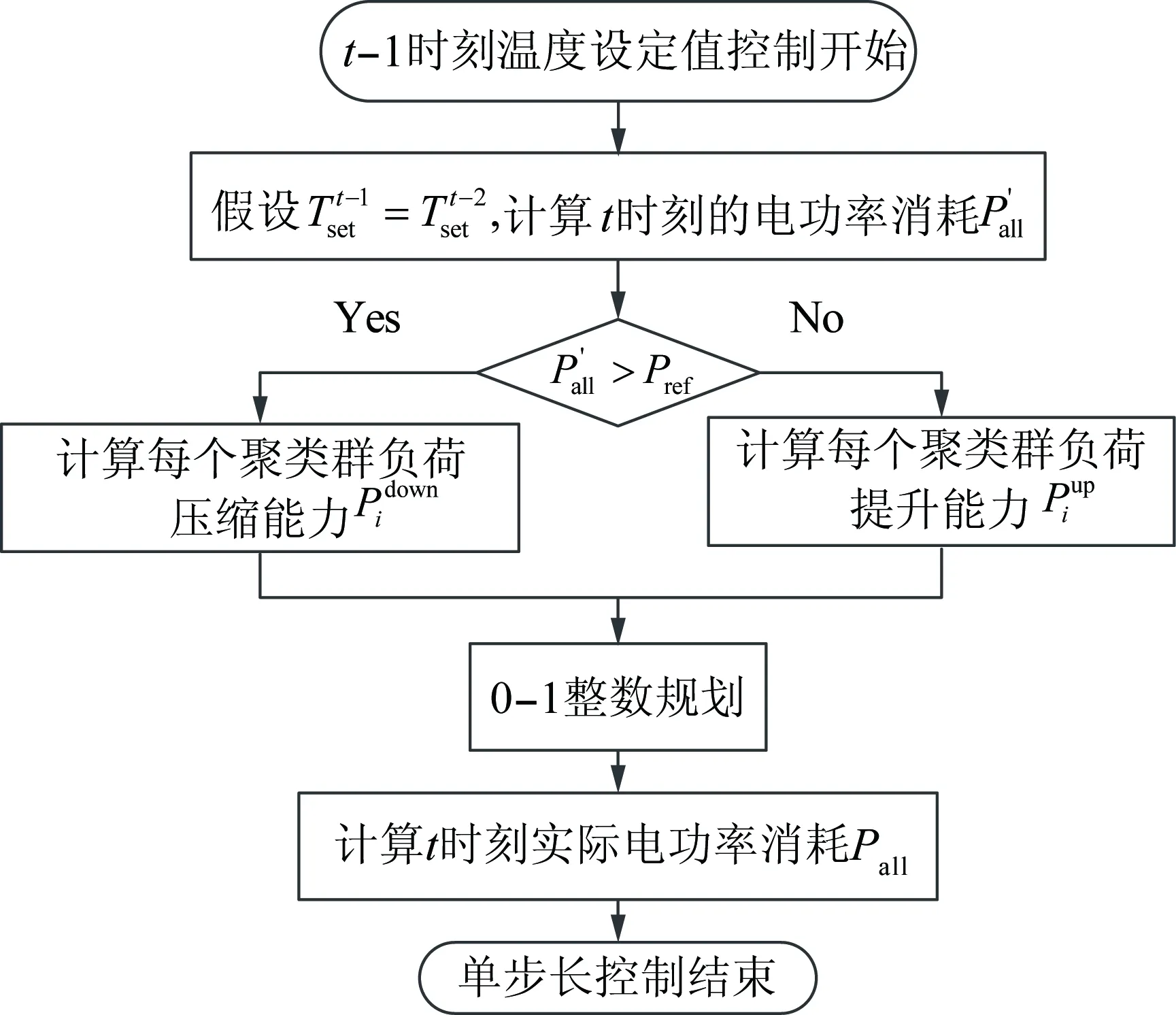
图7 功率跟踪控制策略流程图Fig.7 Flow chart of power tracking control strategy

基于式(10)求得温度设定值不调整条件下的总功率消耗，对跟踪误差进行预估。

(23)

通过求解0—1整数规划问题得到t-1时刻各聚类群温度设定值的最优组合。当预估功率消耗不足时有

(24)

若解得ri=1，则将t-1时刻第i个聚类群的设定温度调低1 ℃，再通过数值计算求解t时刻受控群实际电功率。预估功率过大时控制策略类似。

5 功率跟踪仿真算例

选取文献[18]算例中能量管理中心基于经济调度，下发给负荷聚合商的参考功率曲线作为跟踪目标。场景定位为多个智能社区集聚形成的小型电力系统，共20 000台空调参与，其他参数同表1。社区家庭或商铺的空调用户均签订了激励响应合同，由负荷聚合商对参与需求响应的用户给予经济补偿(本文暂不讨论用户补偿方案的制定)，所有终端能够接收负荷聚合商的控制信号并调节自身设定温度。考虑人体温度舒适度要求，令温度设定值调节范围为26，27，28 ℃共3档。在功率跟踪过程中，负荷聚合商基于控制策略，以20 s为周期，向各聚类群下发温度设定值。从图5和图6可以看到，在短时间内，改进聚合模型对各聚类群的动态响应模拟具有较高的精度，负荷聚合商基于初始值的模拟，能够较好掌握各集群的状态信息，降低了各空调终端运行状态信息的上传频率要求。综上，由于空调负荷地域分布范围较小，且并不依赖于频繁的双向通信，故仿真中通信延迟的影响可以忽略不计。

将本文所提控制策略与文献[18]的PI调节方法进行对比，功率跟踪结果如图8所示。可以看到，本文方法与PI调节对参考功率曲线的跟踪效果相当，全过程跟踪相对误差不超过2.5%，如图9所示。但从图10可以看到，PI调节是以设定温度变化率为控制量，通过对空调设定温度进行微小调整来改变功率输出，这在目前普通空调终端难以实现。本文所提跟踪策略对温度设定点进行整数调节，能在满足跟踪精度的同时，降低对受控群设定温度调节精度的要求，具有一定应用价值。

6 结 论

针对现有基于状态空间方程的聚合模型的不足，以及定频空调的实际工况，本研究提出了一种计及空调负荷异质性的聚合建模方法。该方法依据空调额定制冷量分组，以等效热阻和等效热容为特征指标，采用模糊C-均值聚类算法对负荷群进行预处理。同时，考虑空调最小停运时间及设定温度整数调节的要求，对整个状态单元架构和密度流进行调整，并采用COO格式存储稀疏矩阵，降低矩阵维数增加后对仿真时间的不利影响。经与传统方法对比，改进后的聚合建模方法具有较高的模拟精度和计算效率。进一步设计了功率跟踪策略，基于对各聚类群需求响应能力的计算，通过求解0—1整数规划问题实现了任一仿真步长内温度设定值组合最优。仿真算例验证了该策略能较好地跟踪目标功率。整个调控过程中设定温度满足用户舒适度要求，不增加电源侧调度负担，为消纳可再生能源提供了可能。

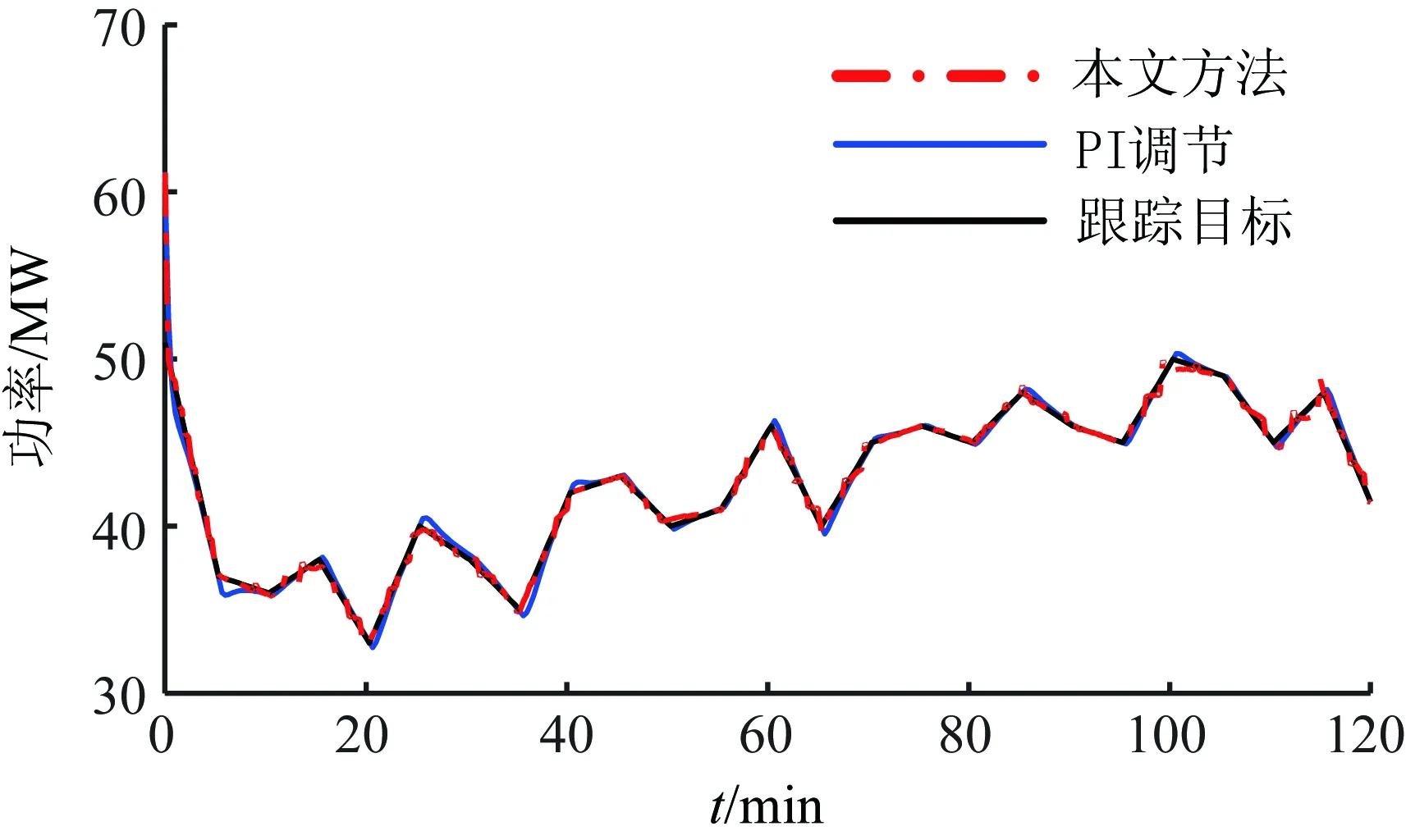
图8 功率跟踪结果Fig.8 Results of power tracking

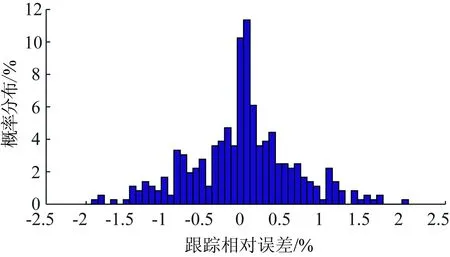
图9 跟踪相对误差概率分布Fig.9 Probability distribution of relative tracking errors

图10 PI调节的控制量Fig.10 Control quantity of PI regulation

[1] 彭小圣，熊磊，文劲宇，等．风电集群短期及超短期功率预测精度改进方法综述[J].中国电机工程学报，2016，36(23)：6315-6326, 6596．

PENG Xiaosheng，XIONG Lei，WEN Jingyu，et al．A summary of the state of the art for short-term and ultra-short-term wind power prediction of regions[J]．Proceedings of the CSEE，2016，36(23)：6315-6326, 6596．

[2] 李禹鹏，冯楠，崔勇，等．考虑风电不确定性及柔性负荷的安全约束机组组合问题研究[J]． 电力建设，2017，38(2)：129-137．

LI Yupeng，FENG Nan，CUI Yong，et al．Security constrained unit commitment problem considering wind power uncertainty and flexible load[J]．Electric Power Construction，2017，38(2)：129-137．

[3] 曾鸣，杨雍琦，刘敦楠，等．能源互联网“源-网-荷-储”协调优化运营模式及关键技术[J]． 电网技术，2016，40(1)：114-124．

ZENG Ming，YANG Yongqi，LIU Dunnan，et al．“Generation-grid-load-storage” coordinative optimal operation mode of energy internet and key technologies[J]．Power System Technology，2016，40(1)：114-124．

[4] 徐青山，杨辰星，颜庆国．计及规模化空调热平衡惯性的电力负荷日前削峰策略[J]．电网技术，2016，40(1)：156-163．

XU Qingshan，YANG Chenxing，YAN Qingguo．Strategy of day-ahead power peak load shedding considering thermal equilibrium inertia of large-scale air conditioning loads[J]．Power System Technology，2016，40(1)：156-163．

[5] 徐青山，吴枭，杨斌．考虑状态差异性聚类的空调负荷直接负荷控制动态优化方法[J] ．电力系统自动化，2016，40(14)：33-42．

XU Qingshan，WU Xiao，YANG Bin．Dynamic optimization method of direct load control for air-conditioning load considering status diversity clustering[J]．Automation of Electric Power Systems，2016，40(14)：33-42．

[6] 宋梦，高赐威，苏卫华．面向需求响应应用的空调负荷建模及控制[J]．电力系统自动化，2016，40(14)：158-167．

SONG Meng，GAO Ciwei，SU Weihua．Modeling and controlling of air-conditioning load for demand response applications [J]．Automation of Electric Power Systems，2016，40(14)：158-167．

[7] 管国兵，辛洁晴．空调负荷群分组控制方法[J]．电力系统自动化，2016，40(20)：40-46．

GUAN Guobing，XIN Jieqing．Grouping control method for air conditioning load[J]．Automation of Electric Power Systems，2016，40(20)：40-46．

[8] 李娜，褚晓东，张文，等．考虑参数空间差异的多区域空调负荷聚合模型[J]．电力系统及其自动化学报，2012，24(5)：19-24．

LI Na，CHU Xiaodong，ZHANG Wen，et al．Aggregation model of multi-zone air conditioning load considering spatial differences of parameters[J]．Proceedings of the CSU-EPSA，2012，24(5)：19-24．

[9] LU N，CHASSIN D P．A state-queueing model of thermostatically controlled appliances[J]．IEEE Transactions on Power Systems，2004, 19(3)：1666-1673．

[10] BASHASH S，FATHY H K．Modeling and control of aggregate air conditioning loads for robust renewable power management[J].IEEE Transactions on Control System Technology，2013，21(4)：1318-1327．

[11] HU J Q，CAO J D，CHEN M Z，et al．Load following of multiple heterogeneous TCL aggregators by centralized control[J]．IEEE Transactions on Power Systems，2017，32(4):3157-3167．

[12] LIU M X，SHI Y，LIU X T．Distributed MPC of aggregated heterogeneous thermostatically controlled loads in smart grid[J]．IEEE Transactions on Industrial Electronics，2016，63(2)：1120-1129．

[13] 郭永吉．中央空调温度控制系统研究[D]．兰州：兰州理工大学，2008．

GUO Yongji．The control system research on temperature of central air-conditioning[D]. Lanzhou: Lanzhou University of Technology, 2008.

[14] 戚野白，王丹，贾宏杰，等．基于局部终端温度调节的中央空调需求响应控制策略[J]．电力系统自动化，2015，39(17)：82-88．

QI Yebai，WANG Dan，JIA Hongjie，et al．Demand response control strategy for central air-conditioner based on temperature adjustment of partial terminal devices[J]．Automation of Electric Power System，2015，39(17)：82-88．

[15] 周磊，李扬，高赐威．聚合空调负荷的温度调节方法改进及控制策略[J]．中国电机工程学报，2014，34(31)：5579-5589．

ZHOU Lei，LI Yang，GAO Ciwei．Improvement of temperature adjusting method for aggregated air-conditioning loads and its control strategy[J]．Proceedings of the CSEE，2014，34(31)：5579-5589．

[16] LYER N S，KANDEL A，SCHNEIDER M．Feature-based fuzzy classification for interpretation of mammograms[J]．Fuzzy Sets System，2000，114(2)： 271-280．

[17] 蒋爱国．户用多功能太阳能热泵系统的实验研究[D]．合肥：中国科学技术大学，2008．

JIANG Aiguo．Experimental study on a domestic multifunctional solar assisted heat pump system[D]. Hefei: University of Science and Technology of China, 2008.

[18] HU J Q，CAO J D，YONG T Y，et al．Demand response load following of source and load systems[J]．IEEE Transactions on Control Systems Technology，2017，25(5)：1586-1598．

2017-06-19

楼家辉(1992)，男，硕士研究生，主要研究方向为电力需求侧管理；

杨欢(1981)，男，通信作者，副教授，博士生导师，主要研究方向为微电网与并网变换器控制、主动负荷与智能配用电；

王京(1994)，男，硕士研究生，主要研究方向为永磁同步电机系统建模与仿真；

汤胜清(1977)，男，博士研究生，主要研究方向为微电网在电力系统中的应用；

赵荣祥(1962)，男，教授，博士生导师，主要研究方向为交流调速系统、并网变换器容错运行、分布式发电与微电网、储能及其应用等；

郑太英(1982)，男，讲师，主要研究方向为电力系统保护、新能源等。

(编辑 刘文莹)

ConstantFrequencyAirConditioningLoadAggregatedModelingandItsPowerTrackingStrategyConsideringHeterogeneity

LOU Jiahui, YANG Huan, WANG Jing, TANG Shengqing, ZHAO Rongxiang, ZHENG Taiying

(College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China)

To simplify the aggregated model for air conditioning loads, uniform parameters are usually assumed in recent research. However, the actual situation that the parameters of controlled air-conditioning group are significantly various, and the influence of the minimum outage time and integer setting temperature are neglected. This paper proposes an improved aggregated modeling method considering the heterogeneity of air conditioning loads, which improves the power simulation precision of the controlled group through grouping air conditioners by rated refrigeration capacity and using fuzzy C-means clustering algorithm. By introducing the minimum outage time and setting temperature adjustment with integer constraints, the simulation scenarios became closer to the actual operation condition of constant frequency air conditioning. Besides, in the actual calculation, the sparse matrix was stored in the coordinate format to improve the calculation speed and practicability of the model. Based on the improved aggregated model, a power tracking strategy is proposed consequently, which calculates the demand response capacity of each cluster at each time step, and optimizes the regulating objects by solving the 0-1 integer programming problem. The simulation results verify the effectiveness of the proposed strategy in power tracking.

demand response; constant frequency air conditioning; aggregated model; clustering; power tracking

浙江省自然科学基金资助项目(LY15E070003)

TM73

A

1000-7229(2017)11-0055-09

10.3969/j.issn.1000-7229.2017.11.008