数列综合检测(A卷)答案与提示
2017-11-27
数列综合检测(A卷)答案与提示
一、选择题
1.A

5.B 提示:因为第一天派出64人,第二天开始每天派出的人数比前一天多7人,所以第5天派出64+4×7=92(人),前5天共派出因此,前5天应发大米:390×3=1170(斤)。
6.C 提示:数列 {l g an} 的前8项和S8=lga1+lga2+…+lga8=lg(a1·a2·…·a8)=lg(a1·a8)4=lg(a4·a5)4=4。

8.B 提示:设等差数列an{}的公差为d,已知a1=2,a5=3a3,故2+4d=3(2+2d),解得d=-2。
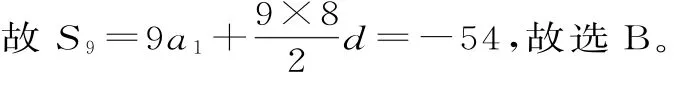
9.A 提示:由题意知,a3a4a7q=a3a7(a4q)=a3a7a5=a35=8,∏9=a1a2a3…a9=a95,所以∏9=83=512,故选A。
10.A提示:因为a1=S1=a+b,a2=S2-S1=2a,a3=S3-S2=6a,所以q=3,
11.A 提示:设三个正数分别为:2-d,2,2+d,由题意得:b3=2-d+3=5-d,b4=2+6=8,b5=2+d+13=15+d,所以82=(5-d)(15+d),解得d=1。b3=4,b4=8,b5=16,q=2,b1=1,故bn=2n-1,选A。
12.A 提示:A选项中当等比数列{an}和{bn}的项数不同时,{anbn} 不是等比数列,故选A。
13.C 提示:因为a1>0,a6a7<0,所以a6>0,a7<0,等差数列的公差小于零。a3+a10=a1+a12>0,a1+a13=2a7<0。又因为Sn>0的最大自然数n的值为12,故选C。

15.A 提示:符合条件的n位数可分为2类:(1)当首位是2时,则余下n-1位数符合条件的个数为f(n-1);(2)当首位是1时,则第2位是2,余下n-2位数符合条件的个数为f(n-2)。于是f(n)=f(n-1)+f(n-2),f(n)为斐波那契数列。因为f(1)=2,f(2)=3,所以计算可得f(10)=144。

17.D 提示:①当k=0时,则数列成了常数列,则分母也为0,进而推断出k不可能为0,①正确。
②当等差数列为常数列时不满足题设的条件,故②不正确。
③当等比数列为常数列时不满足题设的条件,故③不正确。


二、填空题
21.4 n+2 提示:设第n个图案中白色地砖有an块,则a1=6,a2=10,a13=14。易知an-an-1=4(n≥2),故an{}是以6为首项,4为公差的等差数列,an=4n+2。

23.60 提示:因为S10,S20-S10,S30-S20成等差数列,且S10=10,S20=30,S20-S10=20,所以S30-30=30,S30=60。
24.n2+n 提示:依题意知a22=a1a4,(a1+d)2=a1·(a1+3d),将d=2代入上式求得
25.2 提示:由已知得a3a5=a24=64,且an>0,所以a4=8,a6=32。因此,q24,q=2,q=-2(舍去)。。又当n=1时,a=1,也适合上式,故该1数列的通项公式是

30.1375 提示:由题意知an=4(-1)nn+(-1)nn2,令S1=(-1)1·12+(-1)2-22+(-1)3·32+…+(-1)10502,S2=4×(-1)1×1+4×(-1)2×2+…+4(-1)50×50,所以S50=S1+S2。则S1=(-1)1×12+(-1)2×22+…+(-1)50×502,即S1=-1+22-32+…-492+502=1+2+3+…+50=1275。又S2=4[2-1+4-3+…+50-49]=100,S50=S1+S2=1275+100=1375。

35.3 n-1 提示:题中条件可表示为f(1,1)=2,f(m,n)=k,则f(m,n+1)=k+3,于是有f(m,n+1)-f(m,n)=3,即输入的两个数据中第一个数据不变,第二个数据增加1时,输出的结果增加3,亦即f(m,1),f(m,2),f(m,3),…,f(m,n),…,成等差数列,公差为3,故f(1,n)=2+(n-1)×3=3n-1。
36.72 提示:已知a1=2,且对任意正整数k,l,都有ak+l=ak+al,可令k=n,l=1,得an+1=an+a1,即an+1=an+2,所以{an}是首项为2,公差为2的等差数列,从而有an=2n,故Sn=n(n+1),S8=72。
37.9 提示:由题意知2Sn=a2n+an,①2Sn+1=a2n+1+an+1。②
②-①,得2an+1=a2n+1+an+1-a2n-an。

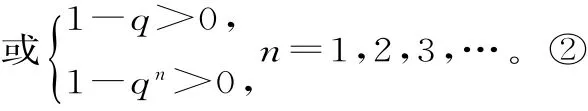
解①式得q>1。解②式,由于n可为奇数,可为偶数,得-1<q<1。q的取值范围是(-1,0)∪(0,+∞)。

三、解答题
41.设t1,t2,…,tn+2构成等比数列,其中t1=1,tn+2=100,则:
Tn=t1·t2…tn+1·tn+2,①
Tn=tn+2·tn+1…t2·t1。②
①×②得:
T2n=(t1tn+2)·(t2tn+1)…(tn+1t2)·(tn+2t1)=102(n+2)。
故an=lgTn=n+2(n≥1)。
42.设数列cn{}的公比为q,由题意可知c1+c2=10,c2+c3=40,解得c1=2,q=4。{故cn=2·4n-1=22n-1。
an=log222n-1=2n-1。

43.设an为(2013+n)年年底分红后的资金,其中n∈N*,则a1=2×1000-500=1500,a2=2×1500-500=2500,…,an=2an-1-500(n≥2)。
由题意知an-500=2(an-1-500)(n≥2),故数列{an-500}是以1000为首项,2为公比的等比数列,则an-500=1000×2n-1。
故an=1000×2n-1+500。
(1)a4=1000×24-1+500=8500,该企业2017年年底分红后的资金为8500万元。
(2)由an>32500,即2n-1>32,得n>6,该企业从2020年开始年底分红后的资金超过32500万元。


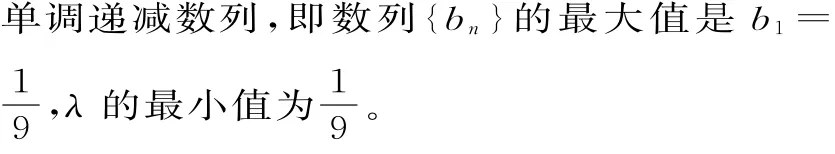
48.(1)设数列{an}的公差为d,依题意,2,2+d,2+4d成等比数列,故有(2+d)2=2(2+4d),解得d=0或d=4。
当d=0时,an=2,a2,a5的值均为2;
当d=4时,an=4n-2,则a2=6,a5=18。
(2)当an=2时,Sn=2n。显然2n<60n+800,此时不存在正整数n,使得Sn>60n+800。


