数列综合测试题（B卷）答案与提示

数列综合测试题（B卷）答案与提示

一、填空题

1.B 提示:数列的通项公式不唯一,有的数列没有通项公式,所以①④不正确。

2.C

3.B

4.B 提示:由题意知:a3=a2-a1=3,a4=-3,a5=-6,a6=-3,a7=3,a8=6,

a9=3,a10=-3,…,故{an}是周期为6的数列,a2016=a6=-3。

6.C对任意的n∈N*恒成立,因此,logq2＜nmin,logq2＜1,即0＜q＜2。又0＜q＜1,则0＜q＜1。当q=1时,对任意的n∈N*,有S2n＜3Sn成立。综上可得,0＜q≤1。

18.B 提示:由题意,a1+a2+a3+…+a100=12-22-22+32+32-42-42+52+…+992-1002-1002+1012=-(1+2)+(3+2)-…-(99+100)+(101+100)=-(1+2+…+99+100)+(2+3+…+100+101)=100。

19.C

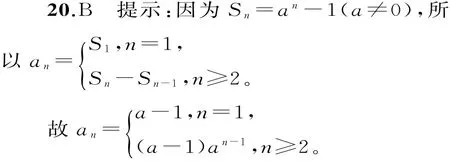
当a=1时,an=0,数列{an}是一个常数列,也是等差数列;当a≠1时,数列{an}是一个等比数列。

21.D 提示:等比数列{an}的通项公式为an=2n-1,数列{bn}通项公式为bn=2n,所以Sn=n2+n。

当n≤3时,cn+1＞cn,当n=4时,cn+1=cn,当n≥5时,cn+1＜cn,故cn取最大值时,n的值是4或5。

22.C

24.C 25.D 26.C 27.C 28.D 29.C 30.D 31.B 32.A 33.C 34.C 35.A

二、填空题

36.n

37.50 提示:因为{an}为等比数列,所以由已知可得a10a11=a9a12=a1a20=e5,则lna1+lna2+…+lna20=ln(a1a2a3…a20)。

而a1a2a3·…·a20=(a1a20)10=(e5)10=e50,因此lna1+lna2+…+lna20=50。

39.211 提示:当n＞1时,Sn+1+Sn-1=2(Sn+S1),可以化为(Sn+1-Sn)-(Sn-Sn-1)=2S1=2,即n＞1时,an+1-an=2,即数列{an}从第二项开始组成公差为2的等差数列,所以S15=a1+(a2+…+a15)=211。

当n=1时,a1=S1=26;

当n≥2时,an=Sn-Sn-1=2×3n+1。

46.1306 提示:由题设可得a2n+a2n+1=n+1。

取n=1,2,3,…,49可得a2+a3=2,a4+a5=3,a6+a7=4,…,a98+a99=50,将以上49个等式两边分别相加可得a2+a3+49=1274。又a3=a1+1=2,a6=3-a3=1,a12=6-a6=5,a25=a12+1=6,a50=25-a25=19,a100=50-a50=31,所以S100=1+1 274+31=1306。

47.p=2或3 提示:因为数列{cn+1-pcn}为等比数列,所以(cn+1-pcn)2=(cnpcn-1)(cn+2-pcn+1)。

将cn=2n+3n代入上式得:

[2n+1+3n+1-p(2n+3n)]2=[2n+2+3n+2-p(2n+1+3n+1)]·[2n+3n-p(2n-1+3n-1)]。

三、解答题

48.(1)由于an+1=(n2+n-λ)an,n=1,2,…,且a1=1,把a2=-1代入上式得-1=2-λ,故λ=3。

从而a3=(22+2-3)×(-1)=-3。

(2)数列 {an}不可能为等差数列,证明过程如下:

由a1=1,an+1=(n2+n-λ)an,得:

a2=2-λ,a3=(6-λ)(2-λ),a4=(12-λ)(6-λ)(2-λ)。

若存在λ,使{an}为等差数列,则a3-a2=a2-a1,即(5-λ)(2-λ)=1-λ,解得λ=3。于是a2-a1=1-λ=-2,a4-a3=(11-λ)(6-λ)(2-λ)=-24。这与{an}为等差数列矛盾。所以,不存在λ使{an}是等差数列。

49.(1)由Sn=2an-a1得Sn-1=2an-1-a1(n≥2),所以an=2an-1(n≥2)。

因为a1,a2+1,a3成等差数列,所以a1+a3=2(a2+1),即a1+4a1=2(2a1+1),解得a1=2。

从而an≠0,于是得到

数列{an}是以2为公比的等比数列,所以求数列{an}的通项公式an=2n。

=-(n-5)2+25,当n=5时,Sn取得最大值。

52.(1)设数列{an}的公差为d,数列{bn}的公比为q。

因为m,t为正整数,所以t只能取2,3,5。

当t=2时,m=7;当t=3时,m=5;

当t=5时,m=4。

所以存在正整数t,使得b1,b2,bm成等差数列。

55.(1)设等比数列的公比为q,因为a1,a4,a13分别是等比数列{bn}的b2,b3,b4项,所以(a1+3d)2=a1(a1+12d)。

又a1=3,所以d2-2d=0,解得d=2或d=0(舍去)。

所以an=3+2(n-1)=2n+1。

整理得Tn=(n-1)2n+1+2(n∈N*)。

59.(1)当n=1时,S1=2a1-22,得a1=4。

Sn=2an-2n+1。

当n≥2时,Sn-1=2an-1-2n,两式相减得an=2an-2an-1-2n,即an=2an-1+2n。

编者的话:同学们在演练的过程中,如果需要更为详细的参考答案,请扫描右边的二维码,关注编辑部的官微“高中数学解题反思”,不但能获悉详细参考答案,还可以另辟蹊径,开拓知识视野,学会解题反思!

(责任编辑 徐利杰)