导数、微积分知识结构与拓展

■郑州一中 潘莹慧

导数、微积分知识结构与拓展

■郑州一中 潘莹慧

一、知识结构框架

二、结构分析

函数是两个数集间的一种特殊对应,是两个变量间的变化规律,函数的导数和定积分是函数知识的提升,它们都是特殊类型的极限,极限是研究变量在无限变化中的变化趋势,本质是静止中认识运动,有限中认识无限,量变中认识质变,前者的对应是偏静态的,后者是偏动态的。而高中教材淡化了极限,从数形结合角度,结合曲线切割线斜率以及曲边梯形面积的实际背景,描述了这种动态的对应,这种处理,能使我们更清楚导数与积分的原始作用,理解微积分基本定理,确定导数与定积分为互逆运算,从而简化了麻烦的定义运算。从这个意义上讲,导数、微积分的考查内容,还是以工具性为主。对定义的理解是熟练运用导数求单调性、极值、最值,以及利用积分求面积的前提。

三、实例分析

例 1 (1)若f'(x0)=2,求

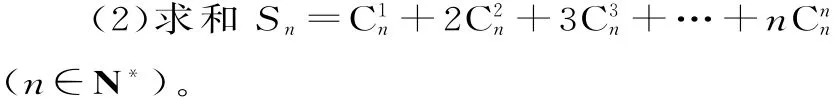
分析:(1)导数定义。(2)合理运用逆向思维。由求导公式(xn)'=n xn-1,可联想到它们是另外一个和式的导数。关键要抓住数列通项的形式结构。

例2 已知f(x)=a x3+b x2+c x(a≠0)在x=±1时取得极值,且f(1)=-1。

(1)试求常数a、b、c的值;

(2)试判断x=±1时的值是函数的极小值还是极大值,并说明理由。

分析:利用一阶导数求函数的极大值和极小值的方法是导数在研究函数性质方面的继续,也是导数应用的关键知识点,通过对函数极值的判定,可加深对函数单调性与其导数关系的理解。考查函数f(x)是实数域上的可导函数,可先求导确定可能的极值,再通过极值点与导数的关系,建立由极值点x=±1所确定的相等关系式,运用待定系数法求值。

解:(1)f'(x)=3a x2+2b x+c,因为x=±1是函数f(x)的极值点,所以x=±1是方程f'(x)=0,即3a x2+2b x+c=0的两根。

当x＜-1或x＞1时,f'(x)＞0;当-1＜x＜1时,f'(x)＜0。所以函数f(x)在(-∞,-1)和(1,+∞)上是增函数,在(-1,1)上是减函数。

所以当x=-1时,函数取得极大值f(-1)=1;当x=1时,函数取得极小值f(1)=-1。

小结:本题难点是在求导之后,不会应用f'(±1)=0的隐含条件,因而造成了解决问题的思维障碍。

例3 求下列各曲线围成的平面区域的面积:

(2)y=x-2,x=y2。

分析:用定积分计算平面区域的面积,首先,确定已知曲线围成的区域;其次,由区域

小结:(1)如果函数f(x)在点x=x0的一个δ区域:(x0-δ,x0+δ)内有定义,对任意的x∈(x0-δ,x0)∪(x0,x0+δ)总有f(x)＜f(x0)(f(x)＞f(x0)),则称f(x0)为函数f(x)的极大(小)值,x0称为极大(小)值点。

(2)注意极值与最值的区别,极值是相对于领域而言,它仅是极值点附近的局部范围内的相对大小,而最值是相对于闭区间而言,它是函数在给定的闭区间上的全部函数值中最大(小)的值。

(责任编辑 刘钟华)