搭建教学“脚手架”开辟学习“新天地”

◇陈 云

搭建教学“脚手架”开辟学习“新天地”

◇陈 云

学生学习的过程是通过活动参与来实现知识内化的过程。在这个过程中，学生对于所要解决的问题与已有的知识、经验之间，可能存在这样或那样的差异，教师需要为学生提供学习的“脚手架”，引导、帮助学生消除差异，从而完成学生所不能独立完成的活动；为学生创设足够宽松的环境，让学习者之间互相提供支持和帮助，互为“脚手架”，从而将知识内化为技能。

那么，作为“脚手架”的搭建者，教师必须思考：“脚手架”需要搭在何时、建在何处？笔者认为这个“脚手架”的特点应当为“三个能够”：能够让复杂的“知识线”逐渐明朗、统一；能够激发学生在“概念框架”内自由地继续攀升；能够方便把管理学习的任务逐渐由教师转移给学生。

一、在知识最近发展区落“脚”

搭建“脚手架”应落“脚”于知识的最近发展区。我们常听到老师在新课伊始提出“关于这些内容，你已经知道了什么”“通过预习，你学会了什么”等问题，目的都是在寻找学生的认知起点，确定学生已有知识与所要解决问题之间的差异，从而准确找到搭建“脚手架”的“落脚点”。

如北师大版教材四年级下册第三单元 “小数乘法”第三课时“街心广场”的内容，教材沿用前两课时的方法，借助单位转换、面积模型，探索简单的小数乘法的计算方法，从而发现积的小数位数与乘数小数位数之间的关系。在这一单元的第一课时“买文具”一课中，学生已经学习了简单的小数乘整数，本课时是对前一知识点的延伸和发展。因此，在课前预习的“导学案”中，我为学生搭建了以下的“脚手架”。

1.回顾“买文具”一课的学习过程，找到与本节课在学习内容和学习方法上的异同。

2.结合面积模型，你能否从小数意义的角度解释 0.3×0.2＝0.06？

3.完成下列表格。

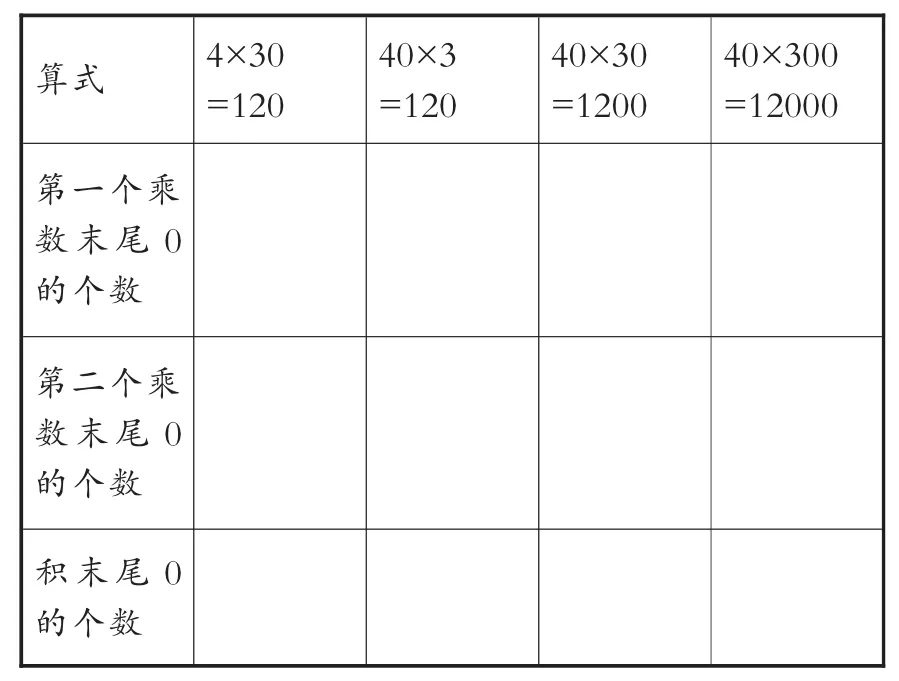
算式 4×30＝120 40×3＝120 40×30＝1200 40×300＝12000第一个乘数末尾0的个数第二个乘数末尾0的个数积末尾0的个数

4.尝试填写本课时第4个问题的表格（如下表），思考你有什么发现。

种种记载，足见绝非正经医者的所谓“术士”所炼的丹药，实在是凶险之物。那么，这些掌握了当时社会中最高权力和文化资源的人们，为什么会前赴后继地去吃它呢？原因很简单，那些炼丹的术士，无一不宣称自己所炼的是“长生不老药”。

积的小数位数与乘数的小数位数有什么关系？算一算，想一想。

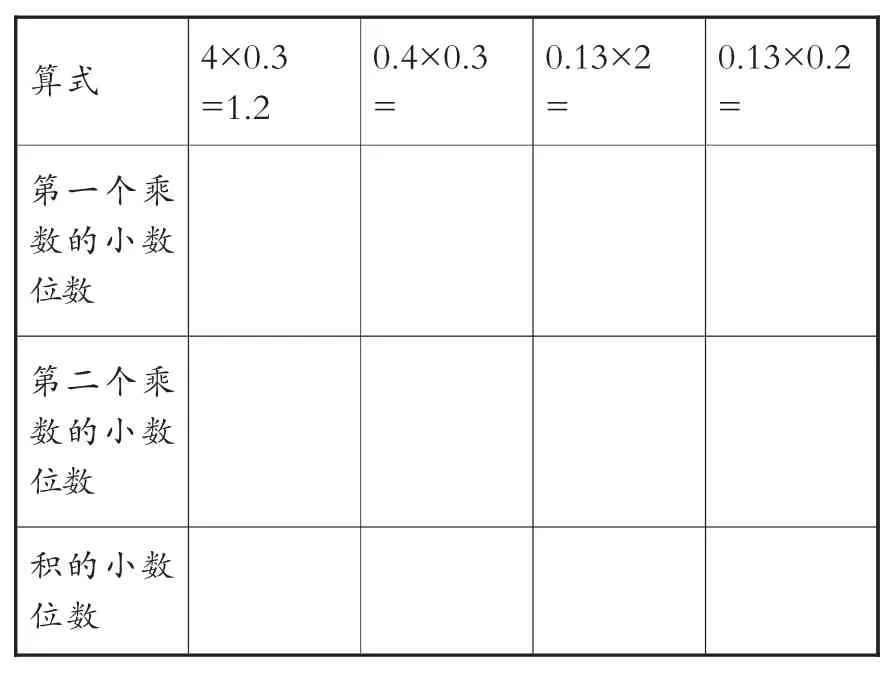
算式 4×0.3=1.2 0.4×0.3=0.13×2=0.13×0.2=第一个乘数的小数位数第二个乘数的小数位数积的小数位数

这样的“脚手架”在学生的知识最近发展区落“脚”，让复杂的知识线明朗、统一，学生可以借助这个“脚手架”，找到新旧知识间实质性的联系，使认知结构上下贯通，从而能够顺利开展对新知识的自主研究和探索。

二、在认知冲突处搭“手”

搭建“脚手架”应搭“手”在认知冲突处。在搭“手”的过程中，起初的引导、帮助可以多一些，以后逐渐减少，放手让学习者之间互相提供支持和帮助，互为“脚手架”。特别是，当学生对某一问题产生不同看法时，创造一个“原生态”的、促使思维碰撞的“脚手架”，让学生抓住“脚手架”中的概念框架继续攀升，最终必将在这个知识点的学习过程中烙上属于他们自己的个性化体验。

如在北师大版教材五年级上册“分数的再认识（二）——分饼”的教学中，教材给出了这样一幅情境图（如图 1）。

图1

在学生动手分一分后，认知可能会发生很大冲突，主要有以下几种：

2.各组队员共同商讨，拿出证明观点正确的有效证据，并找到反驳他组答案的理由。

3.自由辩论，找到各组的联系和区别。

在这个完全开放的“脚手架”的支撑下，学生的表现异常精彩。

图2

乙组拿起5张圆纸片叠在一起用剪刀剪，动态呈现了“把这些饼平均分成4份，取其中1份”的过程，每人分得

丙组也拿出5张纸片，找来4位同学实际分一分。首先每人分“一张饼”，再把剩下的平均分成4份，每人得到张，共分得

同时，丙组的学生不甘示弱：4个人分5张饼，每人得到的肯定要多于1张饼，为什么会是一个小于1的分数呢？

……

三、在思维延伸处立“架”

教学不仅要把“脚手架”搭建在学习者的“过去”与“今天”之间，更应延伸至“明天”，其实质是通过搭建“脚手架”，引领学生把感性认识理性化、模糊认识清晰化、问题讨论主题化，最终把管理学习的任务逐渐由教师转移给学生自己，直至撤去“脚手架”。

如在学习“乘法交换律”时，我给学生搭建了这样的“脚手架”：

1.回顾你是怎样发现和运用“加法交换律”的，现在你又想到了什么？（让学生自己想到：其他运算有没有交换律）

2.在小组内开展自主探究，填写下表。

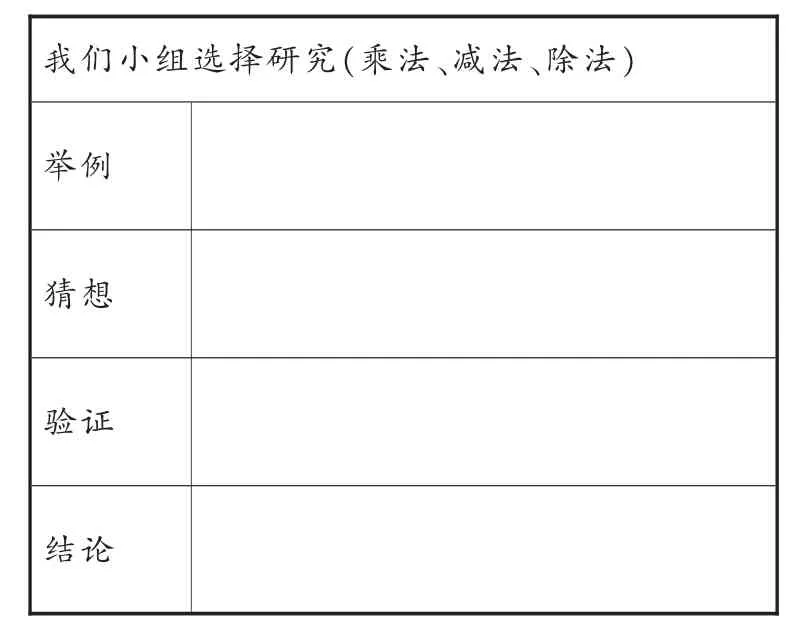
我们小组选择研究（乘法、减法、除法）举例猜想验证结论

3.反思小组研究过程，填写自主学习评价表。

我的收获我在小组中的贡献同伴对我的评价我的反思

之所以把学习的过程完全交给学生，是因为在“乘法交换律”学习之前，学生已经有大量的感性认识，并且能运用交换乘数的位置来验算乘法，而乘法交换律与加法交换律有着同样的思想方法，教师完全可以有目的地先扶后放，少扶多放，促使学生思维产生跳跃、延伸，自主完成学习。

这个过程中，对于新知（乘法交换律）的学习任务，老师成功地将其转移给了学生，并最终撤去“脚手架”，学生在自主的学习探索中最终完成个人的自我评价和学习小组对个人的学习评价，实现全面发展。

（作者单位：安徽怀宁县振宁学校）