基于预应力杆的空间桁架天线固有频率调节技术

谢兰川，明路遥，吴永鹏，张云，杨九州

基于预应力杆的空间桁架天线固有频率调节技术

谢兰川，明路遥，吴永鹏，张云，杨九州

（西南技术工程研究所，重庆 400039）

研究预应力杆对大型空间桁架天线固有频率影响，提出采用作动器实时对在轨空间天线低阶固有频率进行调整，主动避免共振现象发生。针对大型空间桁架天线结构有限元模型，采用降温法对桁架杆施加预应力，重点分析预应力大小、预应力杆位置、预应力杆数量对整体结构固有频率的影响。增加预应力大小、合理布置预应力杆位置、增加预应力杆数量能够增加空间桁架天线固有频率的改变率。合理优化空间桁架天线上预应力杆，可实现对在轨运行的空间桁架天线低阶固有频率实时调整，可为空间桁架天线避振设计提供参考。

桁架天线；固有频率；预应力

在信息技术高度发展的今天，空间卫星在通信、观测、空间科学等领域，尤其是军事领域发挥着日趋重要的作用[1-2]。其中空间桁架天线在卫星实现通信、观测等功能上具有决定性作用。空间可展开桁架天线作为一种新型特殊的空间结构具有净空间值高、在空间容易展开或装配、受运载器载荷舱尺寸限制小等优点而得到广泛发展[3]。为了提高星载天线传递信号增益，扩大信号传输带宽，减小地面接收装置体积等，要求星载天线的尺寸越来越大，例如美国研发的第五代电子侦察卫星的空间可展开桁天线甚至发展到了150 m左右[4-5]。大型空间桁架天线具有结构柔度大、内阻小等结构特点，但其在轨运行所处的太空环境载荷非常复杂。卫星作动、姿态调整、动量轮、陀螺等各种因素都可形成低周扰动，激发空间天线的共振响应[6]，对卫星天线的运行与结构安全造成极大威胁[7]。空间天线尺寸的大型化已使其在在轨运行时的共振现象愈加严重，必须对空间桁架天线进行共振抑制问题的研究。

国内外关于空间柔性桁架天线结构共振抑制问题早有研究[8]。西安交通大学与空间技术研究院西安分院研发的双压电堆预应力调节装置，利用天线振动方向作相反运动来抑制共振。这种方法控制系统复杂且非常耗能，较难投入使用。师甜等[9]对比分析了斜支杆对环形天线第一阶频率的影响，当第一阶频率改变率达到20%时能达到良好避振效果。师甜等[10]对斜支杆进行轴向、垂直于轴向加载预应力的方式找出了一个满足要求的加载方向，但对于在轨运行的大型空间展天线，这种方式不便于实现工程应用。

文中提出利用作动器对桁架杆产生预应力来改变天线结构固有频率，错开共振激励频率，从而达到避免共振的目的。建立了大型空间桁架的有限元模型，推导了预应力对空间桁架天线结构固有频率影响的基本公式。以数值模拟的方式着重分析了预应力杆位置和数量、预应力大小等因素对天线结构固有频率调整效果的影响。提出了大型桁架天线主动避免共振响应的实用方法，切实为工程实际中天线避振设计提供参考。

1 预应力杆结构固有频率

在自主控制作用下，激振力频率处于系统带宽之外时，共振响应能够得到有效抑制[9]。轴向作动器是空间桁架天线上的动力学调节机构，它产生的轴向力与轴向位移能方便地实现在轨主动控制。因此空间桁架天线设计时可在周边桁架杆中嵌入作动器，通过电能使作动器产生轴向力给桁架杆施加预应力，改变天线结构刚度从而改变结构固有频率，使外界激振频率处于系统带宽之外，避免共振响应发生。

1.1 预应力杆结构单元的刚度矩阵

杆单元示意如图1所示。

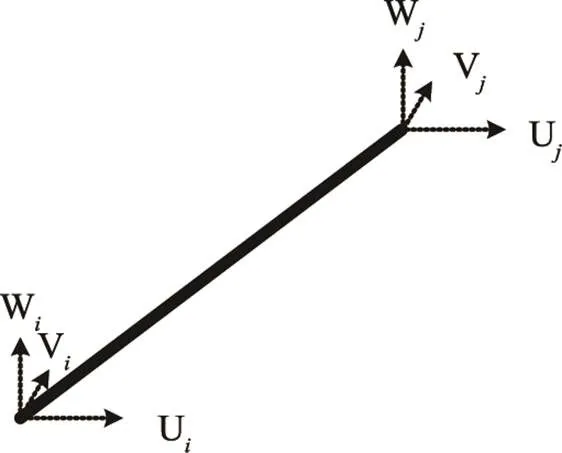
图1 杆单元示意

杆单元节点在整体坐标系中的位移向量与相应的节点力向量为：

在轴向预应力0作用下，杆单元平衡方程为：

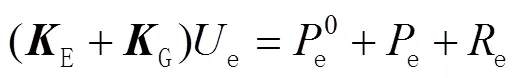
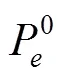
E和G的具体表达式为[12]：

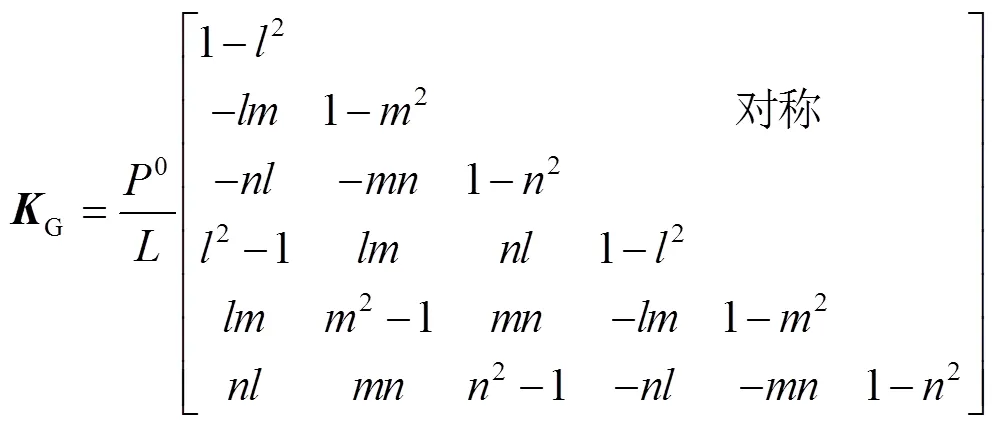
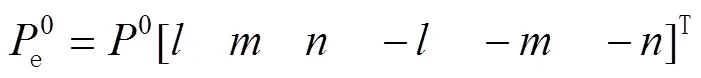
式中：=cos，=cos，=cos分别为杆单元对于整体坐标系方向余弦。预应力杆单元的等效刚度矩阵为：

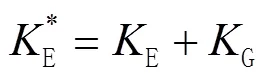
1.2 预应力结构固有频率

多质点弹性体系的无阻尼自由振动方程为[13]：

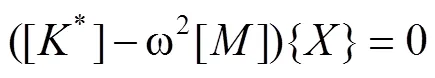
式中：[*]为预应力结构刚度矩阵；[]为结构质量矩阵；{}为振动模态；为振动圆频率。自由振动时结构各点振幅{}不全为0，则矩阵行列式必然为0。结构自由振动频率特征方程为：

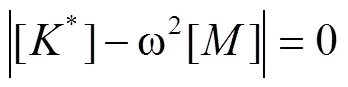
预应力结构的固有频率为：

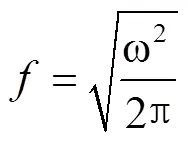
2 空间桁架天线有限元模型与降温法

在ANSYS中建立复环桁架天线模型，主要包括周边桁架、索网和伸展臂等。复环内、外径分别为9，10 m，展开高度为2.2 m，支撑臂长5 m。索网、杆件和伸展臂分别由索单元LINK180、杆单元LINK180与梁单元BEAM188建立，节点质量由MASS21单元模拟，如图2所示。空间桁架天线的前四阶模态振型与振动频率如图3所示。

文中在ANSYS中使用降温法对桁架杆单元施加预应力，实现对有限元模型预应力的施加。降温法的原理是通过对杆单元实施温降实现预应力的施加，即为杆单元设定一个初始温度，并且给定一个温降值，使得杆单元产生一个收缩变形，此初始应变将使杆单元产生预拉力作用，力的大小为所要达到的预应力数值。温降值按式(11)计算[14]：

图2 桁架天线结构有限元模型

图3 前四阶模态振型与振动频率

式中：Δ为施加的降温值；为预拉力值；为杆截面面积；材料弹性摸量；为材料膨胀系数。

3 预应力杆影响结构固有频率机理分析

采用降温法分别对单根杆或多根组合杆施加预应力，分析不同预应力杆位置、预应力大小、预应力杆数量等因素对空间桁架天线结构频率的影响。将所有复环桁架与斜支杆进行编号，共202根。取近臂端的斜支杆、左侧和远端处杆件作为预应力施加位置，如图4所示。

3.1 预应力杆位置

分别在斜支杆、左端与远端的单根杆中施加1000 N的预拉力，得结构前四阶频率的改变率，见表1。

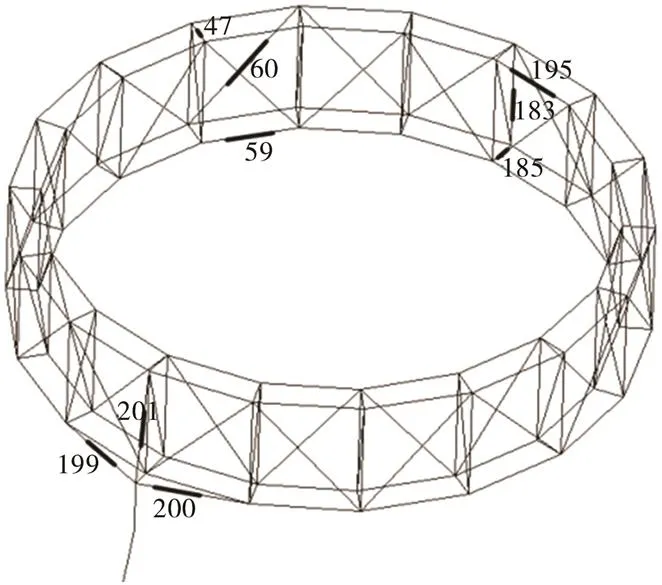
图4 预应力杆位置分布

表1 不同位置的预应力杆引起结构频率改变率 %

对第一阶固有频率伸展臂较其他位置影响更大，固有频率改变率达24.92%>20%，即能达到共振抑制的效果。每个方位都存在对第一阶频率影响较大的杆，如右侧的杆59与远端的杆195，改变率分别达到21.86%和21.87%。对称位置的杆，如杆199与杆200，对结构固有频率的影响相同。

从振型上看，当杆轴线方向与振动方向一致时，此杆对固有频率影响较大。因此，杆中的预应力会使其结构在杆轴线方向的刚度改变，进而改变结构固有频率。例如，杆199，200，59，195上的预拉力在第一阶摇头模态振动方向上的分量大，杆183上的预拉力在第一阶摇头模态振动方向上的分量小。

3.2 预应力大小

应用于振动控制的作动器包括压电陶瓷作动器、压电薄膜作动器、电致伸缩作动器、磁致伸缩作动器、形状记忆合金作动器和电流变流体作动器等。新型的作动器具有大位移、大驱动力、体积小等特点[15-16]。航天结构设计中则需根据体积、驱动力范围、安装方式等因素选择合适的作动器对结构施加预应力。现取杆59，对其施加不同数值预应力，天线整体结构各阶固有频率的改变率见表2。

表2 同一杆件中不同预应力对天线结构频率改变率 %

预应力杆中的预拉力使结构固有频率增加，预压力使得结构固有频率减小。随着预应力绝对值的增加，结构频率改变率增加。数值相等的预拉力与预压力对结构频率改变率大致相同。

3.3 预应力杆数量

分别取数量从1到4的预应力杆，每杆均施加1000 N预拉力，得到对结构前四阶频率的改变率见表3。

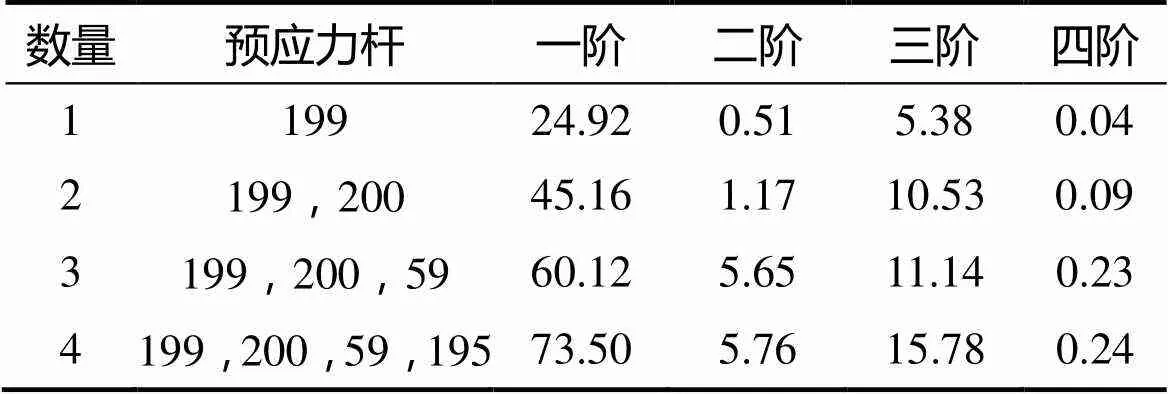
表3 不同数量的预应力杆件对天线频率改变率 %

由表3可知，增加预应力杆的布置数量能有效增加对结构固有频率的改变率，但多根杆的效果略小于单根杆的线性叠加。随着固有频率阶次的增加，频率改变率逐渐减小，因此对高阶频率的调整将更加困难，需要更大的预应力或者在更多位置布置预应力杆。

3 结语

基于预应力改变结构刚度的原理，提出了在大型空间桁架天线中布置预应力杆，主动调整结构固有频率，达到避免共振响应的目的。着重分析了预应力杆的位置和数量、预应力大小等因素对天线结构的低阶固有频率的影响。合理优化空间桁架天线上预应力杆，可实现对在轨运行的空间桁架天线低阶固有频率实时调整。文中的方法与分析可为空间桁架天线结构设计提供参考。

[1] 李刚. 空间可展天线结构的设计分析与索膜结构分析[D]. 杭州: 浙江大学, 2004.

[2] 江芳龙. 大型星载天线的模态局部化问题研究[D]. 哈尔滨:哈尔滨工业大学, 2010.

[3] 章令晖, 李甲申, 王琦洁, 等. 航天器用复合材料桁架结构研究进展[J]. 纤维复合材料, 2013, 62(4): 62-68.

[4] 梅国宝, 吴世龙. 电子侦察卫星的发展､应用及其面临的挑战[J]. 舰船电子抗, 2005, 28(4): 28-31.

[5] 冯如. 美国电子侦察卫星的发展概况[J]. 国际太空, 2000(10): 6-8.

[6] 杨新峰, 白照广, 杨栋, 等. 动量轮诱导的卫星地面微振动特性研究以及在轨仿真分析[J]. 装备环境工程, 2015, 12(3): 15-22.

[7] 王其政, 刘斌. 宇航爆脱冲击事故与环境问题[J]. 强度与环境, 1993(3): 23-28.

[8] 牟全臣, 黄文虎, 郑钢铁, 等. 航天结构主、被动一体化振动控制技术的研究现状和进展[J]. 应用力学学报, 2001, 18(3): 1-7.

[9] 师甜, 肖勇. 一种大型可展开天线结构频率调整技术研究[J]. 现代电子技术, 2013, 36(11): 75-78.

[10] 师甜, 肖勇, 于新战. 关键部件刚度对环形可展开天线频率影响研究[J].电子设计工程, 2013, 22(21): 59-61.

[11] 高军虎. 展开天线结构动力学和振动控制分析[M]. 杭州: 浙江大学出版社, 2012.

[12] 孔新国, 吕令毅. 索结构预应力、几何非线性和刚度关系的研究[J]. 工业建筑, 2002, 32(2): 49-50.

[13] 刘晶波, 杜修力. 结构动力学[M]. 北京: 机械工业出版社, 2005.

[14] 何琳, 王家林. 模拟有效预应力的等效荷载-实体力筋降温法[J]. 公路交通科技, 2015, 32(11): 75-80

[15] 李响, 朱海军, 雷林. 一种大位移微型作动器及其驱动方法: 中国专利, 106487272[P]. 2017-03-08.

[16] 马国亮, 徐明龙, 陈杰, 等. 一种磁_压电双向步进式大位移作动器及其作动方法: 中国, 105391334[P]. 2016-03-09.

Natural Frequency Adjustment Technique of Space Truss Antenna Based on Prestressed Bar

XIE Lan-chuan, MING Lu-yao, WU Yong-peng, ZHANG Yun, YANG Jiu-zhou

(Southwest Technology and Engineering Research Institute, Chongqing 400039, China)

To study influences of prestressed bar on natural frequency of large space truss antenna and propose to adjust natural frequency of a orbiting antenna to avoid resonance.The finite element model of large space truss antenna was presented and the cooling method was used to apply prestress to the truss bar. The influences of the size of prestressing force, the position of prestressed bar and the number of prestressed bars on the natural frequency of the whole structure were analyzed emphatically.Increasing the magnitude of prestress, arranging position of prestressed bars reasonably and increasing the number of prestressed bars could increase the change rate of natural frequencies of space truss antennas.Reasonable optimization of prestressed bar on space truss antenna can realize real-time adjustment of low order natural frequency of space truss antenna in orbit, which can provide reference for avoidance of vibration in design of space truss antenna .

truss antenna; natural frequency; prestress

10.7643/ issn.1672-9242.2017.11.016

TJ07；TG174

A

1672-9242(2017)11-0081-04

2017-06-07；

2017-07-01

谢兰川（1987—），男，硕士，主要研究方向为结构振动与控制。